Bag of Words

Bag-of-Words Representation

1. dictionary에 등록하고 중복 제거

• 예시 문장 : "John really really loves this movie" / "Jane really likes this song"
• dictionary : {"John", "really", "loves", "this", "movie", "Jane", "likes", "song"}
• 두 개의 문장에서 "this"라는 단어가 중복으로 등장하였으나, dictionary에는 하나만 등록

2. Unique word들을 one-hot vector로 Encoding

• dictionary에 있는 단어들에 모두 one-hot vector 적용
  
• 단어 개수를 차원으로 적용하고, 해당 dimension의 값만 1로 처리. 나머지는 0
• distance는 $\sqrt2$
• one-hot vector를 이용함으로써 차원의 함축을 나타내기 때문에 cosine similarity는 0
• 단어의 의미와 상관 없이 모두가 동일한 관계를 가진 형태로 단어의 vector 표현형 결정

3. 문장/문서는 one-hot vector들의 합으로 나타낼 수 있음

• 모두 동일한 차원의 vector를 가지고 있기 때문에 가능
• 문장 1 : "John really really loves this movie"
  - John + really + really + loves + this + movie = [1 2 1 1 1 0 0 0]
• 문장 2 : "Jane really likes this song"
  - Jane + really + likes + this + song = [0 1 0 1 0 1 1 1]
  

NaiveBayes Classifier for Document Classification

Bag-of-Words for Document Classification

• Bag-of-Words vector로 나타낸 문서를 정해진 category, 혹은 class 중에 하나로 분류할 수 있는 대표적 방법.
  

Bayes' Rule Applied to Documents and Classes

• 아래 식에서 d는 문서, c는 class
  
• 문서 d는 연속된 단어들 w와 class c를 포함하고 있음
• 문서의 확률은 각 단어가 나타날 확률을 곱하여 나타낼 수 있음
• 특정 category(class) c가 고정이 되었을 때 문서 d가 나타날 확률을 $P(d|c)$, c는 독립 사건, w는 모두 동시 사건 d에 의해 발생
• $P(d|c)P(c) = P(w_1, w_2, ..., w_n|c)P(c)$ → $\prod_{w_i\in W}P(w_i|c)$

• 예시
  

• 각각의 class가 가지는 확률값은 $P(c_{CV}) = \frac{2}{4} = \frac{1}{2}$, $P(c_{NLP}) = \frac{2}{4} = \frac{1}{2}$

  • 각 단어 $w_i$에 대해 class c에 대한 conditional probability 구할 수 있음
  • $P(w_k|c_i) = \frac{n_k}{n}$에서 문서의 topic이 $c_k$이면서 상황이 $w_k$일 때를 $n_k$
    
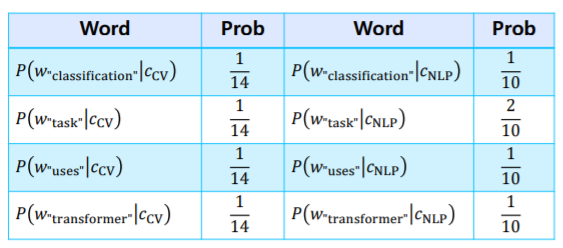
  • $\frac{대상이\space되는\space문서에서\space내가\space찾으려는\space단어\space개수}{총\space단어\space개수}$이므로 중복 제거 X

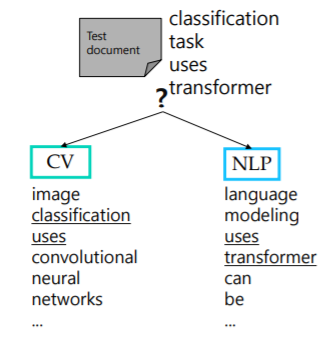
• 예시의 test document $d_5$에서 transformer를 사용하였을 경우

  • 각 class에 대한 conditional probability 계산
  • 해당 문서에서 highest probability를 가지는 class를 선택
  • $P(c_{CV}|d_5) \newline= P(c_{CV})\prod_{w\in W}P(w|c_{CV})\newline= \frac{1}{2}\times\frac{1}{14}\times\frac{1}{14}\times\frac{1}{14}\times\frac{1}{14} = 0.00005$
  • $P(c_{NLP}|d_5) \newline= P(c_{NLP})\prod_{w\in W}P(w|c_{CV})\newline= \frac{1}{2}\times\frac{1}{10}\times\frac{1}{10}\times\frac{1}{10}\times\frac{1}{10} \approx 0.00005$