B-tree / B+tree

Psj·2025년 3월 7일

F-lab

목록 보기

2/4

B-tree 동영상 설명

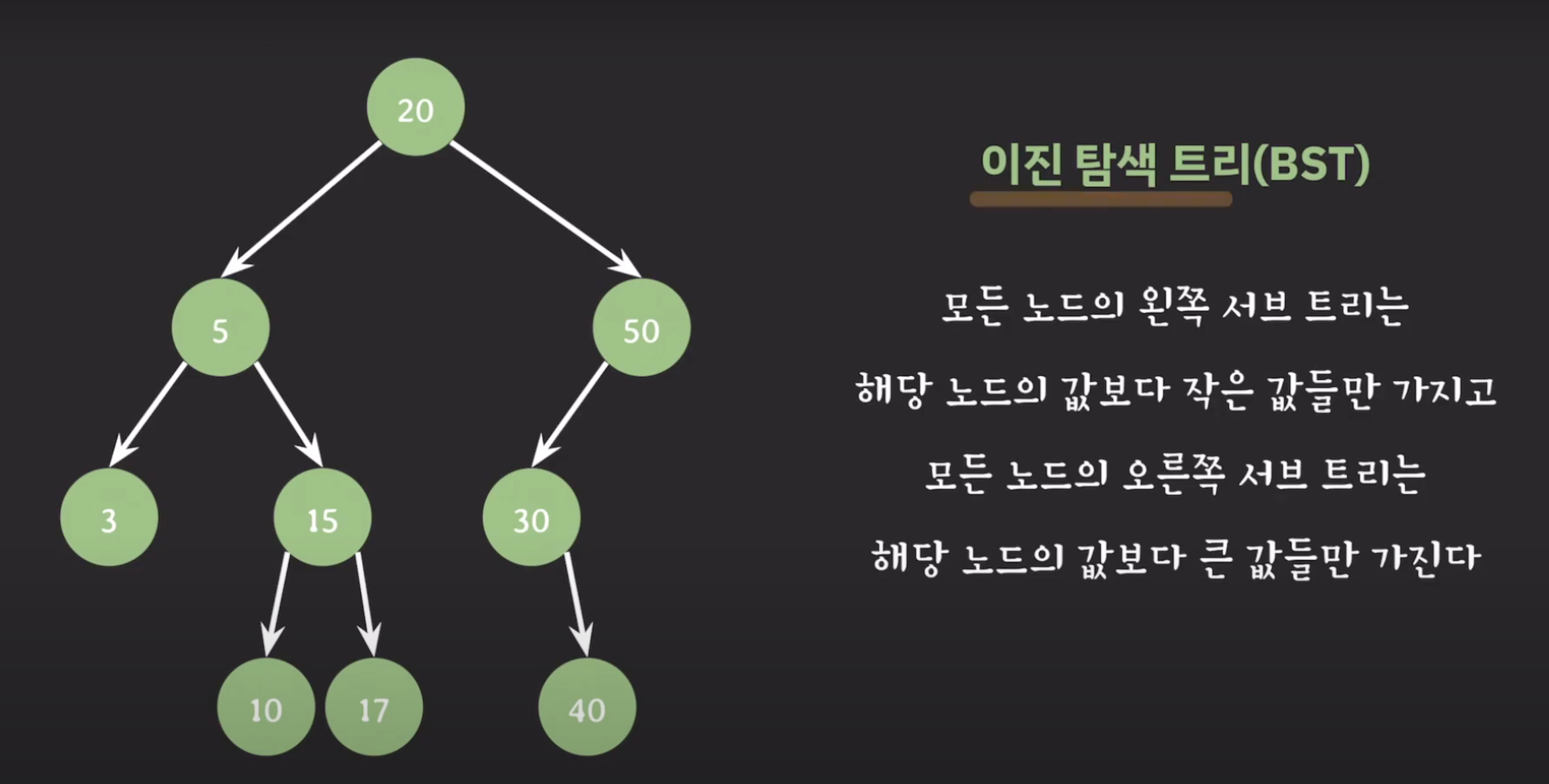
이진 탐색 트리는 자녀노드는 최대 두개까지 가지는 특성을 가지는데
부모노드를 기준으로 왼쪽자식노드는 작은값, 오른쪽자식노드는 큰값들만 가진다.

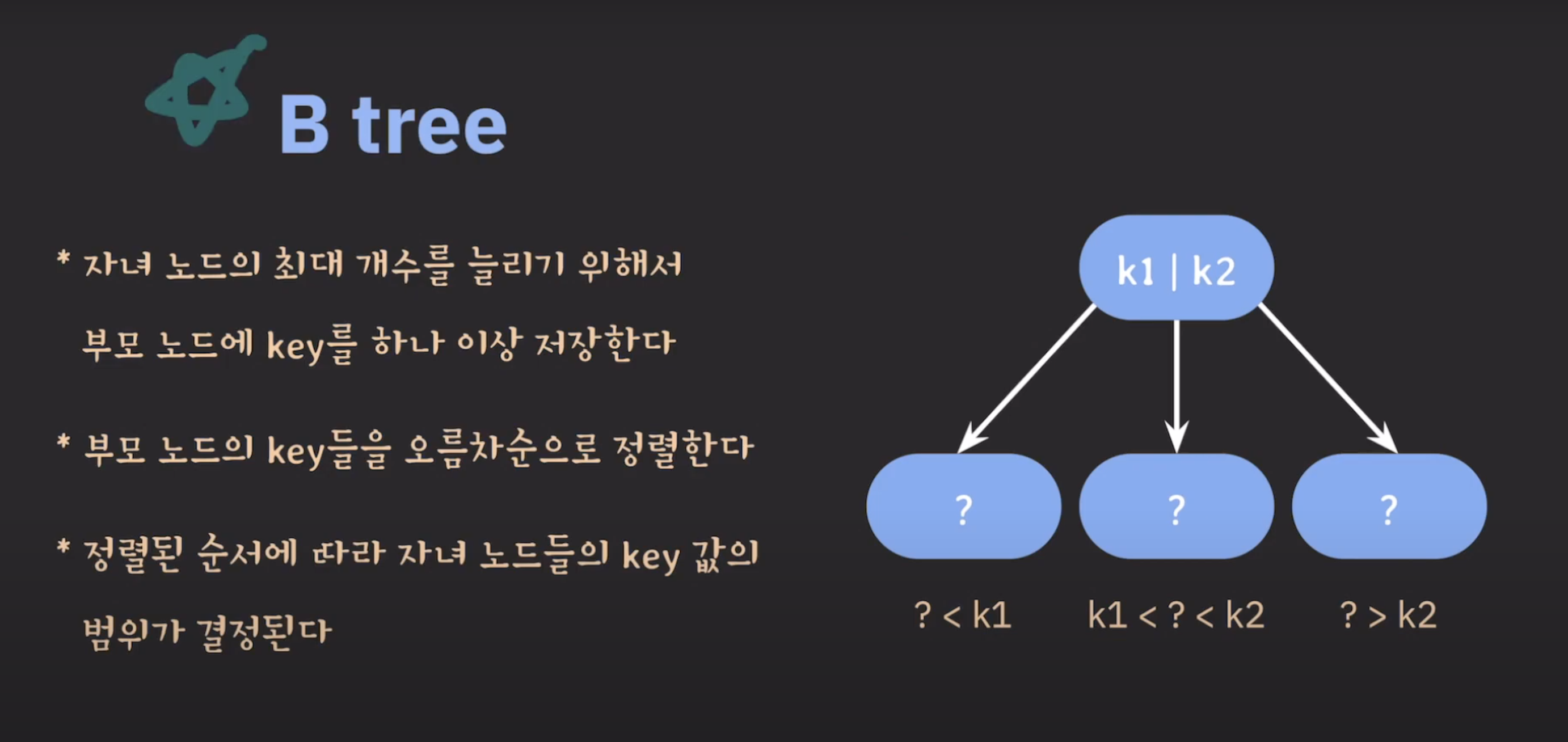
B tree 이다.
이런 방식을 사용하면 자녀 노드의 최대 개수를 입맛에 맞게 결정해서 쓸 수 있다.
최대 몇 개의 자녀 노드를 가질 것인지가 B tree를 사용할 때 중요한 파라미터이다.

최대 몇 개의 자녀 노드를 가질 것인지가를 M 이라고하고 M=3 이면 3차 B tree 라고 한다.
M 이 정해지면 나머지 파라미터들을 전부 계산 가능하다.

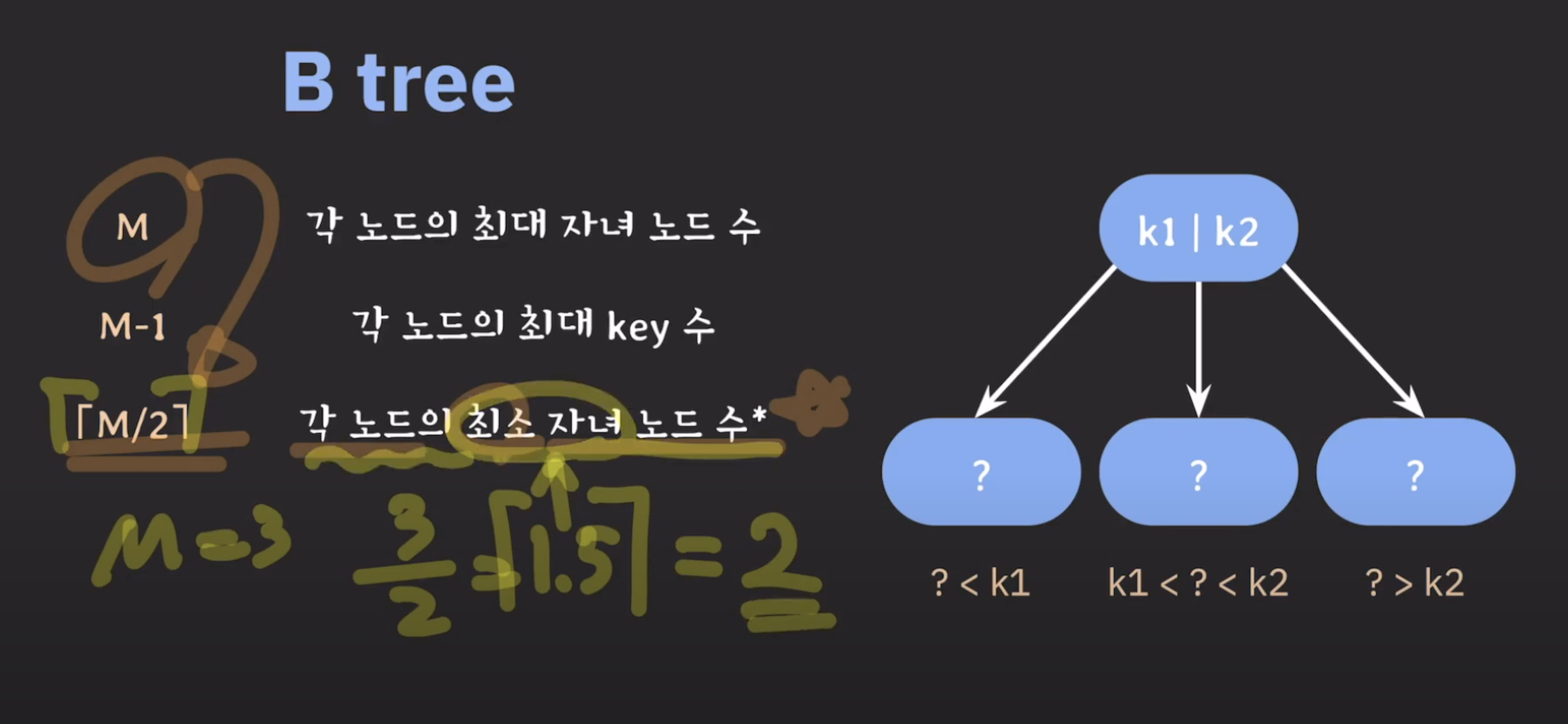
[M/2] 에서 [ ] 이 중괄호는 나눈값을 올림하라는 뜻이다.

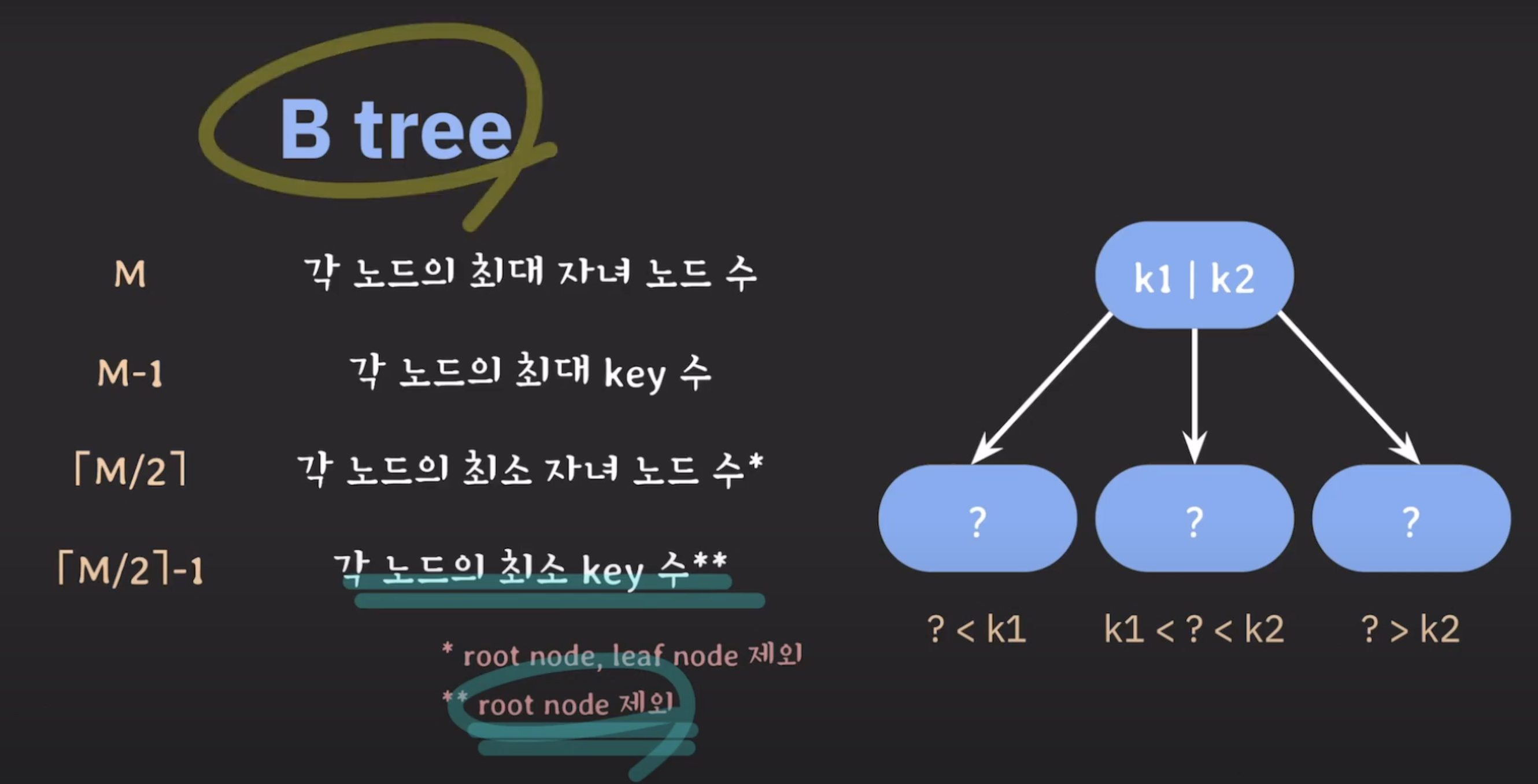
[M/2] 조건은 root node(출발점이 되는 노드), leaf node(자녀노드가 없는 노드)에서는 제외한다.
[M/2]-1 조건은 root node는 제외한다.

B tree 삽입 17:00부터 시청

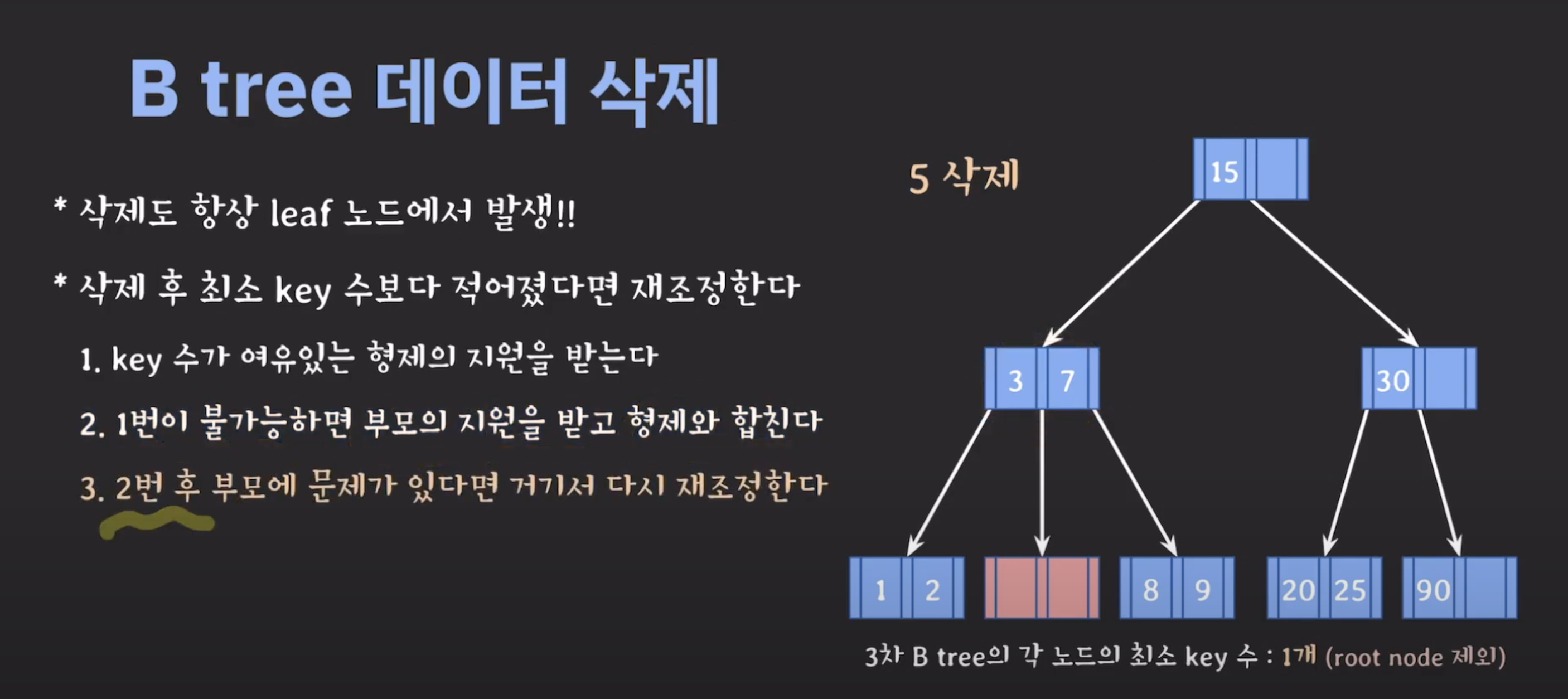
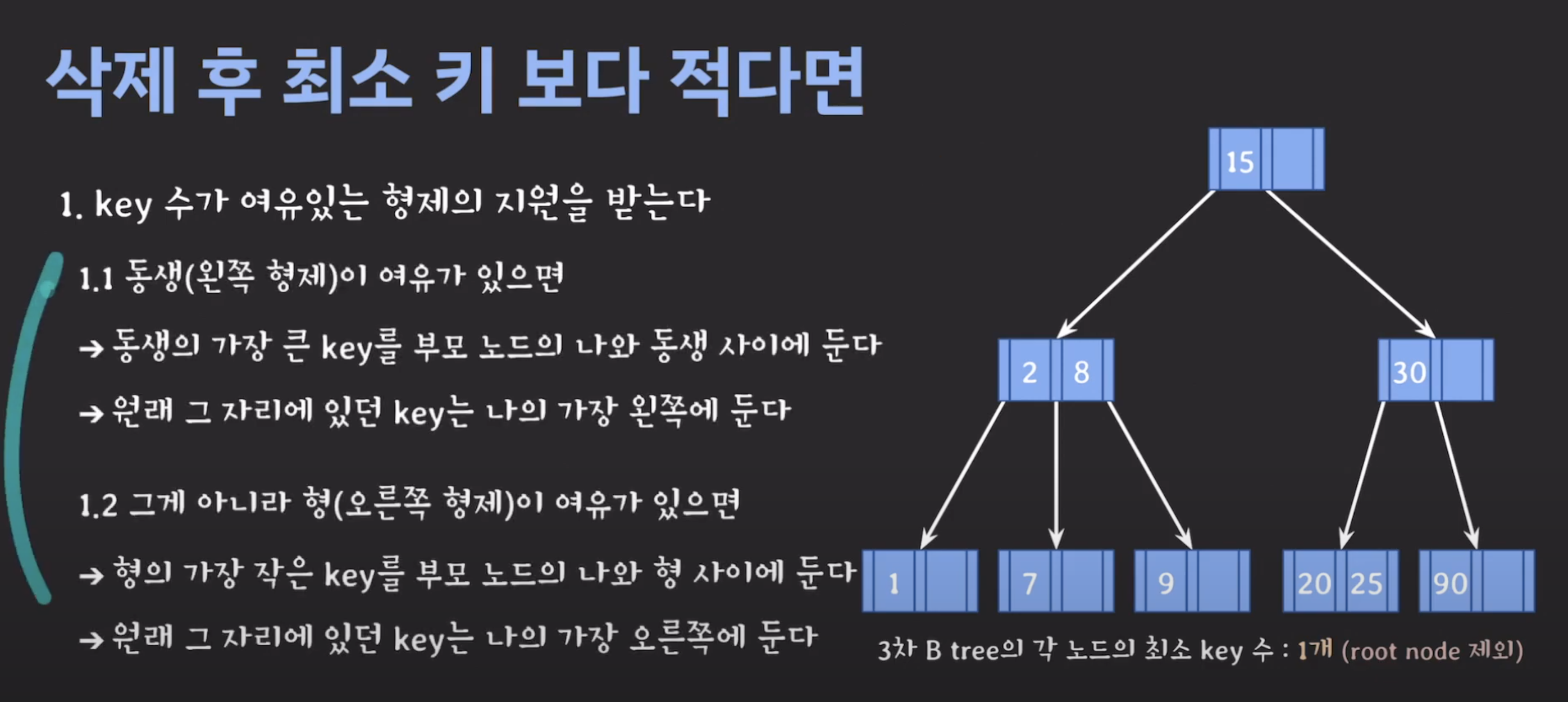
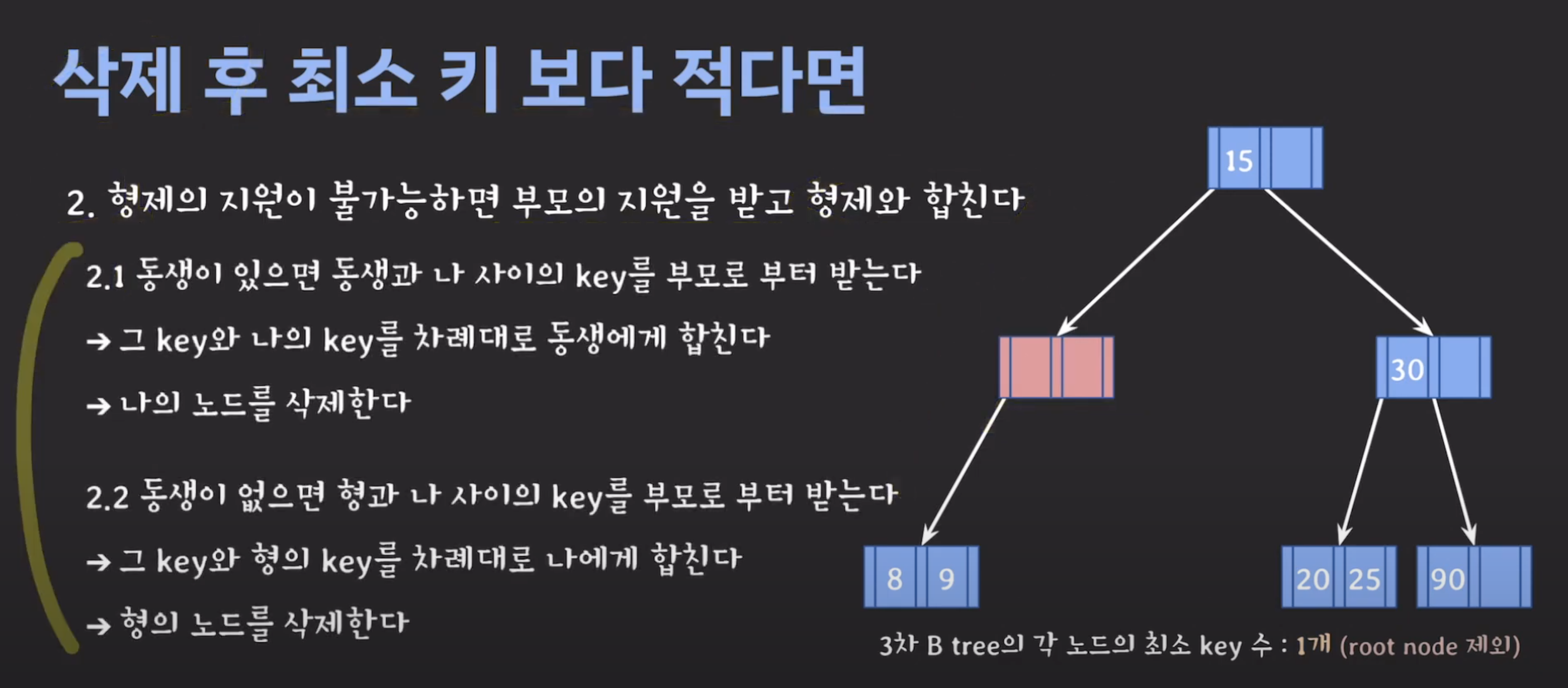
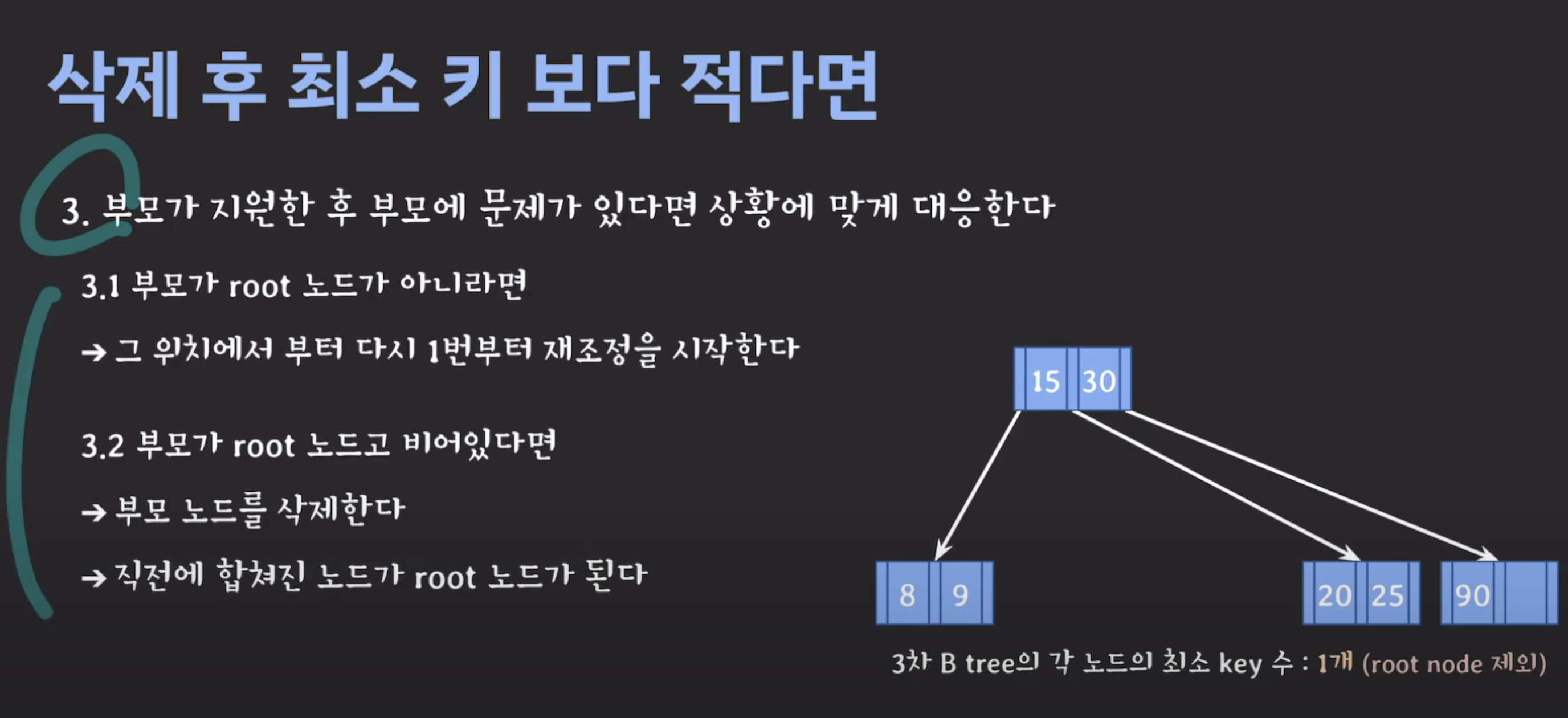
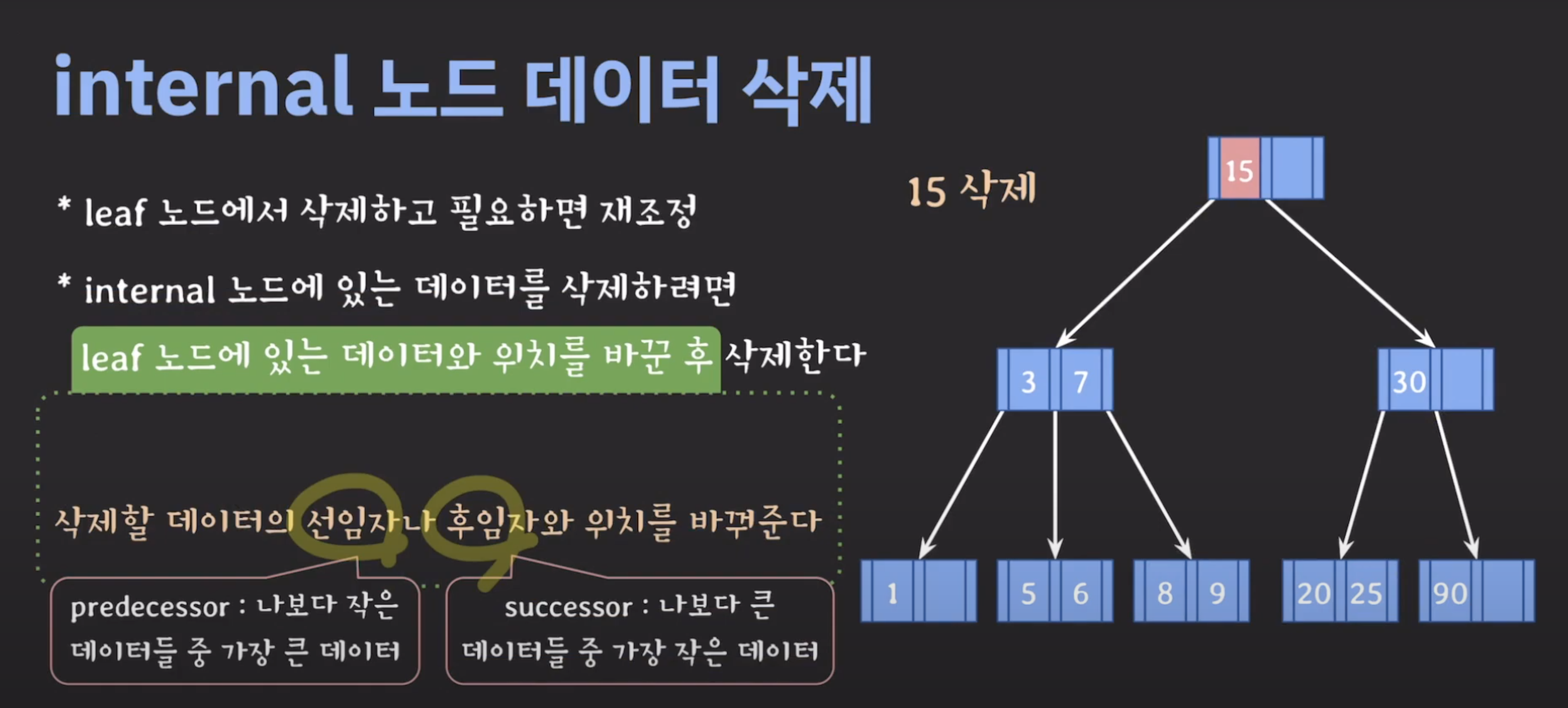
B-tree 설명

B-tree 설명 블로그

B+tree 설명

B+tree 설명 블로그

데이터베이스 인덱스는 왜 'B-Tree'를 선택하였는가

B트리를 이해하기 전에 먼저 디스크 구조부터 이해하자.

디스크 관련 내용 참조 강의 : https://www.youtube.com/watch?v=aZjYr87r1b8&ab_channel=AbdulBari

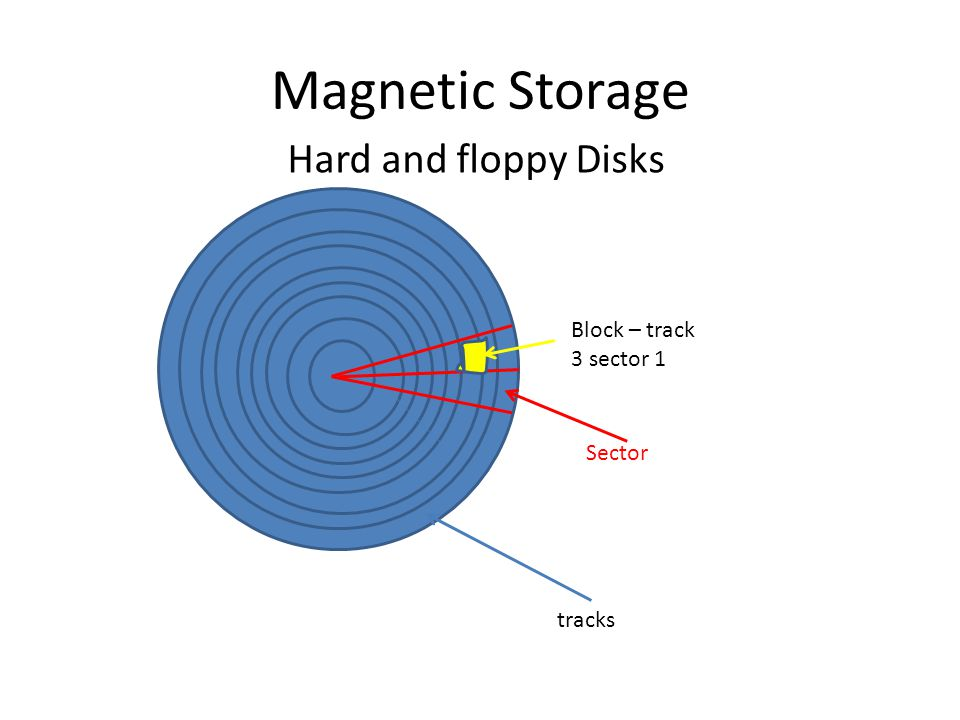
디스크는 섹터와 트랙으로 나뉘어져있음.
섹터는 디스크 영역을 파이처럼 나눔.
트랙(레벨)은 디스크의 깊이.
블럭은 특정 트랙의 섹터
블럭이 512 바이트로 이루어져있다고 하면, 0부터 511까지 1바이트씩 이루어져있는데, 1바이트는 각자의 주소를 가지고있다.(그걸 offset이라고 한다.)
디스크의 특정 지점을 읽으려면 섹터,블럭,offset을 알아야 한다.

데이터가 흐르는 과정 : 메인 메모리에서 프로그램을 돌리려면 데이터를 디스크에서 가져온다 → 결과가 나오면 그걸 디스크에 다시 담는다.

메인 메모리 내의 프로그램이 쓰는 데이터의 집합을 data structure라고 부른다. 데이터를 디스크에서 효율적으로 조직하는걸 DBMS라고 부른다.

예를들어 데이터베이스가 있고, Employee라는 테이블이 있다고 가정하자.

Employee

eid - 10byte
name - 50 byte
dept - 10byte
section - 8byte
add - 50 byte

총 128byte

(인덱스)pointer - 6byte 가정
데이터 베이스에는 100개의 record가 있는데, 1개의 record는 128byte라고 간주한다.
블록 1개가 512byte니까 1개의 블럭에 4개의 record를 넣을 수 있는 것이다. 디스크에 100개의 레코드를 넣으려면 총 25개의 블록이 필요하다.
이 데이터베이스에서 특정 데이터를 찾으려면 현재 상황으로는 25개의 블록을 하나씩 다 찾아봐야 한다. 운이 없으면 모든 블록을 다 탐색해야 한다.
그래서 빠른 탐색을 위해서 indexing을 해야 한다. index에는 eid와 pointer 가 존재한다. 각각의 pointer는 각각의 eid가 속한 레코드를 가리킨다.(레코드 포인터)
그러면 index는 어디에 저장되어있는가? index 또한 디스크에 저장되어있다. 단 데이터베이스와 따로 저장되어 있다. 100개의 인덱스를 저장하는데에는 4개의 블록이 필요하다.
(512byte/16(10byte+6byte(pointer) = 1블록에 32인덱스 저장가능)
100인덱스 / 32인덱스 = 3.125인데 3개이상의 블록이 필요하므로 4블록 필요
이제 데이터 탐색을 할 때 인덱스에 접근한다. 인덱스는 4개의 블록에 있으니까 4개의 블록을 탐색한다.
그리고 특정 인덱스에서 포인터를 찾아서 그 포인터가 속한 실제 데이터가 존재하는 블록으로 들어간다.
그러면 5개의 블록을 탐색하는거다.

멀티 인덱스

만약 레코드가 많아져서 1000개가 됐다고 생각해보자.
그럼 인덱스를 구성하는 블록의 개수는 32개(1000인덱스/32인덱스 = 32블록)로 많아진다. 인덱스 탐색의 효용이 작아진다.

그러면 어떻게 해야 하는가?

인덱스를 위한 인덱스를 만들면 된다. 한 개의 블록에 32개의 인덱스가 들어가니까,
인덱스 of 인덱스에서 1번째 인덱스는 1번째 블록에 들어갈 진입포인트, 2번째 인덱스는 2번째 블록에 들어갈 진입포인트... 등으로 구성한다.
인덱스 of 인덱스는 2개의 블록으로 구성된다.

실제테이블(Employee)

eid	name	dept	section	add
1	park	development	ddd	seoul
...	...	...	...	...
32	...	...	...	...
...	...	...	...	...
100	...	...	...	...

1레코드는 = 128byte, 4레코드 = 512byte
1블록 = 512byte까지 저장가능

1블록 = 4레코드 저장가능
25블록 = 100레코드 저장가능

eid 인덱싱 테이블

eid	pointer
1	0x1234
...	...
100	...

1레코드 = 16byte, 32레코드 = 512byte
1블록 = 512byte까지 저장가능

1블록 = 32레코드 저장가능
100레코드 = 100/32 = 3.125블록이 필요한데 3개이상의 블록이 필요

즉 100개의 레코드를 eid로 인덱싱한 테이블은 3개 이상의 블록이 필요함

1000개의 레코드를 eid로 인덱싱하는것을 가정했을때

1000 레코드 / 32레코드 = 31.25 그러니 31개의 블록필요

즉 1000개의 레코드를 eid로 인덱싱한 테이블은 31개 이상의 블록이 필요함

이 가정을 한 이유는 데이터가 많아졌을때 문제때문이다.
처음 100개의 레코드를 인덱싱했을땐
3개 이상의 블록만 뒤져서 데이터를 찾으면 됐지만

1000개의 레코드를 인덱싱하니
31개 이상의 블록을 뒤져서 데이터를 찾아야하게 됐다.
31개 이상의 블록 또한 무작위로 섞여있을테니 이것을 다 뒤지지 않기 위해
이번엔 블록들을 다시한번 인덱싱을 해주는것이 멀티 레벨 인덱스(Multi-Level Indexing)이다.

멀티 레벨 인덱스(Multi-Level Indexing)

실제테이블(Employee)

eid	name	dept	section	add
1	park	development	ddd	seoul
...	...	...	...	...
1000	...	...	...	...

eid 인덱싱 테이블

eid	pointer
1	0x1234
...	...
1000	...

1000개 인덱싱테이블은 디스크내의 32개의 블록 필요

블록 인덱싱 테이블(레코드수 31개)

eid	pointer (해당 키가 속한 1단계 인덱스 블록)
1	블록 1 (1단계 인덱스 블록)
33	블록 2 (1단계 인덱스 블록)
65	블록 3 (1단계 인덱스 블록)
97	블록 4 (1단계 인덱스 블록)
...	...
961	블록 31 (1단계 인덱스 블록)

31개의 블록을 블록인덱싱 테이블에 담았다

2단계 인덱스 블록은 1단계 인덱스 블록을 구분하는 "경계선 역할"을 함
➡ 예를 들어, eid=50을 찾는다면 eid=33부터 eid=65 사이에 있으므로, 블록 2로 이동하면 됨!
➡ 블록 2에는 33~64까지 eid가 인덱싱 되어있음

1레코드는 = 128byte, 4레코드 = 512byte
1블록 = 512byte까지 저장가능

즉, 인덱싱안한 1000개의 레코드를 찾기위해선
디스크내의 250블록을 무작위 찾아야했다.

그러나 eid와 pointer 속성만 존재하는(16byte)하게하 바이트수를 줄인
1단계로 인덱싱을 하고 나서는
디스크 수내의 블록이 31개만 필요하게 됐고

그 블록들을 블록 인덱싱 테이블에 다시 2단계로 인덱싱하여
31개의 블록들을 1개의 블록에 담았다

이제 블록 인덱싱 테이블(2단계 인덱싱)에서 eid=50을 찾을때
50이 속한 블록 을찾고
그 블록내의 eid들 속에서만 eid를 찾아 포인터로 실제 테이블에 eid로 접근하면되니 훨씬 빠르게 찾을 수 있다.

✅ 멀티 레벨 인덱싱을 적용하면 탐색 시 최악의 경우에도 3번의 블록 접근만 하면 됨!
➡ (1) 2단계 인덱스 블록 → (2) 1단계 인덱스 블록 → (3) 데이터 블록

🚀 탐색 속도가 대폭 향상됨!

B-tree 방식으로 구조 형성

🔹 1️⃣ 인덱스 증가 → 레벨 증가 → 트리 구조 형성
데이터베이스의 데이터가 많아질수록 인덱스도 커지고, 블록 수도 증가합니다.
즉, 1단계 인덱스로 모든 데이터를 관리하기 어려워지고, 상위 인덱스(2단계 인덱스)가 필요하게 됩니다.

✅ 이렇게 인덱스가 여러 단계로 늘어나면서 자연스럽게 "트리(Tree) 구조"가 형성됩니다.
✅ 즉, Multi-Level Indexing이 발전하여 자동으로 "트리 계층 구조"를 가지게 됨.

🔹 2️⃣ B-Tree 자료구조의 등장: 인덱스를 자동으로 최적화
문제:

인덱스가 여러 레벨로 증가하면 인덱스 관리가 어려워짐
각 인덱스를 균형 있게 유지해야 탐색 속도가 최적화됨
데이터를 추가하거나 삭제할 때 균형이 무너질 위험이 있음

해결:
➡ 이 문제를 해결하기 위해 등장한 것이 바로 B-Tree!
➡ B-Tree는 인덱스 노드가 자동으로 정렬되고, 균형을 유지하여 탐색이 일정한 속도로 유지되도록 관리

데이터베이스는 B-tree계열의 B+tree를 사용

B-Tree는 삽입/삭제 시 데이터가 내부 노드 & 리프 노드에 분산 저장되므로, 리프 노드 간 정렬이 깨짐!
B+ Tree는 내부 노드에는 탐색 키만 저장하고, 모든 데이터를 리프 노드에 저장!
즉, 데이터는 각 리프노드에 정렬된 상태로 저장되고 모든 리프노드는 정렬된 상태를 유지함
리프 노드를 Linked List로 연결하면 순서가 항상 보장됨!

B+ Tree의 주요 특징

내부 노드(Internal Node)에는 데이터가 없고, 탐색을 위한 키 값만 저장
모든 데이터는 리프 노드(Leaf Node)에만 저장
리프 노드끼리 Linked List로 연결되어 있어, 순차 검색(Sequential Search)이 빠름
삽입, 삭제 시 자동으로 균형(Balanced)이 유지됨
트리의 높이가 낮아져 탐색 성능이 향상됨 (O(log n))

B+ Tree 예제

        [30, 50]  <-- (내부 노드: 탐색용 인덱스)
       /    |    \
[10, 20] → [30, 40] → [50, 60, 70]  <-- (리프 노드: 실제 데이터 저장, Linked List 연결)

내부 노드 [30, 50] → 탐색을 위한 인덱스 역할 (데이터 저장 X)
리프 노드 [10, 20] → [30, 40] → [50, 60, 70]
→ 모든 데이터는 리프 노드에 저장
→ 리프 노드는 Linked List로 연결됨 (범위 검색 최적화!)

Linked List 연결이 중요한 이유 (범위 검색 최적화)

✅ 트리 탐색만으로는 하나의 특정 값(eid=50)을 찾는 것은 빠름
✅ 하지만 범위 검색(Range Query)에서는 트리 탐색만으로는 비효율적임
✅ Linked List로 연결하면 범위 검색이 훨씬 빠름!

📌 예제: eid=30 이상 모든 데이터를 검색하는 경우

트리 탐색을 통해 eid=30이 있는 리프 노드에 도착

이후, Linked List를 따라가면서 eid=40, 50, 60, 70...을 순차적으로 탐색
➡ 이 과정에서 트리를 다시 탐색하지 않아도 됨!

✅ 트리 탐색만 사용하면?

eid=30을 찾은 후, 다음 값을 찾을 때 다시 트리를 탐색해야 함

트리를 여러 번 탐색해야 하므로 비효율적!

✅ Linked List가 연결되어 있으면?

한 번 트리에서 시작 지점을 찾으면, 이후에는 Linked List를 따라 순차 검색 가능!

범위 검색 속도가 대폭 향상됨! 🚀

Psj

Software Developer