Classification
데이터 분류
load fisheriris
f = figure;figure
새 창을 생성한다
꽃받침 측정값을 포함하는 두 열 사용
gscatter(meas(:,1), meas(:,2), species,'rgb','osd');
xlabel('Sepal length');
ylabel('Sepal width');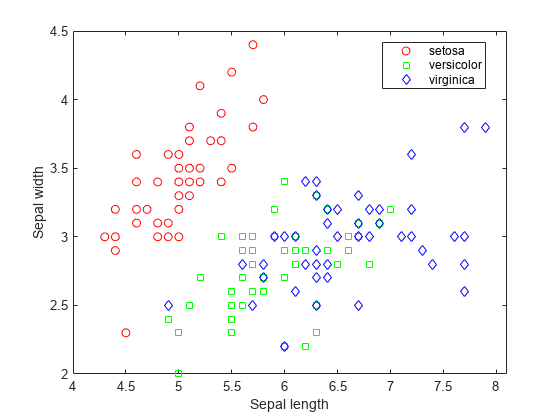
meas(rows, cols)
행렬 meas는 150개의 서로 다른 꽃에 대한 꽃 측정치(꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비)를 포함한다.
species
150*1의 행렬
gscatter(x, y, group, color, osd)
그룹(species)별 산점도 플롯으로 각 그룹에 대해 마커 색(rgb), 기호(osd)를 지정한다.
판별분석
측정값을 기반으로 하여 어떤 값을 판별해야 한다고 할 때, 각 집단에서 추출된 표본들의 측정값을 이용하여 이 표본들이 어느 모집단에서 추출된 것인지를 결정해주는 분석법을 말한다.
LDA(선형판별분석)
지도 학습에서 classification(분류)과 dimensional(차원 축소)를 동시에 사용하는 알고리즘으로 데이터를 하나의 선으로 투영시킨다. LDA는 같은 class들의 데이터는 분산이 최소화되고 다른 class간에는 분산이 최대화 되도록 해서 clss가 잘 구분되도록 데이터들을 투영한다.
lda = fitcdiscr(meas(:,1:2),species);
ldaClass = resubPredict(lda);fitcdiscr(Table, ResponseVarName)
Table에 포함된 입력 변수(속성)와 ResponseVarName에 포함된 출력(응답 or 레이블)을 기반으로 적합 판별 분석 모델을 반환합니다.
resubPredict
훈련된 회귀 모델을 사용하여 훈련 데이터에 대한 출력(응답 or 레이블) 예측
ldaResubErr = resubLoss(lda)resubLoss
훈련 데이터 세트에 대한 오분류 오차를 계산
figure
ldaResubCM = confusionchart(species,ldaClass);confusionchart(i, j)
훈련 데이터 셋에 대한 혼동 행렬을 계산합니다. 일반적으로, 혼동행렬에서 i는 알려진 클래스 레이블이고 j는 에측된 클래스 레이블입니다. 대각선 요소는 올바르게 분류된 관측값을 나타냅니다.
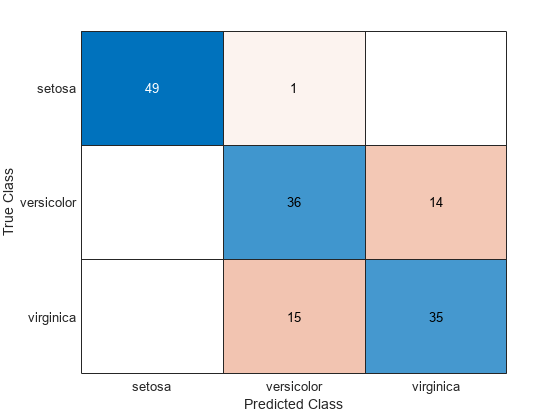
150개의 훈련 측정값의 20%인 30개 관측값이 선형 판별분석 함수에 의해 오분류되었습니다.
오분류된 점을 x로 그려 표시
figure(f)
bad = ~strcmp(ldaClass,species);strcmp
문자열 비교 함수, 둘이 동일하며 1을 반환하고 동일하지 않으면 0을 반환한다.
hold on;
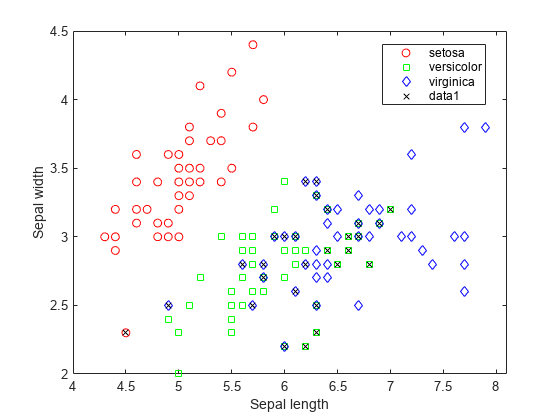
plot(meas(bad,1), meas(bad,2), 'kx');
hold off; %그려진 bad에 기존 플롯 추가hold
-
on
좌표축에 플롯이 새로 추가될 때 기존 플롯이 삭제되지 않도록 현재 좌표축의 플롯을 유지합니다. -
off
유지 상태를 꺼짐으로 설정하여, 좌표축에 플롯이 새로 추가될 경우 기존 플롯을 지우고 모든 axes 속성을 재설정하도록 합니다.
plot(x,y,LineSpec)
x값에 대한 y 데이터의 2차원 선 플롯을 생성하는데, 지정된 선 스타일을 사용하여 플롯을 만듭니다
[x,y] = meshgrid(4:.1:8,2:.1:4.5);
x = x(:);
y = y(:);meshgrid(x, y)
시작할 수, 증가할 수, 마지막 수의 행렬을 포함한 x값과 y값으로 구성된 그리드 생성
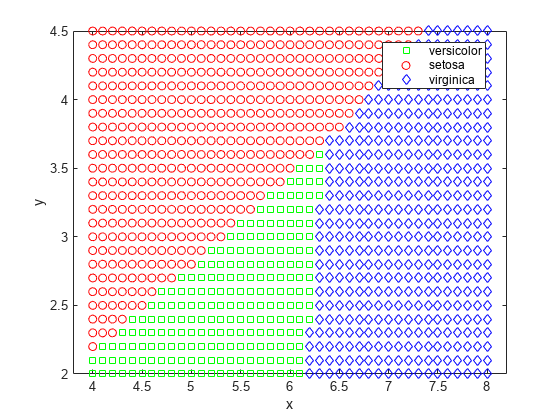
j = classify([x y],meas(:,1:2),species);
gscatter(x,y,j,'grb','sod')classify(sample, training, group)
sample에 있는 데이터의 각 행을 training에 있는 데이터가 속한 그룹 중 하나로 분류합니다. 이 함수는 sample의 각 행에 할당된 그룹을 포함하는 클래스를 반환합니다.
QDA(2차판별분석)
지도 학습에서 사용하는 비선형 분류 방식
교차 검증을 수행하여 검정 오차를 추정
Test error(검정 오차)
train data로 구한 모델에 test data를 적용했을 때의 추정값과 실제값의 차이의 MSE
교차 검증
데이터를 훈련용과 검증용으로 교차 선택하여 여러 모델을 학습하고 성능을 평가하는 방법
rng(0, 'twister');
cp = cvpartition(species,'KFold',10)predict(detector, I)
테스트 이미지 I에 대해 추론하는 동안 변칙 탐지기가 예측한 비정규화된 변칙 점수를 계산한다. 이 함수를 사용하여 추론 중에 검출기의 출력 레이어에서 예측값을 가져옵니다.
나이브 베이즈
조건부 확률을 비교하여 더 높은 확률값의 클래스를 선택하는 분류기로, 적은 수의 데이터로도 훈련이 가능한 장점이 있다.
가우스 분포를 사용하여 각 클래스에 포함된 각각의 변수를 모델링한다.
nbGau = fitcnb(meas(:,1:2), species);fitcnb(X, Y, DistributionName, value, kernel, value)
다중 클래스 나이브 베이즈 모델 학습 함수
오분류 오차와 교차 검증 오차 계산
nbGauResubErr = resubLoss(nbGau)
nbGauCV = crossval(nbGau, 'CVPartition', cp);
nbGauCVErr = kfoldLoss(nbGauCV)영역 시각화
labels = predict(nbGau, [x,y]);
gscatter(x, y, labels, 'grb', 'sod')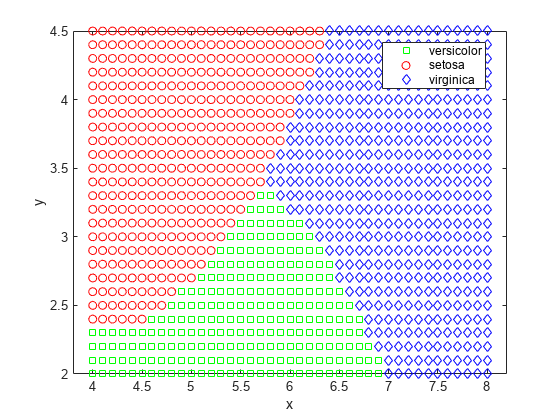
밀도 추정
관측된 데이터(측정값)로부터 변수(예측값)가 가질 수 있는 모든 값의 확률(밀도)을 추정하여 변수의 특성을 파악하는 방법이다.
-
Parametric(모수 추정법)
관측된 데이터를 바탕으로 관심 대상인 확률 변수가 특정 분포를 따른다는 가정 하에 확률 밀도를 추정하는 방법이다. -
Non-parametric(비모수 추정법)
특정 분포를 가정하지 않기 때문에 모수를 구하지 않고도 확률 밀도를 추정할 수 잇는 방법이다.
KDE(커널 밀도 추정)
비모수 추정법 중 하나로, 커널 함수와 데이터를 바탕으로 연속성 있는 확률 밀도 함수를 추정하는 방법이다.
nbKD = fitcnb(meas(:,1:2), species, 'DistributionNames','kernel', 'Kernel','box');
nbKDResubErr = resubLoss(nbKD)오분류 오차와 교차 검증 오차 계산
nbKDResubErr = resubLoss(nbKD)
nbKDCV = crossval(nbKD, 'CVPartition',cp);
nbKDCVErr = kfoldLoss(nbKDCV)영역 시각화
labels = predict(nbKD, [x y]);
gscatter(x,y,labels,'rgb','osd')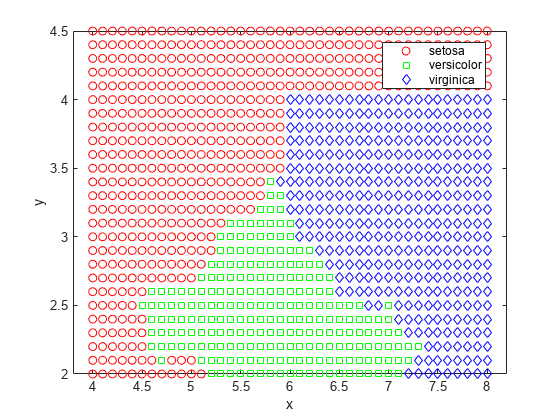
결정 트리
t = fitctree(meas(:,1:2), species,'PredictorNames',{'SL' 'SW' });fitctree(x, y, PredictorNames, value)
결정 트리를 생성한다.
[grpname,node] = predict(t,[x y]);
gscatter(x,y,grpname,'grb','sod')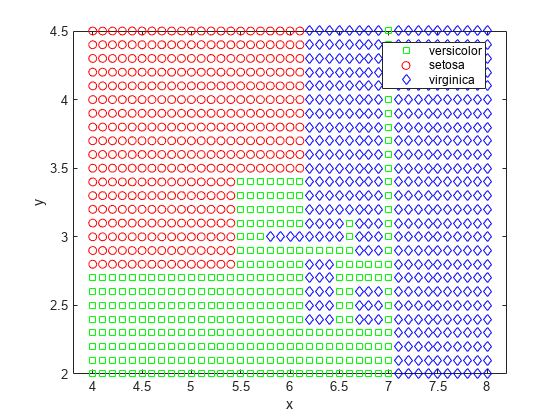
결정 트리를 시각화하는 또 다른 방법으로 결정 규칙과 클래스 할당을 보여주는 도식을 그린다.
view(t,'Mode','graph');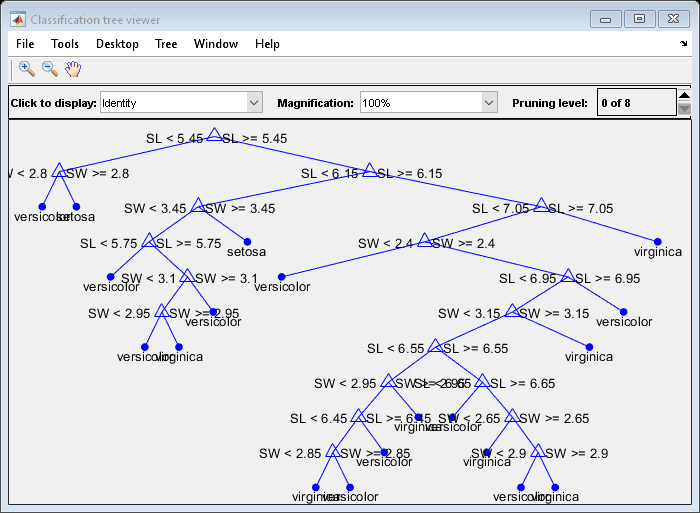
트리 가지치기
생성된 트리가 훈련 세트에 과적합되어 예측 성능이 저하될 가능성이 높기 때문에 가지치기를 사용한다.
resubcost = resubLoss(t, 'Subtrees', 'all');
[cost, secost, ntermnodes, bestlevel] = cvloss(t, 'Subtrees', 'all');[E, SE, Nleaf, BestLevel] = cvloss(tree, Name, Value)
cvloss는 가장 최적의 트리 가지치기 level을 반환한다. 원래 트리의 오분류 오차를 계산하고 하나 이상의 Name, Value 쌍 인수로 지정된 하위 트리에 대한 교차 검증을 계산합니다.
plot(ntermnodes,cost,'b-', ntermnodes,resubcost,'r--')
figure(gcf);
xlabel('Number of terminal nodes');
ylabel('Cost (misclassification error)')
legend('Cross-validation','Resubstitution')