백준 14501 퇴사

박철현·2024년 4월 21일

백준

Java

목록 보기

7/13

백준 - 퇴사

풀이1 - 빽트래킹

아이디어

퇴사일 까지도 1일 걸리는 상담은 할 수 있음
시작일 부터 기준이 되는 날에서 상담을 하거나 하지 않거나의 총 두가지 경우의 수가 생김
위 아이디어를 트리구조로 나타내면 아래와 같음
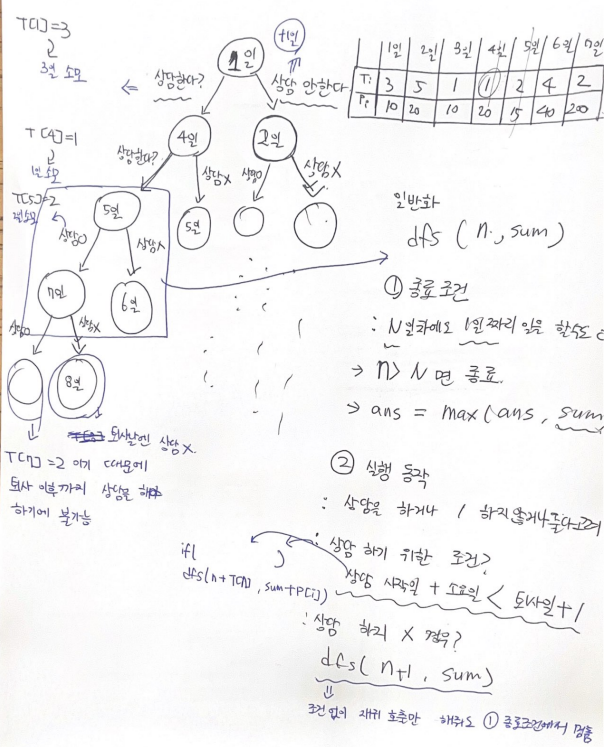
- 기준일 기준 상담 진행 또는 진행x 선택
- 모든 경우의 수 확인

코드

import java.io.*;
import java.util.*;

public class Main {
    static int answer = 0;
    static int[] dayArr;
    static int[] payArr;
    static int N;
    public static void main(String[] args) throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        dayArr = new int[N + 1];
        payArr = new int[N + 1];
        // 1. 상담 일자별 소요일수, pay 초기화
        for(int i = 1; i <= N; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            dayArr[i] = Integer.parseInt(st.nextToken());
            payArr[i] = Integer.parseInt(st.nextToken());
        }
        // 2. dfs 탐색 시작
        dfs(1, 0); 
        // 3. 정답 출력
        System.out.println(answer);
    }
    
    public static void dfs(int day, int sum) {
        // 1. 종료 조건
        if(day >= N + 1) { // 퇴사 다음날 이상 초과할 경우
            answer = Math.max(answer, sum);
            return;
        }
        // 2. 반복 수행 -> N일차때 1일 걸리는 상담 하면 N+1일이 기준이 되니깐
        if(day + dayArr[day] <= N + 1) {
            // 상담 진행
            dfs(day + dayArr[day], sum + payArr[day]);
        }
        // 상담 진행x
        dfs(day + 1, sum);
    }
        
}

비고

시간 복잡도 : O(2^15)
- 15 이하라고 나와있음, 각 일마다 상담o or 하지x
- 보통 이진트리 형태면 50까지 풀 수 있음
- 2^15 => 2^10 2^5 => 10^3 32 => 대략 320,000로 연산 가능
빽트래킹 : 현재 상태에서 더 이상 진행할 수 없는 경우 이전 상태로 돌아가 다른 경로를 시도하는 방식
- 적용점 : 사전에 상담이 불가능하면 상담하는 경우의 수 포함하지 않음

풀이2 - DP

아이디어

만일 2^100 처럼 50가지 이상이 넘는다면? 빽트래킹으로 불가능
완료나 특정 경우엔 역방향이 풀이가 간편해지는 경우가 있는데 이 경우가 그럼
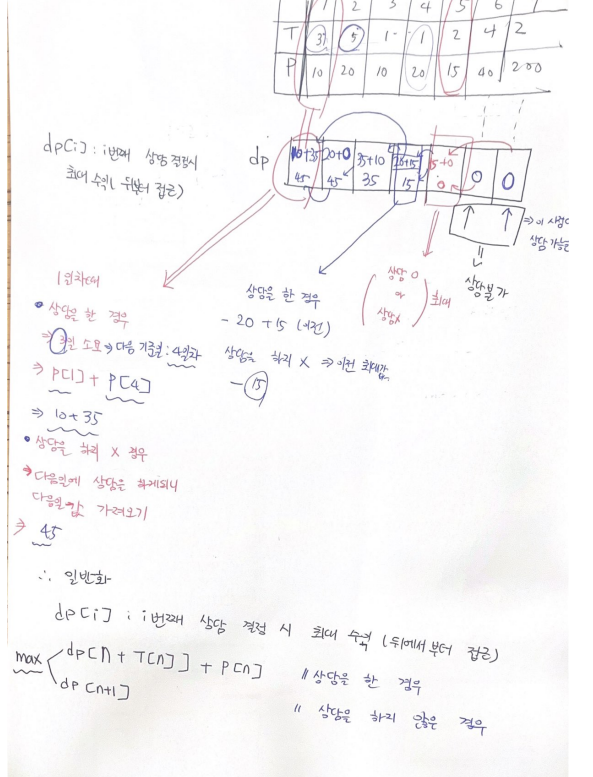
dp[i] : i번째 일자에서 상담 결정 시 최대 수익(뒤에서 부터 접근)
- 7일차, 6일차 : 상담 잡기가 불가능 => 최대 0의 수익
- 5일차 : 상담 2일 걸리니 잡기가 가능
  - 상담을 잡는 경우 : 5일차 수익 + 2일 뒤 상딤 = 6일차에서 상담 결정 시 최대 수익
    - 5일차 수익 : 15 + 7일차 최대 수익 0 = 15
  - 상담을 잡지 않는 경우 : 5일차에 안잡으면 6일차 수익과 같아짐
    - 5일차 수익 = 6일차 최대 수익 => 0
- 4일차 : 상담 1일 걸리니 잡기 가능
  - 상담을 잡는 경우 : 4일차 상담으로 인한 수익 + 5일차 최대 수익
    - 20 + 15 = 35
  - 상담을 잡지 않는 경우 : 다음날 최대 수익과 같음 => 5일차
    - 15
- 3일차 : 상담 1일 걸리니 상담 잡기 가능
  - 상담을 잡는 경우 : 3일차 상담으로 인한 수익 + 4일차 최대 수익
    - 35 + 10 = 45
  - 상담을 잡지 않는 경우 : 4일차 최대 수익과 같음
    - 35
- 일반화
  - dp[i] = Max(dp[n + T[n]] + p[n], dp[n+1])
  - 상담을 하거나 하지 않거나 중 최대 수익

코드

import java.io.*;
import java.util.*;

public class Main {
    static int[] dayArr;
    static int[] payArr;
    static int N;
    public static void main(String[] args) throws Exception{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        int[] D = new int[N + 2];
        dayArr = new int[N + 1];
        payArr = new int[N + 1];
        // 1. 상담 일자별 소요일수, pay 초기화
        for(int i = 1; i <= N; i++) {
            StringTokenizer st = new StringTokenizer(br.readLine());
            dayArr[i] = Integer.parseInt(st.nextToken());
            payArr[i] = Integer.parseInt(st.nextToken());
        }
        // 2. dp배열 생성 : i번째 일자에 최대 수익
        for(int i = N; i > 0; i--) {
            // 퇴사일 이후에 끝나는 상담이라면, 상담을 못하니깐 최대 수익은 상담을 하지 않는 것
            // 예시로 퇴사 바로 전날인 7일차 떄 1일 걸리는 작업까지는 가능
            // 7일차 때 1일차 작업 -> 7 + 1 = 8(N + 1)
            // N + 1을 초과한다면 상담은 불가능 하니 이전 상담 최대 수익으로 갱신
            if(i + dayArr[i] > N + 1) {
                D[i] = D[i+1];
            }
            // 여기서 이제 상담을 안하는 것과, 상담을 하는 것 중 최대값을 선정
            else {
                D[i] = Math.max(D[i + 1], D[i + dayArr[i]] + payArr[i]);
            }
        }
        // 3. 정답 출력
        System.out.println(D[1]);
    }   
}