백준 13398 연속합 2

백준 - 연속합

아이디어

• a + b = c (c가 만일 최대값)
  • b + a = c (덧셈 교환법칙 성립)
  • 왼쪽부터 DP하여 구한 최대값 == 오른쪽부터 DP하여 구한 최대값
• 최대값
  • 요소 하나도 제거 하지 않은 경우 : 왼쪽 dp == 오른쪽 dp
  • 요소 하나 제거(제거한 index : idx)
    - idx 기준 왼쪽에 최대값
    - idx 기준 오른쪽에 최대값
    - idx 양 옆에 더한 값이 최대값
    
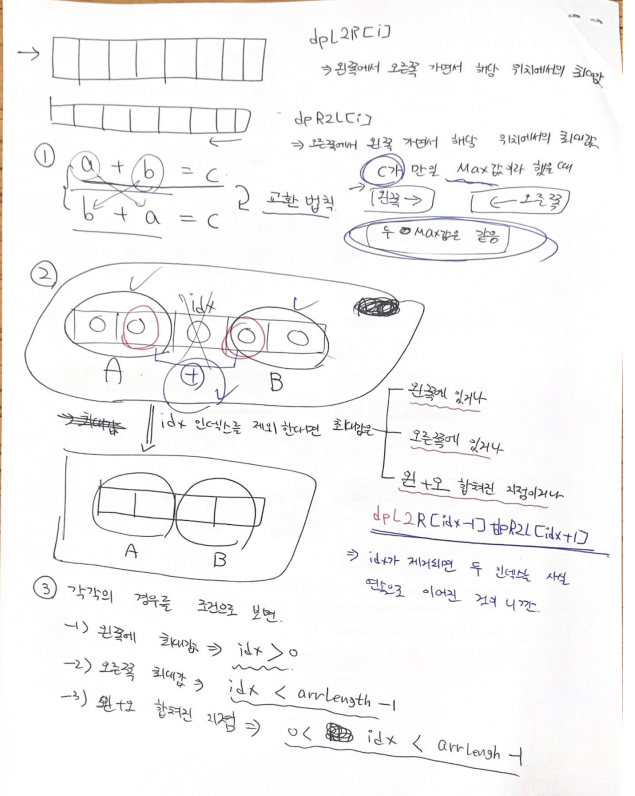
• dpL2R[i] : 왼쪽부터 수열 이동하면서 최대 합 저장
• dpR2L[i] : 오른쪽부터 수열 이동하면서 최대 합 저장

코드

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int N = Integer.parseInt(br.readLine());
        int[] arr = new int[N];
        StringTokenizer st = new StringTokenizer(br.readLine());
        // 1. 데이터 초기화
        for(int i = 0; i < N; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }
        // 2. dp 수행
        int[] dpL2R = new int[N];
        dpL2R[0] = arr[0];
        int[] dpR2L = new int[N];
        dpR2L[N-1] = arr[N-1];
        int max = arr[0]; 
        
        // 2-1. 왼쪽 dp 완성
        for(int i = 1; i < dpL2R.length; i++) {
            dpL2R[i] = Math.max(dpL2R[i - 1] + arr[i], arr[i]);
            max = Math.max(max, dpL2R[i]); // 일단 아무것도 안뺏을 때 최대값(안뺄수도 있으니)
        }
        
        // 2-2. 오른쪽 dp 완성
        for(int i = N - 2; i >=0; i--) {
            dpR2L[i] = Math.max(dpR2L[i + 1] + arr[i], arr[i]);
        }
        
        // 3. 인덱스 하나씩 빼면서 최대값 찾기
        for(int idx = 0; idx < N; idx++) {
            // 왼쪽에 최대값이 있는지 확인
            if(idx > 0) {
                max = Math.max(max, dpL2R[idx - 1]);
            }
            // 오른쪽에 최대값이 있는지 확인
            if(idx < N-1) {
                max = Math.max(max, dpR2L[idx + 1]);
            }
            // idx전, 후 합해야 하는지 확인
            if(idx > 0 && idx < N - 1) {
                max = Math.max(max, dpL2R[idx - 1] + dpR2L[idx + 1]);
            }
        }
        
        // 4. 최대값 출력
        System.out.println(max);
    }
}

비고

• 시간 복잡도 : O(n)
  • dpL2R (n) + dpR2L (n) + idx 하나씩 빼기 => O(3n)
• 어렵구만..

출처

• BOJ 13398번 연속합 2 - O(N) 풀이