⚒ 자료구조 스터디 ⚒
📂BFS
✅BFS란
- Breadth First Search의 약자이며, 너비 우선 탐색이라고 불린다.
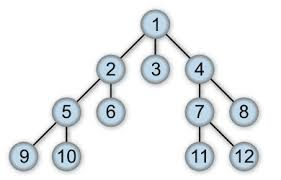
- 루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법
❓어디서 쓰나요❓
- 미로 찾기 등 최단 거리 구하기
- 네트워크 탐색
📂BFS
✅구현
- Queue 자료구조를 이용한다.
🔎 장점
1. 출발노드에서 목표노드까지의 최단 길이 경로를 보장한다.
🔎 단점
1. 경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 기억 공간을 필요로 하게 된다.
2. 해가 존재하지 않는다면 유한 그래프(finite graph)의 경우에는 모든 그래프를 탐색한 후에 실패로 끝난다.
3. 무한 그래프(infinite graph)의 경우에는 결코 해를 찾지도 못하고, 끝내지도 못한다.
📐문제풀이
🚩백준: 실버2 - Q24446 너비 우선 탐색 3
문제
입력
첫째 줄에 정점의 수 N (5 ≤ N ≤ 100,000), 간선의 수 M (1 ≤ M ≤ 200,000), 시작 정점 R (1 ≤ R ≤ N)이 주어진다.
다음 M개 줄에 간선 정보 u v가 주어지며 정점 u와 정점 v의 가중치 1인 양방향 간선을 나타낸다. (1 ≤ u < v ≤ N, u ≠ v) 모든 간선의 (u, v) 쌍의 값은 서로 다르다.
출력
첫째 줄부터 N개의 줄에 정수를 한 개씩 출력한다. i번째 줄에는 정점 i의 깊이를 출력한다.
시작 정점 R의 깊이는 0이고 방문 되지 않는 노드의 깊이는 -1로 출력하자.
예시
🔻 입력값 🔻
5 5 1
1 4
1 2
2 3
2 4
3 4
🔻 출력값 🔻
0
1
2
1
-1
✅백준 - Q24446 문제풀이
🎯 처음 구상도
1. 인접리스트를 사용한다.
2. 깊이 관련 배열 하나를 생성하고 -1로 초기화한다.
3. BFS를 Queue를 통해 구현하고 Node끼리의 관계를 이용해 첫번째 노드부터 깊이를 매긴다.
❓원래 순서 출력하는 값을 가져와서 배열 추가만 했다.
💻결과 코드
public class Silver2_Q24446 {
static ArrayList<Integer>[] Node;
static int[] visited;
static int visitNode = 1;
static int[] arr;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
int R = Integer.parseInt(st.nextToken());
Node = new ArrayList[N+1];
for (int i=0; i<N+1; i++){
Node[i] = new ArrayList<>();
}
visited = new int[N+1];
for (int i=0; i<M; i++){
st = new StringTokenizer(br.readLine(), " ");
int A = Integer.parseInt(st.nextToken());
int B = Integer.parseInt(st.nextToken());
Node[A].add(B);
Node[B].add(A);
}
for (int i =0; i < N+1; i++){
Collections.sort(Node[i]);
}
arr = new int[N];
Arrays.fill(arr, 0);
BFS(R);
for (int i = 0; i < arr.length;i++){
if ( i != R-1 && arr[i] == 0){
arr[i] = -1;
}
System.out.println(arr[i]);
}
// for (int i = 1; i <= N; i++){
// System.out.println(visited[i]);
// }
}
static void BFS(int start){
Queue<Integer> que = new LinkedList<>();
que.offer(start);
visited[start] = visitNode++;
while (!que.isEmpty()){
int curNode = que.poll();
for (int i=0; i<Node[curNode].size(); i++){
int next = Node[curNode].get(i);
if (visited[next] == 0){
que.offer(next);
visited[next]=visitNode++;
arr[next-1] = arr[curNode-1] +1;
}
}
}
}
}
🚩백준: 실버1 - Q7562 나이트의 이동
문제
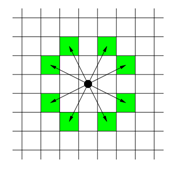
체스판 위에 한 나이트가 놓여져 있다. 나이트가 한 번에 이동할 수 있는 칸은 아래 그림에 나와있다.
나이트가 이동하려고 하는 칸이 주어진다. 나이트는 몇 번 움직이면 이 칸으로 이동할 수 있을까?
입력
입력의 첫째 줄에는 테스트 케이스의 개수가 주어진다.
각 테스트 케이스는 세 줄로 이루어져 있다.
첫째 줄에는 체스판의 한 변의 길이 l(4 ≤ l ≤ 300)이 주어진다.
체스판의 크기는 l × l이다.체스판의 각 칸은 두 수의 쌍 {0, ..., l-1} × {0, ..., l-1}로 나타낼 수 있다.
둘째 줄과 셋째 줄에는 나이트가 현재 있는 칸, 나이트가 이동하려고 하는 칸이 주어진다.
출력
각 테스트 케이스마다 나이트가 최소 몇 번만에 이동할 수 있는지 출력한다.
🔻입력 예시🔻
3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1
🔻출력 예시🔻
5
28
0
🔻입력 예시2🔻
2
✅백준 - Q24479 문제풀이
🎯 처음 구상도
1. 이동하는 값들을 담아놓기 dX, dY
2. 보드판과 방문 표시할 배열 생성
3. 모든 보드판을 돌아다니는 BFS를 생성 후 원하는 위치의 count만 출력
❓ 점화식을 복잡하게 생각하지 않아도 된다.
❌ 실패 이유 분석
이동의 변수가 너무 많다고 생각하고, 이동경로에 대해 너무 깊이 생각했다.
⭕ 해결
해당 위치에 도착한 결과값만 출력하면 OK.
💻결과 코드
// 나이트의 이동
public class Silver1_Q7562 {
static int size;
// 체스판
static int[][] board;
// 나이트의 이동 범위
static int[] dx = {-1, -2, -2, -1, 1, 2, 2, 1};
static int[] dy = {-2, -1, 1, 2, 2, 1, -1, -2};
// 방문 여부
static boolean[][] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
int N = Integer.parseInt(br.readLine());
while (N > 0){
size = Integer.parseInt(br.readLine());
// st = new StringTokenizer(br.readLine(), " ");
String nowLine = br.readLine();
String[] now = nowLine.split(" ");
int nowX = Integer.parseInt(now[0]);
int nowY = Integer.parseInt(now[1]);
String nextLine = br.readLine();
String[] next = nextLine.split(" ");
int nextX = Integer.parseInt(next[0]);
int nextY = Integer.parseInt(next[1]);
// int[] nowP = {Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())};
// int[] nextP = {Integer.parseInt(st.nextToken()), Integer.parseInt(st.nextToken())};
board = new int[size][size];
visited = new boolean[size][size];
if (nowX == nextX && nowY == nextY){
System.out.println(0);
} else {
bfs(nowX, nowY);
System.out.println(board[nextX][nextY]);
}
N--;
}
}
static void bfs(int x, int y){
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{x, y});
visited[x][y] = true;
while (!queue.isEmpty()){
int[] start = queue.poll();
int nowX = start[0];
int nowY = start[1];
for (int i =0; i < 8; i++){
int newX = nowX + dx[i];
int newY = nowY + dy[i];
if (newX >= 0 && newX < size){
if (newY >= 0 && newY < size){
if (!visited[newX][newY]){
queue.add(new int[]{newX, newY});
board[newX][newY] = board[nowX][nowY] + 1;
visited[newX][newY] = true;
}
}
}
}
}
}
}
🚩백준: 골드3 - Q2206 벽 부수고 이동하기
문제
Q. N×M의 행렬로 표현되는 맵이 있다.
맵에서 0은 이동할 수 있는 곳을 나타내고, 1은 이동할 수 없는 벽이 있는 곳을 나타낸다.
당신은 (1, 1)에서 (N, M)의 위치까지 이동하려 하는데, 이때 최단 경로로 이동하려 한다.
최단경로는 맵에서 가장 적은 개수의 칸을 지나는 경로를 말하는데, 이때 시작하는 칸과 끝나는 칸도 포함해서 센다.
만약에 이동하는 도중에 한 개의 벽을 부수고 이동하는 것이 좀 더 경로가 짧아진다면, 벽을 한 개 까지 부수고 이동하여도 된다.
한 칸에서 이동할 수 있는 칸은 상하좌우로 인접한 칸이다.
맵이 주어졌을 때, 최단 경로를 구해 내는 프로그램을 작성하시오.
입력
첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 1,000)이 주어진다. 다음 N개의 줄에 M개의 숫자로 맵이 주어진다.
(1, 1)과 (N, M)은 항상 0이라고 가정하자.
출력
첫째 줄에 최단 거리를 출력한다. 불가능할 때는 -1을 출력한다.
예시
🔻 입력값 🔻
6 4
0100
1110
1000
0000
0111
0000
🔻 출력값 🔻
15
✅백준 - Q2206 문제풀이
🎯 처음 구상도
1. 이동할 수 있는 경로를 저장
2. 벽을 부쉈는지 여부 저장
3. 방문 여부 저장 (부쉈는지 안부쉈는지도 체킹)
4. 벽 존재 여부에 따라 우르르 바뀜
❓ 벽 부수고 안부수고가 진짜 어려웠다.
❌ 실패 이유 분석
부순 값과 안 부순 값의 차이점을 너무 크게 생각했다.
🔺미해결
블로그를 보면서 아이디어는 얼추 비슷함을 깨달았다.
참고해보면서 풀어볼 예정.
💻결과 코드
public class Gold3_Q2206 {
static int[][] map;
static int[][][] checked;
static boolean[][][] visited;
static int[] dx = {1, -1, 0, 0};
static int[] dy = {0, 0, 1, -1};
static int N, M;
static boolean destroyed;
static int count;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
checked = new int[N][M][2];
destroyed = false;
map = new int[N][M];
visited = new boolean[N][M][2];
for (int i =0; i < N; i++){
String line = br.readLine();
for (int j = 0; j < M; j++){
map[i][j] = line.charAt(j) - '0';
}
}
count = 1;
bfs(0, 0);
System.out.println(checked[N-1][M-1][0]);
// System.out.println(count);
}
static void bfs(int x, int y){
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{x, y});
while (!queue.isEmpty()){
int[] start = queue.poll();
int nowX = start[0];
int nowY = start[1];
if (!destroyed){
visited[nowX][nowY][0] = true;
} else {
visited[nowX][nowY][1] = true;
}
for (int i =0; i < 4; i++){
int newX = start[0] + dx[i];
int newY = start[1] + dy[i];
if (newX >= 0 && newX < N){
if (newY >= 0 && newY < M){
count++;
// 벽이 아닐때
if (map[newX][newY] == 0){
// 부순 벽이 없을때
if (!destroyed && !visited[newX][newY][0]){
queue.add(new int[]{newX, newY});
checked[newX][newY][0] = checked[nowX][nowY][0] + 1;
visited[newX][newY][0] = true;
}
// 부순 벽이 있을때
else if (destroyed && !visited[newX][newY][1]){
queue.add(new int[]{newX, newY});
checked[newX][newY][1] = checked[nowX][nowY][1] + 1;
visited[newX][newY][1] = true;
}
// 벽일때
} else if (map[newX][newY] == 1){
// 부순 벽이 없을 때 부수기
if (!destroyed){
queue.add(new int[]{newX, newY});
checked[newX][newY][1] = checked[nowX][nowY][0] + 1;
visited[newX][newY][1] = true;
destroyed = true;
}
}
}
}
}
}
}
}
