⚒ 자료구조 스터디 ⚒
📂DP
✅DP
- Dynamic Programing의 약자이며, 동적 계획법이라고 불린다.
- 복잡한 문제를 부분부분 나누어 푸는 기법이다.
- 상향식 접근(Bottom-Top)과 하향식 접근(Top-Down)으로 푸는 방법이 나누어져 있다.
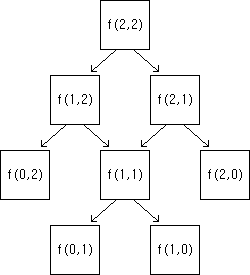
이런식으로 큰 문제들을 나누어 구하여 답을 찾아 나간다.
❓어디서 쓰나요❓
- 검색
- 그래프 탐색
- 정렬
📂상향식 접근(Bottom-Top)
Tabulation
✅구현
- 반복문을 사용한다.
🔎 장점
1. 쉽게 코드의 구조를 이해할 수 있다.
2. 작은 문제들을 확실하게 구해나가서, 최적 부분 구조를 보장한다.
📂하향식 접근(Top-Down)
Memoization
✅구현
- 재귀 함수를 사용한다.
🔎 장점
1. 재귀를 이용하기에 구현이 간단 할 수 있다.
2. 계산 시간이 줄어든다.
📐문제풀이
🚩백준: 실버3 - Q9461 파도반 수열
문제
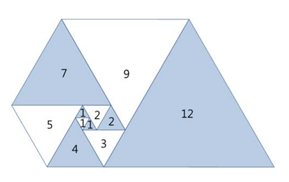
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다.
그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다.
나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다.
P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다.
각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
예시
🔻 입력값 🔻
2
6
12
🔻 출력값 🔻
3
16
✅백준 - Q9461 문제풀이
🎯 처음 구상도
1. DP문제니까 규칙을 먼저 파악했다.
2. N이 4 이상일 때, 규칙 발견 f(n) = f(n-2) + f(n-3)
3. Top-Down 방식으로 풀어보았다.
❓ 세운 점화식이 맞는지를 확인하려고 오래 걸렸다.
💻결과 코드
// 파도반 수열 f(n) = f(n-2) + f(n-3)
public class Silver3_Q9461 {
// 테스트 케이스 갯수
static int T;
// 메인
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
DP = new long[101];
DP[1] = DP[2] = DP[3] = 1;
T = Integer.parseInt(br.readLine());
while (T-- > 0){
int n = Integer.parseInt(br.readLine());
topDown(n);
sb.append(DP[n]).append("\n");
}
System.out.println(sb);
}
/* 탑 다운 방식*/
static long[] DP;
static long topDown(int n){
if (DP[n] == 0) {
DP[n] = topDown(n-2) + topDown(n-3);
}
return DP[n];
}
}
🚩백준: 골드5 - Q2225 합분해
문제
0부터 N까지의 정수 K개를 더해서 그 합이 N이 되는 경우의 수를 구하는 프로그램을 작성하시오.
덧셈의 순서가 바뀐 경우는 다른 경우로 센다(1+2와 2+1은 서로 다른 경우). 또한 한 개의 수를 여러 번 쓸 수도 있다.
입력
첫째 줄에 두 정수 N(1 ≤ N ≤ 200), K(1 ≤ K ≤ 200)가 주어진다.
출력
첫째 줄에 답을 1,000,000,000으로 나눈 나머지를 출력한다.
🔻입력 예시🔻
20 2
🔻출력 예시🔻
21
🔻입력 예시2🔻
6 4
🔻출력 예시🔻
84
✅백준 - Q2225 문제풀이
🎯 처음 구상도
1. 모든 경우의 수를 저장해가며, N까지를 구한다.
2. 각 경우의 수를 담는 이차원 배열을 생성
3. 나눈값들을 저장한다.
4. 이때의 점화식은 DP[N][K] = DP[N-1][K] + DP[N][K-1]
❓ 점화식 너무 어렵다..!
❌ 실패 이유 분석
원래는 나눈 값들을 저장하지 않고, 그 경우의 수 값만 저장해서 마지막 출력할 때 나눠서 결과값을 출력했는데 마지막 부분에서 자꾸 틀렸다.
⭕ 해결
최대값을 입력하니 초과한 수가 나타나서 모든 값들을 나눈 결과값에 저장했다.
💻결과 코드
// 합분해
public class Gold5_Q2225 {
static long[][] DP;
static long sup = 1000000000;
static int N, K;
/* 점화식 -> DP[N][K] = DP[N-1][K] + DP[N][K-1] */
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] line = br.readLine().split(" ");
N = Integer.parseInt(line[0]);
K = Integer.parseInt(line[1]);
DP = new long[N+1][K+1];
for (int i = 0; i <= N; i++){
DP[i][0] = 0;
DP[i][1] = 1;
}
for (int i = 0; i <= K; i++){
DP[1][i] = i;
}
dp();
System.out.println(DP[N][K]);
}
// 출력문에 %를 하면 왜 틀리지.?
static void dp(){
for (int i = 2; i <= N; i++){
for (int j = 2; j <= K; j++){
DP[i][j] = (DP[i-1][j] + DP[i][j-1]) % sup;
}
}
}
}