택배 8980

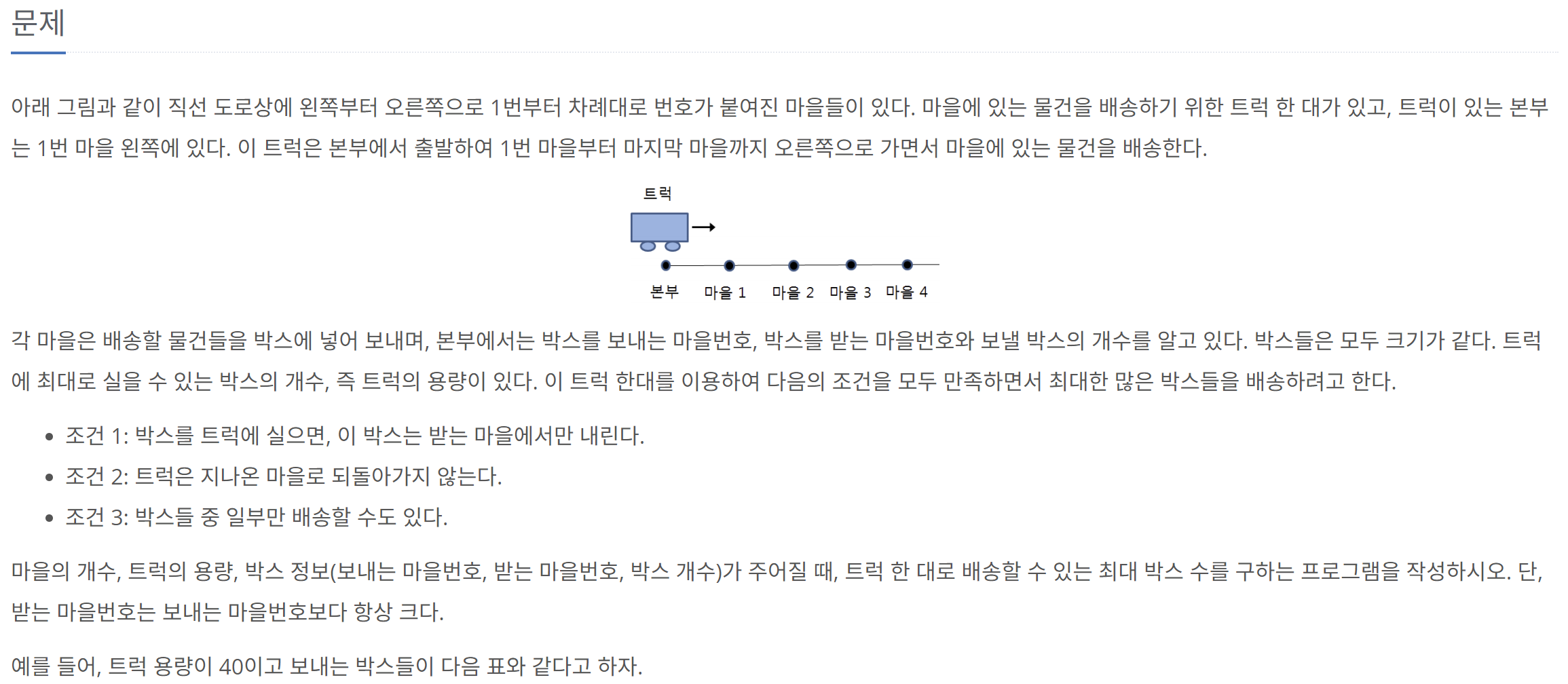
문제

생략

접근 방법

상자를 관리해 주는 방식으로 풀었다.
해당 지점에서 들어갈 수 있는 상자를 다 넣어준다.
이후 도착 마을 번호순으로 정렬한 뒤 C를 넘어가는 값 이후부터는 지워준다. (도착 마을의 번호가 클수록 뒤에 존재하므로 일찍 도착하는 애들만 남는다)
다음 지점에서 도착 마을의 번호가 시작 번호와 같으면 빼주면서 최대 박스 수에 더해준다.

코드

#include <iostream>
#include <vector>
#include <tuple>
#include <queue>
#include <algorithm>
using namespace std;
typedef tuple<int, int, int> tiii;
typedef pair<int, int> pii;
vector<vector<pii>> graph;
vector<pii> boxs;
int N, C, M, startTown, endTown, boxNum, ret;
int main()
{
    ios::sync_with_stdio(0), cin.tie(0);
    cin >> N >> C >> M;
    graph = vector<vector<pii>>(N + 1, vector<pii>());
    while (M--)
    {
        cin >> startTown >> endTown >> boxNum;
        graph[startTown].push_back({endTown, boxNum});
    }
    for (int i = 1; i <= N; ++i)
    {
        sort(boxs.begin(), boxs.end(), greater<pii>());
        while (true)
        {
            if (boxs.empty())
                break;
            if (boxs.back().first <= i)
            {
                ret += boxs.back().second;
                boxs.pop_back();
            }
            else
                break;
        }
        sort(graph[i].begin(), graph[i].end());
        for (pii p : graph[i])
            boxs.push_back(p);
        sort(boxs.begin(), boxs.end());
        int curBox = 0;
        for (int j = 0; j < boxs.size();)
        {
            curBox += boxs[j].second;
            if (curBox > C)
            {
                boxs[j].second = boxs[j].second - (curBox - C);
                boxs.erase(boxs.begin() + j + 1, boxs.end());
                break;
            }
            else
                ++j;
        }
    }
    cout << ret;
    return 0;
}

풀이

비효율적인 코드지만 그래도 풀어서 다행인 것 같다.

최대 택배 개수를 배열로 저장하여서 푸는 방식이 많이 보인다.

M*N의 크기만큼만 확인하면 되기에 시간 효율이 더 높다.