삼각함수
정의: (직각)삼각형의 각도로 양변의 길이를 구하는것
삼각비
- sinθ=빗변높이
- 주기가 2π이며, -1과 1 사이에서 반복
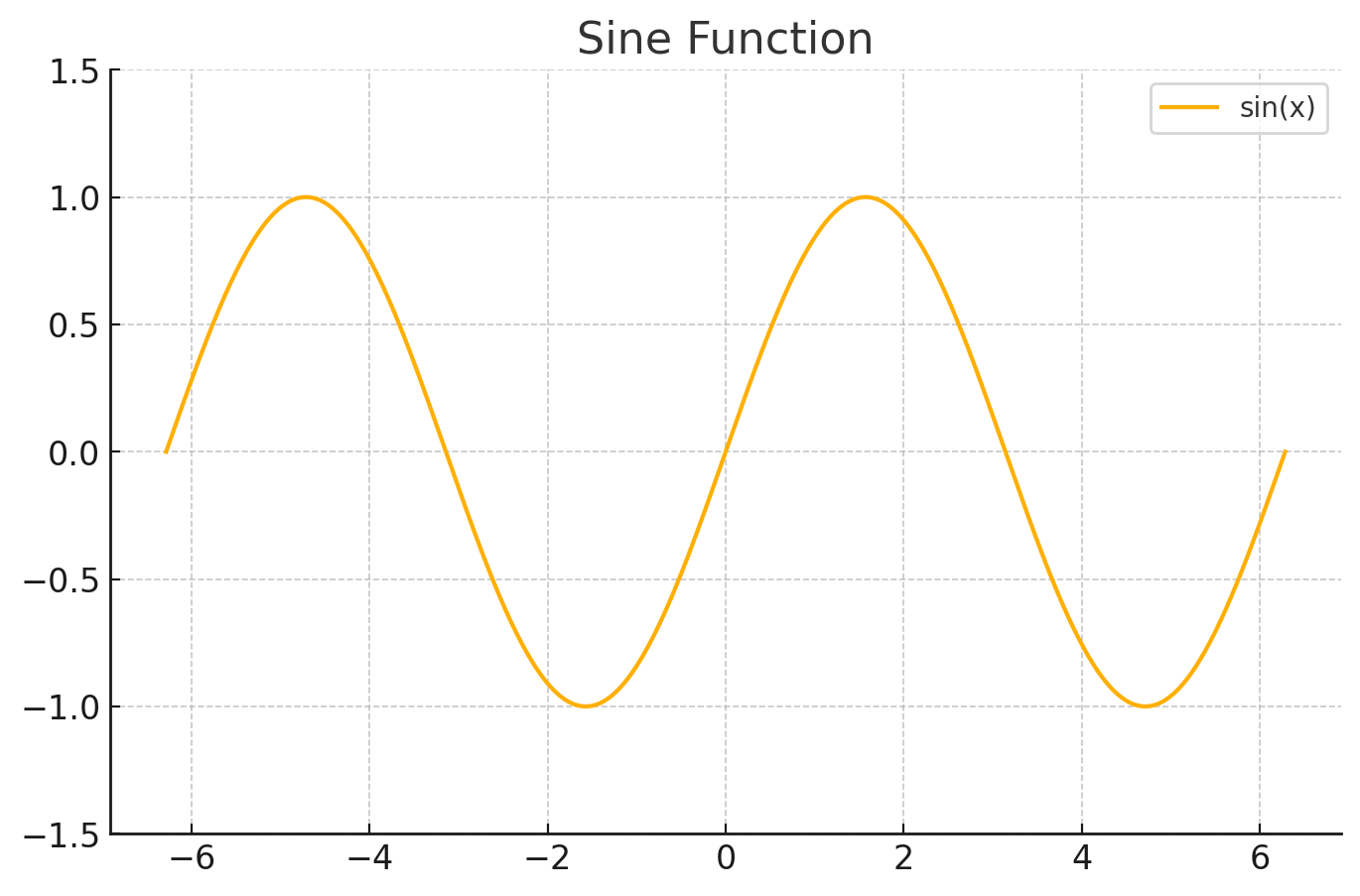
- cosθ=빗변밑변
- 주기가 2π이며, 사인 함수와 비슷하게 -1과 1 사이에서 반복되지만, 위상이 π/2만큼 차이
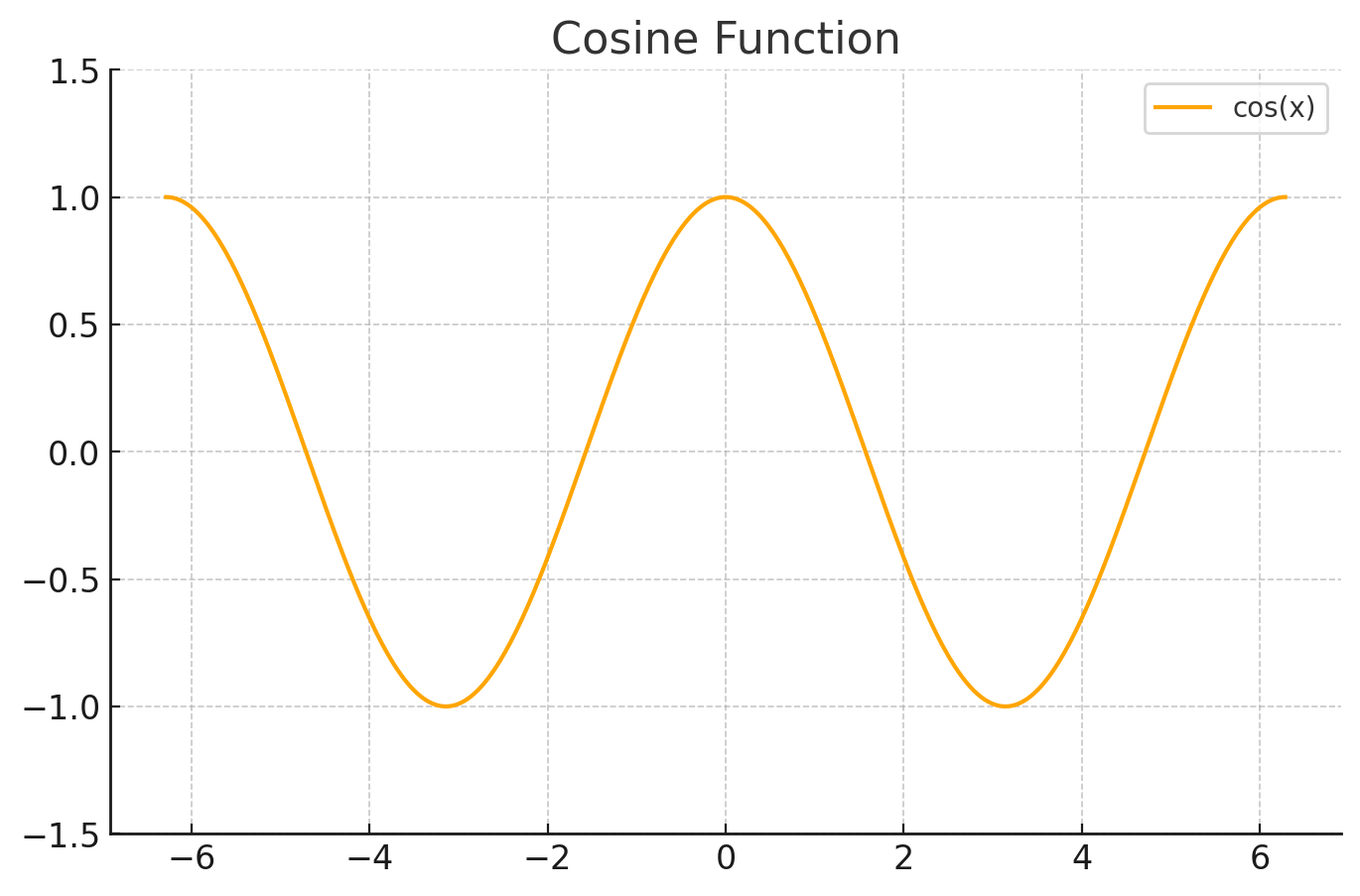
- tanθ=밑변높이
- 주기가 π이며, 특정 각도(예: π/2, 3π/2)에서 비연속적인 극점이 발생
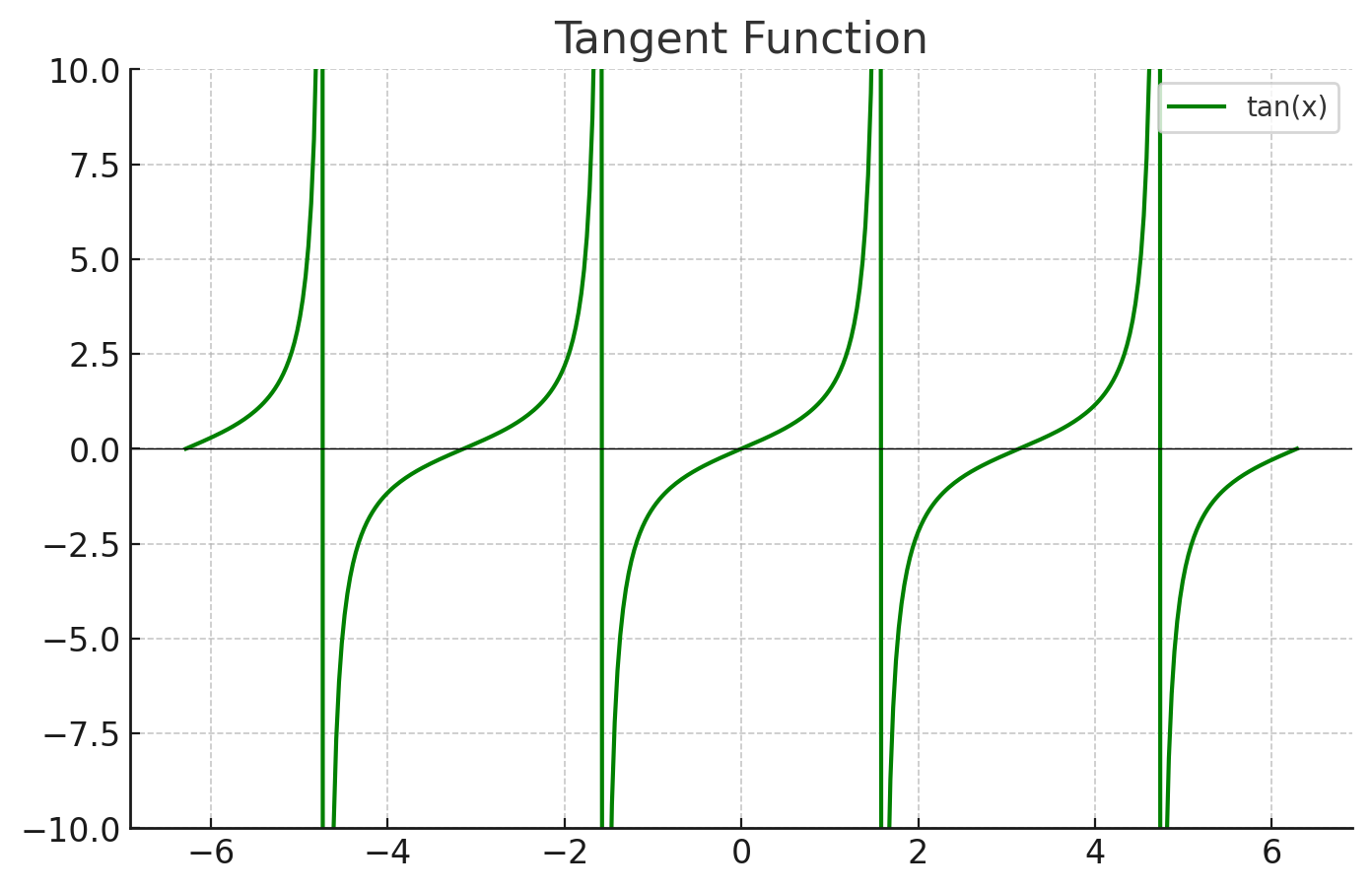
| 각도 | sinθ | cosθ | tanθ |
|---|
| 0° | 0 | 1 | 0 |
| 30° | 21 | 23 | 31 |
| 45° | 22 | 22 | 1 |
| 60° | 23 | 21 | 3 |
| 90° | 1 | 0 | ∞ |
사진1
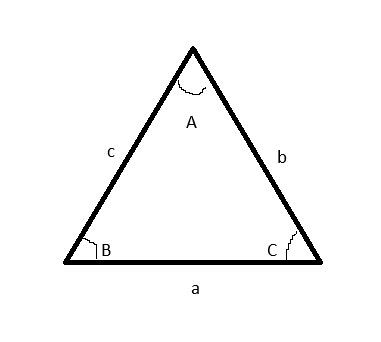
사인법칙(사진1 참조)
sinAa=sinBb=sinCc
코사인법칙(사진1 참조)
c2=a2+b2−2abcosC
역삼각함수
정의: (직각)삼각형의 변의 길이로 각도를 구하는 것
1. θ=arcsin빗변높이
- 정의역은 [−1,1]이며, 출력값(각도)은 −π/2에서 π/2 사이
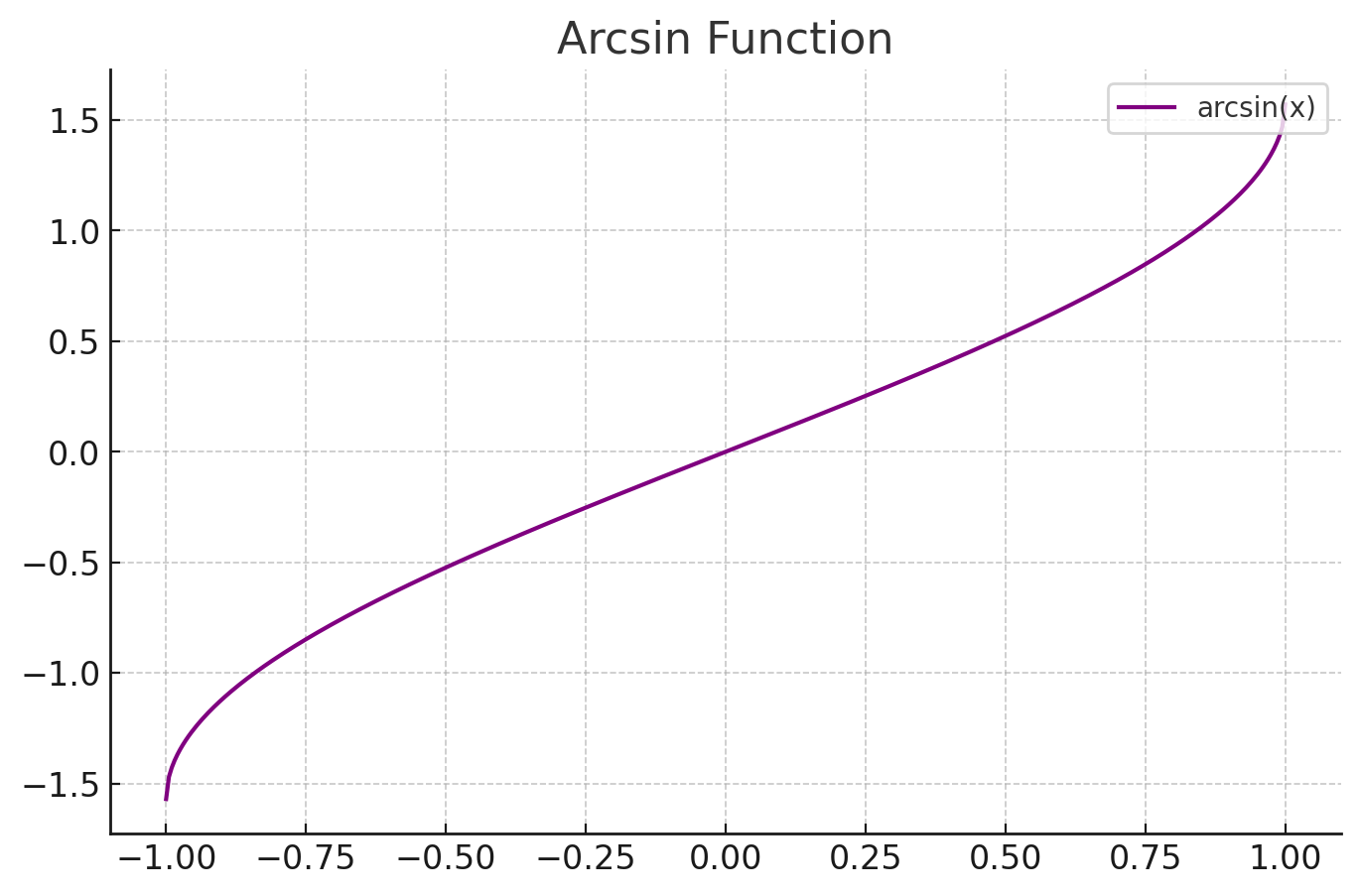
- θ=arccos빗변밑변
- 정의역은 [−1,1]이고, 출력값은 0에서 π 사이
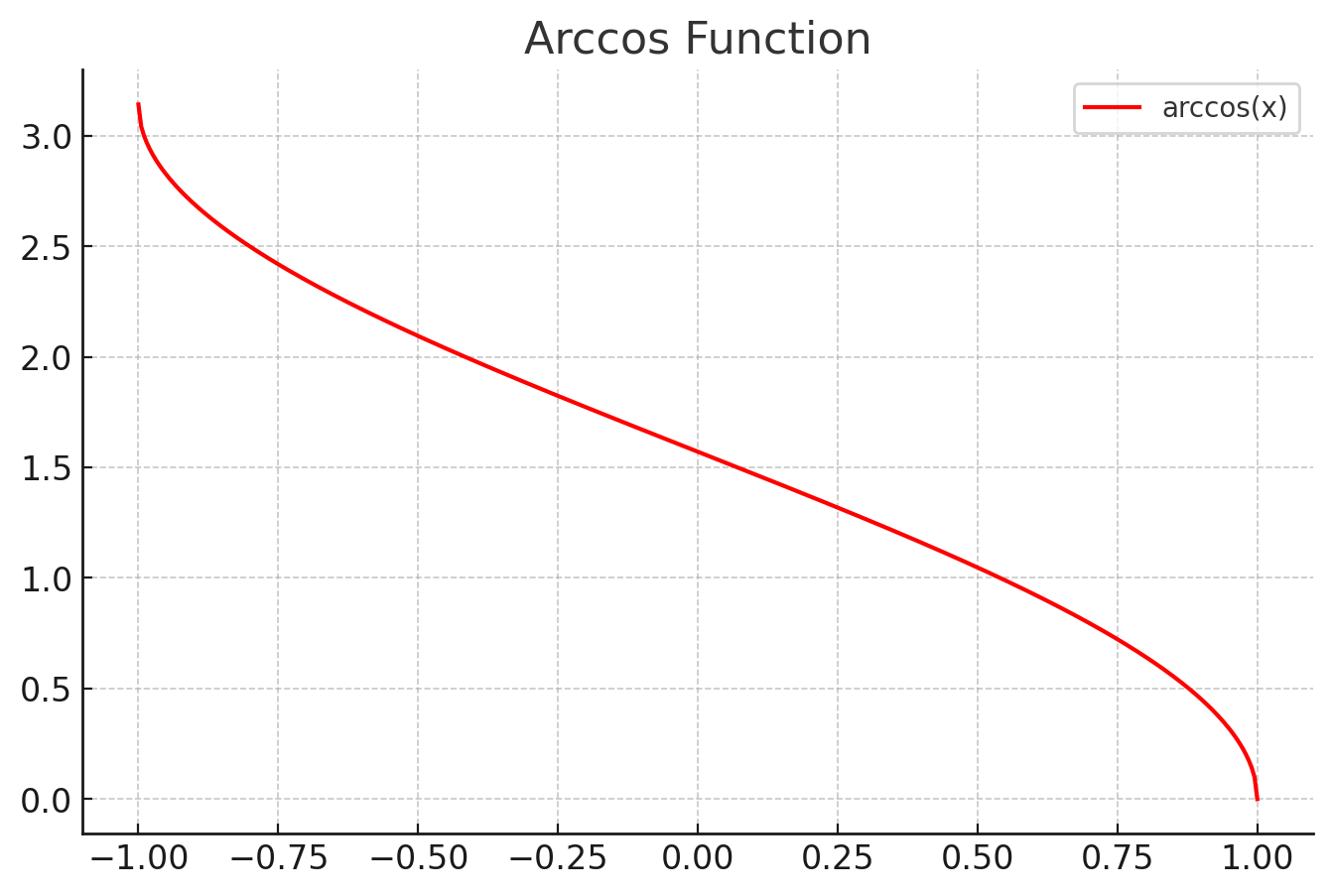
- θ=arctan밑변높이
- 정의역은 모든 실수이며, 출력값은 −π/2에서 π/2 사이로 제한
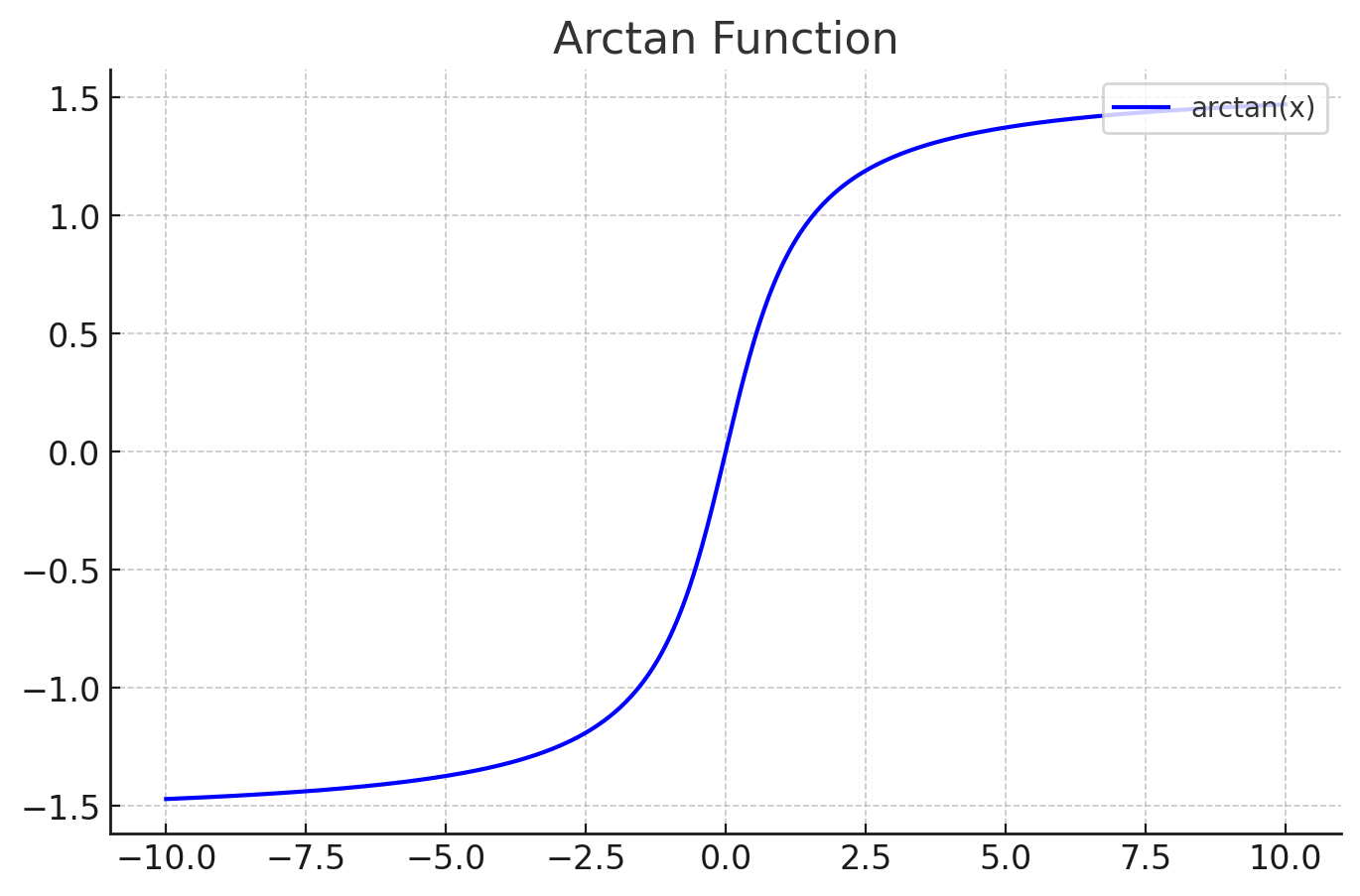
어디서 사용될까?
1. 2D 캐릭터 회전과 방향 계산
- 2D 슈팅 게임에서 플레이어가 마우스로 클릭한 방향을 계산
θ=arctan2(Δy,Δx)
- Δy와 Δx는 캐릭터와 마우스 위치의 y, x 차이
- (0, 0)에서 (Δx,Δy)까지 선을 그어서 나온 각도가 θ
라디안=θ×180π
ex: 90도 = 2π
2. 투사체의 궤적 계산
- 포탄이 발사되는 포물선(앵그리버드)
x(t)=v∗cos(θ)∗t
y(t)=v∗sin(θ)∗t−21gt2
v = 초기속도, g = 중력, t = 시간
ps: 공기저항은 계산 안했음
3. 3D 회전
- 3D에서 특정 점의 좌표값을 계산
x=r∗cos(θ)∗cos(ϕ)
y=r∗sin(ϕ)
z=r∗sin(θ)∗cos(ϕ)
r: 반지름, θ: 수평 회전 각도, ϕ: 수직 회전 각도
4. 거리계산
- 피타고라스!
a2+b2=c2
Δx2+Δy2=거리
등이 있다.






