완전 탐색 (Brute Force)

가능한 모든 경우의 수를 전부 시도하여 답을 찾는 방법입니다.
모든 조합이나 순열을 일일이 확인하기 때문에 단순하지만, 작은 입력 크기에서는 유용하지만 입력 크기가 크다면 계산량이 많아질 수 있습니다.

예제: 4자리 비밀번호를 찾아라.

이 문제를 완전 탐색(Brute Force) 방식으로 해결하고자 할 때,
0000부터 9999까지 모든 숫자를 순차적으로 대입하며 조건을 검사합니다.

모든 후보를 하나씩 확인하면서 조건에 맞는 비밀번호를 찾아내는 방식입니다.

코드

#include <iostream>
#include <iomanip> // setw, setfill
#include <random> // 난수 생성

int main() {
	std::random_device rd; // 하드웨어 또는 OS 기반의 진짜 무작위 값(seed)을 얻기 위한 객체
	std::mt19937 gen(rd()); // gen은 난수 "엔진" 역할, 난수 엔진 초기화

	std::uniform_int_distribution<> dis(0, 9999); // 0 ~ 9999로 분포 범위 지정

	int key = dis(gen); // 0 ~ 9999 사이 난수 생성

	for (int i = 0; i < 10000; ++i) {
		if (key == i) {
			std::cout << "비밀번호 : " << std::setw(4) << std::setfill('0') << i;
            // setw(4) : 출력될 자릿수를 4자리로 고정
            // setfill('0') : setw()로 지정한 자릿수보다 출력할 값이 짧을 경우, 남는 앞자리를 '0'으로 채움
			break;
		}
	}

	return 0;
}

결과

임의의 섬에서 출발해 모든 섬을 정확히 한 번씩만 방문하는 경로 중 최소 비용을 구하시오.

이 문제를 완전 탐색(Brute Force) 방식으로 해결한다고 할 때,
섬의 개수가 $n$개라면, 가능한 경로의 수는 $𝑛!$ 가지입니다.
각 섬의 방문 순서를 순열로 생성해, 각 경로의 비용을 계산하여 그중 최소 비용을 선택하는 방식입니다.

예제: 4개의 섬과 경로 비용

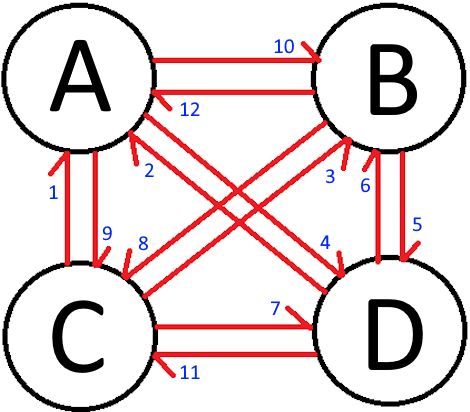
아래는 섬이 4개일 때 가능한 모든 경로와 각각의 이동 비용을 정리한 예입니다.

A → B → C → D : 25
A → B → D → C : 26
A → C → B → D : 17
A → C → D → B : 22
A → D → B → C : 18
A → D → C → B : 18
B → A → C → D : 28
B → A → D → C : 27
B → C → A → D : 13
B → C → D → A : 17
B → D → A → C : 16
B → D → C → A : 17
C → A → B → D : 16
C → A → D → B : 11
C → B → A → D : 19
C → B → D → A : 10
C → D → A → B : 19
C → D → B → A : 25
D → A → B → C : 20
D → A → C → B : 14
D → B → A → C : 27
D → B → C → A : 15
D → C → A → B : 22
D → C → B → A : 26

코드 | DFS + Backtracking

#include <iostream>
#include <vector>
#include <climits> // INT_MAX

using namespace std;

vector<vector<int>> weight; // 비용
vector<bool> visited; // 방문 여부
vector<int> path; // 현재 경로

int n; // 섬의 개수
int minCost = INT_MAX; // 최소 비용

void dfs(int cost) {
	 if (cost >= minCost) return; // 가지치기
	
    if (path.size() == n) {
        if (cost < minCost) minCost = cost;

        return;
    }

    for (int i = 0; i < n; ++i) {
        if (visited[i] == true) continue;

        int addedCost = path.empty() ? 0 : weight[path.back()][i]; 
		// 현재 경로 마지막 섬에서 새로 방문하는 섬까지의 이동 비용, 처음 방문할 때는 0
        
        visited[i] = true;
        path.push_back(i);

        dfs(cost + addedCost);

        // 백트래킹
        path.pop_back();
        visited[i] = false;
    }
}

int main() {
    weight = {
        {0, 10, 9, 4},
        {12, 0, 8, 5},
        {1, 3, 0, 7},
        {2, 6, 11, 0}
    };

    n = weight.size();
    minCost = INT_MAX;

    visited.assign(n, false);
    path.clear();

    dfs(0);

    cout << "최소 비용: " << minCost;

    return 0;
}

결과