데이크스트라 알고리즘 (Dijkstra algorithm)
가중치가 음수가 아닌 그래프에서 한 정점으로부터 다른 모든 정점까지의 최단 경로를 찾는 알고리즘입니다.
이 알고리즘은 내비게이션 앱에서 가장 빠른 길을 찾거나, 네트워크에서 데이터 패킷이 전송될 최적의 경로를 결정하는 A* 알고리즘의 기초가 됩니다.
에츠허르 데이크스트라(Edsger W. Dijkstra)가 개발한 알고리즘으로, 다익스트라 알고리즘 이라고도 불립니다.
또한, 데이크스트라 알고리즘(Dijkstra algorithm)은 매 순간 최적이라고 생각되는 선택을 하는 알고리즘인 탐욕법(Greedy algorithm) 중 하나입니다.
Dijkstra algorithm의 핵심 요소
1. 출발점 설정: 출발 정점의 최단 거리를 0으로 설정하고, 나머지 모든 정점의 최단 거리는 무한대로 설정합니다.
2. 가장 가까운 정점 선택: 아직 방문하지 않은 정점들 중에서 출발 정점으로부터의 최단 거리가 가장 짧은 정점을 선택합니다.
3. 거리 업데이트: 선택된 정점을 거쳐서 갈 수 있는 주변 정점들의 거리를 계산합니다. 만약 기존에 알려진 거리보다 더 짧은 경로가 발견되면, 해당 정점의 최단 거리를 업데이트합니다.
4. 반복: 모든 정점을 방문할 때까지 이 과정을 반복합니다. 각 단계에서 방문하는 정점은 출발점으로부터 그 시점까지 가장 가까운 정점이므로, 최종적으로 모든 정점까지의 최단 경로를 보장하게 됩니다.
구현
그래프
인접 행렬을 통해 양방향 그래프 구조를 그려줍니다.
const int INF = std::numeric_limits<int>::max(); // 무한대(Infinity)
int main() {
std::vector<std::vector<int>> graph = {
{0, 4, INF, INF, INF, 10},
{4, 0, 8, 1, INF, 5},
{INF, 8, 0, 7, 2, INF},
{INF, 1, 7, 0, 9, 3},
{INF, INF, 2, 9, 0, 6},
{10, 5, INF, 3, 6, 0}
};
return 0;
}아래의 그림처럼 양방향 그래프가 생성되었습니다.
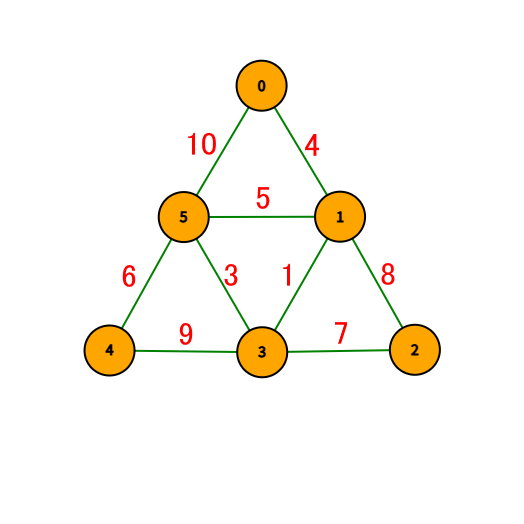
전체 코드
#include <iostream>
#include <vector>
#include <queue>
#include <limits>
#include <string>
const int INF = std::numeric_limits<int>::max();
void dijkstra(const std::vector<std::vector<int>>& graph, int start) {
int num_nodes = graph.size();
std::vector<int> dist(num_nodes, INF); // 출발점으로부터의 최단 거리를 저장하는 배열
std::vector<bool> visited(num_nodes, false);
dist[start] = 0;
for (int i = 0; i < num_nodes; ++i) {
// 1. 방문하지 않은 정점 중 가장 거리가 짧은 정점 찾기
int min_dist = INF;
int u = -1;
for (int v = 0; v < num_nodes; ++v) {
if (!visited[v] && dist[v] < min_dist) {
min_dist = dist[v];
u = v;
}
}
if (u == -1) break; // 더 이상 도달 가능한 정점이 없으면 종료
visited[u] = true; // 가장 짧은 정점을 방문 처리
// 2. 선택된 정점을 통해 다른 정점들의 거리 갱신
for (int v = 0; v < num_nodes; ++v) {
if (!visited[v] && graph[u][v] != INF) {
if (dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v]; // 더 짧은 경로가 발견되면 갱신
}
}
}
}
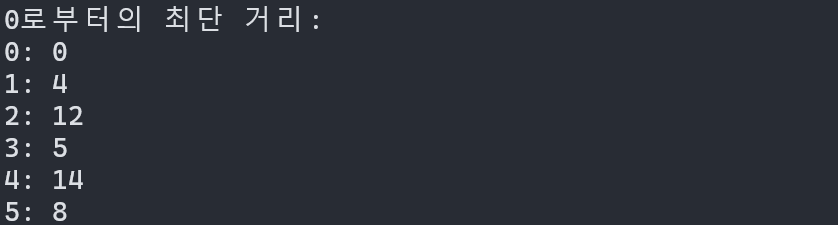
std::cout << start << "로부터의 최단 거리: " << std::endl;
for (int i = 0; i < num_nodes; ++i) {
std::cout << i << ": " << dist[i] << std::endl;
}
}
int main() {
std::vector<std::vector<int>> graph = {
{0, 4, INF, INF, INF, 10},
{4, 0, 8, 1, INF, 5},
{INF, 8, 0, 7, 2, INF},
{INF, 1, 7, 0, 9, 3},
{INF, INF, 2, 9, 0, 6},
{10, 5, INF, 3, 6, 0}
};
int start_node = 0; // 출발점 (정점 0)
dijkstra(graph, start_node);
return 0;
}
로직으로 보기
1. 초기화:
출발점인 노드 0의 최단 거리를 0으로 설정하고, 나머지 모든 정점은 무한대(INF)로 설정합니다.
- dist 배열: [0, INF, INF, INF, INF, INF]
- visited 배열: [F, F, F, F, F, F] (모든 노드를 아직 방문하지 않음)
2. 첫 번째 정점 선택 및 갱신:
visited가 false인 노드 중 가장 거리가 짧은 노드(0)를 선택합니다.
노드(0)의 visited를 true로 변경합니다.
노드(0)을 거쳐서 갈 수 있는 노드들의 거리를 계산합니다. (visited가 true인 것은 제외)
노드(1): 기존 INF > dist[0] + 4 (0 + 4 = 4)이므로 dist[1]을 4로 갱신
노드(5): 기존 INF > dist[0] + 10 (0 + 10 = 10)이므로 dist[5]를 10으로 갱신
- dist 배열: [0, 4, INF, INF, INF, 10] (노드 0에서 직접 연결된 노드 1, 5의 거리 갱신)
- visited 배열 : [T, F, F, F, F, F]
3. 두 번째 정점 선택 및 갱신:
visited가 false인 노드 중 가장 거리가 짧은 노드(1)를 선택합니다.
노드(1)의 visited를 true로 변경합니다.
노드(1)을 거쳐서 갈 수 있는 노드들의 거리를 계산합니다. (visited가 true인 것은 제외)
노드(2): 기존 INF > dist[1] + 8 (4 + 8 = 12)이므로 dist[2]를 12로 갱신.
노드(3): 기존 INF > dist[1] + 1 (4 + 1 = 5)이므로 dist[3]을 5로 갱신.
노드(5): 기존 10 > dist[1] + 5 (4 + 5 = 9)이므로 dist[5]를 9로 갱신.
- dist 배열: [0, 4, 12, 5, INF, 9]
- visited 배열: [T, T, F, F, F, F]
4. 세 번째 정점 선택 및 갱신:
visited가 false인 노드 중 가장 거리가 짧은 노드(3)를 선택합니다.
노드(3)의 visited를 true로 변경합니다.
노드(3)을 거쳐서 갈 수 있는 노드들의 거리를 계산하여 갱신합니다. (visited가 true인 것은 제외)
노드(2): 기존 12 > dist[3] + 7 (5 + 7 = 12)이므로 갱신하지 않음.
노드(4): 기존 INF > dist[3] + 9 (5 + 9 = 14)이므로 dist[4]를 14로 갱신.
노드(5): 기존 9 > dist[3] + 3 (5 + 3 = 8)이므로 dist[5]를 8로 갱신.
- dist 배열: [0, 4, 12, 5, 14, 8]
- visited 배열: [T, T, F, T, F, F]
5. 네 번째 정점 선택 및 갱신:
visited가 false인 노드 중 가장 거리가 짧은 노드(5)를 선택합니다.
노드(5)의 visited를 true로 변경합니다.
노드(5)를 거쳐서 갈 수 있는 노드들의 거리를 갱신합니다. (visited가 true인 것은 제외)
노드(4): 기존 14 > dist[5] + 6 (8 + 6 = 14)이므로 갱신하지 않음.
- dist 배열: [0, 4, 12, 5, 14, 8]
- visited 배열: [T, T, F, T, F, T]
6. 다섯 번째 정점 선택 및 갱신:
visited가 false인 노드 중 가장 거리가 짧은 노드(2)를 선택합니다.
노드(2)의 visited를 true로 변경합니다.
노드(2)를 거쳐서 갈 수 있는 노드들의 거리를 갱신합니다. (visited가 true인 것은 제외)
없음.
- dist 배열: [0, 4, 12, 5, 14, 8]
- visited 배열: [T, T, T, T, F, T]
7. 여섯 번째 정점 선택 및 갱신:
visited가 false인 노드 중 가장 거리가 짧은 노드(4)를 선택합니다.
노드(4)의 visited를 true로 변경합니다.
노드(4)를 거쳐서 갈 수 있는 노드들의 거리를 갱신합니다. (visited가 true인 것은 제외)
없음.
- dist 배열: [0, 4, 12, 5, 14, 8]
- visited 배열: [T, T, T, T, T, T]
8. 종료:
dist 배열을 출력합니다.
