자료구조

배열(Array)

배열은 동일한 타입의 요소들이 연속된 메모리 공간에 저장되는 자료구조이다. 배열의 장점은 인덱스를 통해 요소에 빠르게 접근할 수 있다는 점이며 단점은 크기가 고정되어 있어 크기를 변경할 수 없다는 점이다.

배열 예제

arr = [1, 2, 3, 4, 5]
print(arr[2])

연결 리스트 (Linked List)

연결리스트는 각 요소가 노드로 구성되며 각 노드는 데이터와 다음 노드를 가리키는 포인터를 포함한다. 연결 리스트는 요소 삽입과 삭제가 용이하지만 임의의 인덱스로 접근하는 데 시간이 많이 소요된다.

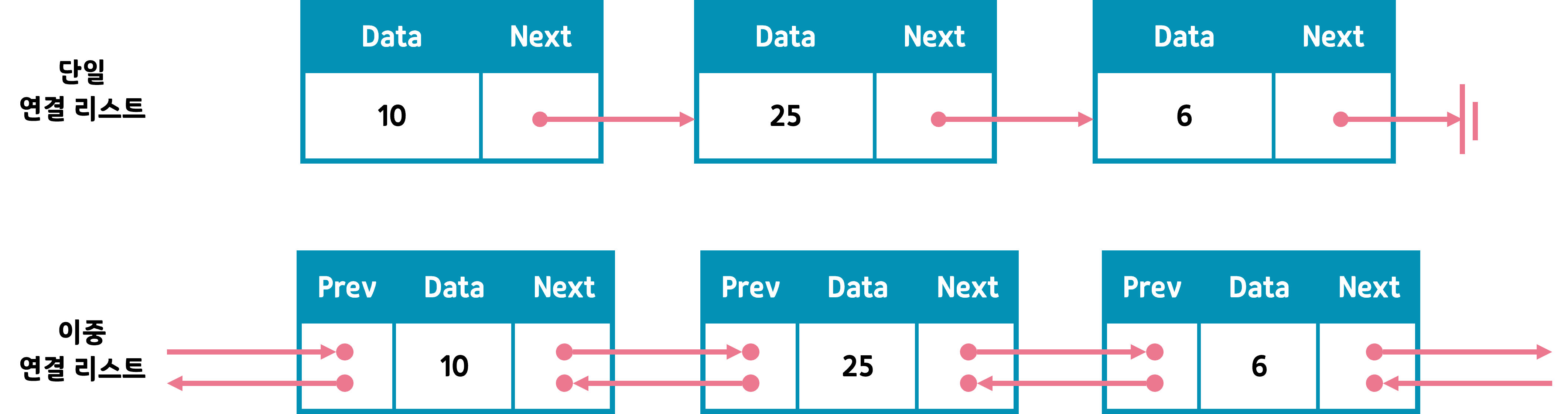
단일 연결 리스트 (Singly Linked List)

단일 연결 리스트는 각 노드가 다음 노드로의 링크를 포함한다.

단일 연결 리스트 예제

class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None

class SinglyLinkedList:
    def __init__(self):
        self.head = None

    def append(self, data):
        new_node = Node(data)
        if self.head is None:
            self.head = new_node
            return
        last = self.head
        while last.next:
            last = last.next
        last.next = new_node

    def display(self):
        current = self.head
        while current:
            print(current.data, end=" -> ")
            current = current.next
        print(None)

# 사용 예제
sll = SinglyLinkedList()
sll.append(1)
sll.append(2)
sll.append(3)
sll.display()  # 출력: 1 -> 2 -> 3 -> None

이중 연결 리스트 (Doubly Linked List)

이중 연결 리스트는 각 노드가 다음 노드와 이전 노드로의 링크를 포함한다.

이중 연결 리스트 예제

class Node:
    def __init__(self, data=None):
        self.data = data
        self.next = None
        self.prev = None

class DoublyLinkedList:
    def __init__(self):
        self.head = None

    def append(self, data):
        new_node = Node(data)
        if self.head is None:
            self.head = new_node
            return
        last = self.head
        while last.next:
            last = last.next
        last.next = new_node
        new_node.prev = last

    def display(self):
        current = self.head
        while current:
            print(current.data, end=" <-> ")
            current = current.next
        print(None)

# 사용 예제
dll = DoublyLinkedList()
dll.append(1)
dll.append(2)
dll.append(3)
dll.display()  # 출력: 1 <-> 2 <-> 3 <-> None

스택 (Stack)

스택은 LIFO(Last In First Out) 방식으로 동작하는 자료구조이다. 스택은 요소의 push, pop 연산이 주요 연산이다.

스택 예제

class Stack:
    def __init__(self):
        self.items = []

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if not self.is_empty():
            return self.items.pop()
        return None

    def peek(self):
        if not self.is_empty():
            return self.items[-1]
        return None

    def is_empty(self):
        return len(self.items) == 0

# 사용 예제
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
print(stack.pop())  # 출력: 3
print(stack.peek())  # 출력: 2

큐(Queue)

큐는 FIFO(First In First Out) 방식으로 동작하는 자료구조이다. 큐는 요소의 enqueue와 dequeue 연산이 주요 연산이다.

큐 예제

class Stack:
    def __init__(self):
        self.items = []

    def push(self, item):
        self.items.append(item)

    def pop(self):
        if not self.is_empty():
            return self.items.pop()
        return None

    def peek(self):
        if not self.is_empty():
            return self.items[-1]
        return None

    def is_empty(self):
        return len(self.items) == 0

# 사용 예제
stack = Stack()
stack.push(1)
stack.push(2)
stack.push(3)
print(stack.pop())  # 출력: 3
print(stack.peek())  # 출력: 2

해시 테이블 (Hash Table)

해시 테이블은 key-value 쌍을 저장하는 자료구조이다. 해시 함수를 사용하여 key를 인덱스로 변환하여 값을 저장하고 검색한다.

해시 테이블 예제

class HashTable:
    def __init__(self, size):
        self.size = size
        self.table = [None] * size

    def hash_function(self, key):
        return hash(key) % self.size

    def insert(self, key, value):
        index = self.hash_function(key)
        self.table[index] = value

    def get(self, key):
        index = self.hash_function(key)
        return self.table[index]

# 사용 예제
hash_table = HashTable(10)
hash_table.insert('name', 'Alice')
print(hash_table.get('name'))  # 출력: Alice

트리 (Tree)

트리는 계층적인 구조를 가지는 비선형 자료구조이다. 트리는 루트 노드와 자식 노드로 구성되며 각 노드는 여러개의 자식노드를 가질 수 있다.

• 노드(Node): 트리의 기본 구성 요소로, 데이터를 저장하는 단위다.
• 루트 노드(Root Node): 트리의 최상위 노드이니다. 트리는 하나의 루트 노드를 가진다.
• 자식 노드(Child Node): 특정 노드의 하위 노드이다.
• 부모 노드(Parent Node): 특정 노드의 상위 노드이다.
• 형제 노드(Sibling Node): 동일한 부모를 공유하는 노드들이다.
• 잎 노드(Leaf Node): 자식 노드가 없는 노드이다.
• 가지 노드(Internal Node): 자식 노드를 가진 노드이다.
• 트리의 높이(Height of Tree): 루트 노드에서 가장 깊은 잎 노드까지의 경로 길이이다.
• 레벨(Level): 루트 노드를 레벨 0으로 할 때, 특정 노드의 깊이를 나타낸다.

이진 트리 (Binary Tree)

이진 트리는 각 노드가 두개의 자식 노드를 가진다.

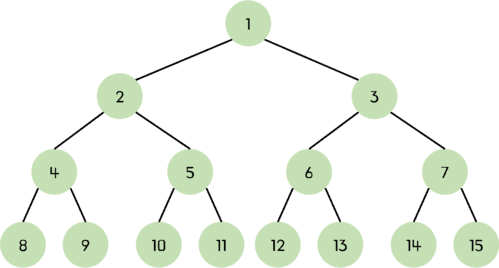
이진 트리 예제

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def inorder_traversal(root):
    if root:
        inorder_traversal(root.left)
        print(root.value, end=" ")
        inorder_traversal(root.right)

# 사용 예제
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
inorder_traversal(root)  # 출력: 2 1 3

이진 탐색 트리 (Binary Search Tree, BST)

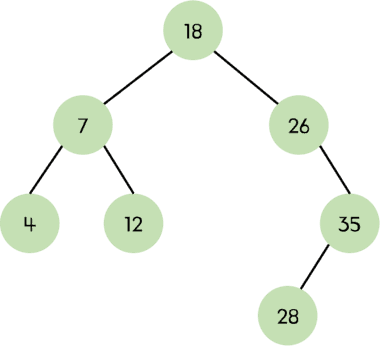
이진 탐색 트리는 이진 트리의 일종으로 각 노드가 특정한 순서에 따라 배치되는 트리이다. 왼쪽 서브트리의 모든 값은 루트 노드의 값보다 작고 오른쪽 서브트리의 모든 값은 루트 노드의 값보다 크다.

이진 탐색 트리 예제

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

class BinarySearchTree:
    def __init__(self):
        self.root = None

    def insert(self, value):
        new_node = TreeNode(value)
        if self.root is None:
            self.root = new_node
            return
        current = self.root
        while True:
            if value < current.value:
                if current.left is None:
                    current.left = new_node
                    return
                current = current.left
            else:
                if current.right is None:
                    current.right = new_node
                    return
                current = current.right

    def inorder_traversal(self, root):
        if root:
            self.inorder_traversal(root.left)
            print(root.value, end=" ")
            self.inorder_traversal(root.right)

# 사용 예제
bst = BinarySearchTree()
bst.insert(10)
bst.insert(5)
bst.insert(15)
bst.inorder_traversal(bst.root)  # 출력: 5 10 15

그래프 (graph)

그래프는 정점(Vertex)과 간선(Edge)으로 구성된 자료구조로, 다양한 문제를 모델링하고 해결하는 데 사용된다. 네트워크, 지도, 소셜 네트워크 분석 등에서 그래프가 활용된다. 그래프는 크게 방향 그래프(Directed Graph)와 무방향 그래프(Undirected Graph)로 나눌 수 있습니다.

방향 그래프 (Directed Graph)

방향 그래프는 간선에 방향이 있는 그래프이다. 간선이 한쪽 방향으로만 연결되며 한 정점에서 다른 정점으로 이동할 수 있는 방향이 정해져 있다. 이를 화살표로 표현하며 간선 (u, v)는 정점 u에서 정점 v로의 경로를 나타낸다.

방향 그래프 예제

class DirectedGraph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, u, v):
        if u not in self.graph:
            self.graph[u] = []
        self.graph[u].append(v)

    def print_graph(self):
        for key in self.graph:
            print(f"{key}: {self.graph[key]}")

# 사용 예제
dg = DirectedGraph()
dg.add_edge(0, 1)
dg.add_edge(0, 2)
dg.add_edge(1, 2)
dg.add_edge(2, 0)
dg.add_edge(2, 3)
dg.add_edge(3, 3)
dg.print_graph()
# 출력:
# 0: [1, 2]
# 1: [2]
# 2: [0, 3]
# 3: [3]

무방향 그래프 (Undirected Graph)

무방향 그래프는 간선에 방향이 없는 그래프이다. 간선이 양방향으로 연결되며 정점 u에서 정점 v로 가는 경로와 정점 v에서 정점 u로 가는 경로가 동일합니다. 간선 (u, v)는 정점 u와 정점 v가 서로 연결되어 있음을 나낸다.

무방향 그래프 예제

class UndirectedGraph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, u, v):
        if u not in self.graph:
            self.graph[u] = []
        if v not in self.graph:
            self.graph[v] = []
        self.graph[u].append(v)
        self.graph[v].append(u)

    def print_graph(self):
        for key in self.graph:
            print(f"{key}: {self.graph[key]}")

# 사용 예제
ug = UndirectedGraph()
ug.add_edge(0, 1)
ug.add_edge(0, 2)
ug.add_edge(1, 2)
ug.add_edge(2, 3)
ug.print_graph()
# 출력:
# 0: [1, 2]
# 1: [0, 2]
# 2: [0, 1, 3]
# 3: [2]

가중치 그래프 (Weighted Graph)

가중치 그래프는 간선에 가중치(Weight)가 부여된 그래프이다. 가중치는 두 정점을 연결하는 간선의 비용, 거리 시간 등을 나타낼 수 있으며 네트워크의 최단 경로 문제, 최소 비용 신장 트리 등 다양한 문제를 해결하는 데 사용된다.

가중치 그래프 예제

class WeightedGraphMatrix:
    def __init__(self, vertices):
        self.vertices = vertices
        self.graph = [[float('inf')] * vertices for _ in range(vertices)]

    def add_edge(self, u, v, weight):
        self.graph[u][v] = weight
        self.graph[v][u] = weight  # 무방향 그래프의 경우

    def print_graph(self):
        for row in self.graph:
            print(row)

# 사용 예제
g = WeightedGraphMatrix(4)
g.add_edge(0, 1, 1)
g.add_edge(0, 2, 4)
g.add_edge(1, 2, 2)
g.add_edge(2, 3, 3)
g.print_graph()
# 출력:
# [inf, 1, 4, inf]
# [1, inf, 2, inf]
# [4, 2, inf, 3]
# [inf, inf, 3, inf]

연결 그래프 (Connected Graph)

연결 그래프는 그래프의 모든 정점이 서로 연결되어 있는 그래프이다. 어떤 두 정점 사이에도 경로가 존재한다. 방향 그래프의 경우, 모든 정점 간에 양방향 경로가 존재할 때 이를 강하게 연결된 그래프(Strongly Connected Graph)라고 합니다.

연결 그래프 예제

class ConnectedGraph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, u, v):
        if u not in self.graph:
            self.graph[u] = []
        if v not in self.graph:
            self.graph[v] = []
        self.graph[u].append(v)
        self.graph[v].append(u)  # 무방향 그래프의 경우

    def is_connected(self):
        visited = set()
        self.dfs(next(iter(self.graph)), visited)
        return len(visited) == len(self.graph)

    def dfs(self, v, visited):
        visited.add(v)
        for neighbor in self.graph[v]:
            if neighbor not in visited:
                self.dfs(neighbor, visited)

# 사용 예제
g = ConnectedGraph()
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 2)
g.add_edge(2, 3)
print(g.is_connected())  # 출력: True

비연결 그래프 (Disconnected Graph)

비연결 그래프는 일부 정점 사이에 경로가 없는 그래프이다. 어떤 두 정점 사이에도 경로가 존재하지 않는 경우가 있으며 여러 개의 연결 성분(Connected Component)으로 나눌 수 있습니다. 각 연결 성분은 연결된 부분 그래프이다.

class DisconnectedGraph:
    def __init__(self):
        self.graph = {}

    def add_edge(self, u, v):
        if u not in self.graph:
            self.graph[u] = []
        if v not in self.graph:
            self.graph[v] = []
        self.graph[u].append(v)
        self.graph[v].append(u)  # 무방향 그래프의 경우

    def is_connected(self):
        visited = set()
        self.dfs(next(iter(self.graph)), visited)
        return len(visited) == len(self.graph)

    def dfs(self, v, visited):
        visited.add(v)
        for neighbor in self.graph[v]:
            if neighbor not in visited:
                self.dfs(neighbor, visited)

    def find_connected_components(self):
        visited = set()
        components = []
        for vertex in self.graph:
            if vertex not in visited:
                component = []
                self.dfs_collect(vertex, visited, component)
                components.append(component)
        return components

    def dfs_collect(self, v, visited, component):
        visited.add(v)
        component.append(v)
        for neighbor in self.graph[v]:
            if neighbor not in visited:
                self.dfs_collect(neighbor, visited, component)

# 사용 예제
g = DisconnectedGraph()
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(3, 4)
print(g.is_connected())  # 출력: False
print(g.find_connected_components())  # 출력: [[0, 1, 2], [3, 4]]

heapq

파이썬에서 heap 자료구조를 구현한 모듈로 최소 힙을 기본으로 제공한다. heap은 이진 트리 형태의 완전 이진 트리로 구현되며 부모 노드는 항상 자식 노드보다 작거나 같은 값을 가진다.

heapq 주요 함수

heapq.heappush(heap, item)

• 힙에 새로운 요소를 추가한다.
• 시간 복잡도: O(log n)

heapq.heappop(heap):

• 힙에서 가장 작은 요소를 제거하고 반환한다.
• 시간 복잡도: O(log n)
  

heapq.heappushpop(heap, item):

• 힙에 새로운 요소를 추가한 후, 가장 작은 요소를 제거하고 반환한다.
• 시간 복잡도: O(log n)

heapq.heapreplace(heap, item):

• 힙의 루트 요소를 제거하고, 새로운 요소를 추가한다.
• 시간 복잡도: O(log n)

heapq.heapify(iterable):

• 리스트를 힙으로 변환합니다.
• 시간 복잡도: O(n)

heapq.nlargest(n, iterable, key=None):

• iterable에서 가장 큰 n개의 요소를 반환합니다.
• 시간 복잡도: O(n log n)

heapq.nsmallest(n, iterable, key=None):

• iterable에서 가장 작은 n개의 요소를 반환합니다.
• 시간 복잡도: O(n log n)

heapq 예제

import heapq

# 최소 힙 예제
min_heap = []
heapq.heappush(min_heap, 3)
heapq.heappush(min_heap, 1)
heapq.heappush(min_heap, 4)
heapq.heappush(min_heap, 1)
heapq.heappush(min_heap, 5)
heapq.heappush(min_heap, 9)

print("Min-Heap:", min_heap)
print("Pop:", heapq.heappop(min_heap))  # 가장 작은 요소 반환 및 제거
print("Min-Heap after pop:", min_heap)

# 기존 리스트를 힙으로 변환
data = [1, 3, 5, 7, 9, 2, 4, 6, 8, 0]
heapq.heapify(data)
print("Heapified list:", data)

# 최대 힙 예제 (음수 값으로 변환하여 사용)
max_heap = []
heapq.heappush(max_heap, -3)
heapq.heappush(max_heap, -1)
heapq.heappush(max_heap, -4)
heapq.heappush(max_heap, -1)
heapq.heappush(max_heap, -5)
heapq.heappush(max_heap, -9)

print("Max-Heap:", [-x for x in max_heap])
print("Pop:", -heapq.heappop(max_heap))  # 가장 큰 요소 반환 및 제거
print("Max-Heap after pop:", [-x for x in max_heap])

# nlargest와 nsmallest 사용 예제
print("3 largest elements:", heapq.nlargest(3, data))
print("3 smallest elements:", heapq.nsmallest(3, data))

heapq를 이용한 우선순위 큐

import heapq

class PriorityQueue:
    def __init__(self):
        self.heap = []

    def push(self, priority, item):
        heapq.heappush(self.heap, (priority, item))

    def pop(self):
        return heapq.heappop(self.heap)[1]

# 사용 예제
pq = PriorityQueue()
pq.push(3, "task 3")
pq.push(1, "task 1")
pq.push(2, "task 2")

print("Pop:", pq.pop())  # 출력: task 1
print("Pop:", pq.pop())  # 출력: task 2
print("Pop:", pq.pop())  # 출력: task 3

알고리즘

완전탐색 (Brute Force Algorithm)

완전 탐색 알고리즘은 가능한 모든 경우의 수를 하나씩 모두 탐색하여 문제의 해를 찾는 방법으로 문제를 해결하는 가장 직관적이고 간단한 방법이지만 일반적으로 시간 복잡도가 높기 때문에 입력의 크기가 작은 경우에만 실용적이다.

완전 탐색을 사용하는 대표적인 문제

1. 순열(Permutation): 주어진 집합의 모든 순열을 생성하는 문제.

itertools를 활용한 순열 생성 예제

from itertools import permutations

data = [1, 2, 3]
perm = permutations(data)

for p in perm:
    print(p)
# 출력:
# (1, 2, 3)
# (1, 3, 2)
# (2, 1, 3)
# (2, 3, 1)
# (3, 1, 2)
# (3, 2, 1)

순열 직접 구현 예제

def permutations(arr):
    result = []
    if len(arr) == 1:
        return [arr]
    for i in range(len(arr)):
        rest = arr[:i] + arr[i+1:]
        for p in permutations(rest):
            result.append([arr[i]] + p)
    return result

# 사용 예제
data = [1, 2, 3]
perm = permutations(data)
for p in perm:
    print(p)
# 출력:
# [1, 2, 3]
# [1, 3, 2]
# [2, 1, 3]
# [2, 3, 1]
# [3, 1, 2]
# [3, 2, 1]

2. 조합(Combination): 주어진 집합에서 모든 가능한 조합을 생성하는 문제.

itertools를 활용한 조합 생성 예제

from itertools import combinations

data = [1, 2, 3]
comb = combinations(data, 2)

for c in comb:
    print(c)
# 출력:
# (1, 2)
# (1, 3)
# (2, 3)

조합 직접 구현 예제

def combinations(arr, r):
    result = []
    if r == 0:
        return [[]]
    for i in range(len(arr)):
        rest = arr[i+1:]
        for c in combinations(rest, r-1):
            result.append([arr[i]] + c)
    return result

# 사용 예제
data = [1, 2, 3]
comb = combinations(data, 2)
for c in comb:
    print(c)
# 출력:
# [1, 2]
# [1, 3]
# [2, 3]

3. 부분 집합(Subsets): 주어진 집합의 모든 부분 집합을 생성하는 문제.

itertools를 활용한 부분 집합 생성 예제

from itertools import chain, combinations

def all_subsets(iterable):
    s = list(iterable)
    return chain.from_iterable(combinations(s, r) for r in range(len(s) + 1))

data = [1, 2, 3]
subsets = all_subsets(data)

for subset in subsets:
    print(subset)
# 출력:
# ()
# (1,)
# (2,)
# (3,)
# (1, 2)
# (1, 3)
# (2, 3)
# (1, 2, 3)

부분 집합 직접 구현 예제

def subsets(arr):
    result = []
    def backtrack(start, path):
        result.append(path)
        for i in range(start, len(arr)):
            backtrack(i + 1, path + [arr[i]])
    backtrack(0, [])
    return result

# 사용 예제
data = [1, 2, 3]
subsets_result = subsets(data)
for subset in subsets_result:
    print(subset)
# 출력:
# []
# [1]
# [1, 2]
# [1, 2, 3]
# [1, 3]
# [2]
# [2, 3]
# [3]

4. 배열의 합(Sum of Subarray): 배열에서 특정 조건을 만족하는 부분 배열을 찾는 문제.

배열의 합 문제 예제

def subarray_sum(arr, target):
    n = len(arr)
    for start in range(n):
        for end in range(start + 1, n + 1):
            if sum(arr[start:end]) == target:
                return arr[start:end]
    return None

arr = [1, 2, 3, 4, 5]
target = 9
result = subarray_sum(arr, target)
print(result)  # 출력: [2, 3, 4]

완전 탐색 알고리즘 시간복잡도

완전 탐색 알고리즘의 시간 복잡도는 일반적으로 매우 높다. 예를 들어 순열을 생성하는 알고리즘의 시간 복잡도는 O(n!)이고, 조합을 생성하는 알고리즘의 시간 복잡도는 O(2^n)이다. 이러한 높은 시간 복잡도 때문에 완전 탐색 알고리즘은 입력 크기가 작을 때만 실용적이다.

완전 탐색 알고리즘의 최적화

완전 탐색은 모든 가능한 경우의 수를 탐색하기 때문에 종종 비효율적이어서 다양한 최적화 기법으로 탐색 시간을 줄일 수 있다.

1. 가지치기 (Pruning)
   가지치기는 탐색 과정에서 불필요한 경로를 미리 제거하여 탐색 시간을 줄이는 기법이다.

가지치기 활용 예제 (N-Queens)

def is_safe(board, row, col):
    for i in range(col):
        if board[row][i] == 1:
            return False
    for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
        if board[i][j] == 1:
            return False
    for i, j in zip(range(row, len(board), 1), range(col, -1, -1)):
        if board[i][j] == 1:
            return False
    return True

def solve_nqueens(board, col):
    if col >= len(board):
        return True
    for i in range(len(board)):
        if is_safe(board, i, col):
            board[i][col] = 1
            if solve_nqueens(board, col + 1):
                return True
            board[i][col] = 0
    return False

def print_board(board):
    for row in board:
        print(" ".join(str(cell) for cell in row))

N = 4
board = [[0] * N for _ in range(N)]
if solve_nqueens(board, 0):
    print_board(board)
else:
    print("Solution does not exist")
# 출력:
# 0 0 1 0
# 1 0 0 0
# 0 0 0 1
# 0 1 0 0

2. 동적 계획법 (Dynamic Programming)
   동적 계획법은 문제를 작은 하위 문제로 나누고 이들의 결과를 저장하여 동일한 하위 문제를 반복적으로 해결하는 것을 피하는 기법이다.

동적 계획법 활용 예제 (피보나치 수열)

def fibonacci(n):
    if n <= 1:
        return n
    fib = [0] * (n + 1)
    fib[1] = 1
    for i in range(2, n + 1):
        fib[i] = fib[i - 1] + fib[i - 2]
    return fib[n]

# 사용 예제
print(fibonacci(10))  # 출력: 55

3. 메모이제이션(Memoization)
   메모이제이션은 이미 계산한 값을 저장하여 동일한 계산을 반복하지 않도록 하는 기법으로 동적 계획 법의 한 형태로 볼 수 있다.

메모이제이션 활용 예제 (피보나치 수열)

def fibonacci(n, memo={}):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci(n - 1, memo) + fibonacci(n - 2, memo)
    return memo[n]

# 사용 예제
print(fibonacci(10))  # 출력: 55

4. 분할 정복(Divide and Conquer)
   분할 정복은 문제를 더 작은 하위 문제로 나누어 해결한 후 이를 합쳐서 원래 문제를 해결하는 기법이다.

분할 정복 활용 예제 (병합 정렬)

def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        L = arr[:mid]
        R = arr[mid:]

        merge_sort(L)
        merge_sort(R)

        i = j = k = 0

        while i < len(L) and j < len(R):
            if L[i] < R[j]:
                arr[k] = L[i]
                i += 1
            else:
                arr[k] = R[j]
                j += 1
            k += 1

        while i < len(L):
            arr[k] = L[i]
            i += 1
            k += 1

        while j < len(R):
            arr[k] = R[j]
            j += 1
            k += 1

# 사용 예제
arr = [12, 11, 13, 5, 6, 7]
merge_sort(arr)
print(arr)  # 출력: [5, 6, 7, 11, 12, 13]

백트래킹

백트래킹은 재귀를 사용하여 가능한 모든 해를 탐색하는 알고리즘 기법이다. 가능한 해의 후보를 구축하고 조건을 만족하지 않으면 즉시 후보를 포기하는 방법으로 탐색 공간을 줄인다.

백트래킹 주요 특징

1. 상태 공간 트리 (State Space Tree)
   모든 가능한 해를 트리 형태로 표현하고 각 노드는 문제의 상태를 나타낸다.

2. 재귀 호출 (Recursive Call)
   각 단계에서 재귀적으로 문제를 해결하며 조건을 만족하지 않으면 그 경로를 포기(Prune)한다.

3. 가지치기(Pruning)
   조건을 만족하지 않는 경로를 탐색하지 않고 버려 탐색 공간을 줄인다.

백트래킹의 장단점

장점
1. 모든 가능한 해를 탐색하여 문제를 해결한다.
2. 구현이 직관적이며 이해하기 쉽다.
3. 가지치기를 통해 탐색 공간을 줄일 수 잇다.

단점
1. 경우의 수가 많을 경우 시간 복잡도가 매우 높아질 수 있다.
2. 재귀 호출로 인해 메모리 사용량이 많을 수 있다.

백트래킹 활용 예제 (부분집합 합 문제

def subset_sum(arr, target):
    result = []
    def backtrack(start, path, current_sum):
        if current_sum == target:
            result.append(path)
            return
        for i in range(start, len(arr)):
            if current_sum + arr[i] <= target:
                backtrack(i + 1, path + [arr[i]], current_sum + arr[i])
    backtrack(0, [], 0)
    return result

# 사용 예제
arr = [3, 34, 4, 12, 5, 2]
target = 9
print(subset_sum(arr, target))  # 출력: [[3, 4, 2], [4, 5]]

재귀 (Recursion)

재귀는 함수가 자기 자신을 호출하여 문제를 해결하는 프로그래밍 기법으로 복잡한 문제를 더 작은 하위 문제로 나누어 해결하는데 유용하다. 재귀는 적절한 종료 조건이 없으면 무한 루프에 빠질 수 있기 때문에 항상 종료 조건을 명확히 정의해야한다.

재귀의 주요 특징

1. 종료 조건 (Base Case)
   재귀 호출을 멈추는 조건이다. 이 조건이 충적되면 더 이상 자기 자신을 호출 하지 않는다.
2. 재귀 단계 (Recursive Case)
   함수가 자기 자신을 호출하는 단계로 문제를 더 작은 부분으로 나누어 해결한다.

재귀의 장단점

장점
1. 코드가 간결하고 이해하기 쉽다.
2. 복잡한 문제를 더 작은 하위 문제로 나눌 수 있다.

단점
1. 함수 호출이 스택에 쌓이기 때문에 메모리 사용이 많을 수 있다.
2. 반복적인 호출로 인해 비효율적일 수 있으며 시간 복잡도가 높아질 수 있다.

재귀 활용 예제 (피보나치 수열)

def factorial(n):
    if n == 0:
        return 1
    return n * factorial(n - 1)

# 사용 예제
print(factorial(5))  # 출력: 120

DFS

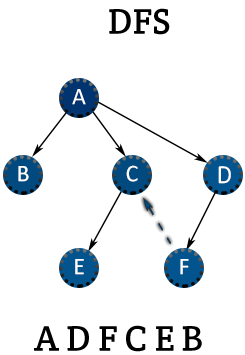
깊이 우선 탐색(DFS)는 그래프 탐색 알고리즘 중 하나로 시작 정점에서 시작하여 가능한 깊이까지 탐색한 후 더이상 갈 수 없으면 되돌아와 다른 경로를 탐색하는 방법이다. DFS는 스택 자료구조를 사용하여 구현 가능하며 재귀를 이요한 구현도 가능하다.

DFS의 특징

1. 탐색 방식 : 한 정점에서 시작하여 가능한 깊이까지 탐색한 후 더이상 갈 수 없으면 되돌아와 다른 경로를 탐색한다.
2. 자료구조 : 스택을 사용하거나 재귀 호출을 통해 구현할 수 있다.
3. 시간 복잡도 : O(V + E), (V는 정점의 수, E는 간선의 수)
4. 공간 복잡도 : O(V), (재귀 호출 스택을 사용하는 경우)

DFS의 장단점

장점
1. 구현이 간단하고 직관적이다.
2. 방문해야하는 모든 정점을 미리 저장하지 않아도 된다.
3. 깊이 있는 탐색을 통해 특정 경로를 찾는 데 유용하다.

단점
1. 종료 조건이 명확하지 않으면 무한 루프에 빠질 수 있다.
2. 재귀 호출이 깊어지면 스택 오버 플로우가 발생할 수 있다.
3. 모든 경로를 탐색하는 데 시간이 오래걸릴 수 잇다.

재귀를 이용한 DFS

def dfs_recursive(graph, vertex, visited):
    visited[vertex] = True
    print(vertex, end=' ')
    for neighbor in graph[vertex]:
        if not visited[neighbor]:
            dfs_recursive(graph, neighbor, visited)

# 사용 예제
graph = {
    0: [1, 2],
    1: [0, 3, 4],
    2: [0, 4],
    3: [1, 4],
    4: [1, 2, 3]
}
visited = [False] * len(graph)
dfs_recursive(graph, 0, visited)
# 출력: 0 1 3 4 2

스택을 이용한 DFS

def dfs_stack(graph, start):
    visited = [False] * len(graph)
    stack = [start]
    while stack:
        vertex = stack.pop()
        if not visited[vertex]:
            print(vertex, end=' ')
            visited[vertex] = True
            for neighbor in reversed(graph[vertex]):
                if not visited[neighbor]:
                    stack.append(neighbor)

# 사용 예제
graph = {
    0: [1, 2],
    1: [0, 3, 4],
    2: [0, 4],
    3: [1, 4],
    4: [1, 2, 3]
}
dfs_stack(graph, 0)
# 출력: 0 1 3 4 2

BFS

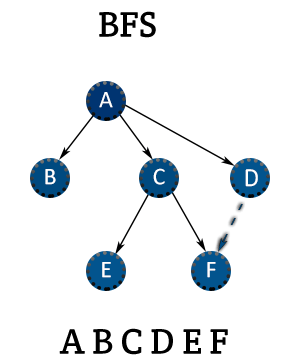
너비 우선 탐색(BFS)은 그래프 탐색 알고리즘 중 하나로 시작 정점에서 시작하여 인접한 정점을 먼저 탐색한 후 그 다음 인접한 정점들을 탐색하는 방식으로 Queue 자료 구조를 사용하여 구현할 수 있다.

BFS의 특징

1. 탐색 방식 : 시작 정점에서 인접한 정점을 먼저 탐색한 후 그 다음 인접한 정점들을 탐색한다.
2. 자료구조 : Queue를 사용하여 구현한다.
3. 시간 복잡도 : O(V + E), (V는 정점의 수, E는 간선의 수)
4. 공간 복잡도 : O(V), (Queue에 저장되는 정점의 수)

BFS 장단점

장점
1. 가중치가 없는 그래프에서 최단 경로를 찾는 데 유용하다.
2. Queue를 활용하여 간단하게 구현할 수 있다.
3. 모든 경로를 탐색하여 특정 조건을 만족하는 경로를 찾는 데 유용하다.

단점
1. Queue에 많은 정점이 저장될 수 있어 메모리 사용량이 많을 수 있다.
2. 깊이 우선 탐색(DFS)에 비해 느릴 수 있다.

BFS 구현

from collections import deque

def bfs(graph, start):
    visited = [False] * len(graph)
    queue = deque([start])
    visited[start] = True

    while queue:
        vertex = queue.popleft()
        print(vertex, end=' ')

        for neighbor in graph[vertex]:
            if not visited[neighbor]:
                queue.append(neighbor)
                visited[neighbor] = True

# 사용 예제
graph = {
    0: [1, 2],
    1: [0, 3, 4],
    2: [0, 4],
    3: [1, 4],
    4: [1, 2, 3]
}
bfs(graph, 0)
# 출력: 0 1 2 3 4

다익스트라 알고리즘 (Dijkstra's Alogrithm)

다익스트라 알고리즘은 가중치가 있는 그래프에서 단일 출발점에서 다른 모든 정점까지의 최단 경로를 찾는 알고리즘이며 음의 가중치를 가지지 않는 그래프에 적용할 수 있다.

다익스트라 알고리즘의 특징

1. 입력 : 그래프와 시작 정점
2. 출력 : 시작 정점에서 다른 모든 정점까지의 최단 경로
3. 시간복잡도 : $O(V^2)$ (V는 정점의 수), Heap(우선 순위 큐)을 사용하면 $O((V+E)logV)$ (E는 간선의 수)
4. 제약 조건 : 간선의 가중치는 음수가 아니어야 한다.

다익스트라 알고리즘의 동작 원리

1. 초기화 : 시작 정점에서 다른 모든 정점까지의 거리를 무한대로 설정하고 시작 정점의 거리는 0으로 설정한다. 우선순위 큐에 시작 정점을 삽입한다.
2. 반복 : 우선순위 큐에서 가장 거리가 짧은 정점을 추출하고 해당 정점의 인접한 정점을 검사하여 거리를 갱신한다. 갱신된 정점은 다시 우선순위 큐에 삽입한다.
3. 종료 : 우선순위 큐가 빌 때까지 반복한다.

다익스트라 알고리즘의 장단점

장점
1. Heap을 사용하면 시간 복잡도가 $O(V+2)logV)$로 효율적이다.
2. 구현이 비교적 간단하다.

단점
1. 음수 가중치를 가진 그래프에는 사용할 수 없다.
2. 단일 출발점에서 다른 모든 정점까지의 최단 경로만 계산한다.

다익스트라 알고리즘 구현

import heapq

def dijkstra(graph, start):
    # 초기화
    distances = {vertex: float('infinity') for vertex in graph}
    distances[start] = 0
    priority_queue = [(0, start)]

    while priority_queue:
        current_distance, current_vertex = heapq.heappop(priority_queue)

        # 이미 처리된 정점이면 건너뛰기
        if current_distance > distances[current_vertex]:
            continue

        for neighbor, weight in graph[current_vertex].items():
            distance = current_distance + weight

            # 최단 거리를 발견한 경우
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances

# 사용 예제
graph = {
    'A': {'B': 1, 'C': 4},
    'B': {'A': 1, 'C': 2, 'D': 5},
    'C': {'A': 4, 'B': 2, 'D': 1},
    'D': {'B': 5, 'C': 1}
}
start_vertex = 'A'
distances = dijkstra(graph, start_vertex)
print(distances)  # 출력: {'A': 0, 'B': 1, 'C': 3, 'D': 4}

two pointer

투 포인터 알고리즘은 배열이나 리스트 같은 자료구조에서 두 개의 포인터를 사용하여 문제를 해결하는 방법으로 주로 다음과 같은 경우에 유용하다.

1. 정렬된 배열에서 특정 조건을 만족하는 부분 배열 찾기
2. 두 배열에서 공통 원소 찾기
3. 회문 문자열 검사

투 포인터 알고리즘의 기본 아이디어

1. 포인터 초기화 : 두 개의 포인터를 초기화한다. 보통 하나느 시작 지점에 다른 하나는 끝 지점에 놓는다.
2. 조건 검사 및 포인터 이동 : 문제에서 요구하는 조건을 검사하고 조건에 따라 포인터를 이동시킨다.
3. 종료 조건 : 포인터가 서로 교차하거나 특정 조건을 만족할 때까지 반복한다.

투 포인터 알고리즘의 장단점

장점
1. O(n)시간 복잡도로 문제를 해결할 수 있다.
2. 구현이 비교적 간단하다.
단점
1. 일부 문제에서는 입력 배열이 정렬되어 있어야 한다.
2. 특정 문제에만 적용이 가능하다.

투 포인터 알고리즘 예제 (two sum)

def two_sum_sorted(arr, target):
    left, right = 0, len(arr) - 1
    while left < right:
        current_sum = arr[left] + arr[right]
        if current_sum == target:
            return (left, right)
        elif current_sum < target:
            left += 1
        else:
            right -= 1
    return None

# 사용 예제
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
target = 10
print(two_sum_sorted(arr, target))  # 출력: (0, 8)