Regression

Data 준비

Data 불러오기

• https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques/data?select=train.csv

import pandas as pd
import numpy as np

# House Price Data의 train data 이용  
data = pd.read_csv(os.path.join(path,file), index_col=None)
data.head()

Data preprocessing

data.shape  # (1640, 81)
data.info()  # Alley, FireplaceQu, PoolQC, Fence, MiscFeature 카럼에서 결측치가 많은 것을 확인
na_feat = ['Alley', 'FireplaceQu, 'PoolQC', 'Fence', 'MiscFeature']  # 결측치가 많은 항목들
data.drop(na_feat, inplace=True, axis=1)  # inplace가 True이면 메소드가 적용된 df로 기존 df 대체
data.shape  # (1640, 76)

# Target Feature 지정
y = data['SalePrice']
data.drop(['Id', 'SalePrice'], axis=1, inplace=True)

for i in data.columns[data.isna(),sum()>0]:
	if data[i].dtype=='object':
    	data[i] = data[i].fillna('None')
    else:
    	data[i] = data[i].fillna(-1)

실행결과

Scaling

# numerical features
numerical_f = list(data.columns[data.dtypes!='object'])
# numerical feature에서 제외할 항목 선택
numerical_f.remove('YrSold')
numerical_f.remove('YearBuilt')
numerical_f.remove('YearRemodAdd')
# numerical feature를 object로 변환
data['YrSold'] = data['YrSold'].astype('object')
data['YearBuilt'] = data['YearBuilt'].astype('object')
data['YearRemodAdd'] = data['YearRemodAdd'].astype('object')

# Scaling
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()

data[numerical_f] = scaler.fit_transform(data[numerical_f])
data.head()

실행결과

Labeling

categorical_f = list(data.columns[data.dtypes=='object'])

from sklearn.preprocessing import LabelEncoder
encoder = LabelEncoder()

for i in categorical_f:
	data[i] = encoder.fit_transform(data[i])

data.head()

실행결과

Train_test_split

from sklearn.model_selection import train_test_split

print(data.shape, y.shape)  # (1460, 74) (1460,)

x_train, x_test, y_train, y_test = train_test_split(data, y, test_size=0.2, random_state=0)

print('train data: ', x_train.shape, y_train.shape)  # train data: (1168, 74) (1168,)
print('test data; ', x_test.shape, y_test.shape)  # test data: (292, 74) (292,)

Regression metric

• 회귀 문제에서 사용되는 평가 지표 및 수식

Mean Absolute Error (MAE)

$\frac{1}{n}\sum^{n}_{i=1}(\left\lvert y_i - \hat{y}_i \right\rvert)$

from sklearn.metrics import mean_squared_error
mean_squared_error(y_t, y_pred)

실행결과

Root Mean Squared Error (RMSE)

$RMSE=\sqrt{\sum^{n}_{i=1}\frac{(y_i-\hat{y}_i)^2}{n}}$

• MSE의 제곱이 에러를 크게 보기 때문에 루트를 씌움
• 에러에 따른 손실이 기하급수적으로 올라갈 때 사용

from sklearn.metrics import mean_squared_error
mean_squared_error(y_t, y_pred)**0.5

실행결과

Root Mean Squared Log Error (RMSLE)

$RMSLE=\sqrt{\frac{1}{n}\sum^{n}_{i=1}(log(\hat{y}_i+1) - log(y_i+1))^2}$

• outlier에 대해 robust함

from sklearn.metric import mean_squared_log_error  
mean_squared_log_error(y_t, y_pred)**0.5  

실행결과

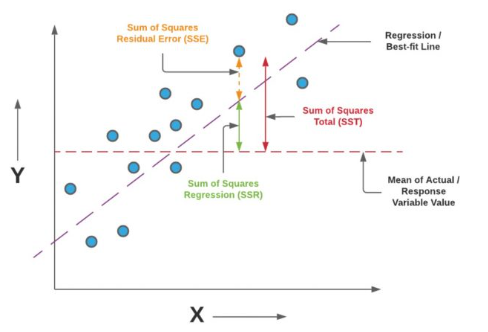
R-squared (결정 계수)

• 독립 변수가 종속 변수를 얼마나 설명하는지
• SSE = Sum of Squared Error
• SST = Sum of Squared Total
• $R^2 = 1 - \frac{SSE}{SST}$
• $SSE = \sum_{i=1}^{m}(\hat{y}_i - y_i)^2$
• $SST = \sum_{i=1}^{m}(y_i - \bar{y}_i)^2$

from sklearn.metrics import r2_score
r2_score(y_t, y_pred)  # 음수인 경우 모델의 예측값이 평균값으로 예측하는 것보다 부정확  

실행결과

Adjusted R-squared

• 독립 변수가 증가할 때 R-squared의 일방적인 증가를 방지하기 위함

$Adjusted R^2 = 1 - \frac{SSE / (n-p-1)}{SST / (n-1)} = 1 - (1 - R^2)\frac{n-1}{n-p-1}$

n : 표본 수, p : 독립변수의 갯수
SST(총 변동) = SSR(설명 가능한 변동) + SSE(설명 불가능한 변동)

R2 = r2_score(y_t, y_pred)
n = len(y_t)  # n값이 커질수록 p의 영향도가 작아짐
p = 5  # p값이 커질수록 값이 작아짐
adj_R2 = 1-((1-R2)*(n-1)/(n-p-1))
adj_R2

실행결과

Linear Regression

$Y_i = \beta_0 + \beta_1X_1 + \beta_2X_2 + ... + \beta_nX_n + \epsilon$

회귀모델 생성

from sklearn.linear_model import LinearRegression
lr = LinearRegression()

lr.fit(x_train, y_train)

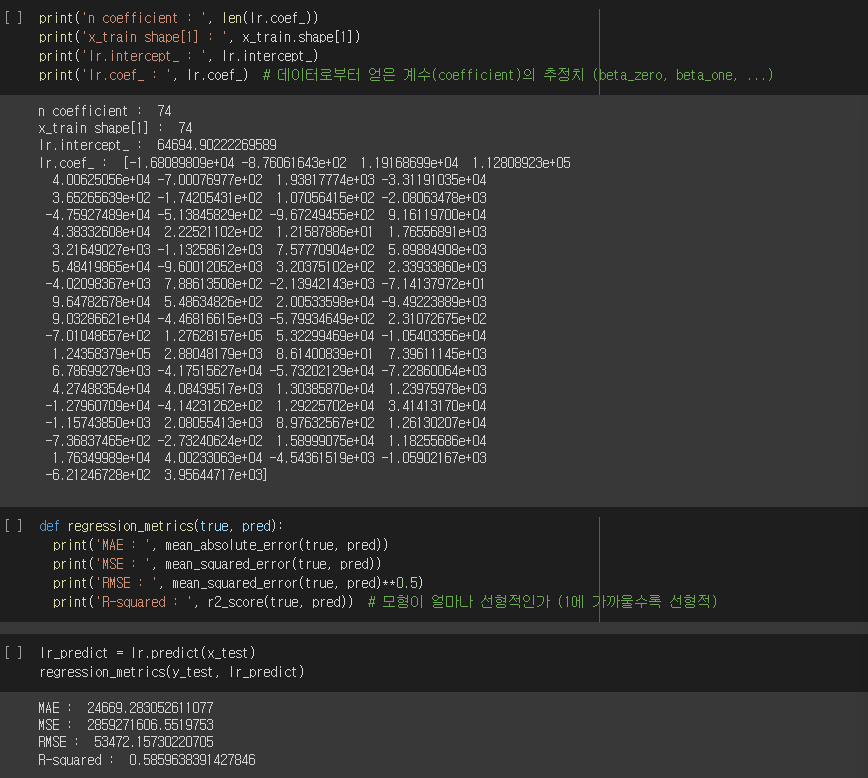
print('n coefficient :', len(lr.coef_))
print('x_train shape[1] :', x_train.shape[1])
print('lr.intercept_ : ', lr.intercept_)
print('lr.coef_ : ', lr.coef_)  # 데이터로부터 얻은 계수(coefficient)의 추정치 (beta0, beta1, ...)

def regression_metrics(true, pred):
	print('MAE : ', mean_absolute_error(true, pred))
    print('MSE : ', mean_squared_error(true, pred))
    print('RMSE : ', mean_squared_rror(true, pred)**0.5)
    print('R-squared : ', r2_score(true, pred))  # 모형이 얼마나 선형적인가 (1에 가까울수록 선형적)
    
lr_predict = lr.predict(x_test)
regression_metrics(y_test, lr_predict)

실행결과

변수 선택 (Subset Selection)

• 회귀모델에서는 변수가 많은 경우 예측 성능이 낮아진다.
• 추정의 신뢰성을 높이기 위해서는 변수를 줄여야 한다.
• Subset Selection을 통해 기준을 가지고 변수를 줄일 수 있다.

AIC (Akaike Information Criterion)

• MSE에 변수의 수 만큼 penalty를 주는 지표
  $AIC = -2\ln(LogLikelihood) + 2p$
  p : 변수 갯수, n : 데이터 갯수
  

BIC (Bayes Information Criterion)

• 표본(n)이 커질 때 부정확해지는 AIC의 단점을 보완하기 위한 지표
• n이 8 이상일 때 $2p < p\ln{n}$
  $BIC = -2\ln(LogLikelihood) + p\ln{n}$
  p : 변수 갯수, n : 데이터 갯수
  

Linear Regression (선형 회귀 분석)

• 전제:
• x는 독립변수이어야 함 (왜냐하면 비슷한 변수가 두 번 학습되는 것을 막기 위해)
• 변수들은 정규분포에 따라야 함
• x(독립변수)와 y(종속변수)는 선형 관계를 가진다고 가정함
• statsmodels는 python에서 다양한 통계 분석을 할 수 있도록 하는 기능을 제공함
• OLS 회귀분석 (Ordinary Least Squares)은 회귀 모델을 구현하는 method

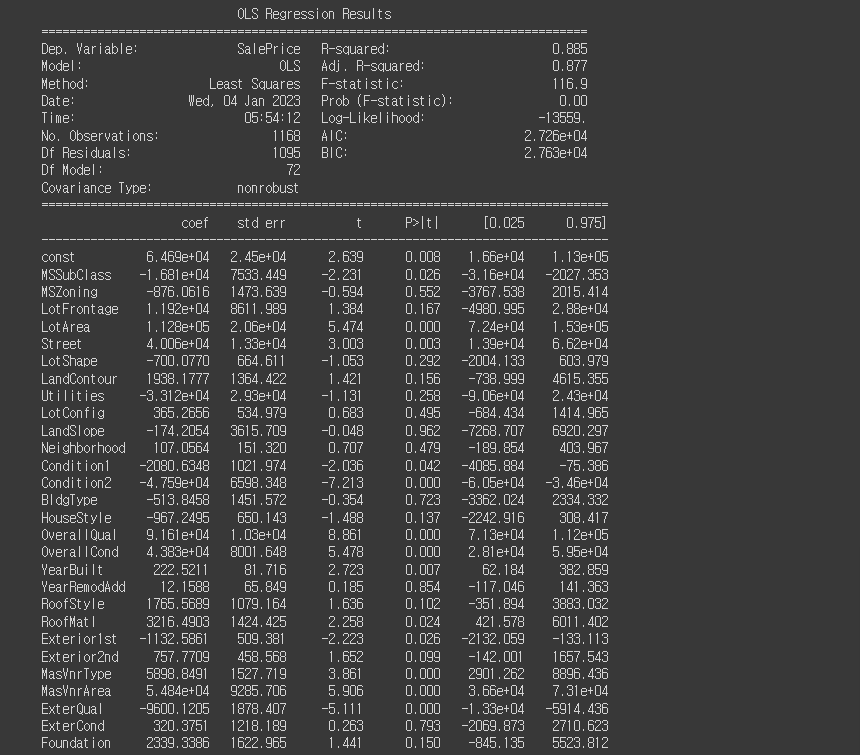
import statsmodels.api as sm

X = sm.add_constant(x_train)
sm_lr = sm.OLS(y_train, X)
sm_lr = sm_lr.fit()
print(sm_lr.summary())

실행결과

X_t = sm.add_constant(x_test)
sm_lr_predict = sm_lr.predict(X_t)
regression_metrics(y_test, sm_lr_predict)  

실행결과

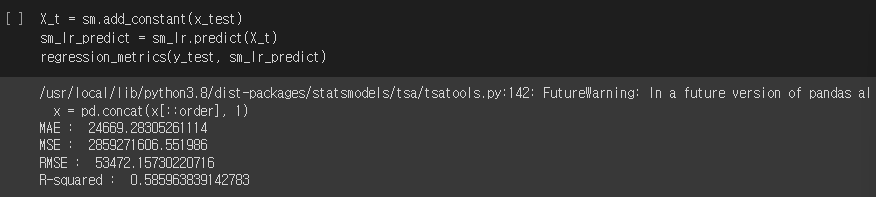
Regularization

• 모델에서 계수의 크기를 줄이기 위해 regularization을 이용
• Lasso Regression (L1 Regularization)
• Ridge Regression (L2 Regularization)
• Elastic-Net (Lasso와 Ridge의 하이브리드 모델)

Lasso

from sklearn.linear_model import Lasso, Ridge, ElasticNet

alphas = [10, 1, 0.1, 0.01]

for alpha in alphas:
	lasso = Lasso(alpha=alpha, random_state=0)
    lasso.fit(x_train, y_train)
    pred = lasso.predict(x_test)
    print(f'alpha = {alpha}')
    regression_metrics(y_test, pred)
    print("\n")

실행결과

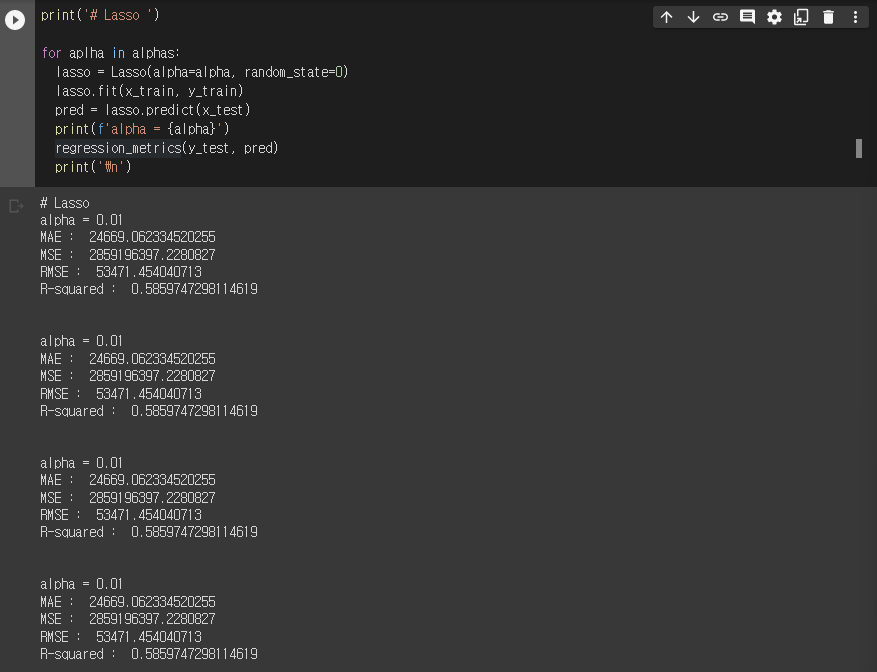
Ridge

alphas = [10, 1, 0.1, 0.01]

for alpha in alphas:
	ridge = Ridge(alpha=alpha, random_state=0)
    ridge.fit(x_train, y_train)
    pred = ridge.predict(x_test)
    print(f'alpha = {alpha}')
    regression_metrics(y_test, pred)
    print("\n")

실행결과

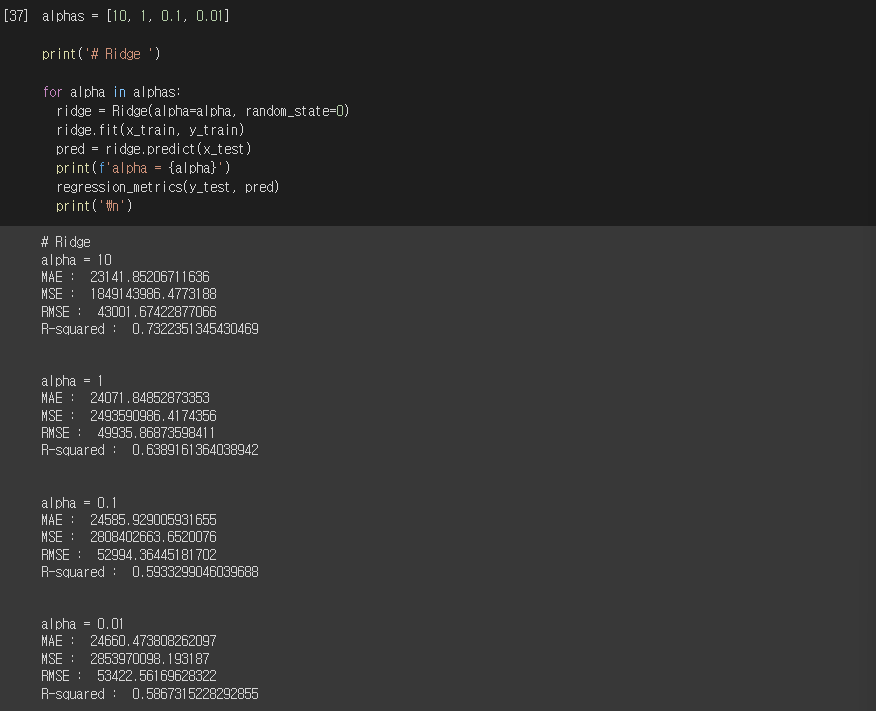
Elastic-Net

ratios = [0.2, 0.5, 0.8]

for ratio in ratios:
	en = ElasticNet(alpha=1, 11_ratio=ratio, random_state=0) # alpha default = 1.0
    en.fit(x_train, y_train)
    pred = en.predict(x_test)
    print(f'ratio = {ratio}')
    regression_metrics(y_test, pred)
    print("\n")

실행결과

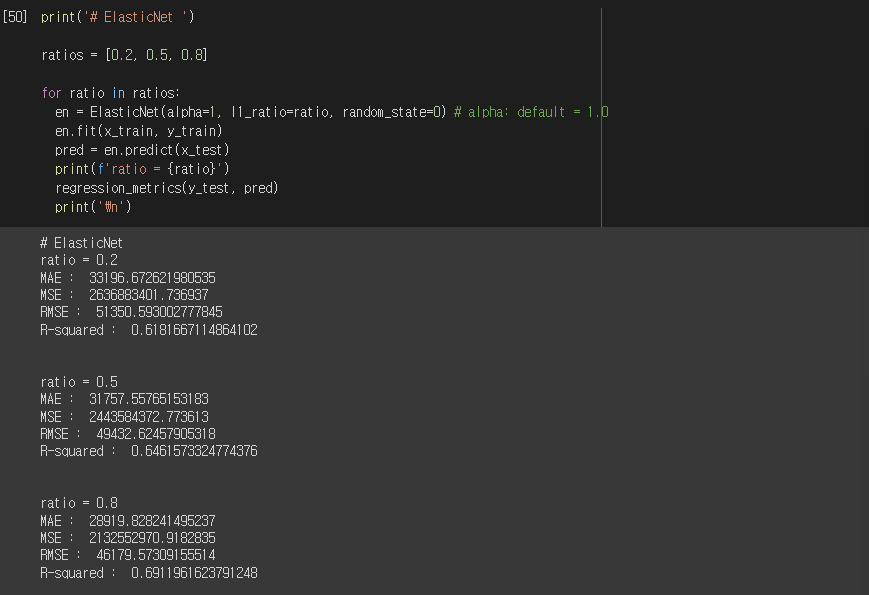
Logistic Regression

• 로지스틱 회귀분석은 이진 분류를 수행하는데 주로 사용됨
• 각 속성의 계수 log-odds를 구한 후 sigmoid 함수를 적용하여 데이터가 특정 클래스에 속할 확률을 0과 1 사이의 값으로 나타냄
• $odds = \frac{p(y=1|x)}{1-p(y=1|x)}$, 성공 확률이 실패 확률에 비해 몇 배 더 높은지.
• $logit(p) = \log{\frac{p}{1-p}}$, range : [0,1]

from sklearn.linear_model import LogisticRegression

logistic = LogisticRegression()
logistic.fit(x_train, y_train)
logistic_pred = logistic.predict_proba(x_test)  # predict_proba 함수는 각 샘플에 대해 어느 클래스에 속할지 확률을 0과 1 사이의 값으로 리턴

np.min(logistic_pred)
np.max(logistic_pred)

실행결과

Bagging vs Boosting

Bagging

• 샘플을 여러번 뽑아 각 모델을 학습시켜 결과를 집계 (Bootstrap Aggregating)
• 각 샘플에서 나타난 결과를 일종의 중간값으로 맞춰주기 때문에 overfitting을 피할 수 있음
  • categorical data의 경우 voting으로 집계
  • continuous data의 경우 평균으로 집계
• Random Forest 모델

Boosting

• 맞히기 어려운 문제를 맞히는데 초점
• Bagging과 동일하게 복원 랜덤 샘플링을 하지만 가중치를 부여
• Bagging은 병렬로 학습 / Boosting은 순차적으로 학습
• outlier에 취약
• AdaBoost, XGBoost, GradientBoost 모델

from sklearn.ensemble import AdaBoostRegressor

adaboost = AdaBoostRegressor()
adaboost.fit(x_train, y_train)
adaboost_pred = adaboost.predict(x_test)
regression_metrics(y_test, adaboost_pred)

실행결과

from sklearn.ensemble import GradientBoostingRegressor

GBM = GradientBoostingRegressor()
GBM.fit(x_train, y_train)
GBM_pred = GBM.predict(x_test)
regression_metrics(y_test, GBM_pred)

실행결과

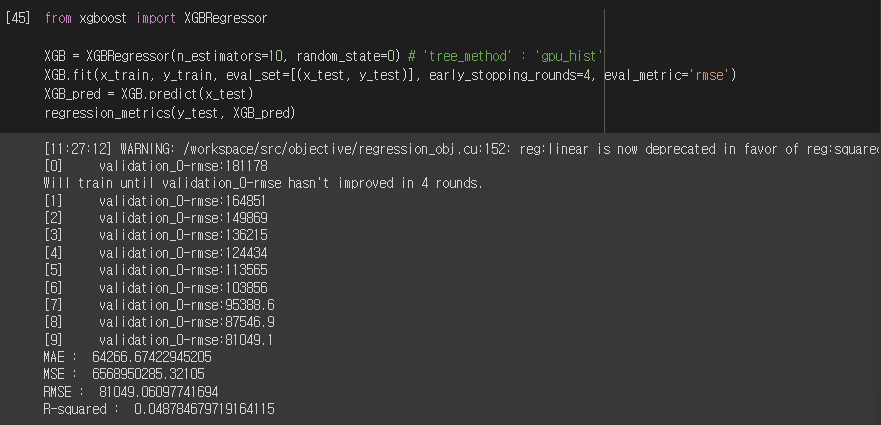
from xgboost import XGBRegressor

XGB = XGBRegressor(n_estimators=10, random_state=0)  # 'tree_method' : 'gpu_hist'
XGB.fit (x_train, y_train, eval_set=[(x_test,y_test)], early_stopping_rounds=4, eval_metric='rmse')
XGB_pred = XGB.predict(x_test)
regression_metrics(y_test, XGB_pred)

실행결과

Light GBM

• 기존 tree 기반 알고리즘의 level wise 방식 대신 leaf-wise 방식을 사용
• tree의 depth에 민감
• GOSS(Gradient-based One-Side Sampling) 작은 gradient를 가진 data를 랜덤하게 drop
• 장점:
  - XGBoost에 비해 빠른 학습, 추론
  • XGBoost에 비해 적은 메모리 사용
  • categorical feature의 자동 변환
• 단점:
  - 작은 데이터셋에서 overfit 위헙

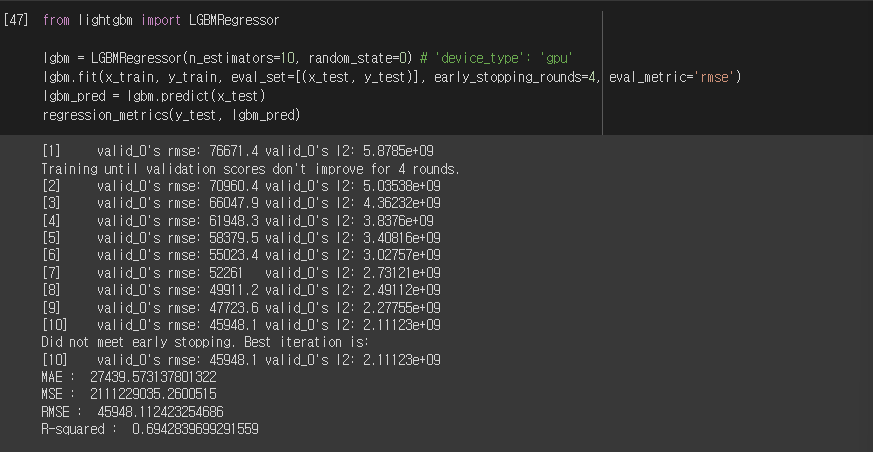
from lightgbm import LGBMRegressor

lgbm = LGBMRegressor(n_estimators=10, random_state=0)  # 'device_type' : 'gpu'
lgbm.fit(x_train, y_train, eval_set=[(x_test, y_test)], early_stopping_rounds=4, eval_metric='rmse')
lgbm_pred = lgbm.predict(x_test)
regression_metrics(y_test, lgbm_pred)

실행결과

CatBoost

• TS(Target Statistics): categorical feature를 numerical data로 변환하는 새로운 방법
• Ordered Boosting: 기존 부스팅 모델이 일괄적으로 모든 train data에 대해 residual을 계산했다면, catboost는 일부 데이터만 가지고 residual을 계산하는 모델을 만들고 그 뒤 데이터의 residual은 이 모델로 예측한 값을 사용

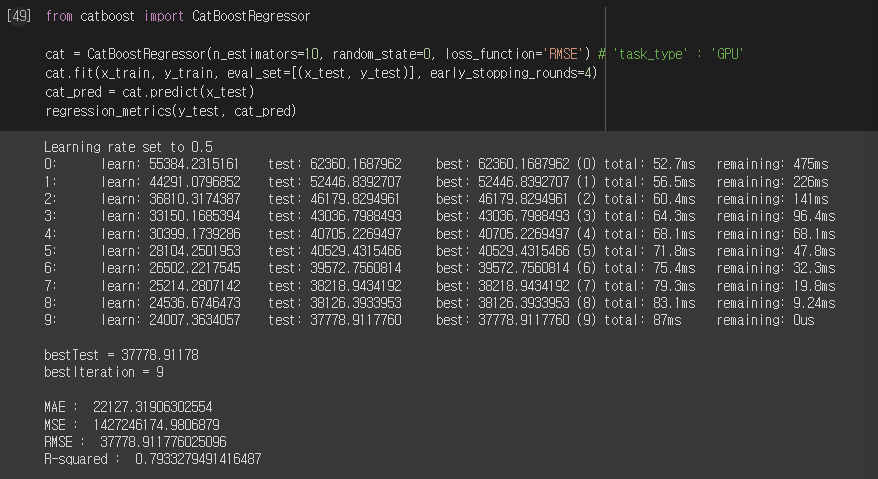
from catboost import CatBoostRegressor

cat = CatBoostRegressor(n_estimators=10, random_state=0, loss_function='RMSE')  # 'task_type' : 'GPU'
cat.fit(x_train, y_train, eval_set=[(x_test, y_test)], early_stopping_rounds=4)
cat_pred = cat.predict(x_test)
regression_metrics(y_test, cat_pred)

실행결과