1. 정의

• 한 개의 모집단을 이루고 있는 양적 자료의 모평균에 대한 가설검정
• 모평균의 변화가 있는지 통계적으로 검정

2. One sample test road map

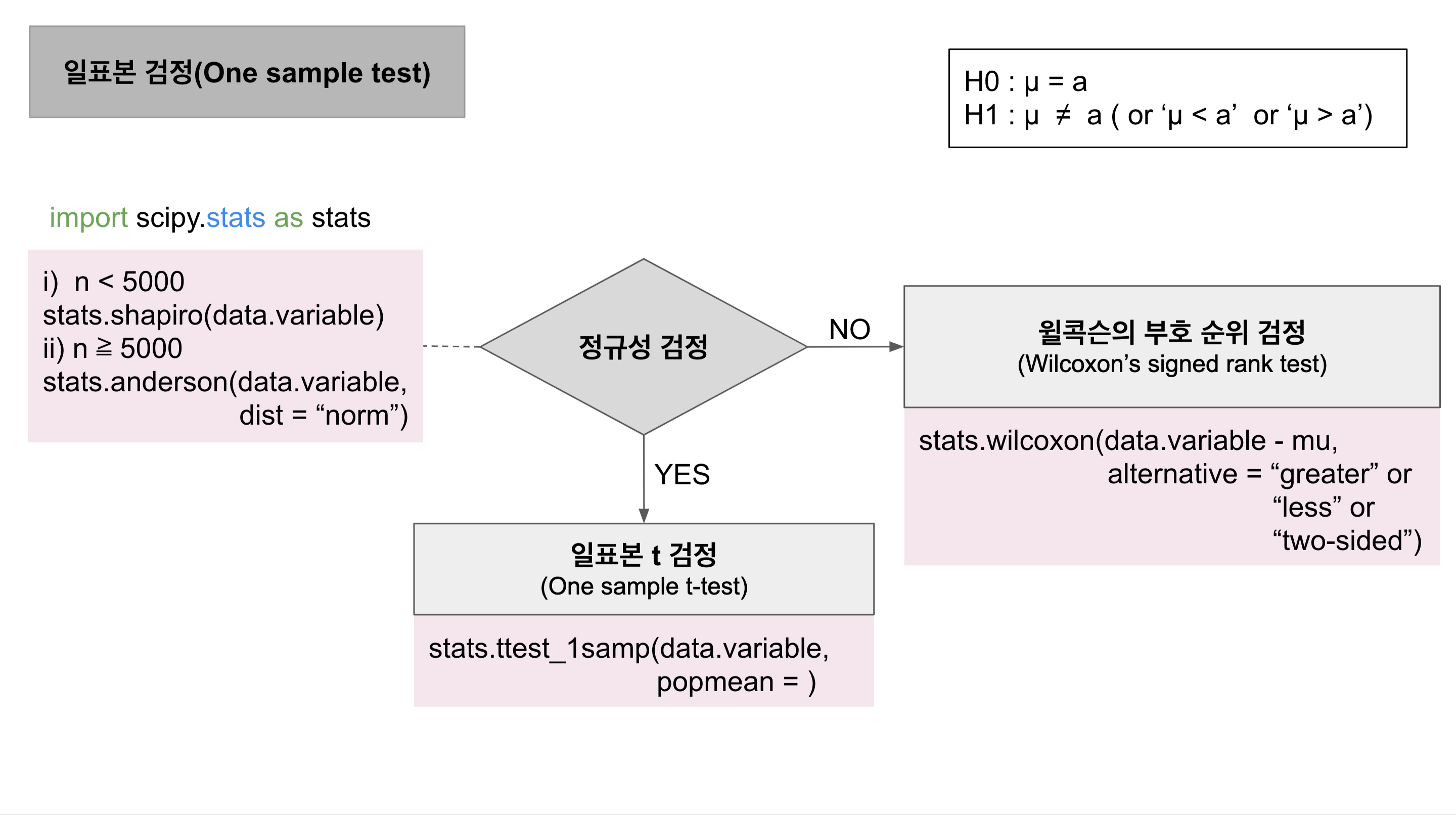
3. 정규성 검정 (Normality test)

• 정규성 검정 결과에 따라 정규분포를 가정할 수 있으면 일표본 t검정, 가정할 수 없다면 윌콕슨의 부호 순위 검정을 실시

1) 방법

(1) 가설

• 귀무가설 : 표본의 모집단이 정규분포를 따른다.
• 대립가설 : 표본의 모집단이 정규분포를 따르지 않는다.

(2) Shapiro-Wilk Normality test

• 데이터의 개수가 5000개 미만일 때 보편적으로 사용

  import scipy.stats as stats
   stats.shapiro(data.variable)

(3) Anderson-Darling Normality test

• 데이터의 개수가 5000개 이상일 때 보편적으로 사용

  stats.anderson(data.variable, dist = 'norm')
   # dist : distribution
   # 'norm' : normal distributution

  
• 결론 : 유의수준 0.05에서 검정통계량 3474.016이고 임계값이 0.787보다 크므로 price는 정규분포를 따르지 않는다. 즉, 대립가설을 지지한다.

4. One sample t-test

• 정규 분포의 평균을 측정할 때 많이 사용하는 분포
• 모집단이 정규분포라는 것을 알고 모분산을 모를 때, 표본분산으로 대체하여 모 평균 mu를 구할 때 사용

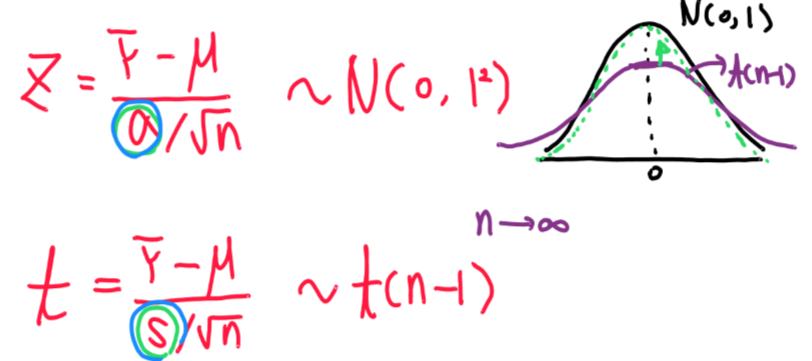
1) 방법

(1) 가설

• 귀무가설 : ~의 평균은 ~이다.
• 대립가설 : ~의 평균은 ~보다 많다, 적다, 가 아니다.

(2) Code

stats.ttest_1samp(data.variable, popmean = )
# popmean : 귀무가설을 모평균(mu)

• 결론 : 유의확률이 0.000이므로 유의수준 0.05에서 다이아몬드 무게에 통계적으로 유의하게 작아진 것으로 나타났다.

  주의사항!
  파이썬에서는 유의확률 값을 양쪽의 값을 모두 주기 때문에 /2가 필수적으로 적용되어야 한다.

5. Wilcoxon's signed rank test

• 모집단의 양적 자료가 정규분포를 따르지 않을 때 사용
• 정규성 가정이 깨질 때 사용

1) 방법

(1) 가설

• 귀무가설 : ~의 평균은 ~이다.
• 대립가설 : ~의 평균은 ~보다 많다, 적다, 가 아니다.

(2) Code

stats.wilcoxon(data.variable - mu, alternative = 'greater' or 'less' or 'two.sided')
# data.variable - mu : wilcoxon mu의 기본값은 0
# alternative : 대립가설
# 'greater'   = mu > 0
# 'less'      = mu < 0
# 'two-sided' = mu != 0

• 결론 : 유의확률이 0.5이므로 유의수준 0.05에서 다이아몬드 가격은 통계적으로 유의하게 변하지 않았다.

One sampe t-test는 Wilcoxon test보다 검정력이 더 높기 때문에 t-test가 더 선호된다.
Wilcoxon test는 정보손상 또는 순위변동을 일으킬 수도 있다.
다만, 정규성 가정이 깨지면 Wilcoxon test를 수행한다.