정리 배경 (ft. 🧐의식의 흐름)
다익스트라 문제를 javascript로 풀려고 함 ➡️ 최소힙을 어떻게 구현하지? ➡️ 완전 이진트리로 힙 구현 ➡️ 이진트리 ? 완전 이진트리? 정 이진트리? 트리의 개념을 확실히 알고 있나?
아니다➡️ 이참에 정리해보자
🎄Complete Binary Tree? (완전 이진 트리)
🎄 이진트리 종류 중 하나.
🎄 마지막 노드 제외 모든 노드들이 꽉찬 경우
🎄 마지막 노드들이 있는 레벨은 가장 왼쪽에서부터 채움
🎄 쓰임 : heap sort
📑완전 이진트리 용어 정리
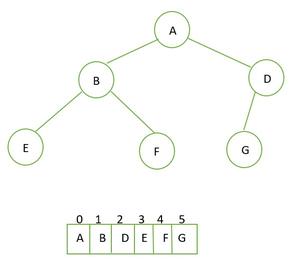
- Root : 부모노드로부터 edge가 연결되지 않는 노드 (부모가 없는 최상위 노드)
- Child : 부모노드로부터 뻗어나오는 edge가 있는 노드
- Sibling : 같은 부모가 있는 노드들 (형제/자매 노드)
- Degree of a node : 한 부모 노드로부터 나온 자식 노드의 개수
- Leaf : 자식 노드가 없는 노드
- Internal/External nodes : leaf nodes == Internal nodes, leaf nodes != External nodes
- Level : 목적지 노드로부터의 노드 개수. ex) Level of node D is 2 as nodes A and E for the path
- Height : 목적 노드로부터의 edge 개수. Root는 height가 0. ex) node E의 height는 2이다 (root로부터 edge가 2개이므로)
완전 이진트리의 특성들
🫠 모든 leaf들이 같은 depth가 있는 적절한 이진트리라고 한다.
😝 depth가 d일때 노드의 개수 = 2^d
😛 노드의 개수가 n개인 트리의 높이는 log(n+1)
😊 마지막 level을 제외한 모든 level들은 완전히 차 있다.
📝 Complete Binary Tree(완전 이진트리) vs Perfect Binary Tree (포화 이진 트리)
🌳높이가 h인 이진트리에서 최대 노드개수를 꽉채운(포화) 트리를 포화 이진트리 (
perfect binary tree)라고 부름.
🌲 트리의 높이가 h라고 하면 최대 노드의 개수는2^(h+1)-1개
🎄 완전 이진트리는 높이가 총h일 때, h-1높이까지는proper binary tree고, 마지막 level은 왼쪽에서부터 순서대로 element가 채워져 있는 형태.
🙋♀️ 트리 구분하기 (퀴즈)
퀴즈 1: 완전 이진트리 T/F , 포화 이진트리 T/F ?
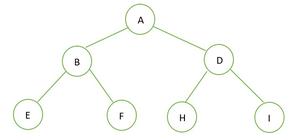
정답 : 포화 이진트리 🙆♂️(T), 완전 이진트리🙆♂️(T)
해설
🎄포화 이진트리인 이유 : 높이가 2인 트리인데 최대 노드의 개수가 2^(h+1)-1 = 2^(2+1)-1=7이므로 완전 이진트리라고 할 수 있다.
🎄완전 이진트리인 이유 : h-1 즉 첫번째 level에서 양쪽 노드들로 차 있고, 마지막 level에서는 왼쪽에서 오른쪽으로 element들이 저장되어 있음.
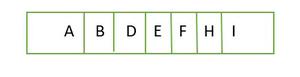
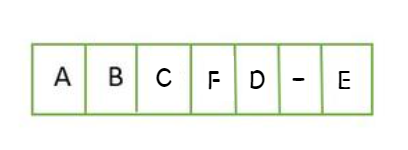
👉 배열 형태로 보기
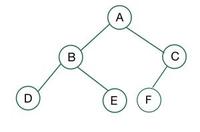
퀴즈 2: 완전 이진트리 T/F , 포화 이진트리 T/F ?
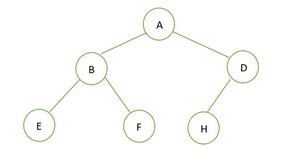
정답 : 포화 이진트리 🙅♀️(F), 완전 이진트리🙆♂️(T)
해설
🎄포화 이진트리가 아닌 이유 : 높이가 2인 트리인데 최대 노드의 개수가 2^(h+1)-1 = 2^(2+1)-1=7인데 현재 트리의 노드개수는 6이다. 따라서 포화 이진트리가 아님!
🎄완전 이진트리인 이유 : h-1 즉 첫번째 level에서 양쪽 노드들로 차 있고, 마지막 level에서는 왼쪽에서 오른쪽으로 element들이 저장되어 있음.
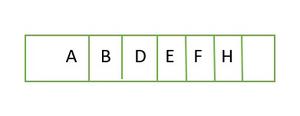
👉 배열 형태로 보기
퀴즈 3: 완전 이진트리 T/F , 포화 이진트리 T/F ?
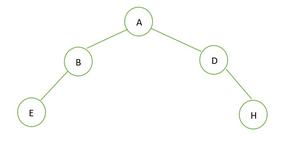
정답 : 포화 이진트리 🙅♀️(F), 완전 이진트리🙅♀️(F)
해설
🎄포화 이진트리가 아닌 이유 : 높이가 2인 트리인데 최대 노드의 개수가 2^(h+1)-1 = 2^(2+1)-1=7인데 현재 트리의 노드개수는 5이다. 따라서 포화 이진트리가 아님!
🎄완전 이진트리가 아닌 이유 : h-1 즉 첫번째 level에서 양쪽 노드들이 차 있지도 않고, 마지막 level에서는 왼쪽 부터 element들이 저장되어 있지않음.
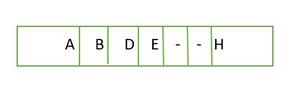
👉 배열 형태로 보기
📝 Full Binary Tree(정 이진 트리) vs Complete Binary tree(완전 이진트리)
full binary tree : 모든 노드들의 자식노드의 개수가 2이거나 0이다.
퀴즈 1: 완전 이진트리 T/F , 정 이진트리 T/F ?
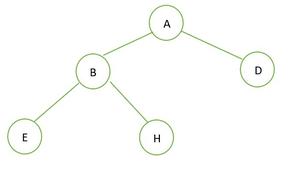
정답 : 정 이진트리 🙆♂️(T), 완전 이진트리🙅♀️(F)
해설
🎄정 이진트리인 이유 : 루트 노드를 제외한 모든 노드들이 자식노드가 없거나 있으면 2개다.
🎄완전 이진트리가 아닌 이유 : 트리의 각 level이 왼쪽부터 채워져야하는데 현재 그래프는 왼쪽이 비워져 있다.
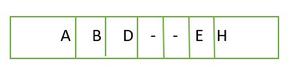
👉 배열 형태로 보기
퀴즈 2: 완전 이진트리 T/F , 정 이진트리 T/F ?
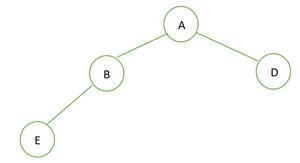
정답 : 정 이진트리 🙆♂️(T), 완전 이진트리🙆♂️(T)
해설
🎄정 이진트리인 이유 : 루트 노드를 제외한 모든 노드들이 자식노드가 없거나 있으면 2개다.
🎄완전 이진트리인 이유 : 트리의 각 level이 왼쪽부터 채워져 있다.
👉 배열 형태로 보기
퀴즈 3: 완전 이진트리 T/F , 정 이진트리 T/F ?
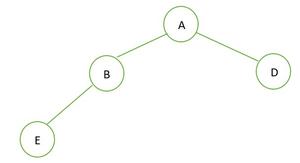
정답 : 정 이진트리 🙅♀️(F), 완전 이진트리🙆♂️(T)
해설
🎄정 이진트리가 아닌 이유 : 노드 B의 자식이 하나뿐이다.
🎄완전 이진트리인 이유 : 트리의 각 level이 왼쪽부터 채워져 있다.
👉 배열 형태로 보기
퀴즈 4: 완전 이진트리 T/F , 정 이진트리 T/F ?
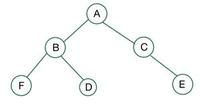
정답 : 정 이진트리 🙅♀️(F), 완전 이진트리🙅♀️(F)
해설
🎄정 이진트리가 아닌 이유 : 노드 C의 자식이 하나뿐이다.
🎄완전 이진트리가 아닌 이유 : 트리의 각 level이 왼쪽부터 채워져 있지 않다. E가 왼쪽으로 가 있었다면 이 조건에 맞게 완전 이진트리가 되었을 것이다.
👉 배열 형태로 보기
🛠️ 완전 이진트리 만들기
지금까지 완전 이진트리를 살펴보면서 완전 이진트리는
- l까지의 level이 있을 때 l-1까지 node들이 2l이고 왼쪽부터 채워져 있음
- 배열을 통해 표현 가능
- 부모 인덱스가 i라면, 왼쪽 자식은 2i+1이고 오른쪽 자식은 2i+2이다.
🤖 알고리즘
queue를 활용해서 node 삽입 삭제 추적
-
빈 tree의 시작인 root를 새로운 노드로 초기화

-
빈 트리가 아니라면 맨 앞 element를 가져오기
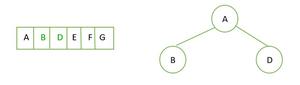
- 맨 앞 element가 왼쪽 자식이 없다면 새 노드를 왼쪽 자식으로 삼기
- 맨 앞 element가 오른쪽 자식이 없다면 새 노드를 오른쪽 자식으로 삼기
-
노드가 왼쪽과 오른쪽 자식 둘다 있다면 queue에서 둘다
pop하기
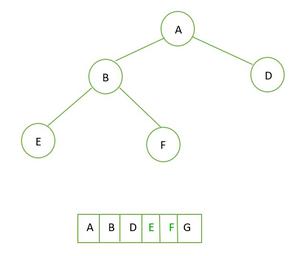
-
새 데이터 queue로 줄 세우기
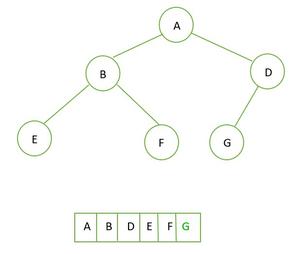
🌲 javascript로 완전이진 트리 만들기
let root;
class Node
{
constructor(data) {
this.left = null;
this.right = null;
this.data = data;
}
}
// Function to insert nodes in level order
function insertLevelOrder(arr, i)
{
let root = null;
// Base case for recursion
if (i < arr.length) {
root = new Node(arr[i]);
// insert left child
root.left = insertLevelOrder(arr, 2 * i + 1);
// insert right child
root.right = insertLevelOrder(arr, 2 * i + 2);
}
return root;
}
// Function to print tree nodes in InOrder fashion
function inOrder(root)
{
if (root != null) {
inOrder(root.left);
document.write(root.data + " ");
inOrder(root.right);
}
}
let arr = [ 1, 2, 3, 4, 5, 6, 6, 6, 6 ];
root = insertLevelOrder(arr, 0);
inOrder(root);
/*
output:
1
/ \
2 3
/ \ / \
4 5 6 6
/ \ /
6 6 6
*/
마무리
📝
이 포스트에서는 힙을 구현하기 위한 자료구조로 완전 이진트리에 집중해서 정리했다.
🎄 공부를 하면서 자료들을 찾아보니 트리의 종류에는 여러가지가 있다. red black tree, avl tree , 이진탐색 tree 등등..
🤔 그리고 오늘 살펴본 level order (bfs)방식 말고도 트리들을 순회하는 방식들 (preorder traversal, postorder)이 여러 있다.
🤖 다음 포스팅에는 트리의 종류와 트리 순회에 대해 정리하자.의식의 흐름 멈춰😂😂😂😂