🤔python으로 코딩 테스트 문제풀이를 하면 heapq를 활용해서 쉽게 heap 자료구조를 사용할 수 있다.
👀하지만 js에는 내장된 힙 자료구조가 없다.
💡다익스트라 문제 풀이를 하던 도중, 최소 힙을 활용하고 싶어서 js로 힙 class 구현을 정리해보았다.

📄전체 코드

• 두괄식을 선호해서 코드먼저 보고 가기

class MinHeap {
    constructor() {
        this.heap = [ null ];
    }
    
    size() {
        return this.heap.length - 1;
    }
    
    getMin() {
        return this.heap[1] ? this.heap[1] : null;
    }
    
    swap(a, b) {
        [ this.heap[a], this.heap[b] ] = [ this.heap[b], this.heap[a] ];
    }
    
    heappush(value) {
        this.heap.push(value);
        let curIdx = this.heap.length - 1;
        let parIdx = (curIdx / 2) >> 0;
        
        while(curIdx > 1 && this.heap[parIdx] > this.heap[curIdx]) {
            this.swap(parIdx, curIdx)
            curIdx = parIdx;
            parIdx = (curIdx / 2) >> 0;
        }
    }
    
    heappop() {
        const min = this.heap[1];	
        if(this.heap.length <= 2) this.heap = [ null ];
        else this.heap[1] = this.heap.pop();   
        
        let curIdx = 1;
        let leftIdx = curIdx * 2;
        let rightIdx = curIdx * 2 + 1; 
        
        if(!this.heap[leftIdx]) return min;
        if(!this.heap[rightIdx]) {
            if(this.heap[leftIdx] < this.heap[curIdx]) {
                this.swap(leftIdx, curIdx);
            }
            return min;
        }

        while(this.heap[leftIdx] < this.heap[curIdx] || this.heap[rightIdx] < this.heap[curIdx]) {
            const minIdx = this.heap[leftIdx] > this.heap[rightIdx] ? rightIdx : leftIdx;
            this.swap(minIdx, curIdx);
            curIdx = minIdx;
            leftIdx = curIdx * 2;
            rightIdx = curIdx * 2 + 1;
        }

        return min;
    }
}

🤔힙(Heap)?

• why heap? 우선순위 큐 구현할 때 사용할 자료구조.
• 이진트리 구조라 삽입과 삭제에 O(logN)의 시간 소요.
• 최대힙과 최소힙이 있다.
• 최대힙은 부모 노드의 값이 자식 노드의 값보다 큰 힙.
• 최소힙은 반대로 부모노드의 값이 자식 노드의 값보다 작은 힙.
• 힙은 느슨한 완전이진트리이기 때문에 배열로 쉽게 구현 가능.
• 느슨하다 == 최대힙이라면 큰 값이 부모 노드쪽에, 최소힙이라면 작은값이 부모 노드 쪽에 배치되는 것만 유지
• 왼쪽 자식과 오른쪽 자식은 부모노드보다 작은 값만 유지하면 됨

🎄완전 이진트리

• 이진트리 (Binary Tree) : 노드의 유한집합. 공집합이거나 루트와 왼쪽, 오른쪽 서브트리로 두개의 분리된 이진트리로 구성 😣쉽게 말해서 하나의 부모 노드로 부터 2개의 자식 노드가 각각 왼쪽과 오른쪽에 있는 트리 형태!
  

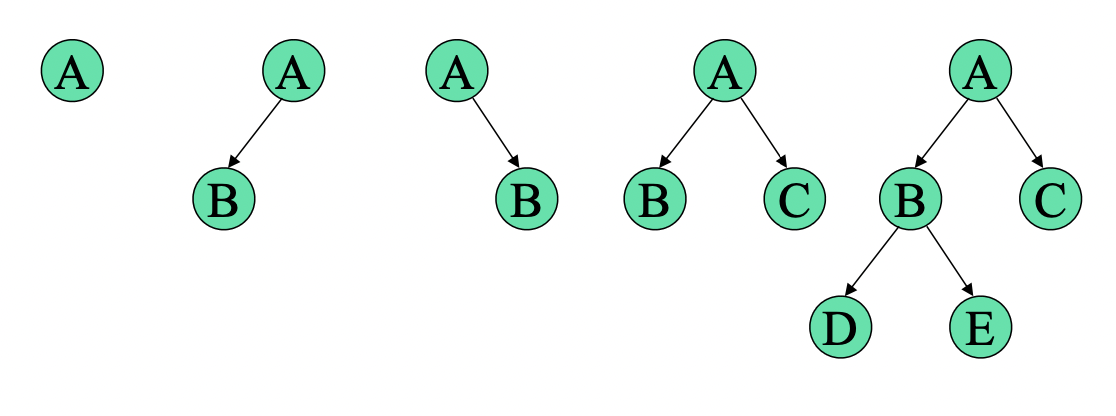
포화 (Full) 이진트리 ? 완전(Complete) 이진트리 ?

• 포화 (Full) 이진트리 : 이진트리이면서 서브트리까지 모두 빈곳이 없이 꽉찬 트리.

• 완전(Complete) 이진트리 : 높이가 h 일 때 레벨 h-1까지는 포화 이진트리고, 레벨 h에서는 왼쪽부터 노드가 순서대로 채워진 이진트리
  

  • 아래의 그림들 중 뭐가 어떤 건지 잘 구분이 안되거나 배열로 어떻게 들어가는 지 모르면? 👉tree 자료구조 더 알아보기
    

코드 설명

1. 클래스 선언

class MinHeap {
    constructor() {
        this.heap = [ null ];
    }
}

• 인덱스 접근을 하면 +1로 하기 번거러우니까 첫번째 == 인덱스 1로 매칭 되게 0번 배열은 null로 채우기

2. [Helper 함수] heap.size() : heap의 크기 가져오기

size() {
        return this.heap.length - 1;
}

3. [Helper 함수] heap.getMin() : heap의 최소값 가져오기

getMin() {
        return this.heap[1] ? this.heap[1] : null;
}

• 최소힙에서는 부모노드가 제일 작으므로 heap[1]을 리턴해주기. 빈 힙이라면 null을 리턴하기.

4. [Helper 함수] heap.swap() : heap 정렬해주기

swap(a, b) {
        [ this.heap[a], this.heap[b] ] = [ this.heap[b], this.heap[a] ];
}

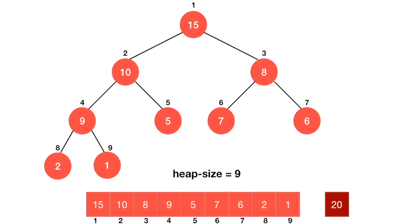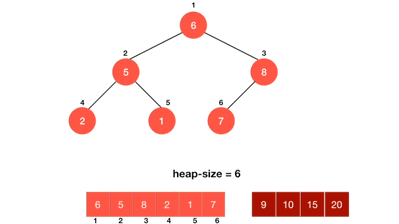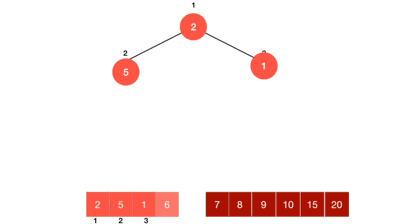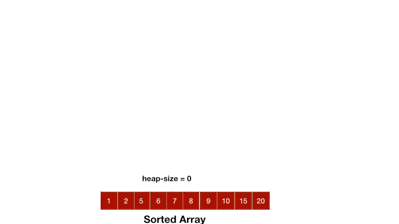
5. heap.heappush() : heap에 삽입하기

    heappush(value) {
        this.heap.push(value);
        let curIdx = this.heap.length - 1;
        let parIdx = (curIdx / 2) >> 0;
        
        while(curIdx > 1 && this.heap[parIdx] > this.heap[curIdx]) {
            this.swap(parIdx, curIdx)
            curIdx = parIdx;
            parIdx = (curIdx / 2) >> 0;
        }
    }

실행 순서

• 1. 마지막 노드에 들어온 값을 push
• 2. 노드들 순회하면서 부모노드와 비교 시 대소 구분해서 위치 교환
• 현재는 최소힙! 부등호를 반대로하면 최대힙

6. heap.heappop() : heap 요소 제거하기

   heappop() {
     // 배열 첫 원소는 비워두기, root 는 항상 heap[1]에 위치
        const min = this.heap[1];	

        if(this.heap.length <= 2) this.heap = [ null ];
   	// 배열 마지막 원소를 root에 먼저 두기 
     else this.heap[1] = this.heap.pop();   
        
        let curIdx = 1; //현재 노드
        let leftIdx = curIdx * 2; //왼쪽 노드
        let rightIdx = curIdx * 2 + 1; //오른쪽 노드
        
     //루트만 있는 상태 == 루트 pop
        if(!this.heap[leftIdx]) return min;
     // 오른쪽에 자식 노드가 없다면 즉, 왼쪽 노드에만 자식이 하나라면
        if(!this.heap[rightIdx]) {
     // 완전 이진트리이기 때문에 왼쪽부터 채워져 있어야함!
     // 왼쪽과 비교해서 교체해주기
            if(this.heap[leftIdx] < this.heap[curIdx]) {
                this.swap(leftIdx, curIdx);
            }
            return min;
        }
	// 자식 노드가 오른쪽, 왼쪽 모두 있는 경우
    // 현재 노드가 왼쪽 또는 오른쪽 큰 지 작은 지를 검사하며 반복
        while(this.heap[leftIdx] < this.heap[curIdx] || this.heap[rightIdx] < this.heap[curIdx]) {
          // 왼쪽과 오른쪽 자식 중에 더 작은 값과 현재 노드 교체
            const minIdx = this.heap[leftIdx] > this.heap[rightIdx] ? rightIdx : leftIdx;
            this.swap(minIdx, curIdx);
            curIdx = minIdx;
            leftIdx = curIdx * 2;
            rightIdx = curIdx * 2 + 1;
        }

        return min;
    }

실행과정

• 1. 루트 노드 항상 먼저 꺼내기
• 2. 빈자리에 가장 마지막 노드 (배열 맨 뒤의 값 가져오기)
• 3. 루트노드에서 부터 재정렬 실행

📑References

• 자료구조 js로 구현
• 포화이진트리 완전이진트리
• 이진트리
• Complete binary tree