백준 문제 풀이 class4문제들을 풀이하기 시작하면서 단순히 구현만하는게 아니라 알고리즘들에 대한 개념을 갖고 적용해서 문제풀이를 진행해야하는 필요성을 느꼈다. 숨바꼭질 3 풀이 中

풀이 방법

• 위와 같이 간선들

정형화된 유형같은데, 익숙해져보자!

😂 많이 풀면 유형 익숙해지겠지! 다익스트라 문제들이 이렇게나 많은데 저거 다 풀면 다익스트라는 껌

1. 시작 노드에서 다른 노드로 갈 때 처음에는 모든 값들을 최대 값인 infinity로 설정.
2. dp 테이블을 만들어서 모든 노드들을 방문하지 않음으로 표시,시작점의 최소거리는 0.
3. 임시로 시작점과 노드들간 바로 연결된 거리는 최소거리 로 업데이트.

• 예를 들면 시작점에서A노드에서 B노드로 이동한다고 했을 때,
  • 시작점 ➡️ A : 2
  • A ➡️ B : 6
• 만약 B로 가는 이동거리가 가장 작다면 B노드는 8로 표시하기 (아니라면 값 유지)

4. 현재 노드와 방문하지 않은 이웃노드들 모두 고려한 후, 현재 노드를 방문처리하기 (방문여부를 따져야 똑같은 경로를 재방문하지 않음)
5. 모든 노드들을 방문했거나 , 노드들 간의 임시 최단거리가 inifinity (시작노드와 남은 노드간의 연결이 없다면)라면 stop!
   6 . 아니라면 방문하지 않은 노드 중 가장 작은 임시 값을 가진 노드를 선택해서 3의 과정을 반복

Problems

해당 문제들은 크래프톤정글 동료들과 알고리즘 스터디를 하면서 푼 문제들과 개인적으로 공부를 위해 푼 문제들을 한 곳에 모아, 다익스트라 문제 유형에 익숙해지고 한눈에 보기 위한 문제 모음들입니다.

🤸‍♀️[2023.06.14] 13549 : 숨바꼭질 3

• 난이도 : 골드IV
  

문제

수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 100,000)에 있고, 동생은 점 K(0 ≤ K ≤ 100,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 0초 후에 2*X의 위치로 이동하게 된다.
수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오.

입력

첫 번째 줄에 수빈이가 있는 위치 N과 동생이 있는 위치 K가 주어진다. N과 K는 정수이다.

출력

수빈이가 동생을 찾는 가장 빠른 시간을 출력한다.

예제

#input
5 17
#output
2

풀이

# 다익스트라 문제
# 준비물 : node담을 list, 방문여부 저장할 dp테이블, 최소비용으로 정렬해줄 heap

import sys
from heapq import heappush, heappop

input = sys.stdin.readline
inf = sys.maxsize

n, k = map(int, input().split())
dp = [inf] * (100001)
heap = []


def dijkstra(n, k):
    if k <= n: #동생의 위치가 수빈의 위치보다 뒤라면 수빈이는 -1씩 뒤로 가서 찾는 조건 밖에 없음
        print(n - k)
        return

    heappush(heap, [0, n]) #출발 node 힙에 넣기
    while heap:
        w, n = heappop(heap)
        for nx in [n + 1, n - 1, n * 2]: #1칸앞으로 , 1칸 뒤로, 순간이동
            if 0 <= nx <= 100000:
                if nx == n * 2 and dp[nx] == inf: #순간이동을 할 거고 방문하지 않았으면
                    dp[nx] = w
                    heappush(heap, [w, nx])
                elif dp[nx] == inf: # 그외에 1씩 앞으로 가줘야할 때 (방문 X)
                    dp[nx] = w + 1
                    heappush(heap, [w + 1, nx])
    print(dp[k])


dijkstra(n, k)

---

🔜[2023.06.15]1753 : 최단경로

• 난이도 : 골드 IV
  

문제

방향그래프가 주어지면 주어진 시작점에서 다른 모든 정점으로의 최단 경로를 구하는 프로그램을 작성하시오. 단, 모든 간선의 가중치는 10 이하의 자연수이다.

입력

첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가 주어진다. 셋째 줄부터 E개의 줄에 걸쳐 각 간선을 나타내는 세 개의 정수 (u, v, w)가 순서대로 주어진다. 이는 u에서 v로 가는 가중치 w인 간선이 존재한다는 뜻이다. u와 v는 서로 다르며 w는 10 이하의 자연수이다. 서로 다른 두 정점 사이에 여러 개의 간선이 존재할 수도 있음에 유의한다.

출력

첫째 줄부터 V개의 줄에 걸쳐, i번째 줄에 i번 정점으로의 최단 경로의 경로값을 출력한다. 시작점 자신은 0으로 출력하고, 경로가 존재하지 않는 경우에는 INF를 출력하면 된다.

예제

#input
5 6
1
5 1 1
1 2 2
1 3 3
2 3 4
2 4 5
3 4 6
#output
0
2
3
7
INF

풀이

from sys import stdin,maxsize
from heapq import heappush, heappop
V,E = map(int, stdin.readline().strip().split())
inf = maxsize
S = int(stdin.readline().strip())
dp = [inf]*(V+1) #방문여부
heap = []
g = [[] for _ in range(V+1)]

def dijkstra(s):
    for _ in range(E): #노드 그래프 초기화
        u,v,w = map(int,stdin.readline().strip().split())
        g[u].append((w,v)) #가중치, 목적지 노드
    
    dp[s]=0 #시작점은 0으로
    heappush(heap,(0,s)) #시작점 heap넣기
    
    while heap:
        c,n = heappop(heap)

        if dp[n] < c: #가중치 크면 업데이트 x
            continue

        for acc_w , nxt in g[n]:
            nxt_w = acc_w + c
            if nxt_w < dp[nxt]:
                dp[nxt] = nxt_w
                heappush(heap , (nxt_w , nxt))

    for i in range(1,V+1):
         print("INF") if dp[i]==inf else print(dp[i])

dijkstra(S)

💃[2023.06.23]1238 : 파티

• 난이도 : 골드 III
  

문제

N개의 숫자로 구분된 각각의 마을에 한 명의 학생이 살고 있다.
어느 날 이 N명의 학생이 X (1 ≤ X ≤ N)번 마을에 모여서 파티를 벌이기로 했다. 이 마을 사이에는 총 M개의 단방향 도로들이 있고 i번째 길을 지나는데 Ti(1 ≤ Ti ≤ 100)의 시간을 소비한다.
각각의 학생들은 파티에 참석하기 위해 걸어가서 다시 그들의 마을로 돌아와야 한다. 하지만 이 학생들은 워낙 게을러서 최단 시간에 오고 가기를 원한다.
이 도로들은 단방향이기 때문에 아마 그들이 오고 가는 길이 다를지도 모른다. N명의 학생들 중 오고 가는데 가장 많은 시간을 소비하는 학생은 누구일지 구하여라.

입력

첫째 줄에 N(1 ≤ N ≤ 1,000), M(1 ≤ M ≤ 10,000), X가 공백으로 구분되어 입력된다. 두 번째 줄부터 M+1번째 줄까지 i번째 도로의 시작점, 끝점, 그리고 이 도로를 지나는데 필요한 소요시간 Ti가 들어온다. 시작점과 끝점이 같은 도로는 없으며, 시작점과 한 도시 A에서 다른 도시 B로 가는 도로의 개수는 최대 1개이다.
모든 학생들은 집에서 X에 갈수 있고, X에서 집으로 돌아올 수 있는 데이터만 입력으로 주어진다.

출력

첫 번째 줄에 N명의 학생들 중 오고 가는데 가장 오래 걸리는 학생의 소요시간을 출력한다.

예제

#input
4 8 2
1 2 4
1 3 2
1 4 7
2 1 1
2 3 5
3 1 2
3 4 4
4 2 3
#output
10

풀이

from sys import stdin, maxsize
from heapq import heappush, heappop
N, M, X = map(int, stdin.readline().strip().split())
inf = maxsize
g = [[] for _ in range(N+1)]
for _ in range(M):
    u, v, w = map(int, stdin.readline().strip().split())
    g[u].append((w, v))
ans = []

def dijkstra(n):
    heap = []
    dp = [inf]*(N+1)
    dp[n] = 0 #시작점
    heappush(heap,(0,n))
    while heap:
        cost,nxt = heappop(heap)
        if dp[nxt]<cost: # 최소값일 때만 업데이트
            continue
        for acc_cost , idx in g[nxt]:
            nxt_cost = acc_cost+cost
            if nxt_cost < dp[idx]:
                dp[idx]=nxt_cost
                heappush(heap,(nxt_cost,idx))
    # 돌아오는 길
    dp2 = [inf]*(N+1)
    dp2[X] = 0 #시작점
    heappush(heap,(0,X))
    while heap:
        cost,nxt = heappop(heap)
        if dp2[nxt]<cost: # 최소값일 때만 업데이트
            continue
        for acc_cost , idx in g[nxt]:
            nxt_cost = acc_cost+cost
            if nxt_cost < dp2[idx]:
                dp2[idx]=nxt_cost
                heappush(heap,(nxt_cost,idx))
    ans.append(dp[X]+dp2[n])

for n in range(1,N+1):
    dijkstra(n)
print(max(ans))

👩‍💻 Refactored

while문을 두번 돌다니..코드가 중복돼잖아..이건 비효율적이야!리팩토링해야겠어!

😊같이 알고리즘 스터디를 하는 팀원이 친절하게 피드백을 제공해주셔서 참고해서 코드를 약간 수정했다.

from sys import stdin, maxsize
from heapq import heappush, heappop
N, M, X = map(int, stdin.readline().strip().split())
inf = maxsize
g = [[] for _ in range(N+1)]
for _ in range(M):
    u, v, w = map(int, stdin.readline().strip().split())
    g[u].append((w, v))
ans = [0 for _ in range(N)] 
def dijkstra(n,otw_back):
    heap = []
    dp = [inf]*(N+1) #중복제거
    start = n if otw_back else X
    dp[start] =0
    heappush(heap,(0,start))
    while heap:
        cost,nxt = heappop(heap)
        if dp[nxt]<cost: # 최소값일 때만 업데이트
            continue
        for acc_cost , idx in g[nxt]:
            nxt_cost = acc_cost+cost
            if nxt_cost < dp[idx]:
                dp[idx]=nxt_cost
                heappush(heap,(nxt_cost,idx))
    return (dp[n],dp[X])

for n in range(1,N+1):
    a = dijkstra(n,False) # 최소경로
    b = dijkstra(n,True) # 돌아오는 길
    ans.append((sum([list(a)[0],list(b)[-1]]))) #두 최소경로를 튜플로 받아왔으니 리스트로 형변환하고 더해줘서 정답 배열에 넣어

print(max(ans)) #최대거리인 학생 print

📝중간 체크

세 문제 풀이한 결과, 반복되는 패턴은
1. vertex과 edge간의 weight 담을 배열 필요
2. 처음 (시작점)을 힙에 넣기 : (weight,연결된 vertex)의 튜플 형태
3. heap에 남는게 없을 때까지 pop해주는데, pop한 값의 weight가 연결된 vertex의 weight보다 큰 경우는 패스
4. for문으로 문제조건 (다음 방문할 노드들)을 순회하면서 해당값이 최소경로 일 때 dp 업데이트하고 heappush해주기

🤸‍♀️[2023.06.24] 1504 : 특정한 최단 경로

• 난이도 : 골드IV
  

문제

방향성이 없는 그래프가 주어진다. 세준이는 1번 정점에서 N번 정점으로 최단 거리로 이동하려고 한다. 또한 세준이는 두 가지 조건을 만족하면서 이동하는 특정한 최단 경로를 구하고 싶은데, 그것은 바로 임의로 주어진 두 정점은 반드시 통과해야 한다는 것이다.
세준이는 한번 이동했던 정점은 물론, 한번 이동했던 간선도 다시 이동할 수 있다. 하지만 반드시 최단 경로로 이동해야 한다는 사실에 주의하라. 1번 정점에서 N번 정점으로 이동할 때, 주어진 두 정점을 반드시 거치면서 최단 경로로 이동하는 프로그램을 작성하시오.

입력

첫째 줄에 정점의 개수 N과 간선의 개수 E가 주어진다. (2 ≤ N ≤ 800, 0 ≤ E ≤ 200,000) 둘째 줄부터 E개의 줄에 걸쳐서 세 개의 정수 a, b, c가 주어지는데, a번 정점에서 b번 정점까지 양방향 길이 존재하며, 그 거리가 c라는 뜻이다. (1 ≤ c ≤ 1,000) 다음 줄에는 반드시 거쳐야 하는 두 개의 서로 다른 정점 번호 v1과 v2가 주어진다. (v1 ≠ v2, v1 ≠ N, v2 ≠ 1) 임의의 두 정점 u와 v사이에는 간선이 최대 1개 존재한다.

출력

첫째 줄에 두 개의 정점을 지나는 최단 경로의 길이를 출력한다. 그러한 경로가 없을 때에는 -1을 출력한다.

예제

#input
4 6
1 2 3
2 3 3
3 4 1
1 3 5
2 4 5
1 4 4
2 3
#output
7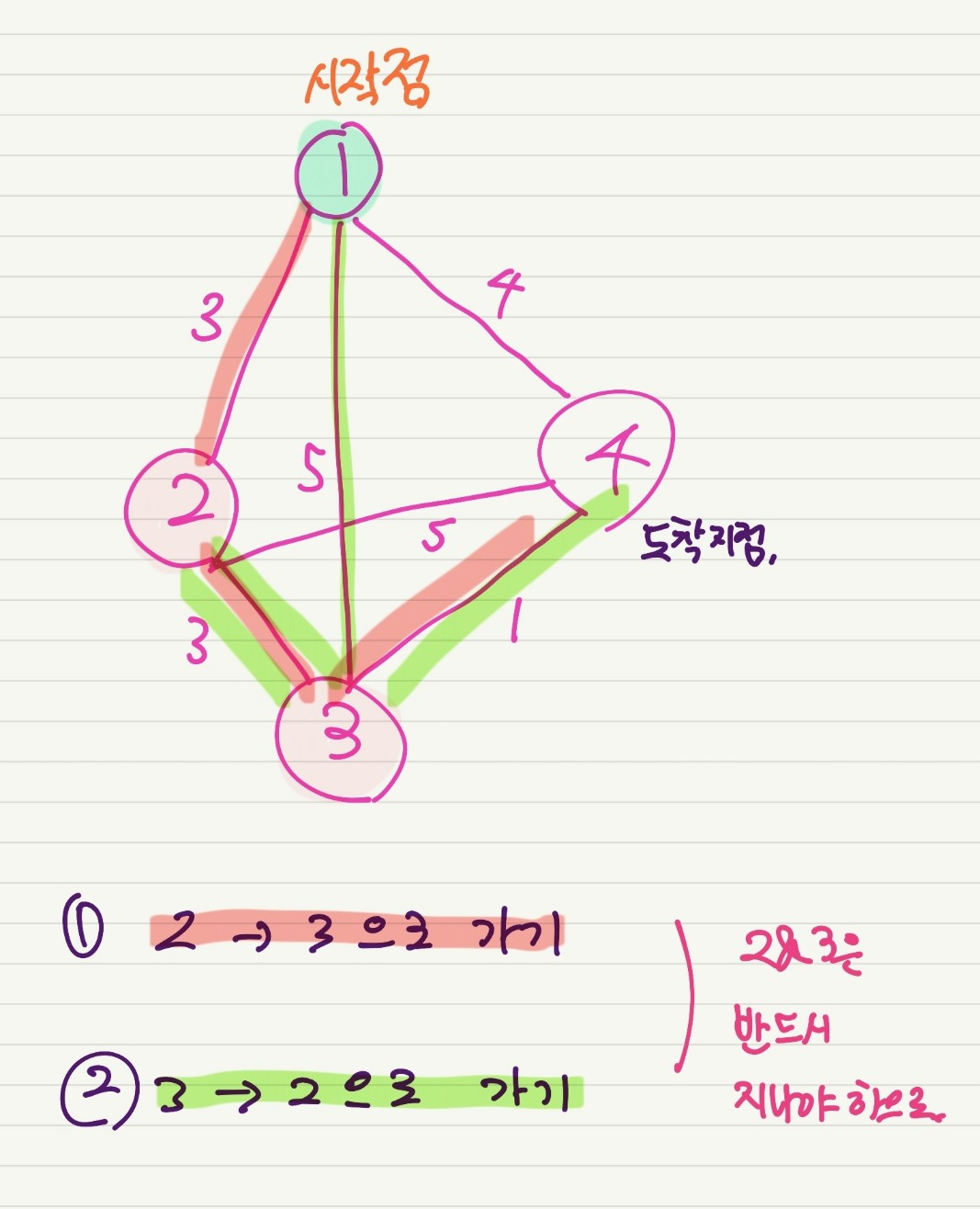

😂 문제를 잘못 이해해서 그랬네
오해 : 1 ~ N까지 vertex를 두 지점 모두 건너서 가는 경우 중 최단거리를 구해야한다고 생각
정정 : 위의 그림처럼 N에 도착점에 도달할 때까지 꼭 건너야하는 두 지점 포함 최단 거리 구하기

풀이

# a와 b 사이의 양방향 길,
# 다시 갈 수는 있지만 꼭 건너야하는 지점은 거치고
# 최소 경로로 가야함
from sys import stdin,maxsize
from heapq import heappop, heappush
N, E = map(int, stdin.readline().strip().split())
inf =maxsize
g = [[] for _ in range(N+1)]
for _ in range(E):
    a,b,c = map(int, stdin.readline().strip().split())
    g[a].append((c,b))
    g[b].append((c,a))
v1,v2 = map(int, stdin.readline().strip().split())

def dijkstra(n):
    heap = []
    dp =[inf]*(N+1)
    dp[n]=0
    heappush(heap,(0,n))
    while heap:
        cst, nxt = heappop(heap)
        if dp[nxt]<cst:
            continue
        for acc_c , idx in g[nxt]:
            nxt_c = acc_c+cst
            if nxt_c < dp[idx]:
                dp[idx] = nxt_c
                heappush(heap,(nxt_c,idx))
    return dp

# 아래부부은 도저히 30분 안에 생각이 안나서 코드들을 참고해서 작성. (이해를 잘못했었네..ㅋㅋㅋ)
# 파티 문제 리팩토링하는데 참고가 되었다.
s1 = dijkstra(1) #start 1, 1에서 시작했을 때 최소경로
sv1 = dijkstra(v1) #start v1, 반드시 지나야하는 첫번째 vertex에서 시작했을 때 최소경로
sv2 = dijkstra(v2) #start v2, 반드시 지나야하는 두번째 vertex에서 시작했을 때 최소경로

# 각 경로의 합들
v1_route = s1[v1]+sv1[v2]+sv2[N] 
v2_route = s1[v2]+sv1[N]+sv2[v1]

# 2 -> 3으로 가는 방향 vs 3->2로 가는 방향 중 최소값 출력, 없다면 -1
ans = min(v1_route,v2_route)
print(ans if ans<inf else -1) 

references

wikipedia : Dijkstra algorithm