[알고리즘] 선택 정렬(Selection Sort)

📝 선택 정렬(Selection Sort)

• 해당 자리를 선택하고 그 자리에 오는 값을 찾는 것
• 현재 위치에 저장될 값의 크기가 작냐, 크냐에 따라서 최소 선택 정렬(오름차순 정렬)과 최대 선택 정렬(내림차순 정렬)로 나뉜다.

📝 개념(오름차순)

• 1회전에서는 맨 앞의 값을 기준으로 하고 배열에서 최솟값을 찾은 후 이것을 맨 앞의 값과 교체한다.
• 2회전에서는 두 번째 값을 기준으로 하고 기준 이후의 원소들 중에서 최솟값을 찾은 후 이것을 기준에 위치한 값과 교체한다.
• 이후에도 기준의 앞부분에 위치한 원소들은 제외하고 기준의 뒷부분에 위치한 원소들 중 최솟값을 찾아 교체해준다.

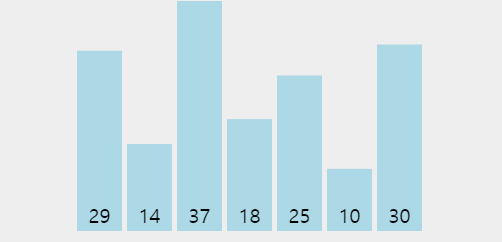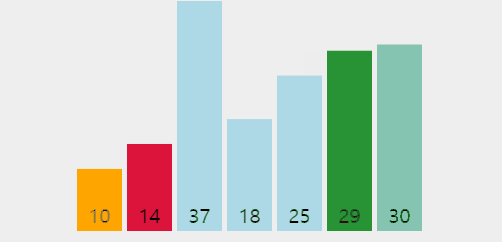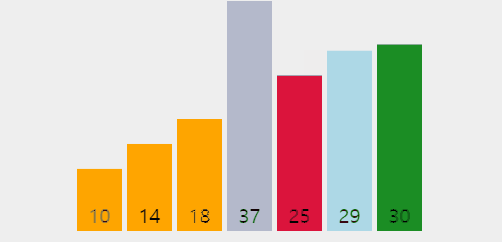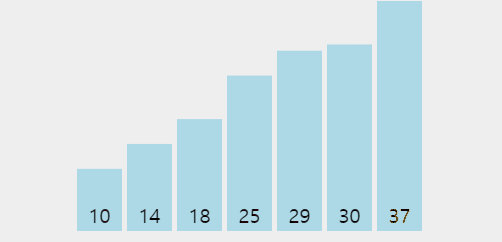
👆 위 짤에서 1회전 시 10이 맨 앞에 오고 2회전 시에는 14가, 이런 식으로 진행됨을 볼 수 있다.

💾 Java코드

private static void sort(int[] arr) {
	for (int i = 0; i < arr.length; i++) { 			// 1️⃣
            int index = i;
            for (int j = i + 1; j < arr.length; j++) {		// 2️⃣
                if (arr[j] < arr[index]) {			// 3️⃣
                	index = j;
                }
            }
          	
          							// 4️⃣
            int temp = arr[index];
            arr[index] = arr[i];
            arr[i] = temp;

        }
    }

1. ① for 기준을 선택하는 반복문이다. 1회전때에는 맨 앞의 값이 기준이고 그 다음, 그 다음 순으로 기준이 넘어가므로 i를 주어진 배열의 길이까지 1씩 증가시킨다.
2. ②의 for문은 기준 이후의 원소들을 비교해야 하기 때문에 기준(i)를 제외해야 하므로 i+1부터 주어진 배열의 길이까지 1씩 증가시킨다.
3. ③의 if문은 최솟값의 위치를 알아야 하기 때문에 arr[j]가 arr[index]보다 작다면 index를 j 값으로 바꾸어준다.
4. ④는 최솟값의 위치인 index를 구했으므로 기준에 위치한 원소와 index에 위치한 원소를 교환한다.

📝 특징

• 장점

  • 단순한 알고리즘(자료 이동 횟수가 미리 결정된다.)
  • 비교는 여러번이지만 실제 교환 횟수는 적기 때문에 비교적 효율적이다.
  • 배열 안에서 정렬하는 방식이므로, 다른 메모리 공간을 필요로 하지 않는다.
  • 버블 정렬과 비슷하지만 조금 더 빠르다.

• 단점

  • 시간복잡도가 최악, 최선, 평균 모두 O(n^2) 으로, 굉장히 비효율적입니다.
  • 불안정 정렬(Unstable Sort)이다.

📝 시간 복잡도

(n-1) + (n-2) + .... + 2 + 1 = n(n-1)/2이므로, O(N^2) 이다. 최선, 평균, 최악 모든 경우의 시간복잡도가 O(N^2) 이다.

📝 공간 복잡도

주어진 배열 안에서 교환을 통해 정렬이 수행되므로 O(N)이다.