01. 자동 미분

텐서플로의 자동 미분

tf.GradientTape

tf.GradientTape는 컨텍스트(context) 안에서 실행된 모든 연산을 테이프(tape)에 "기록".
그 다음 텐서플로는 후진 방식 자동 미분(reverse mode differentiation)을 사용해 테이프에 "기록된" 연산의 그래디언트를 계산합니다.

Scalar 를 Scalar로 미분

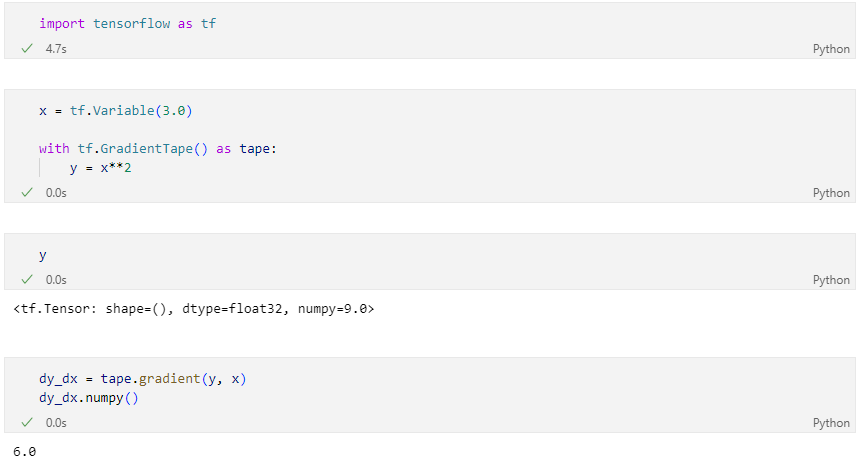
Scalar를 Vector로 미분

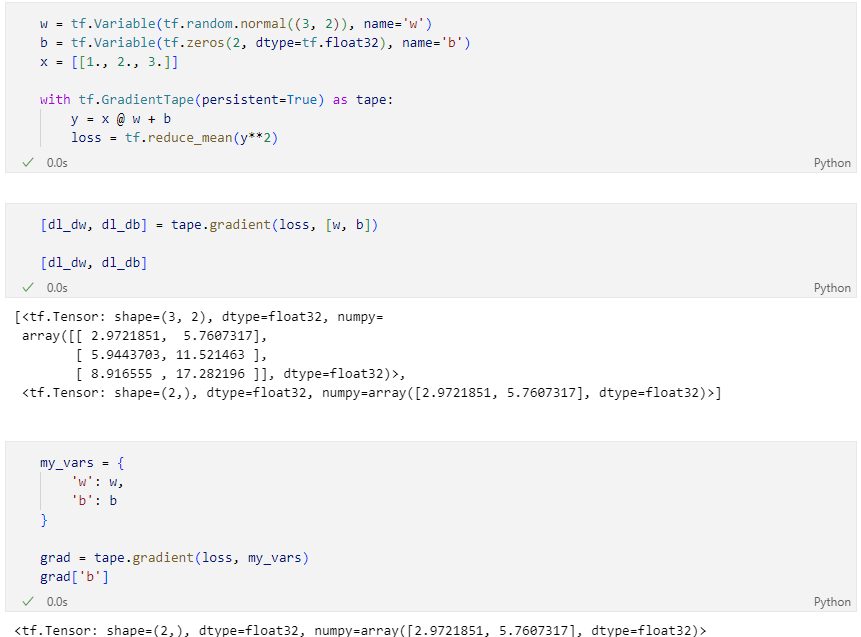
자동미분 컨트롤

• tf.Variable만 기록
• A variable + tensor 는 tensor를 반환
• trainable 조건으로 미분 기록을 제어

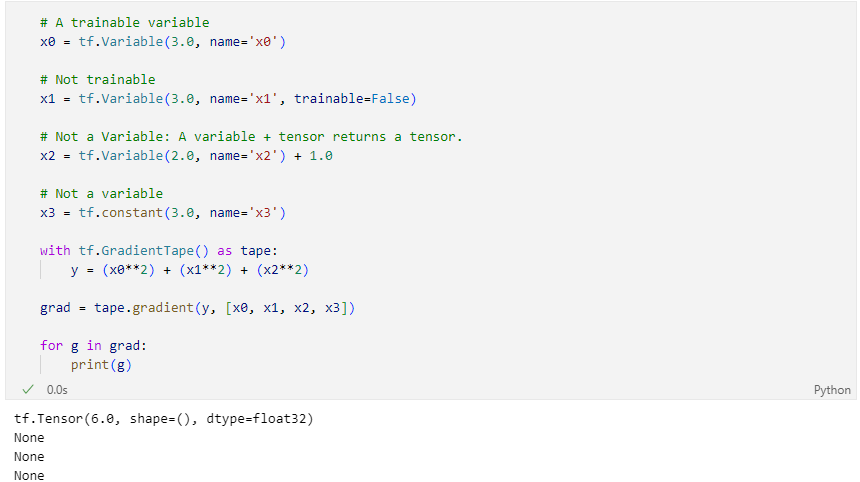
기록되고 있는 variable 확인하기

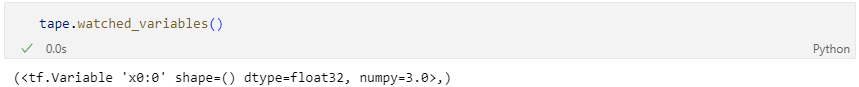
02. Linear Regression

linear regression 구현

Dataset

가상 데이터셋 생성

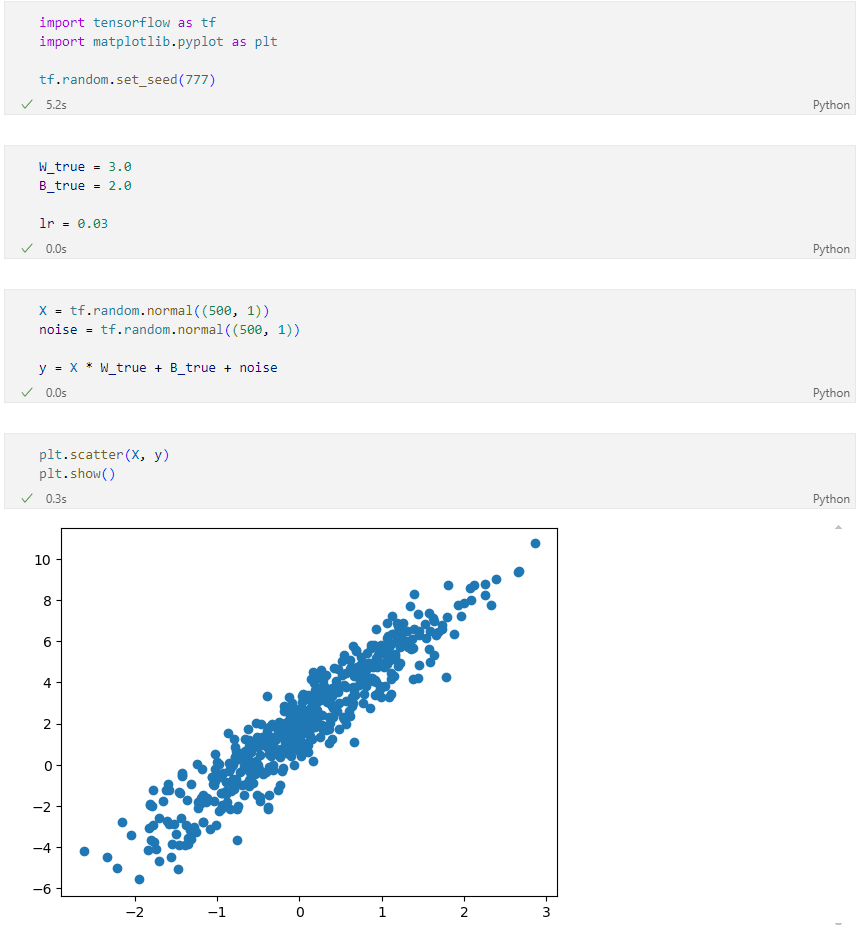
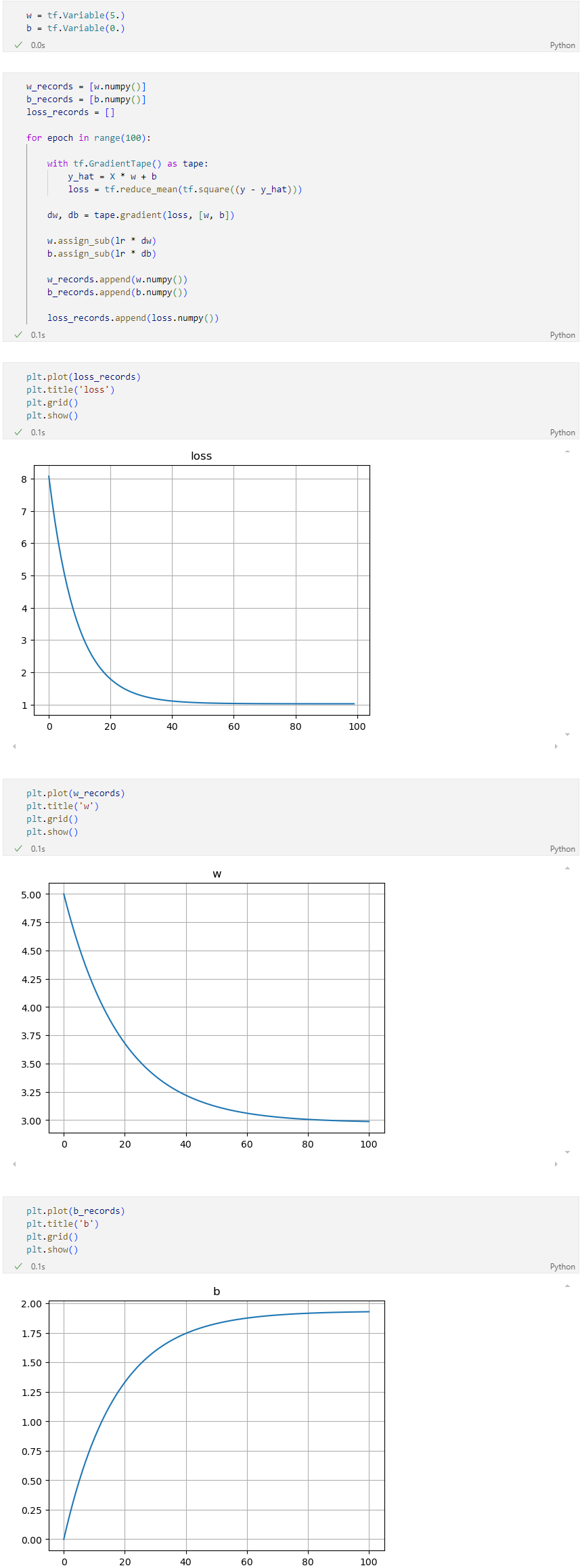
자동 미분 및 시각화

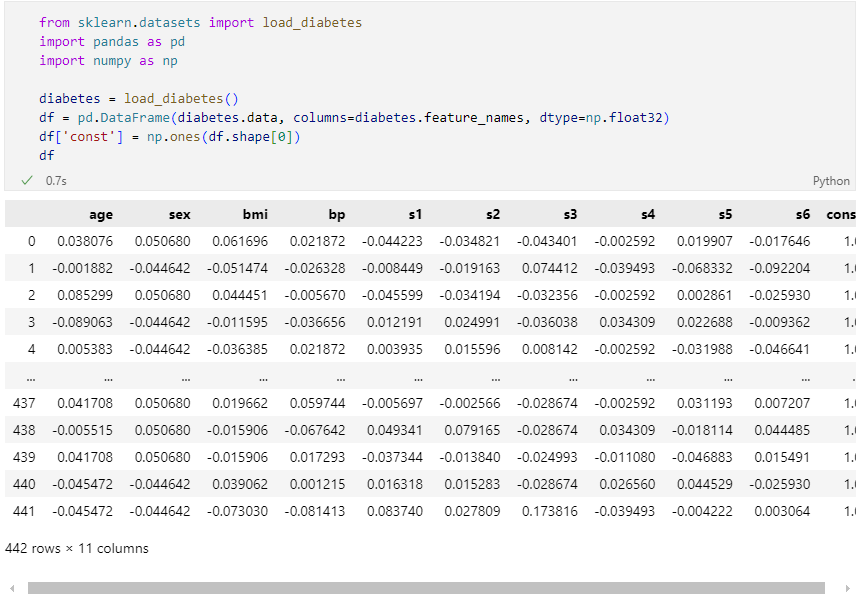
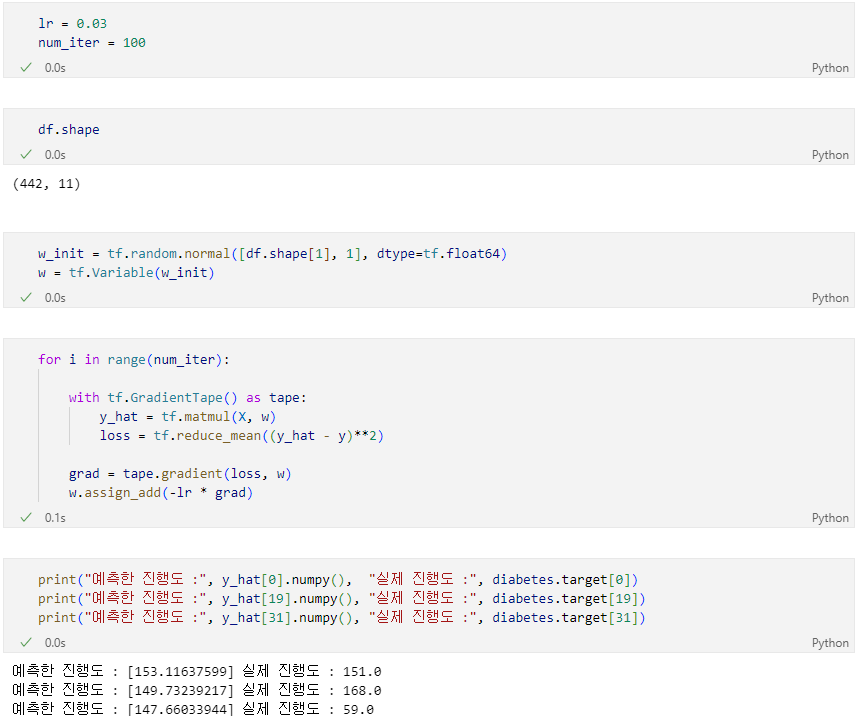
Dataset 당뇨병 진행도 예측 하기

$w$ 의 추정치

$X$를 Feature, $w$를 가중치 벡터, $y$를 Target이라고 할 때,
$X^T X$의 역행령이 존재 한다고 가정했을 때,
아래의 식을 이용해 $w$의 추정치 $w^*$를 구해봅시다.

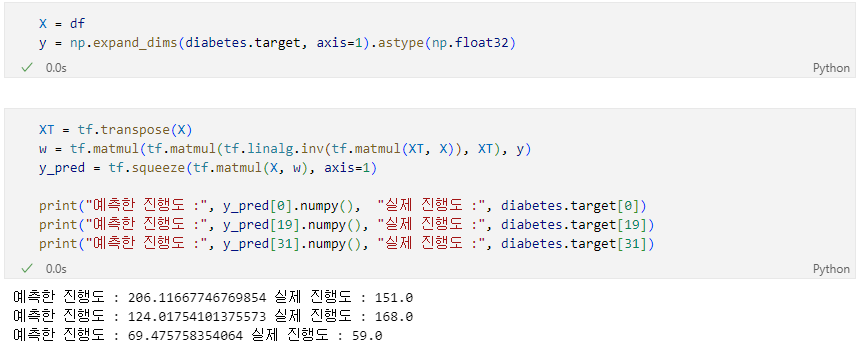
SGD 방식으로 구현

• Conditions
  • steepest gradient descents(전체 데이터 사용)
  • 가중치는 Gaussian normal distribution에서의 난수로 초기화함.
  • step size == 0.03
  • 100 iteration

03. perceptron

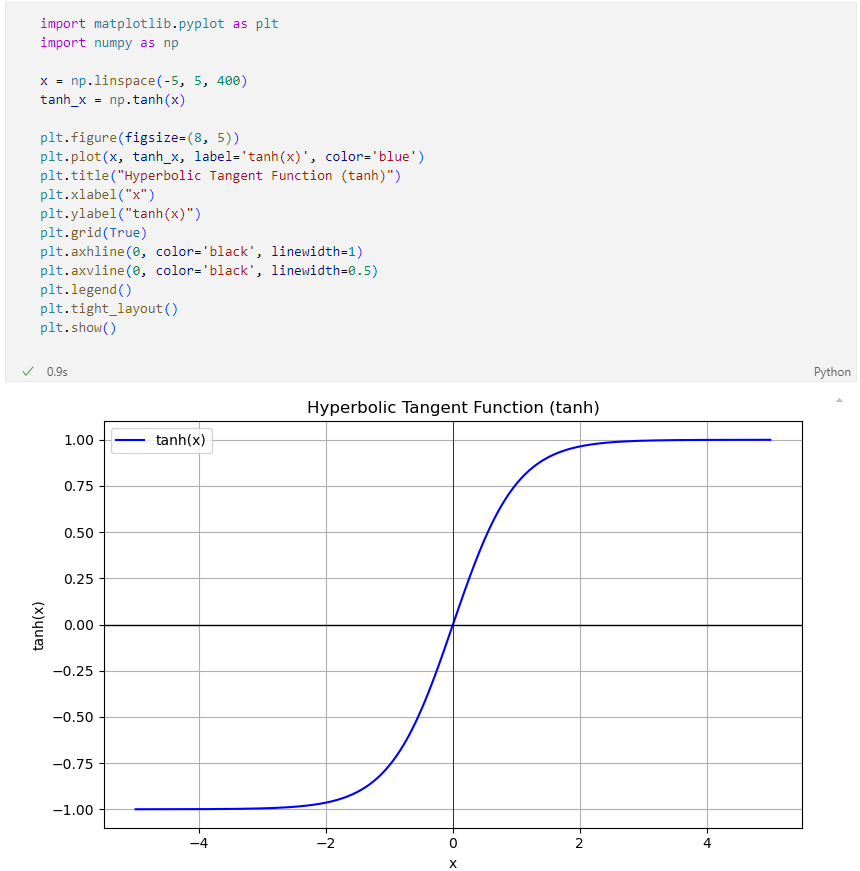
tanh + hinge loss

이번엔 Iris 데이터 중 두 종류를 분류하는 퍼셉트론을 제작한다. y값은 1 또는 -1을 사용하고 활성화 함수로는 하이퍼탄젠트(hypertangent)함수를 사용한다.

비용 함수로는 다음 식을 사용한다.
(예측값이 정답과 일치하지 않을 때만 손실이 발생)

hypertangent

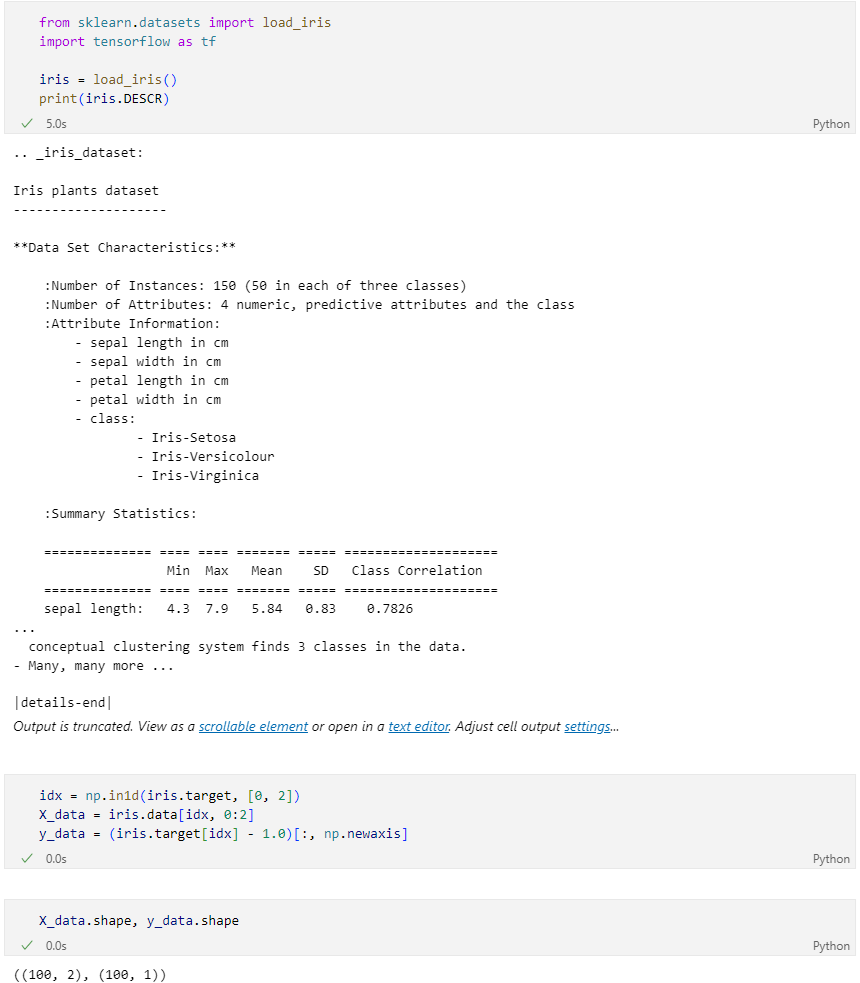
iris_dataset load

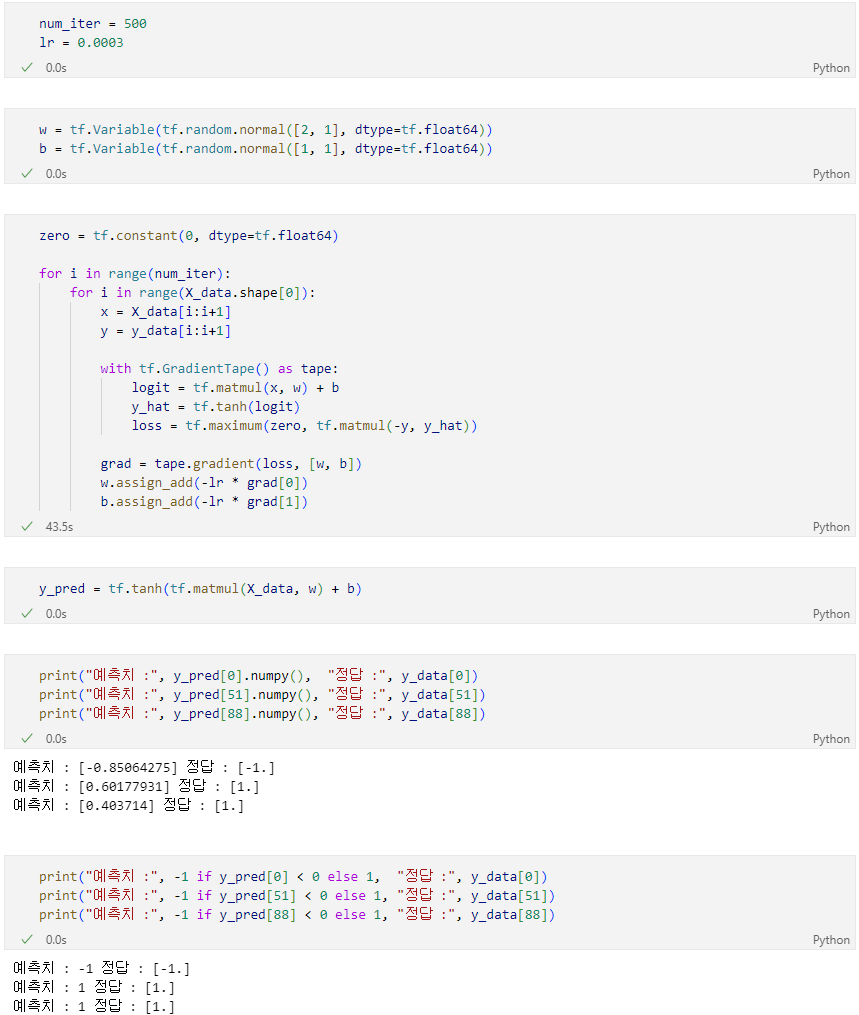
SGD

• 데이터 하나당 한번씩 weights 업데이트
• step size = 0.0003
• iteration = 200

Batch 버전

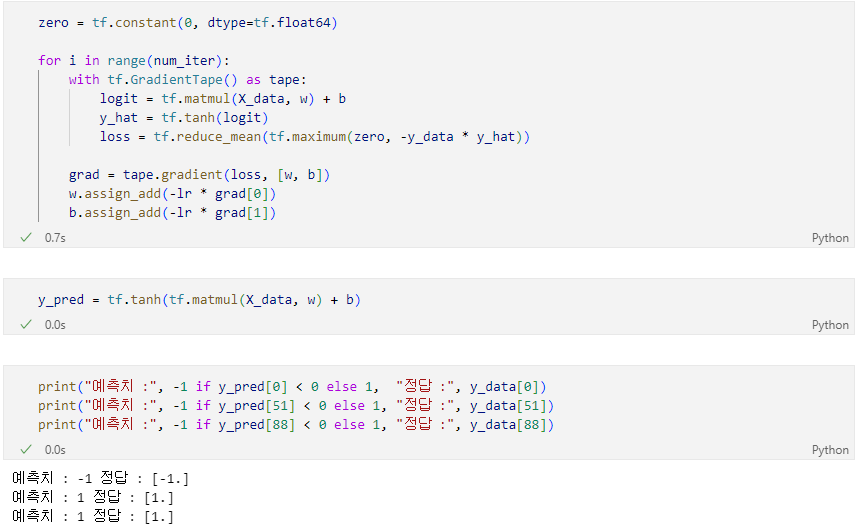
SGD vs Batch 버전

항목	SGD	Batch 버전
입력 처리	X_data[i:i+1]	X_data 전체 사용
손실 계산	샘플 1개씩	전체 평균 손실 사용 (reduce_mean)
성능	느리지만 노이즈 많아 일반화 잘됨	빠르고 안정적 (but 메모리 많이 씀)

Mini-batch 버전

항목	설명
batch_size	한 번에 처리할 샘플 수 (예: 16개)
shuffle	데이터 순서를 섞어서 일반화 성능 향상
start:end 슬라이싱	배치 단위로 데이터 분할
reduce_mean	배치 손실 평균 계산

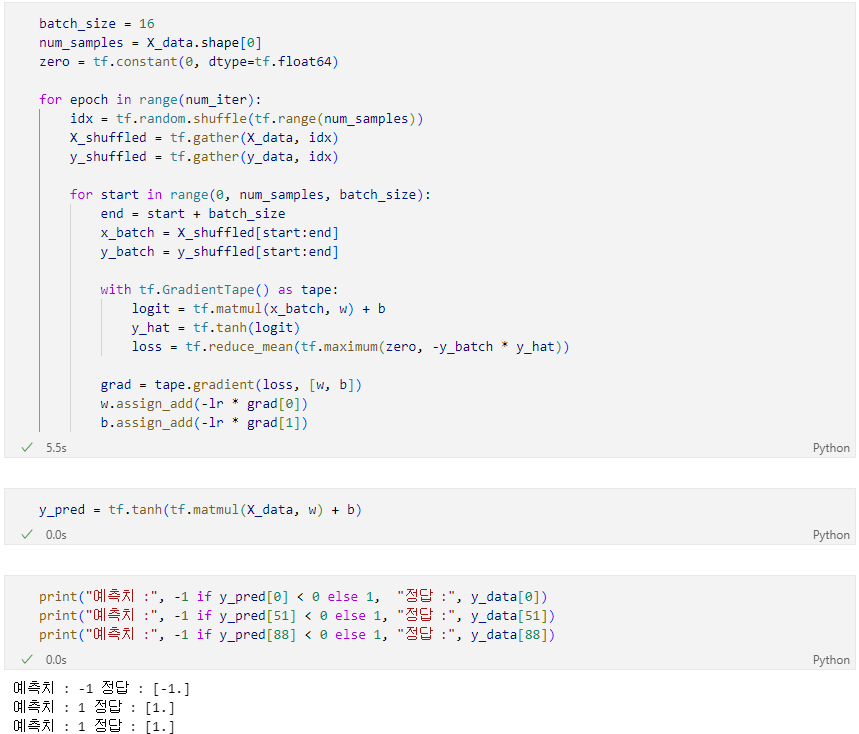
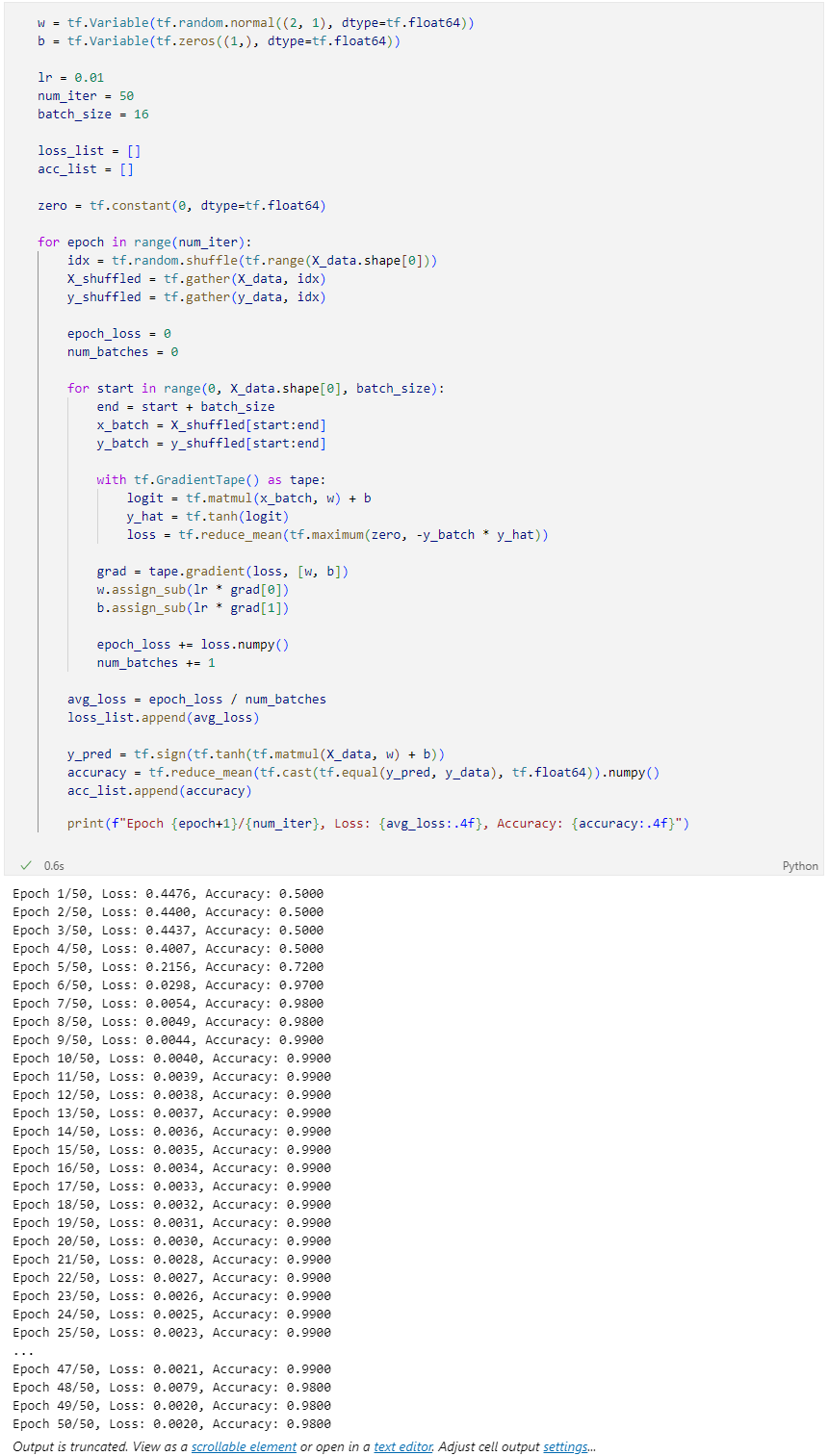
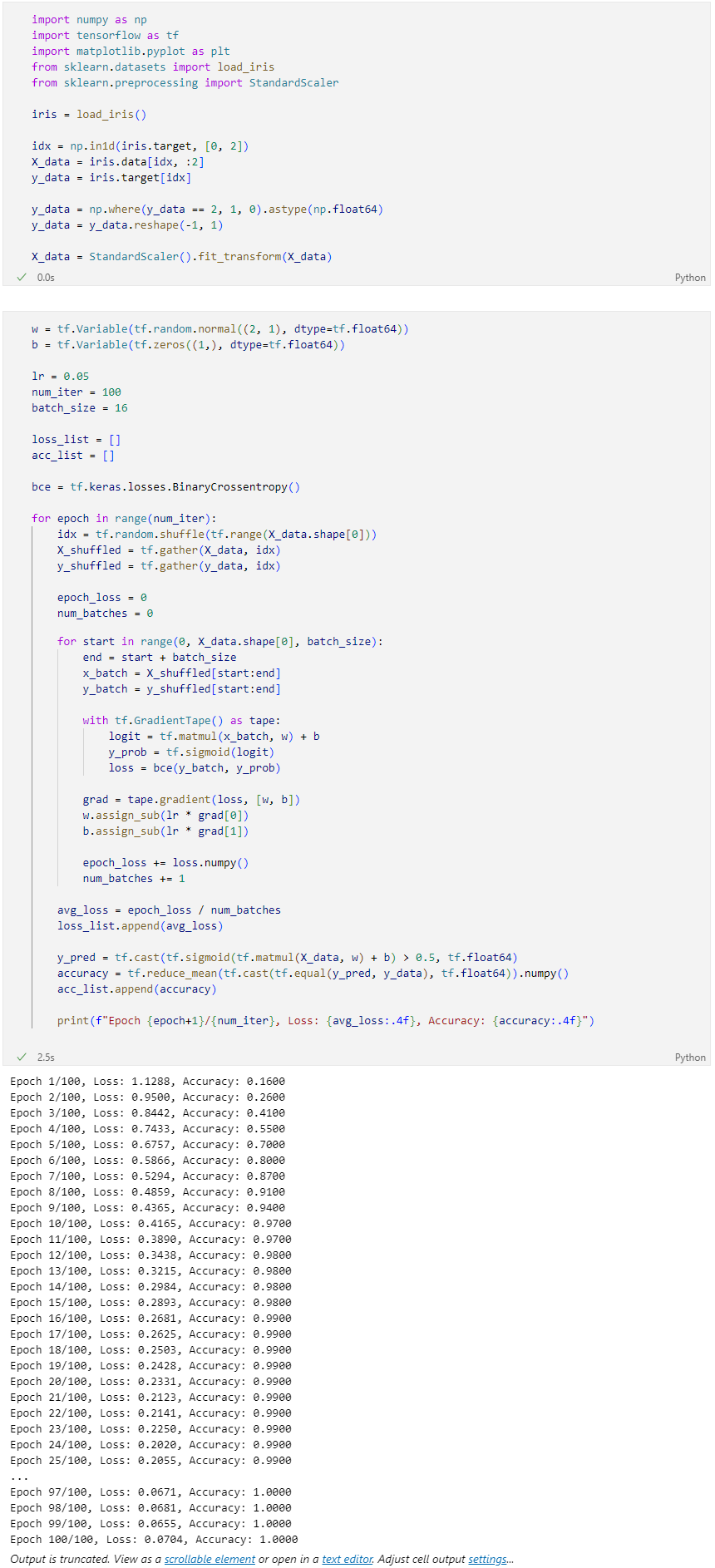
전체 코드 (학습 + 평가 + 시각화 포함)

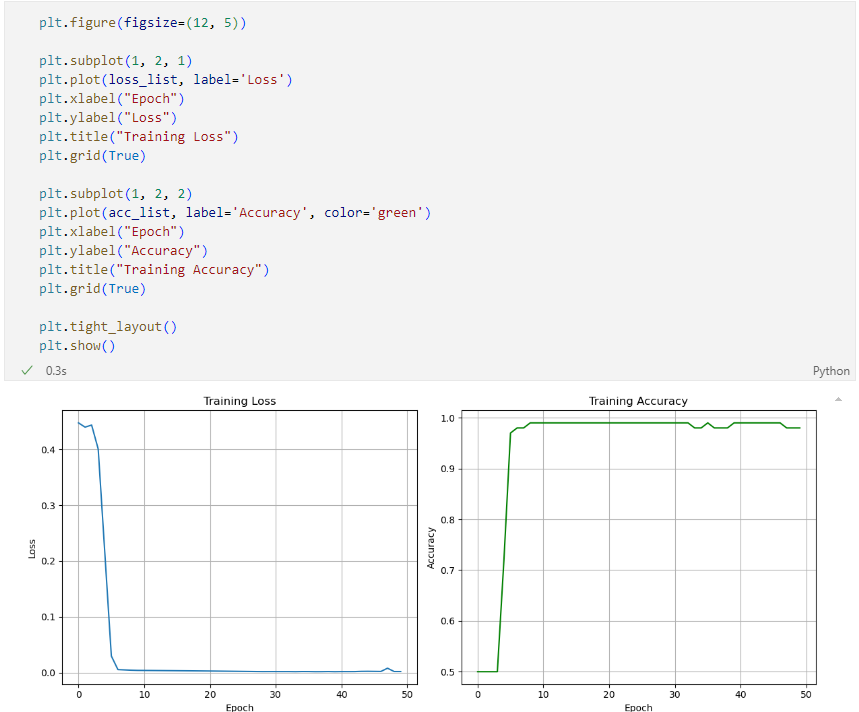
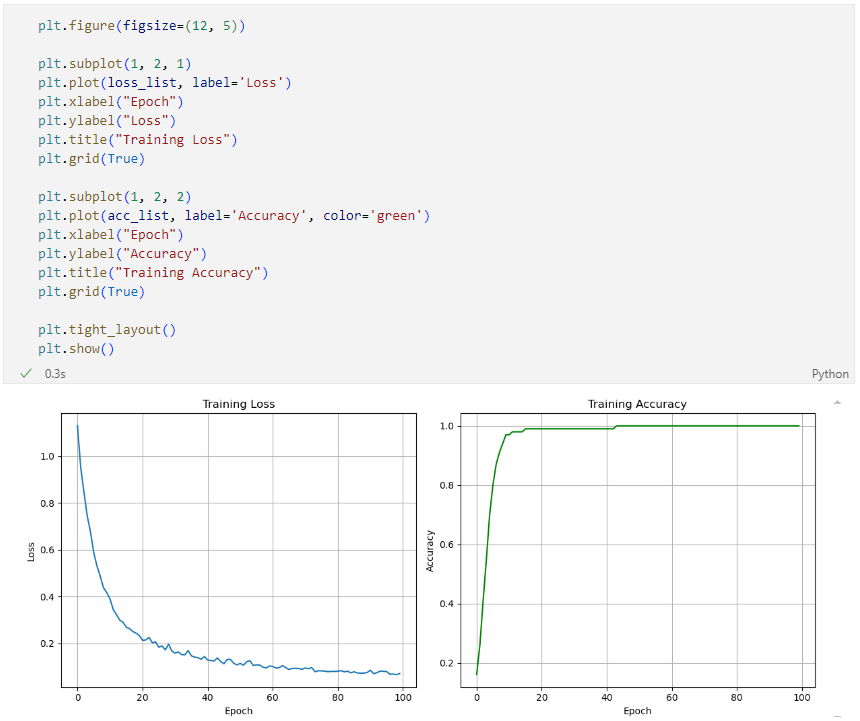
손실과 정확도 시각화

sigmoid + binary cross-entropy

전체 코드

손실과 정확도 시각화

hinge+tanh vs BCE+sigmoid

변경 항목	hinge + tanh	BCE + sigmoid
출력 함수	tanh(w^T x + b)	sigmoid(w^T x + b)
손실 함수	hinge loss (max)	binary cross-entropy
레이블 값	{-1, +1}	{0, 1}
예측 해석 방식	부호 기반	확률 기반 (0.5 기준 분류)