PCA란?

간단한 PCA의 개념
- 차원축소(dimensionality reduction)와 변수추출(feature extraction) 기법으로
널리 쓰이고 있는 주성분분석(Principal Component Analysis) - PCA는 데이터의 분산(variance)을 최대한 보존하면서 서로 직교하는 새 기저(축)를 찾아,
고차원 공간의 표본들을 선형 연관성이 없는 저차원 공간으로 변환하는 기법 - 변수추출(Feature Extraction)은 기존 변수를 조합해 새로운 변수를 만드는 기법
(변수선택(Feature Selection)과 구분할 것)
벡터를 이용해서 데이터를 다시 표현
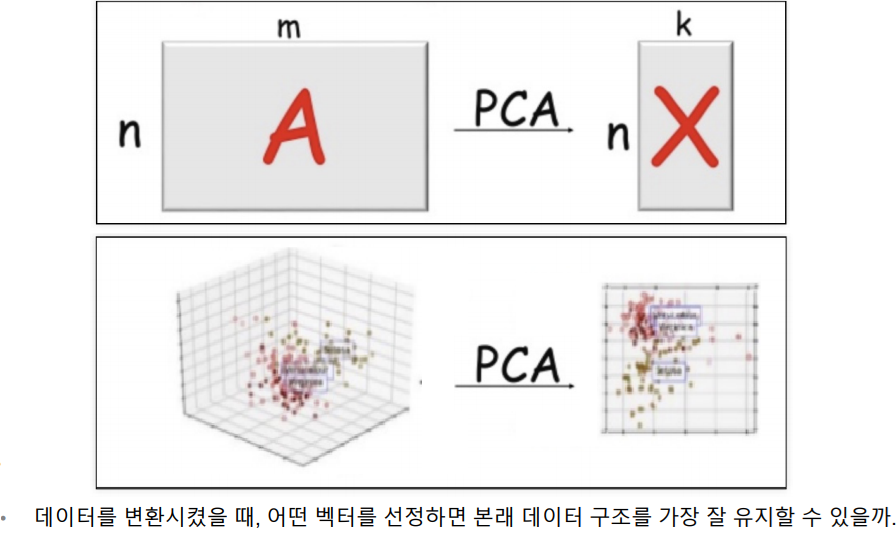
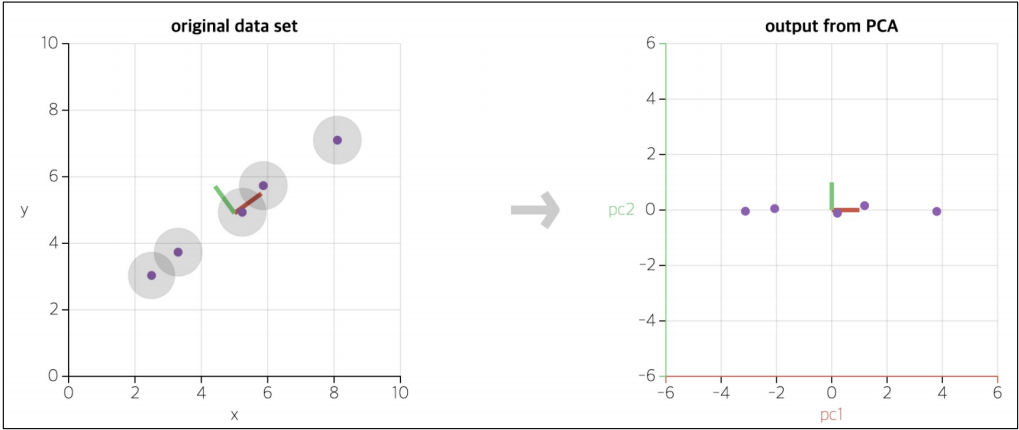
데이터를 새로운 축으로 표현
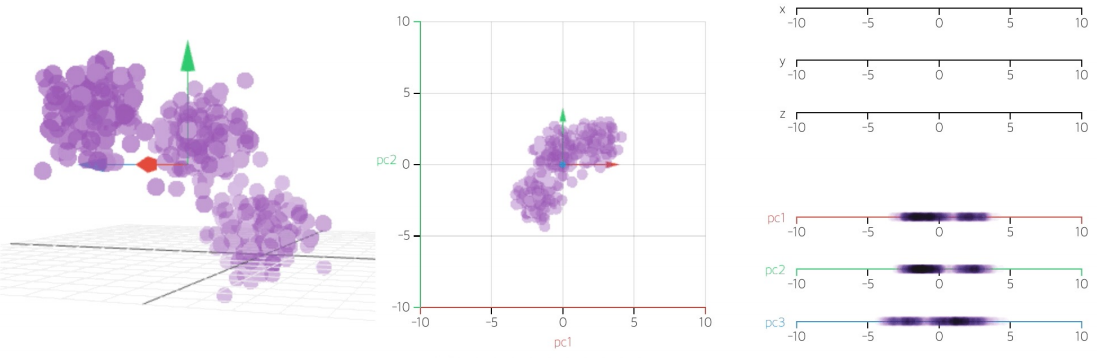
차원이 많은 경우 간단하게 표현
sklearn을 이용한 실습
간단한 실습 데이터 생성
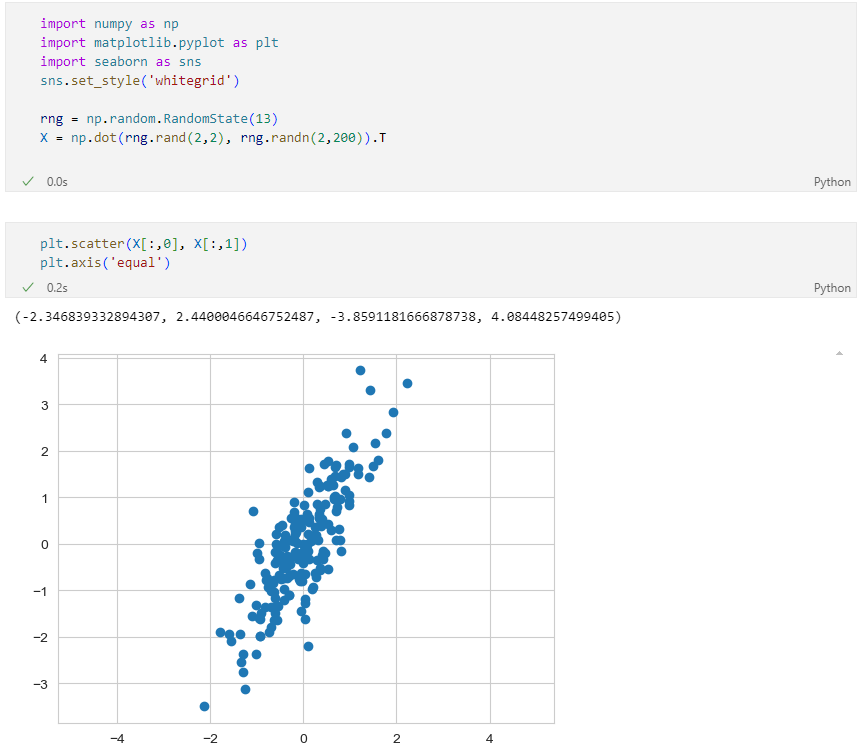
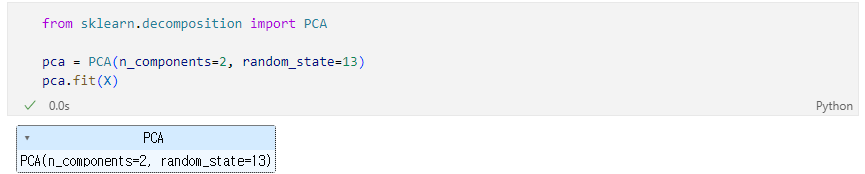
Fit
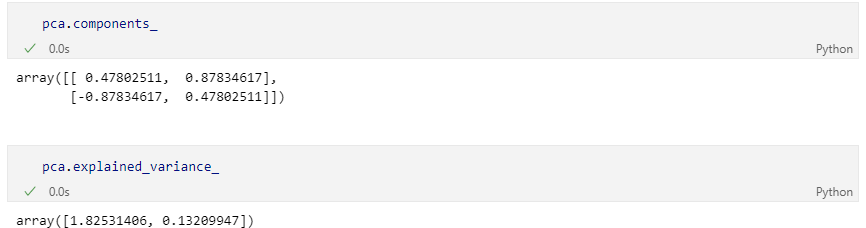
벡터와 분산값
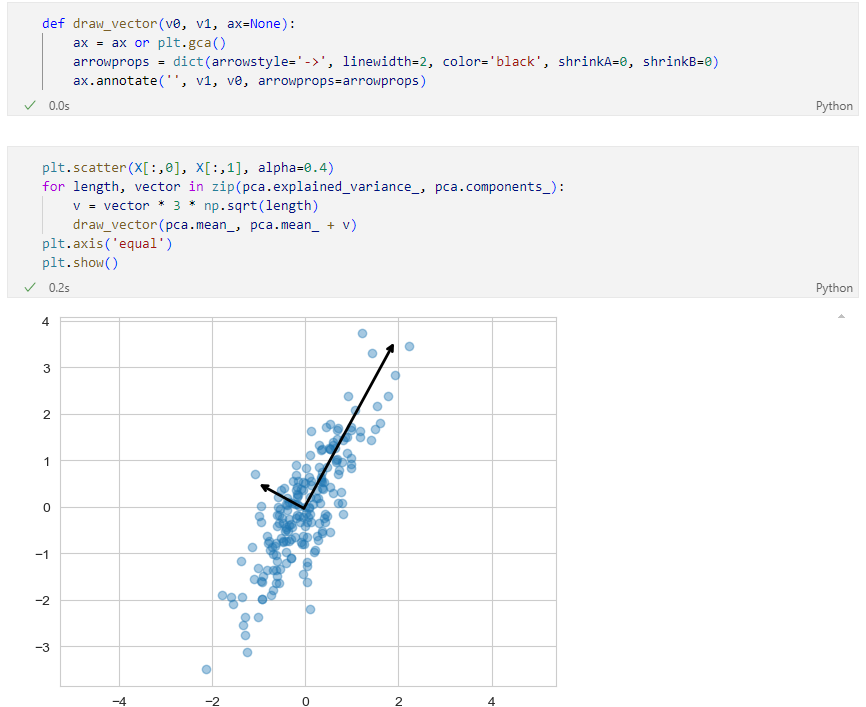
주성분 벡터를 그리기
데이터의 주성분을 찾은 다음 주축을 변경하는 것도 가능
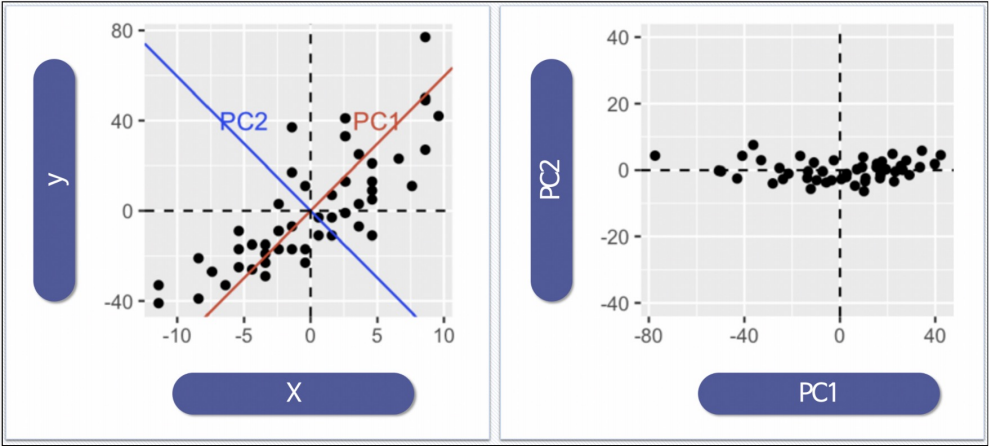
n_components = 1
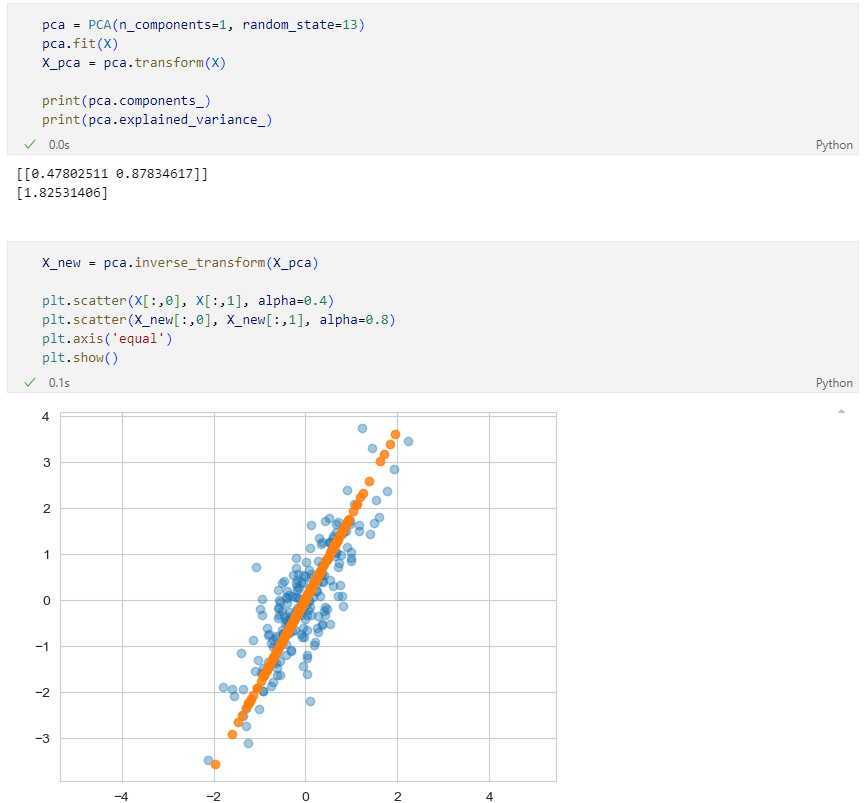
Iris data를 이용한 실습
실습 데이터
특성 4개를 한 번에 확인하기 어려움
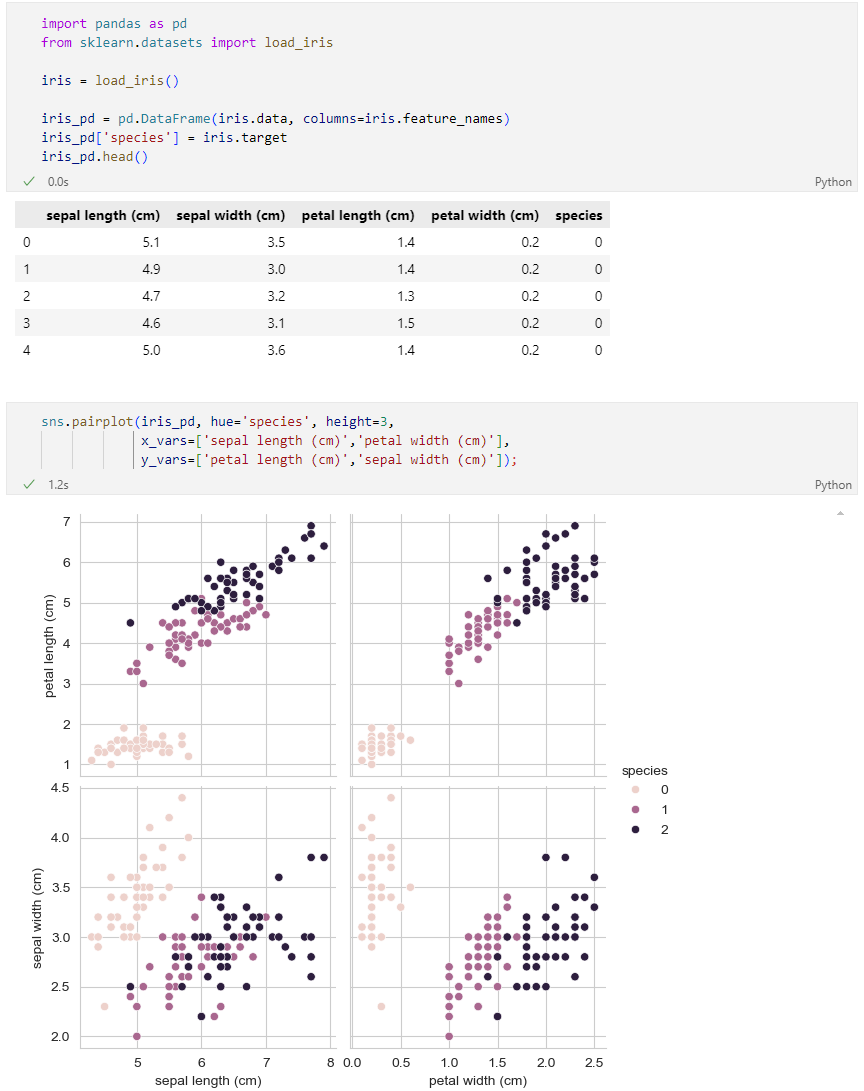
Scaler를 적용
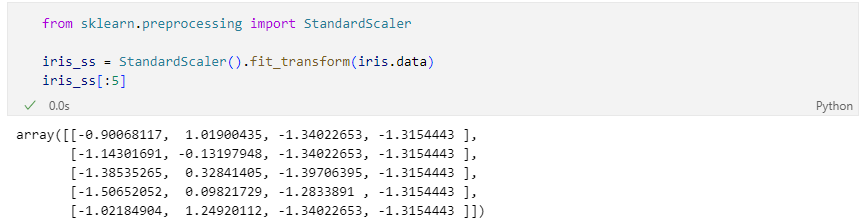
pca 결과를 return하는 함수 적용 후 return값 확인
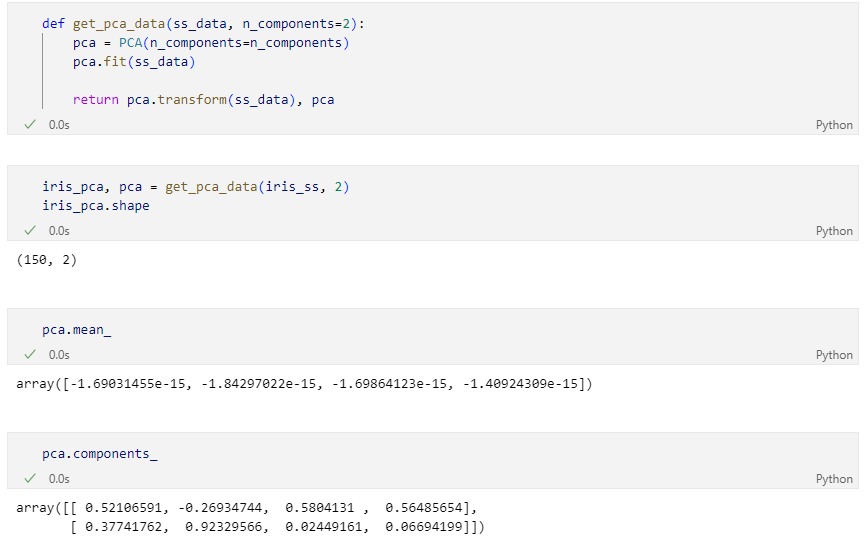
pca가 적용된 결과

4개의 특성을 두 개의 특성으로 정리(pca 결과를 pandas로 정리)
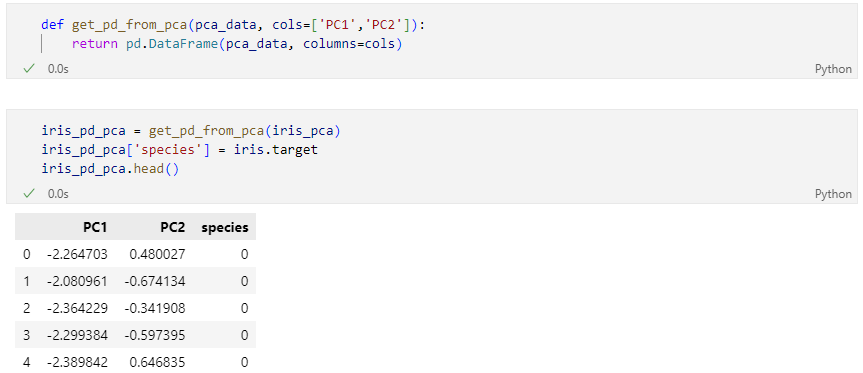
두 개의 특성 표현
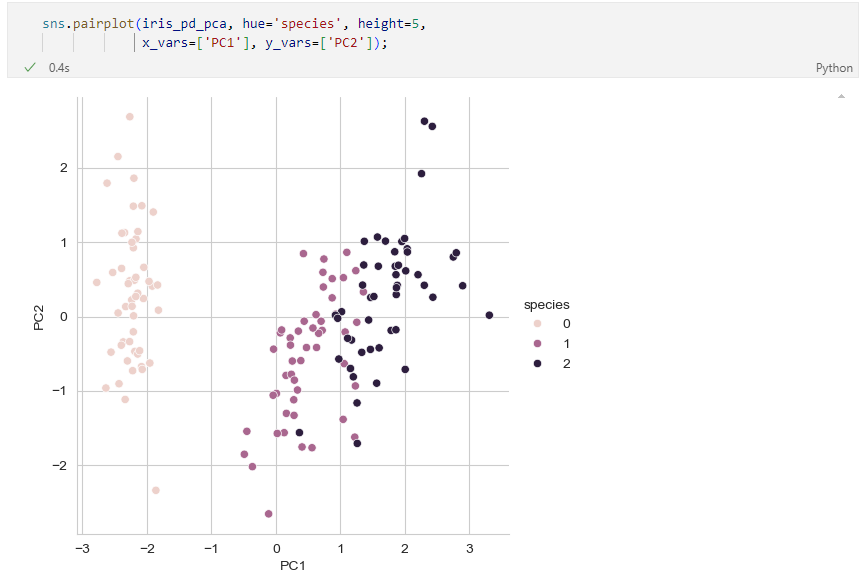
주성분 분석의 위력
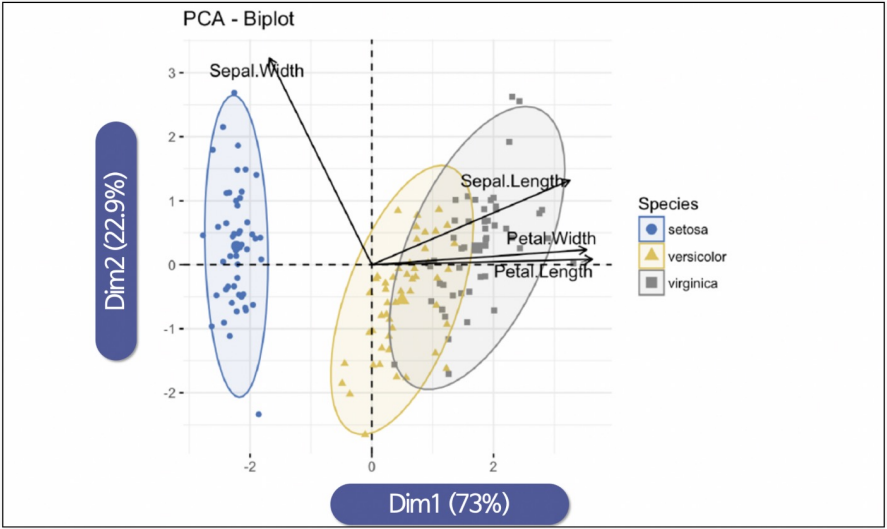
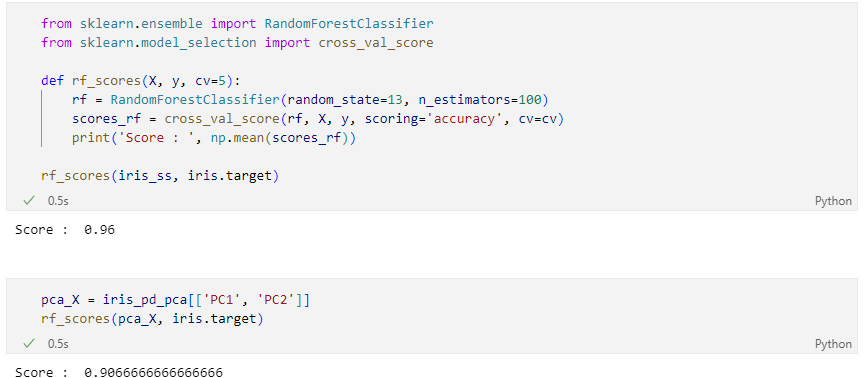
4개 & 2개 특성을 사용해서 randomforest에 적용
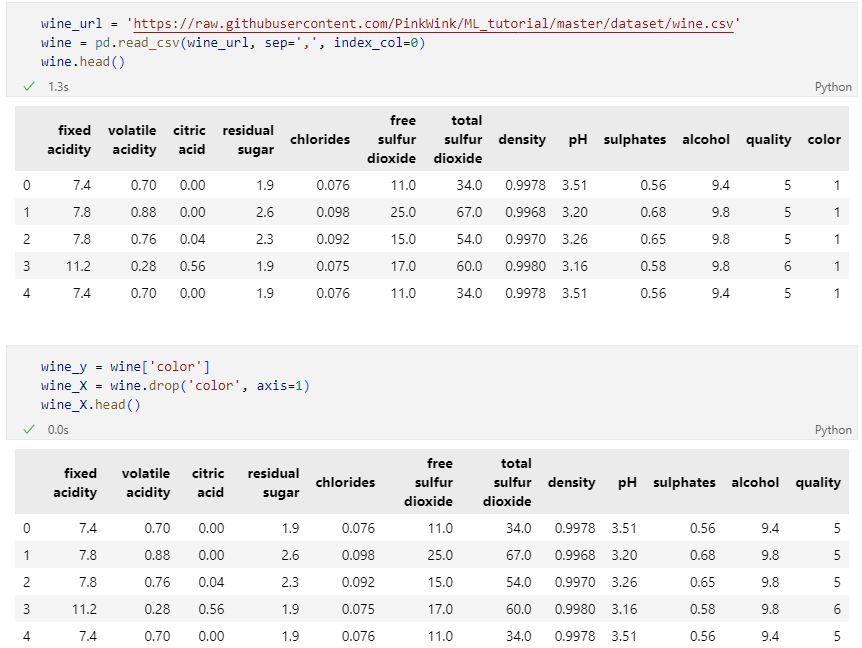
wine data를 이용한 실습
실습 데이터
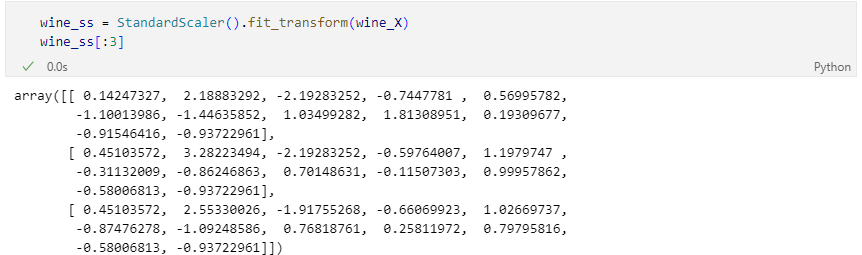
StandardScaler 적용
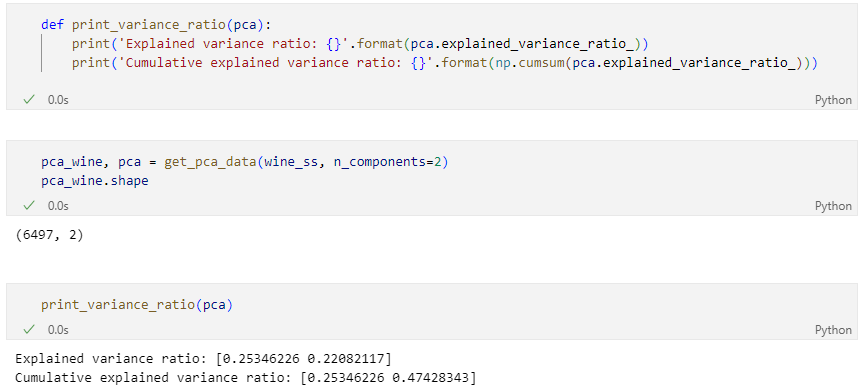
두 개의 주성분으로 줄이는 건 데이터의 50%가 안됨
두 개의 주성분 그리기
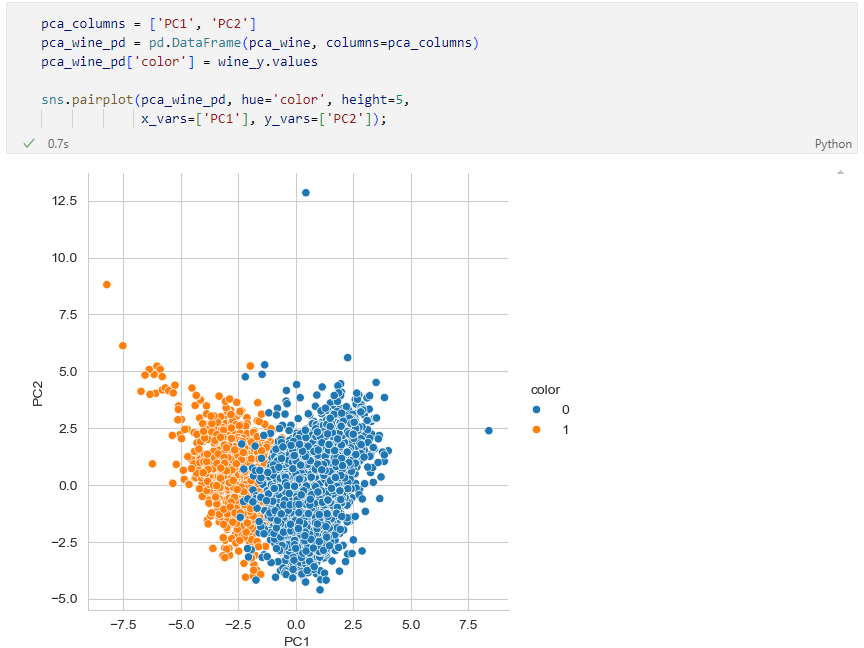
Random Forest에 적용했을 때 원 데이터와 큰 차이가 없다

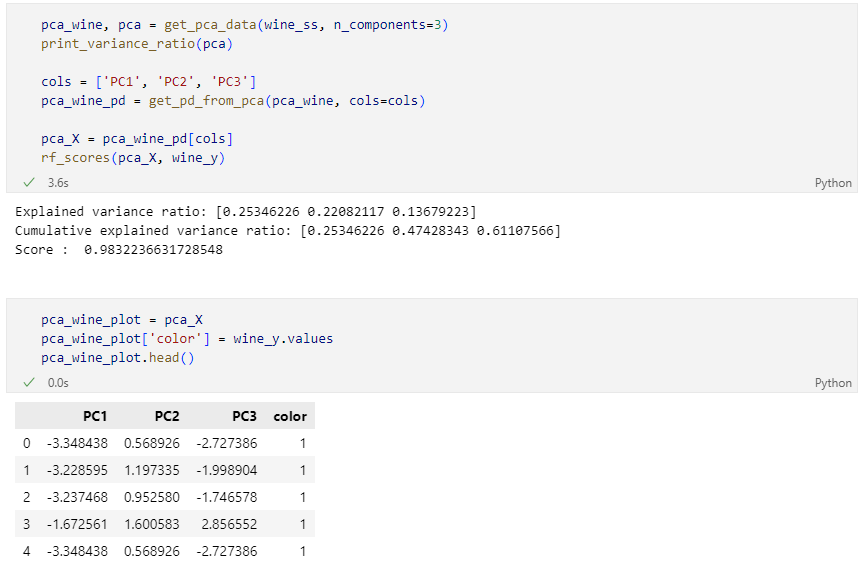
주성분 3개로 표현
주성분 3개로 표현해달라고 했더니, 98% 이상을 표현할 수 있다
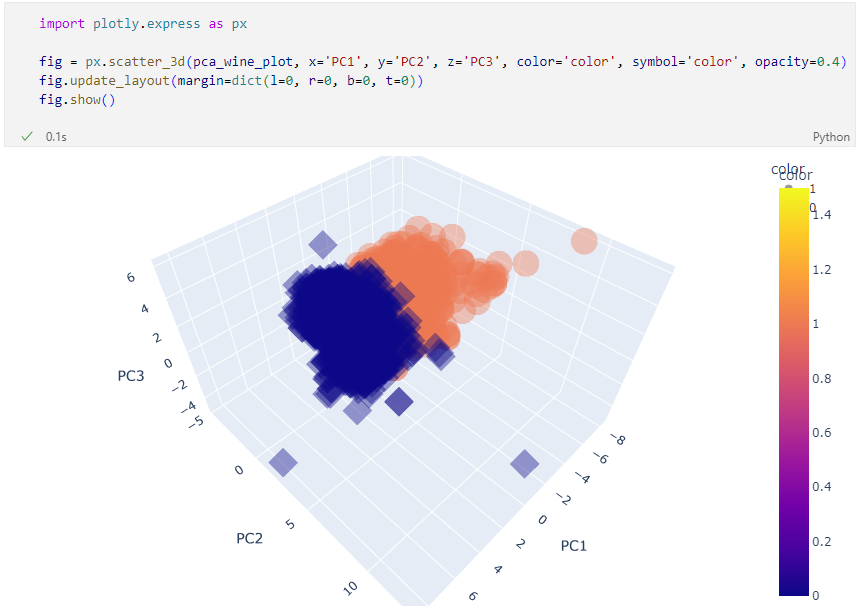
3D로 시각화
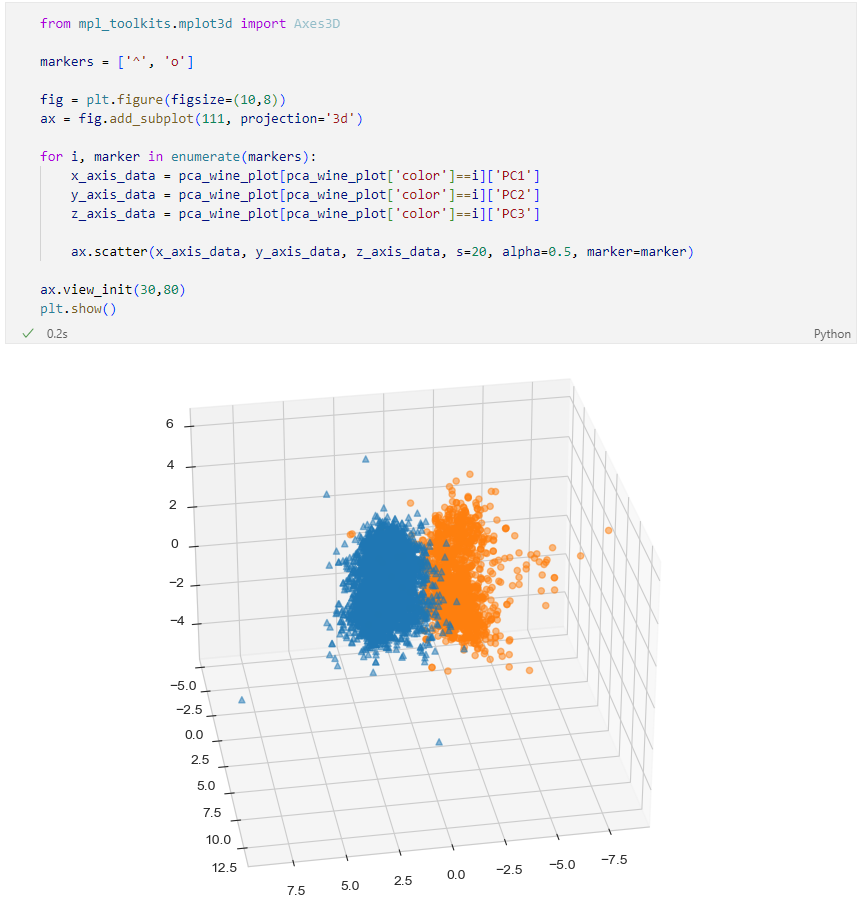
plotly를 이용한 3D 시각화