t-검정 정리

JERRY·2025년 8월 13일

Statistics

목록 보기
12/19

가설검정(Hypothesis Testing)

1. 가설검정이란?

표본 데이터를 이용해 모집단의 특성(모수)에 대한 가설을 세우고, 그 가설이 맞는지 통계적으로 판단하는 절차.

  • 목적: 우연에 의한 결과인지, 아니면 실제로 차이가 있는지를 판단
  • 활용 예시:
    • 신약이 기존 약보다 효과가 있는지 비교
    • 남녀 평균 키의 차이 검정
    • 마케팅 캠페인 전·후 구매율 변화 검정

2. 기본 용어

용어의미
귀무가설 H0H_0차이(효과)가 없다는 주장
대립가설 H1H_1차이(효과)가 있다는 주장
유의수준 α\alpha귀무가설이 맞는데 기각할 확률 (보통 0.05)
검정통계량표본으로 계산한 통계값 (t, z, F, χ² 등)
p-value귀무가설이 참일 때, 현재 데이터보다 극단적인 결과가 나올 확률

3. 가설검정 절차

1. 가설 설정

  • H0H_0 : 두 집단 평균은 같다.
  • H1H_1 : 두 집단 평균은 다르다.

2. 유의수준(α\alpha) 설정

  • ex : α=0.05\alpha = 0.05

3. 데이터 수집 & 검정통계량 계산

  • t-검정, z-검정 등

4. p-value 계산

5. 판단

  • p-value < α → 귀무가설 기각 → 차이가 있음
    p-value ≥ α → 귀무가설 채택 → 차이가 없음

4. 양측검정 vs 단측검정

구분설명예시
양측검정양방향으로 차이를 검정남녀 평균 키가 다른지
단측검정한쪽 방향만 검정남자 평균 키가 여자보다 큰지

5. 오차의 유형

오차 유형의미
제1종 오류 (Type I Error)실제로는 H0H_0이 참인데 기각 → false positive
제2종 오류 (Type II Error)실제로는 H1H_1이 참인데 H0H_0 채택 → false negative

6. 정규성 & 등분산성 검정

가설검정을 수행하기 전, 데이터가 다음 조건을 만족하는지 확인해야 함.

1. 정규성 검정

  • 목적: 데이터가 정규분포를 따른다고 볼 수 있는지 확인
  • 방법:
    • Shapiro-Wilk 검정 (n ≤ 2000)
    • Kolmogorov-Smirnov 검정
    • 시각화: 히스토그램, Q-Q Plot
  • 귀무가설: "데이터는 정규분포를 따른다"
    → p-value < 0.05면 정규분포 아님 → 비모수검정 고려

2. 등분산성 검정

  • 목적: 두 집단 이상이 같은 분산을 가진다고 볼 수 있는지 확인
  • 방법:
    • Levene 검정
    • Bartlett 검정 (정규성 만족 시)
  • 귀무가설: "집단 간 분산은 동일하다"
    → p-value < 0.05면 등분산성 위배

7. 주요 검정 방법

상황검정 방법가정
모집단 σ 알 때, n≥30Z-검정정규성 가정 완화 가능
모집단 σ 모를 때, 두 집단 비교t-검정정규성, 등분산성(스튜던트 t)
등분산성 위배 시Welch t-검정정규성
3개 이상 평균 비교ANOVA정규성, 등분산성
범주형 vs 범주형카이제곱 검정기대도수 ≥ 5
정규성 위배, 2집단Mann–Whitney U 검정비모수
정규성 위배, 3집단 이상Kruskal–Wallis 검정비모수

8. p-value 해석 주의사항

  • p-value는 귀무가설이 참일 확률이 아니다.
  • p-value는 데이터가 귀무가설 하에서 얼마나 극단적인지를 나타낸다.
  • p-value가 작을수록 귀무가설이 맞기 어려움.

1. t-검정이란?

t-검정은 표본에서 추정한 평균이 가설(모집단 평균, 두 집단 평균 차이 등)과 유의하게 다른지를 검정하는 통계 방법입니다.
모집단 분산을 모르는 상황에서 표본분산으로 추정하기 때문에 정규분포 대신 t-분포를 사용합니다.

2. t-검정의 종류

종류목적예시
단일표본 t-검정표본 평균이 특정 값 μ₀와 다른지 검정"우리 고객 평균 월요금이 70달러와 다른가?"
독립표본 t-검정두 집단 평균 비교 (서로 독립)"Churn=Yes vs No의 월요금 차이가 있는가?"
대응표본 t-검정같은 집단의 전·후 비교"프로모션 전후 고객 요금 변화가 있는가?"

Tip: 독립표본에서는 Welch t-test(등분산 미가정)를 기본으로 쓰는 것이 안전합니다.

3. 가정 (Assumptions)

(1) 정규성(Normality) 가정

t-검정의 기본 가정 중 하나는 표본(또는 표본 차이)가 정규분포를 따른다는 것입니다.

  • 이유: t-분포는 정규분포를 기반으로 유도되었기 때문에, 데이터가 크게 벗어나면 검정 결과의 신뢰성이 떨어질 수 있습니다.
  • 예외: 표본 수가 충분히 크면(일반적으로 n ≥ 30) 중심극한정리에 의해 평균이 정규분포에 가까워지므로, 정규성 위배에도 t-검정은 비교적 안정적으로 작동합니다.

정규성 확인 방법

  1. 시각적 방법
    • 히스토그램: 데이터가 종 모양인지 확인
    • QQ-Plot: 데이터의 분위수가 이론적 정규분포 분위수와 직선에 가까운지 확인
  2. 통계적 방법
    • Shapiro–Wilk test
      • 귀무가설(H₀): 데이터는 정규분포를 따른다
      • p-value ≥ 0.05 → 정규성 가정을 기각할 증거 없음
    • Kolmogorov–Smirnov test (표본 크기가 클 때 민감)
    • D’Agostino’s K² test

(2) 등분산성(Homoscedasticity) 가정

독립표본 t-검정(특히 Student t-test)에서는 두 집단의 분산이 동일하다는 가정을 합니다.

  • 이유: 전통적인 t-검정 통계량은 두 집단의 분산을 하나로 묶어(pooled variance) 계산하기 때문입니다.
  • 위배 시 문제: 분산이 크게 다르면 표준오차(SE) 추정이 잘못되어 p-value가 왜곡될 수 있습니다.

등분산성 확인 방법

  1. 시각적 방법
    • 두 그룹의 박스플롯에서 분산(상자·수염 길이) 비교
  2. 통계적 방법
    • Levene’s test
      • 귀무가설(H₀): 두 집단의 분산은 같다
      • p-value ≥ 0.05 → 등분산성 가정을 기각할 증거 없음
      • center='median' 옵션 사용 시 이상치에 강건
    • Bartlett’s test (정규성을 만족할 때만 권장)
    • Brown–Forsythe test (중앙값 기준)

(3) 가정 위배 시 대처 방법

  • 정규성 위배
    • 표본이 크면 t-검정 그대로 사용 가능
    • 비모수 검정(Mann–Whitney U, Wilcoxon signed-rank) 사용
    • 데이터 변환(Log 변환, Box–Cox 등)
  • 등분산성 위배
    • Welch t-test 사용(equal_var=False)
    • 비모수 검정 사용

4. 검정통계량 공식

(1) 단일표본 t-검정

t=xˉ−μ0s/n,df=n−1t = \frac{\bar{x} - \mu_0}{s / \sqrt{n}}, \quad df = n-1

(2) 독립표본 t-검정 (Welch)

t=xˉ1−xˉ2s12n1+s22n2,t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}},
df≈(s12n1+s22n2)2(s12n1)2n1−1+(s22n2)2n2−1df \approx \frac{\left( \frac{s_1^2}{n_1} + \frac{s_2^2}{n_2} \right)^2}{\frac{\left( \frac{s_1^2}{n_1} \right)^2}{n_1 - 1} + \frac{\left( \frac{s_2^2}{n_2} \right)^2}{n_2 - 1}}

(3) 대응표본 t-검정

t=dˉsd/n,df=n−1t = \frac{\bar{d}}{s_d / \sqrt{n}}, \quad df = n-1

5. 가설 설정

  • 양측 검정: 평균이 서로 다른지(≠)
  • 단측 검정: 한쪽 방향으로만 차이가 있는지(>, <)
  • 방향은 사전에 설정해야 합니다.

6. 신뢰구간 (Confidence Interval)

  • 평균 차이의 95% CI:
    (xˉ1−xˉ2)±tα/2,df⋅SE(\bar{x}_1 - \bar{x}_2) \pm t_{\alpha/2, df} \cdot SE
  • CI가 0을 포함하지 않으면 평균 차이는 통계적으로 유의합니다.

7. 효과크기 (Effect Size)

  • Cohen’s d:
    d=xˉ1−xˉ2spd = \frac{\bar{x}_1 - \bar{x}_2}{s_p}
    • 0.2 = 작음, 0.5 = 중간, 0.8 = 큼
  • Hedges’ g: 작은 표본 보정이 적용된 Cohen’s d

8. 점검 체크리스트

  • 정규성: QQ-plot, Shapiro-Wilk (소표본)
  • 등분산성: Levene test (center='median' 권장)
  • 이상치: 박스플롯, IQR
  • 다중비교 시 보정: Bonferroni, Holm
  • 효과크기와 신뢰구간 함께 보고

9. Telco 데이터 예제 (Welch t-test + 전제 조사 + 시각화)

import kagglehub
import os
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from scipy import stats

# 데이터 로드
path = kagglehub.dataset_download("blastchar/telco-customer-churn")
churn = pd.read_csv(path + '/' + os.listdir(path)[0])

# 그룹 나누기
yes = churn.loc[churn['Churn']=='Yes', 'MonthlyCharges'].astype(float).dropna()
no = churn.loc[churn['Churn']=='No', 'MonthlyCharges'].astype(float).dropna()
# 1. 정규성 검사 (Shapiro-Wilk)

shapiro_yes = stats.shapiro(yes.sample(500, random_state=42))  # 표본 500개
shapiro_no = stats.shapiro(no.sample(500, random_state=42))

print(f"Shapiro-Wilk (Yes): W={shapiro_yes[0]:.4f}, p={shapiro_yes[1]}")
print(f"Shapiro-Wilk (No) : W={shapiro_no[0]:.4f}, p={shapiro_no[1]}")
Shapiro-Wilk (Yes): W=0.9329, p=3.398378854799905e-14
Shapiro-Wilk (No) : W=0.9116, p=1.756265906105648e-16

Shapiro-Wilk p-value < 0.05 
→ 정규성 가정 위배 가능성 있음
  그러나 표본 수가 크면 작은 왜도/첨도 차이에도 p<0.05가 되므로 QQ-Plot 시각적 확인 병행 필요
  Telco 데이터에서는 약간의 비정규성(꼬리 두꺼움)이 있으나, 표본 크기가 커서 Welch t-test 적용에 큰 문제 없음
# 2. 등분산성 검사 (Levene test)

levene_stat, levene_p = stats.levene(yes, no, center='median')
print(f"Levene test: stat={levene_stat:.4f}, p={levene_p}")
Levene test: stat=361.8445, p=1.0261244899421871e-78

Levene test p-value < 0.05 
→ 등분산성 위배 → Welch t-test 사용이 적절
# 3. Welch t-test

t_stat, p_val = stats.ttest_ind(yes, no, equal_var=False)

# 평균 차이 및 95% CI
mean_diff = yes.mean() - no.mean()
se = np.sqrt(yes.var(ddof=1)/len(yes) + no.var(ddof=1)/len(no))
df = (yes.var(ddof=1)/len(yes) + no.var(ddof=1)/len(no))**2 / (
     (yes.var(ddof=1)/len(yes))**2/(len(yes)-1) + (no.var(ddof=1)/len(no))**2/(len(no)-1))
alpha = 0.05
t_crit = stats.t.ppf(1-alpha/2, df)
ci_low, ci_high = mean_diff - t_crit*se, mean_diff + t_crit*se

print(f"Welch t = {t_stat:.4f}, df ≈ {df:.1f}, p = {p_val:.3e}")
print(f"Mean diff (Yes-No) = {mean_diff:.3f}")
print(f"95% CI = [{ci_low:.3f}, {ci_high:.3f}]")
Welch t = 18.4075, df ≈ 4135.8, p = 8.592e-73
Mean diff (Yes-No) = 13.176
95% CI = [11.773, 14.580]

Welch t = 18.4075 → 평균 차이가 표준오차 대비 매우 큼
df ≈ 4135.8 → Welch–Satterthwaite 근사 자유도, 표본이 크기 때문에 df가 상당히 큼
p = 8.592 × 10⁻⁷³ → 귀무가설(평균 차이 없음)을 기각할 충분한 통계적 증거
Mean diff (Yes–No) = 13.176  → Churn=Yes 고객의 평균 월요금이 No보다 약 13.18달러 높음
95% CI = [11.773, 14.580] → 모평균 차이가 95% 신뢰수준에서 이 범위 안에 있을 것, CI에 0이 포함되지 않으므로 차이는 통계적으로 유의
# 4. 시각화

plt.figure(figsize=(8,5))
sns.boxplot(x='Churn', y='MonthlyCharges', data=churn, palette='Set2')
plt.title('MonthlyCharges by Churn')
plt.show()

# QQ-plot
fig, ax = plt.subplots(1,2, figsize=(8,4))
stats.probplot(yes, dist="norm", plot=ax[0])
ax[0].set_title("QQ-Plot: Churn=Yes")
stats.probplot(no, dist="norm", plot=ax[1])
ax[1].set_title("QQ-Plot: Churn=No")
plt.show()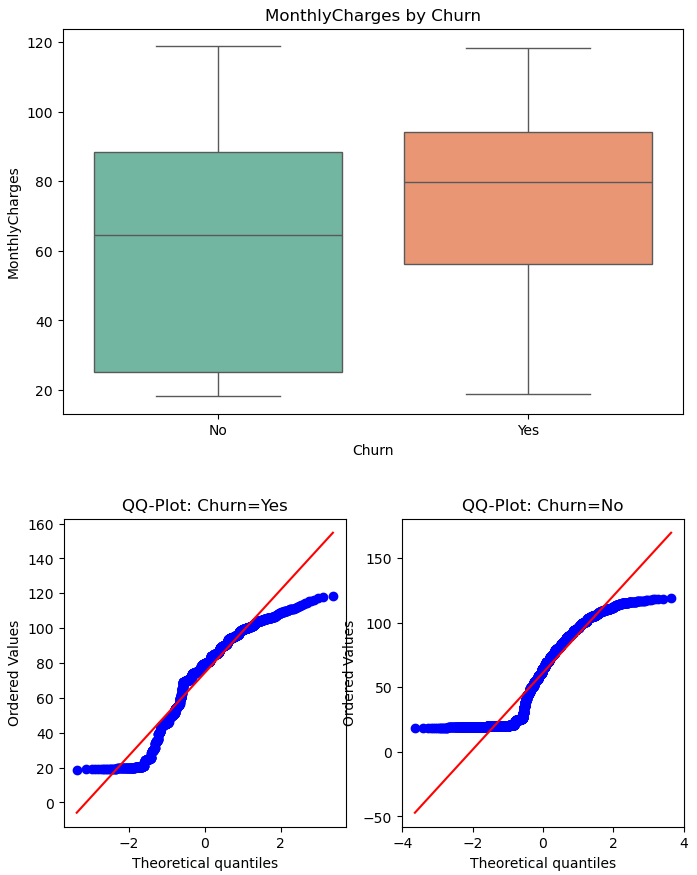
이미지 설명 
(박스플롯)
Churn=Yes의 중앙값이 더 높음
분포가 오른쪽 꼬리를 가짐(고요금 고객 존재)

(QQ-Plot)
양쪽 끝에서 직선에서 벗어나는 모습 → 완벽한 정규성은 아님
하지만 큰 표본에서는 평균 비교 검정에 큰 영향 X

[결론]
정규성: 일부 위배, 하지만 표본이 크므로 t-검정 적용 가능
등분산성: 위배 → Welch t-test 사용
차이 해석: 고요금 고객에서 이탈률이 높을 가능성이 있음 → 가격 정책 검토 필요
profile
JERRY
이전 포스트

Machine Learning 알고리즘과 실제 활용 소개

다음 포스트

비모수 검정

0개의 댓글