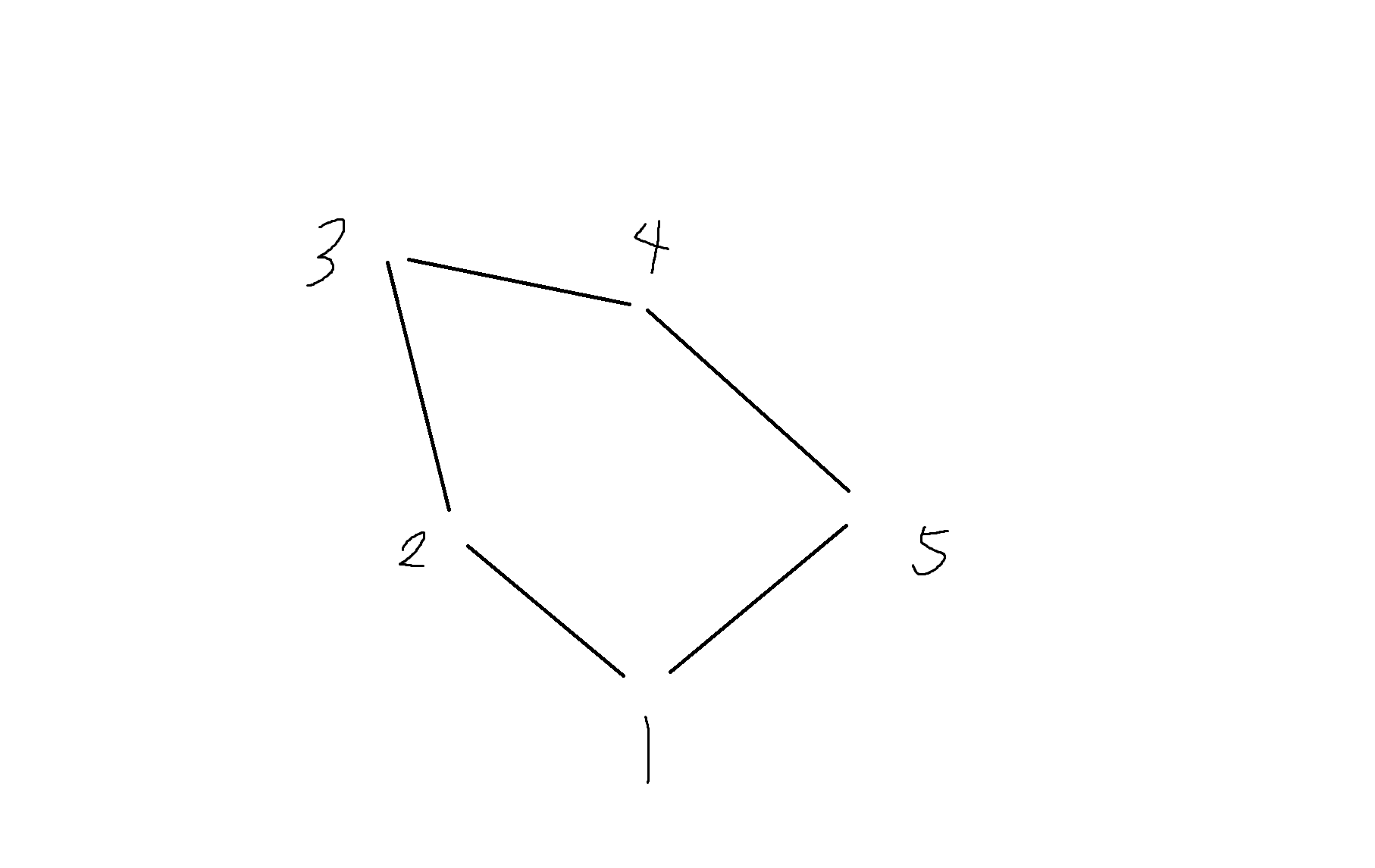
하세도표
- 독일의 수학자 하세가 부분순서 집합 (A, ~<)를 그래프로 나타낼 때 고안하여 사용함
- 방향 그래프의 일종으로서 화살표는 표기하지 않고 모든 연결선(edge)을 트리(tree)와 같이 모두 아래 방향을 향하도록 그림
- 모든 순서(loop)은 표시하지 않고 집합 A의 원소 x,y,z에서 x<=y이고 y<=z를 만족하는 y가 존재하지 않는 경우에는 x에서 z로의 연결을 그려줌. (반대로 두 관계가 만족하는게 있으면 그리지 않는다)
예제 5-24. 다음과 같이 주어진 방향그래프가 부분순서 관계임을 보이고, 그 그래프를 하세도표로 나타내어라.
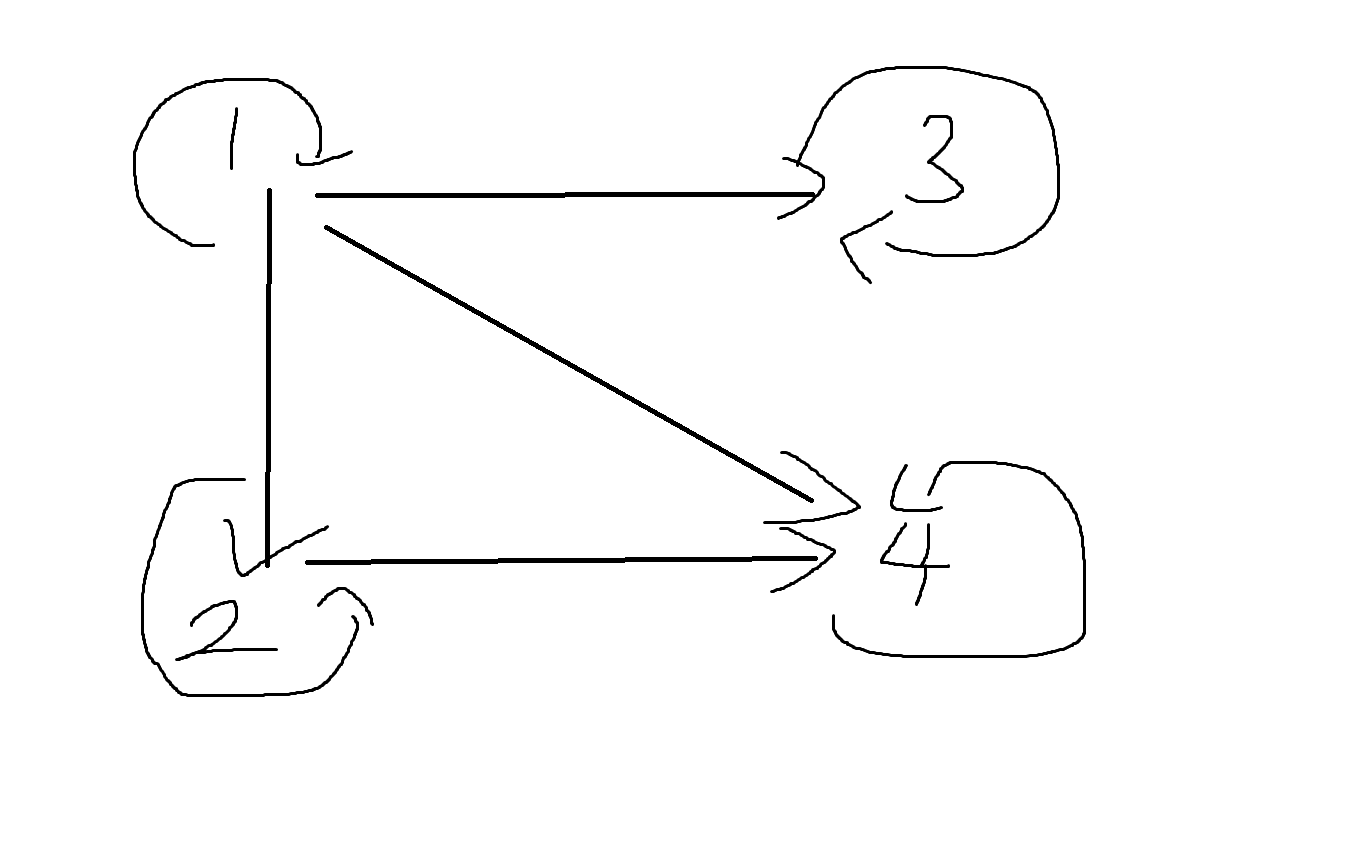
부분순서관계 조건
1) 반사 O
2) 반대칭 O
3) 추이 O
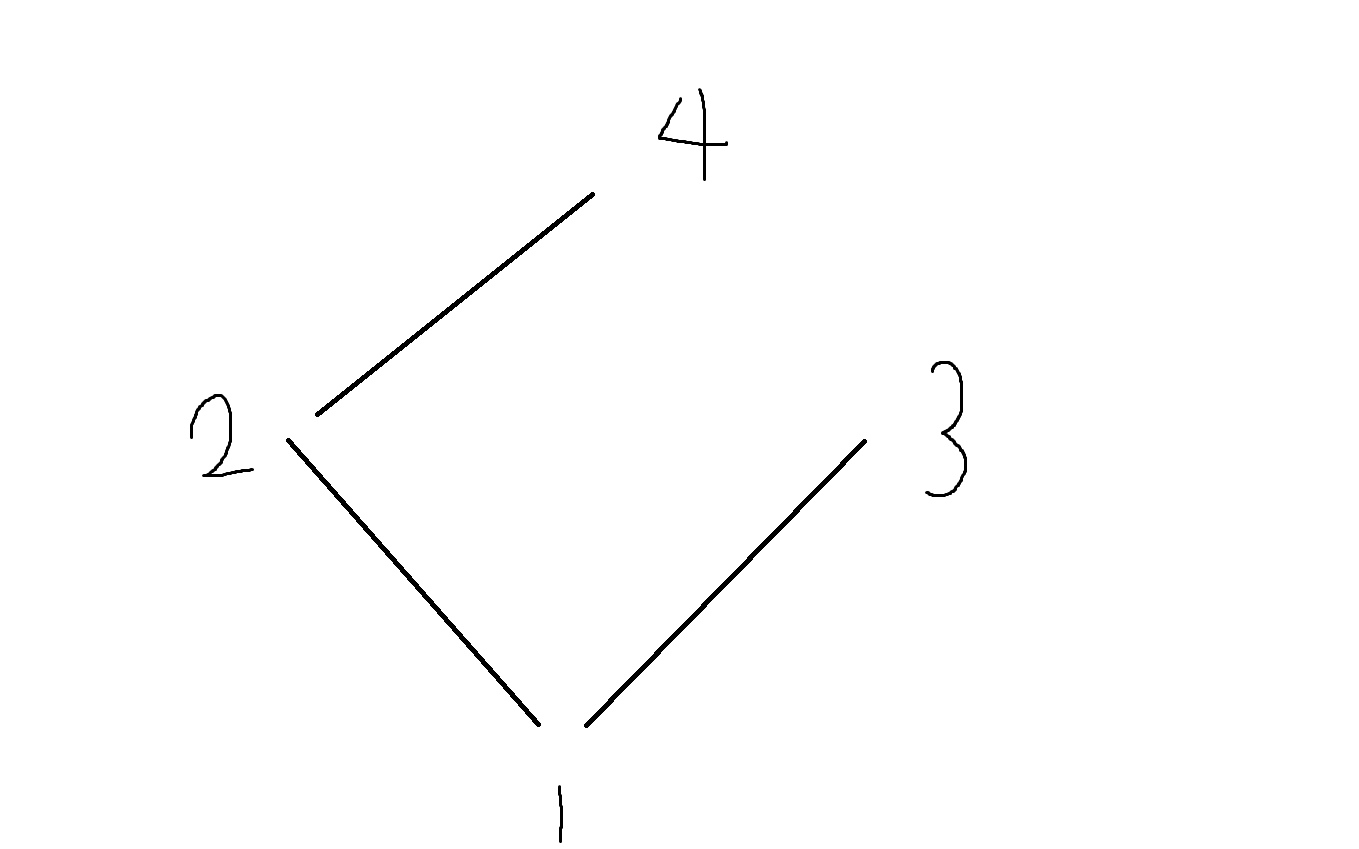
하세도표로 뭘 알수있느냐
-> 1이 2,3보다 앞에 있다
-> 2가 4보다 앞에 있다.
(1-2-4가 있으므로 1->4는 연결하지 않는다.)
비교가능
- 부분순서집합 (A, ~<)에서 집합 A의 두 원소 x,y가 x~<y 또는 y~<x이면 x와 y는 비교가능이라고 한다.
선형순서집합
- 집합 A의 모든 두 원소가 비교가능하면 A를 선형순서집합이라 한다
선행순서관계
- 선형순서집합인 경우 관계 ~<라고 함
정의 5-15
집합 A에서의 관계 R이 다음 조건을 만족할 경우 선형순서라고 한다.
(1) R이 부분순서를 만족한다.
(2) 만약 a∈A, b∈A라면 aRb, bRa 또는 a=b 중 하나가 성립한다.
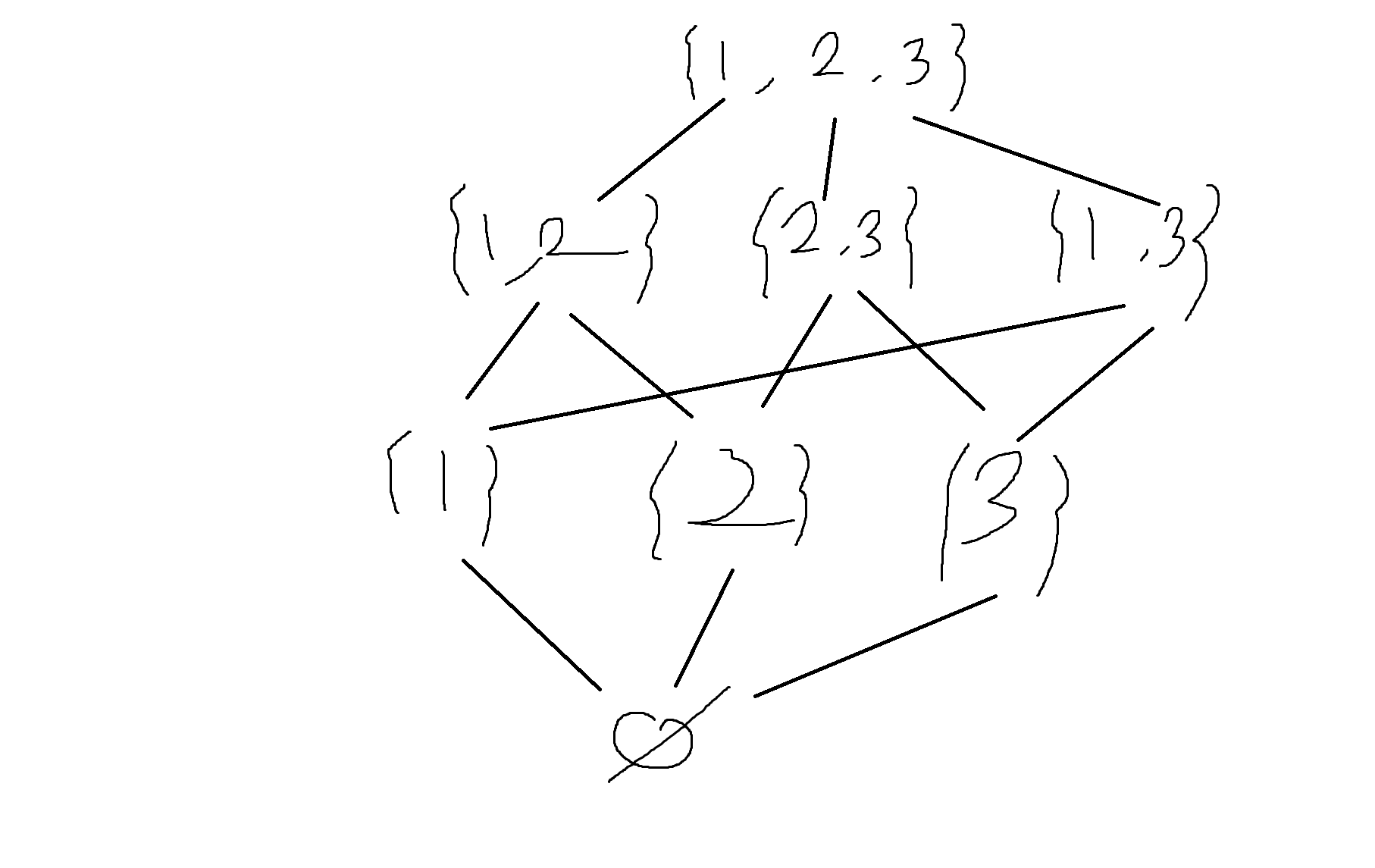
예제 5-35. 집합 A = {1,2,3}의 부분집합들에 대한 포함관계를 하세도표로 작성해보라
∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3} ,{1,2,3}
연습문제
1) S = {1,2,3,4,5,6}의 부분집합이 다음과 같을 때 집합 S를 분할하는지 판단하시오.
{{1,2}, {3,4}, {5}}
1) ∅ 아님 O
2) 교집합 없음 O
3) 다 합해서 전체? -> X
-> 분할 X
2) 정수의 집합 Z에 대한 관계 ≡이 Z에 있는 두 원소 x,y에 대하여 x-y가 성립할 때, 관계 ≡이 동치 관계인지를 밝히시오
- 반사 O (x-y 정수 -> 반사 성립)
- 대칭 O (x-y 정수 -> y-x도 정수)
- 추이 O (x-y가 정수 -> y-z가 정수 -> x-z도 정수) -> O
따라서 동치관계가 맞다.
3) 관계 R이 다음과 같을 때, R이 부분순서관계 임을 보이고 하세도표를 그리시오.
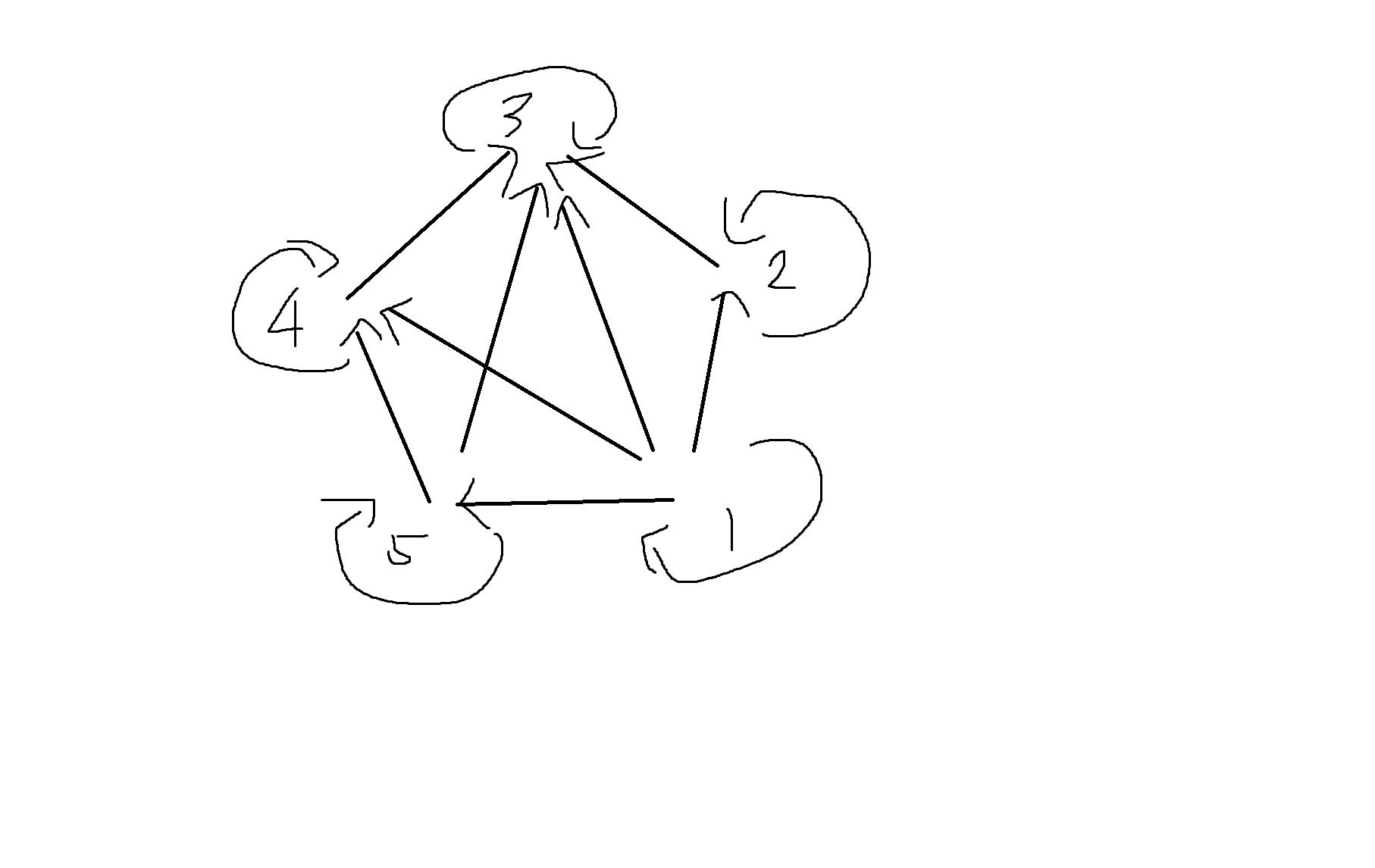
부분순서관계
1) 반사 O
2) 반대칭 O
3) 추이 O
-> 부분순서관계 성립 O
하세도표