함수 - 관계의 특수한 형태로서 첫번째 원소가 같지 않은 순서쌍들의 집합
R = {(a,b), (c,d)... (a,d)} -> 이러면 안된다는 것
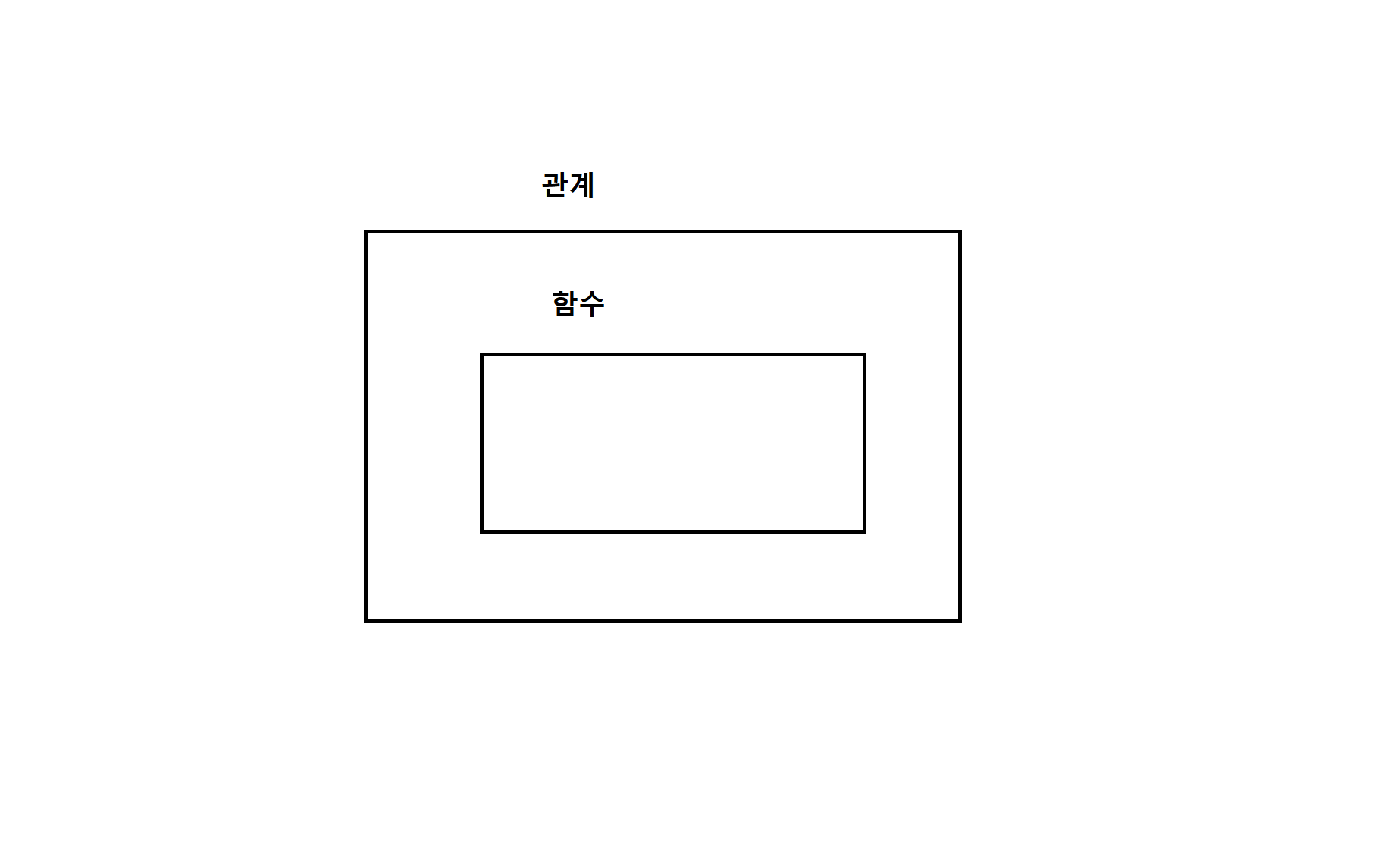
- 한 집합의 원소들과 다른 집합의 원소들간의 관계를 나타내는 순서쌍 중에서 앞에 있는 집합의 모든 원소가 한번씩만 순서쌍에 포함될 경우
- 여러가지 수학의 도구 중 가장 중요한 개념의 하나
정의 6-1. 두 집합 X와 Y에서 함수 f는 집합 X에서 Y로의 관계의 부분집합으로서, 집합 X에 있는 모든 원소 x가 집합 y에 있는 원소 중 오직 하나에만 대응되는 관계를 말한다.
f: X->Y
X를 f의 정의역, Y를 f의 공변역이라 한다.
함수 f의 정의역(domain)은 Dom(f)라 표시
함수 f의 치역(range)은 Ran(F)라 표시 (공변역 != 치역)
예제 6-3) A를 인터넷 온라인상의 사진 동호회 회원들의 집합이라고 할때, 다음의 대응이 A에 관한 함수가 되는지 알아보자.
(1) 각 회원에 그 사람의 나이를 대응 -> O
(2) 각 회원에 그 사람의 성별을 대응 -> O
(3) 각 회원에 그 사람의 배우자를 대응 -> X (결혼안한 사람 존재)
예제 6-4) 다음의 관계가 함수인지 여부, 만약 함수면 정의역, 공변역, 치역을 각각 구해라.
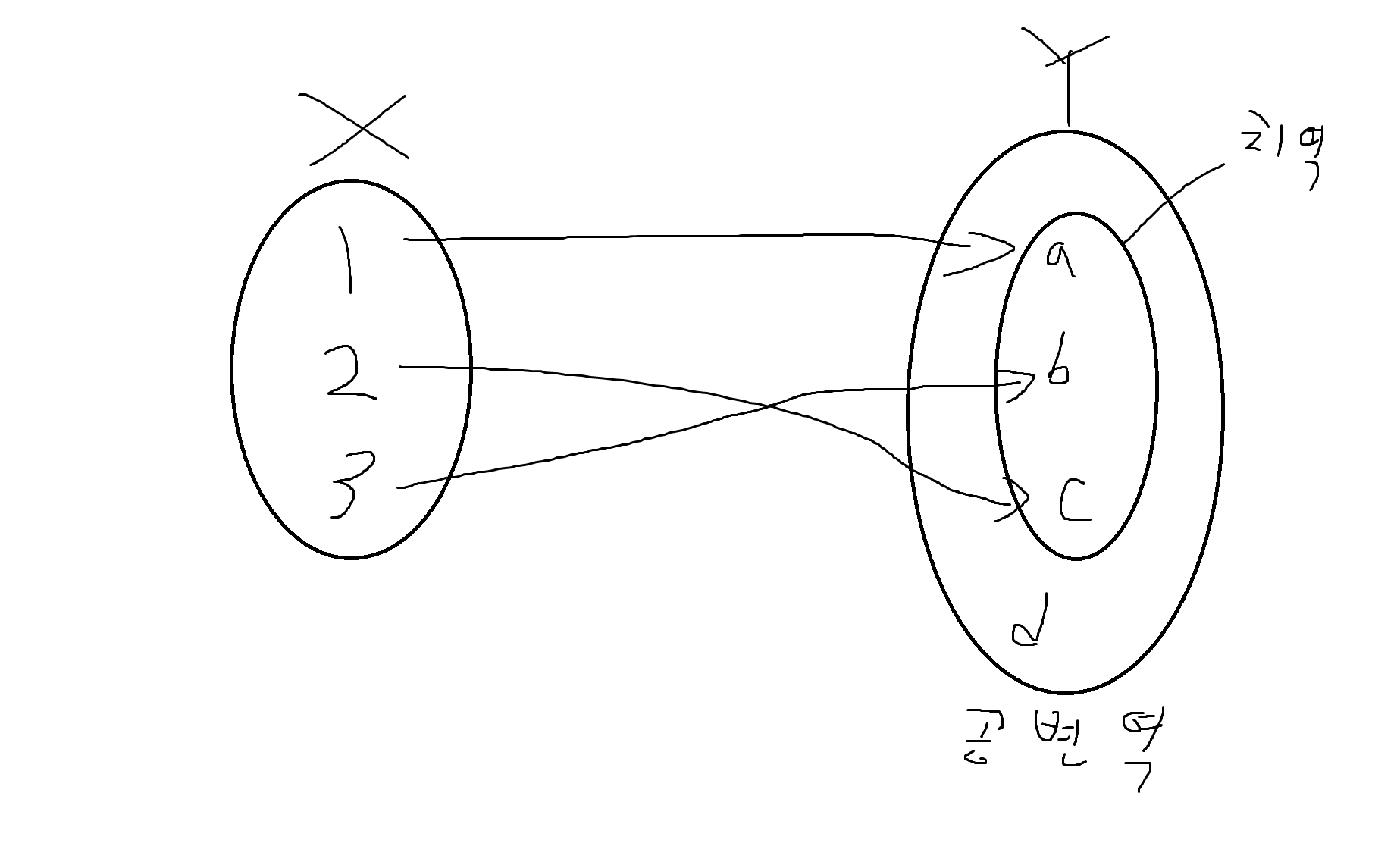
(1) {(1,a), (1,b), (2,c), (3,b)} -> X (b에 두개 묶임)
(2) {(a,a}, (b,b), (c,c)} -> O
(3) {(x,y)| x,y ∈ Z, y-x = 1} -> O (y=x+1)
(4) {(x,y)| x,y ∈ N, y-x = 1} -> 정의역은 자연수, 치역은 2보다 큰 자연수
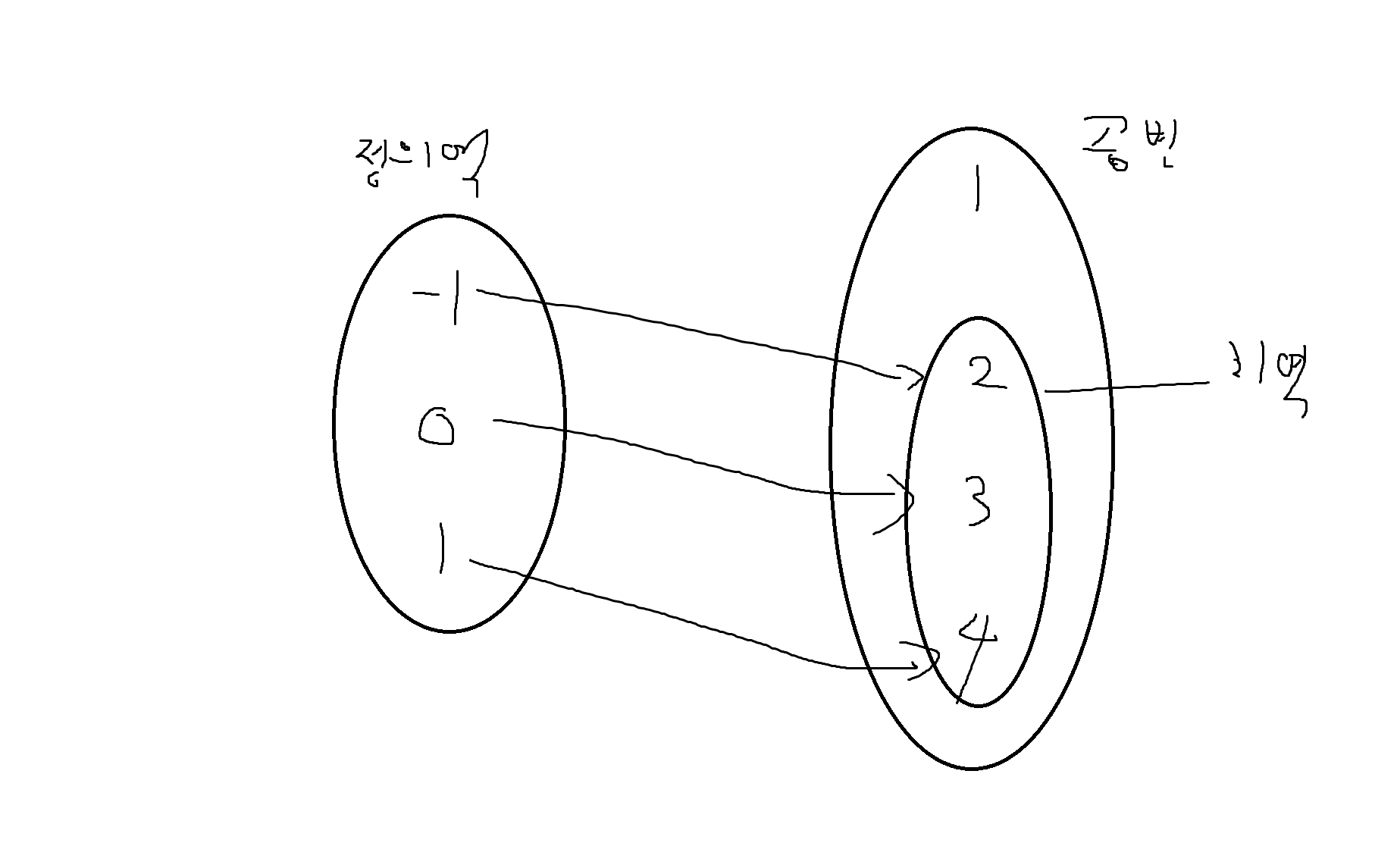
예제 6-5) A = {-1,0,1}, B = {1,2,3,4}에 대한 관계가 {(x,y)|x∈A, y∈B, y=x+3} 일 때 이 관계가 함수인지 판별, A의 원소값에 대한 함수값을 구해라.
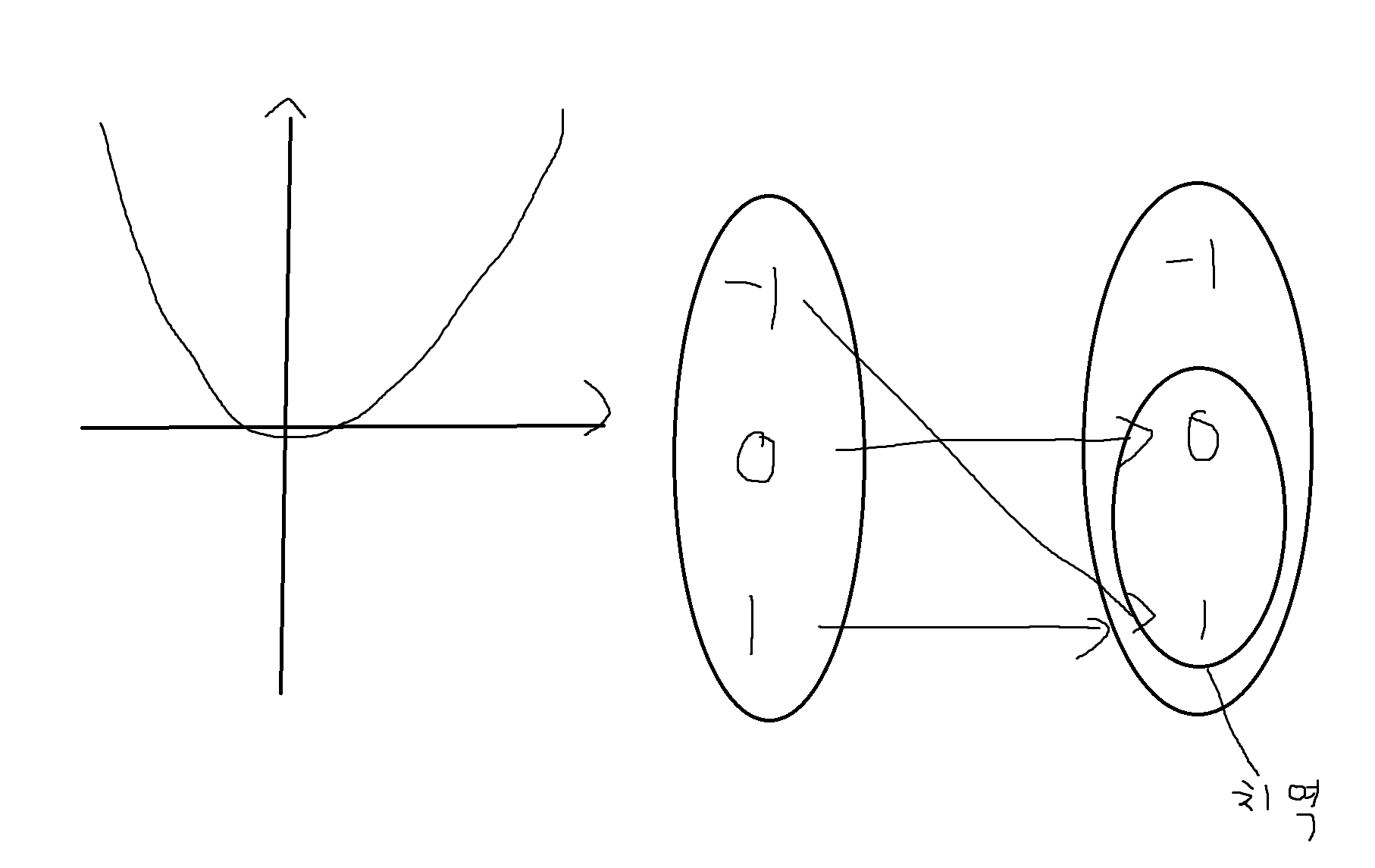
예제 6-6) A = {-1, 0, 1}에서 f:A->A가 f(x) = x²으로 주어졌을때 함수가 되는지를 판별하고, 정의역과 치역 그리고 공변역을 구해보자.
-> 정의역이 한번씩만 쓰이므로 함수가 맞다.
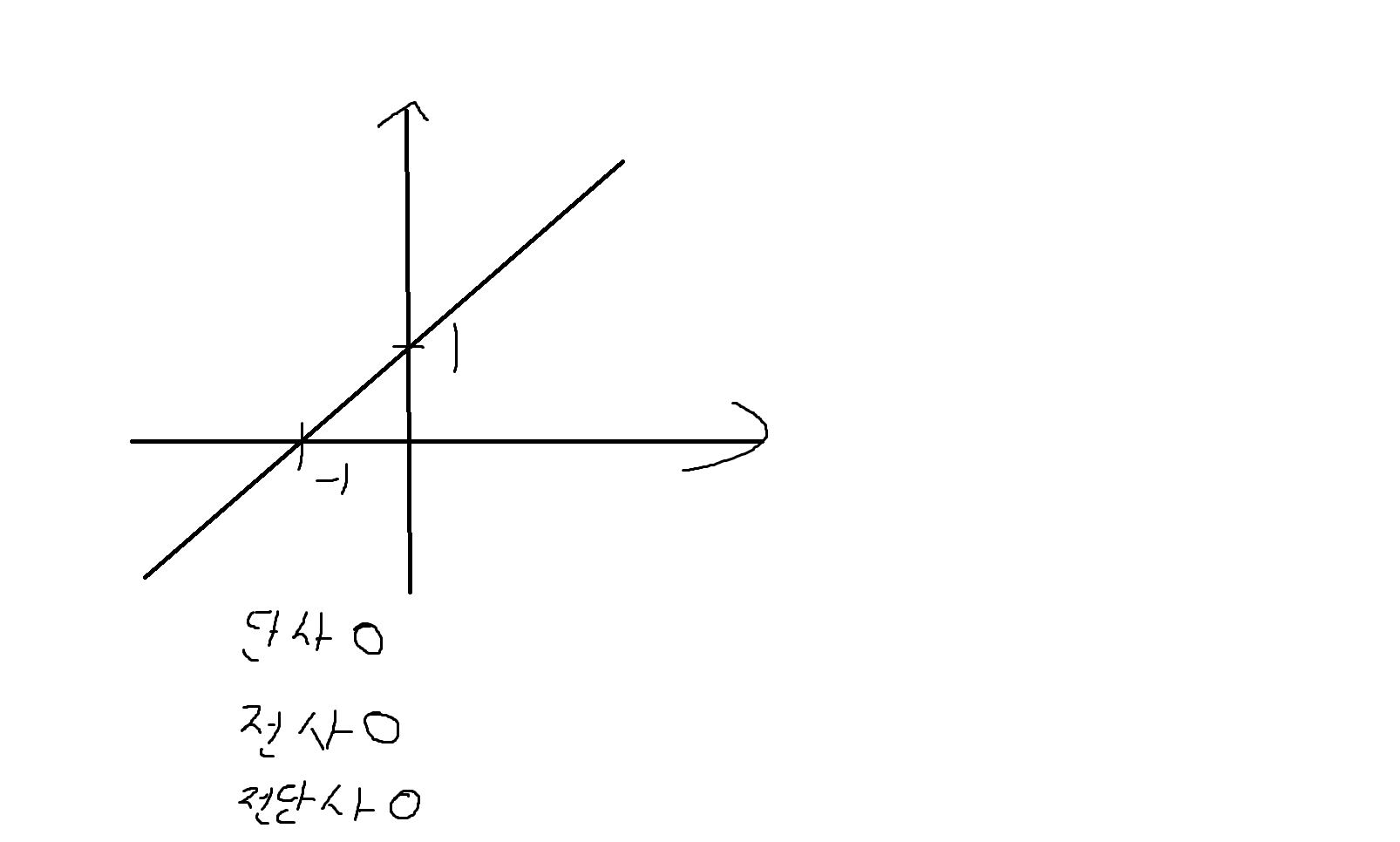
예제 6-7) 함수 f:R->R일때 다음과 같은 함수 그래프를 순서쌍의 집합으로 표시하고, 좌표평면상에 나타내보자.
(1) y = x+2
| X | Y |
|---|---|
| -2 | 0 |
| -1 | 1 |
| 0 | 2 |
| 1 | 3 |
| 2 | 4 |
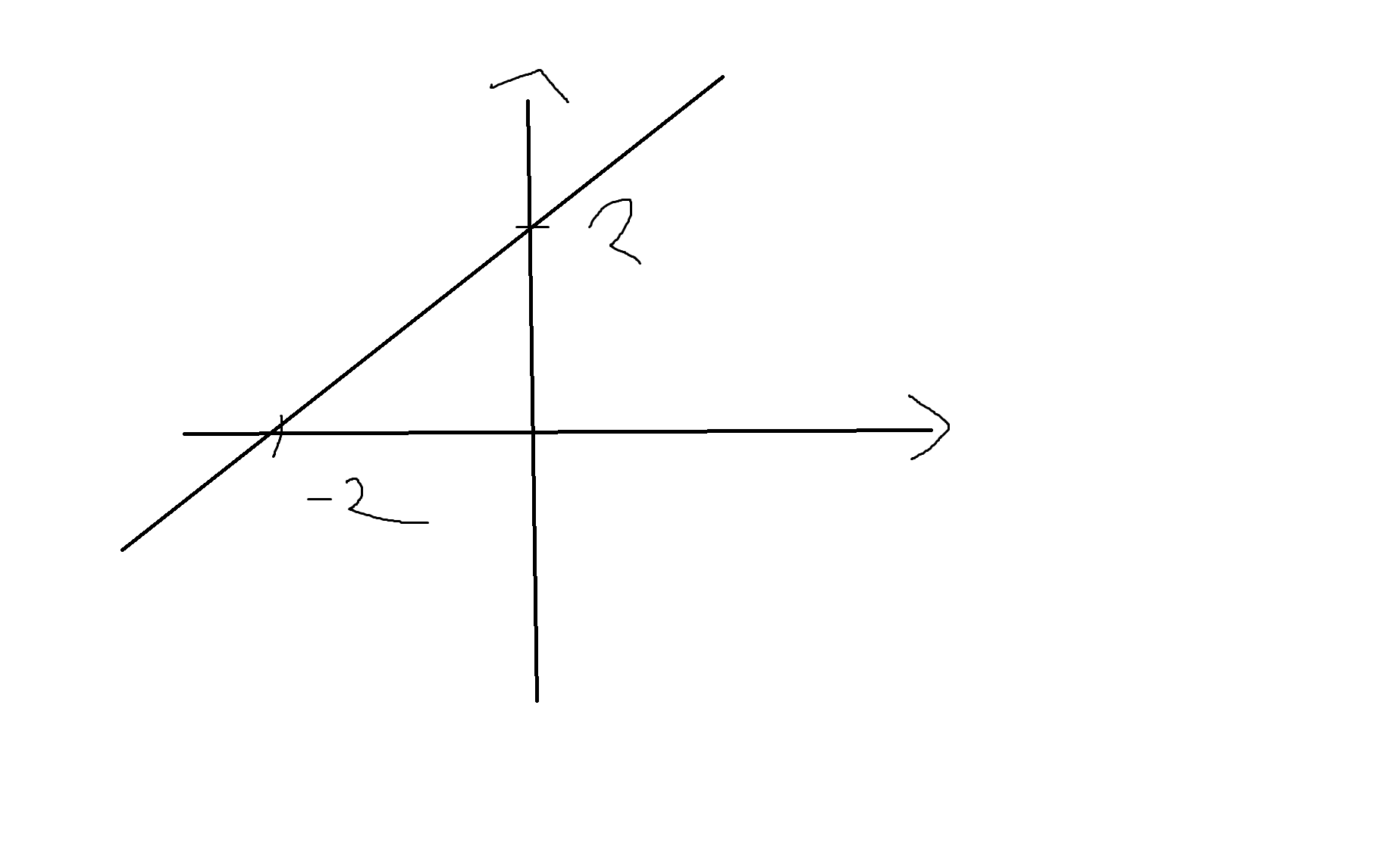
(2) y = x²
| X | Y |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
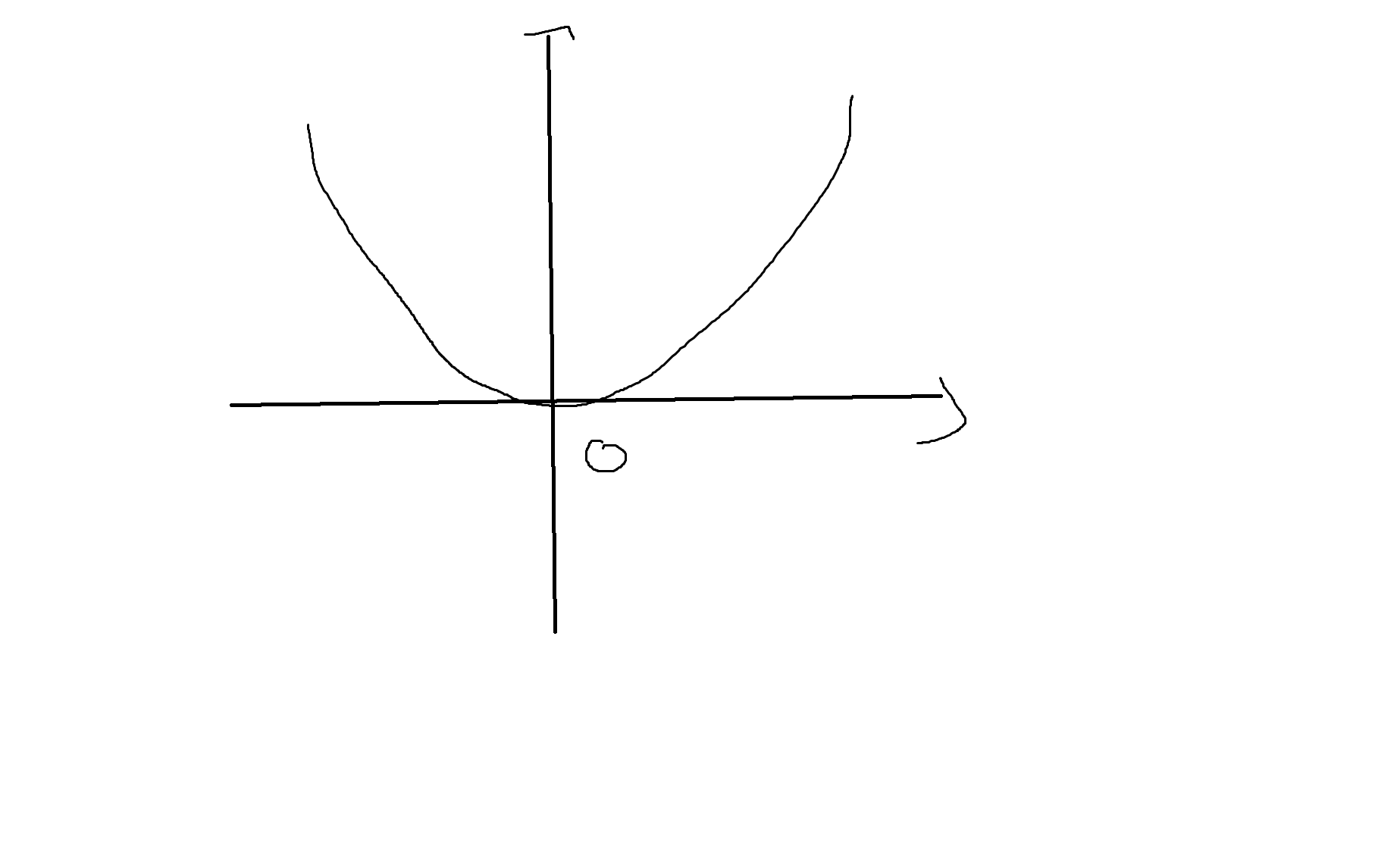
(3) y = |x|
| X | Y |
|---|---|
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
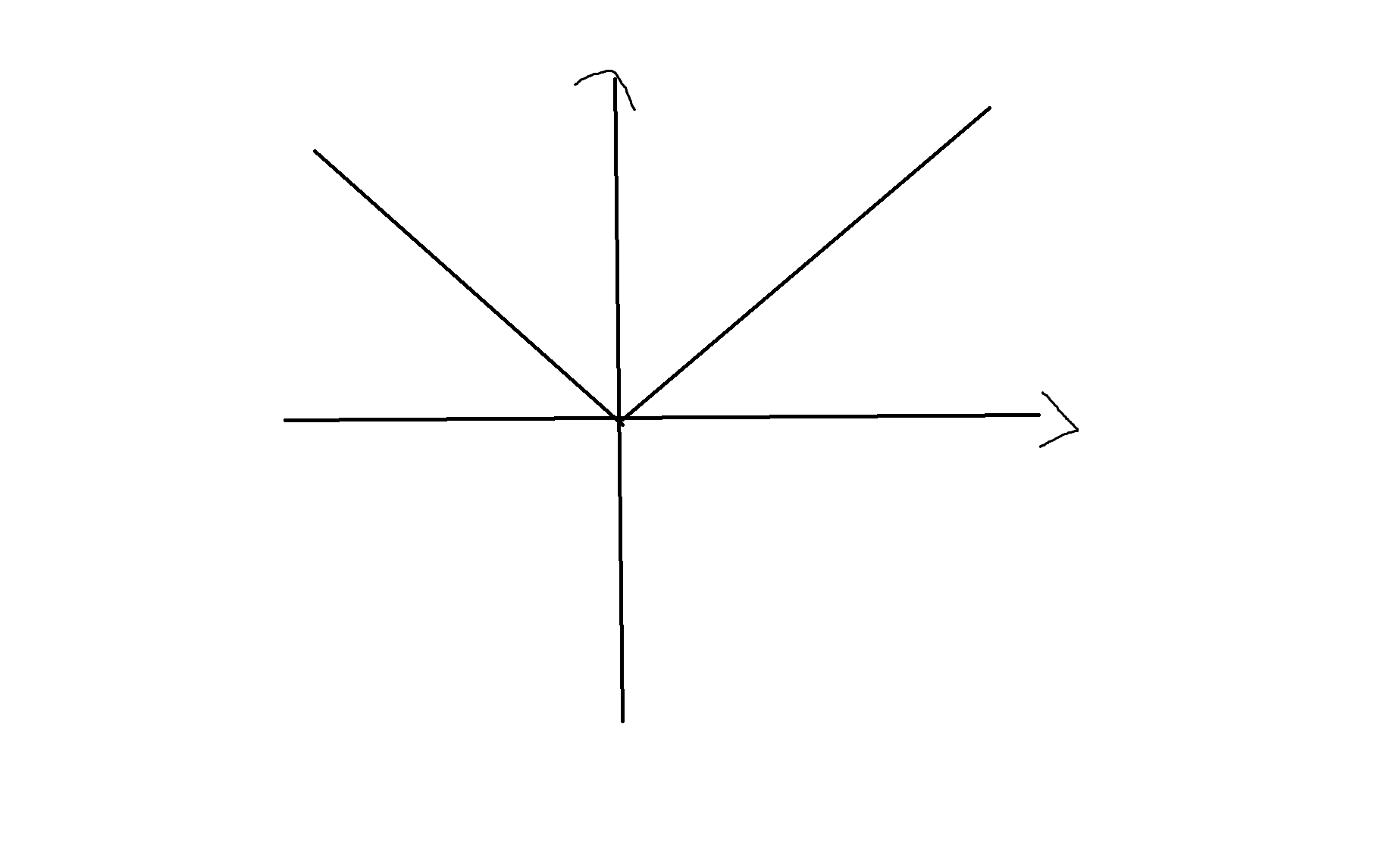
(4) y = 2^x (지수)
| X | Y |
|---|---|
| -2 | 1/4 |
| -1 | 1/2 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
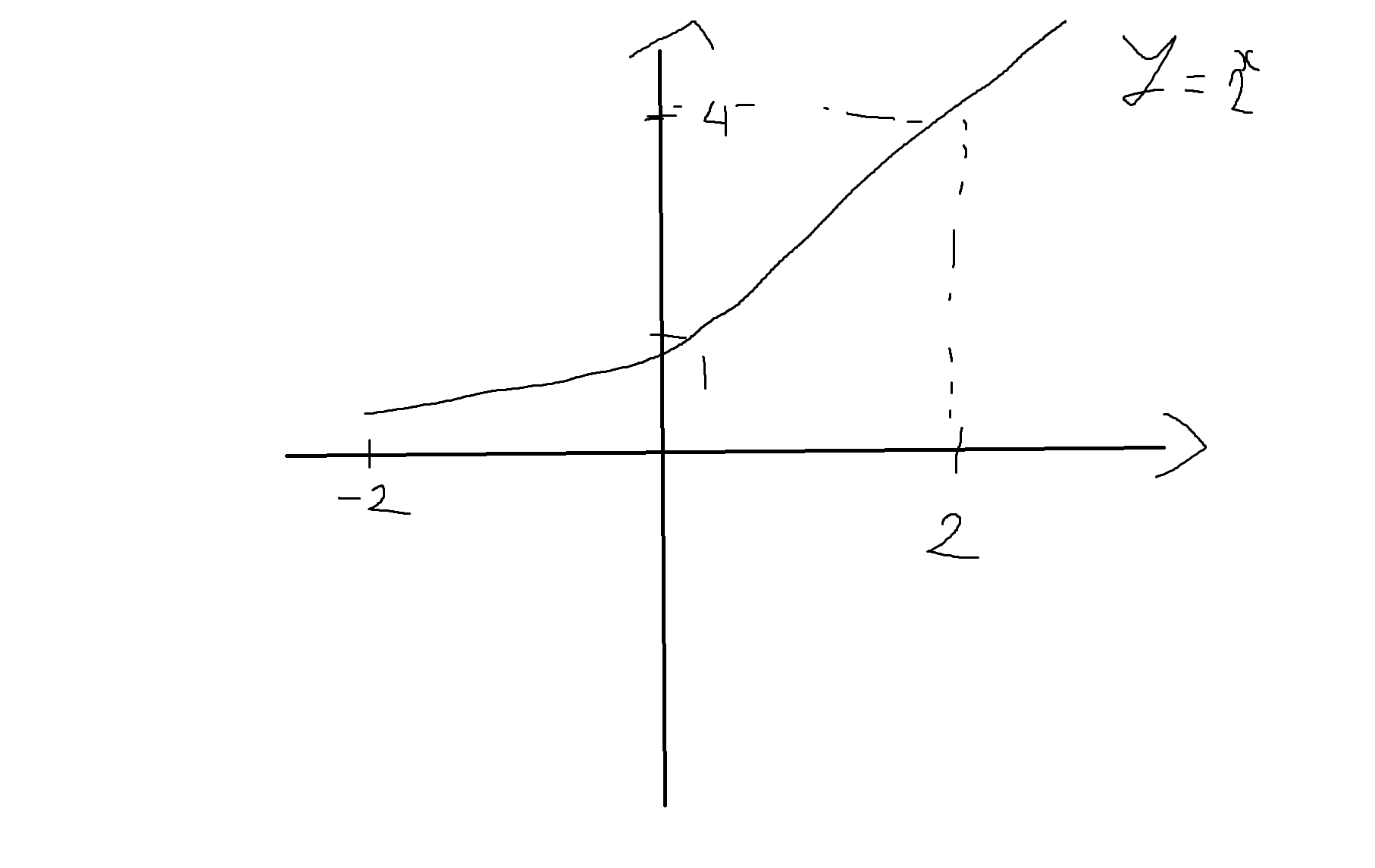
단사함수, 전사함수, 전단사함수
정의 6-3. 함수 f:A->B에서 ai, aj ∈ A에 대하여 f(ai) = f(aj) 이면 ai=aj일 경우, 함수 f를 단사함수라고 한다. 즉,
∀ai, aj ∈ A, f(ai) = f(aj) => ai = aj
단사함수 -> x가 다르면 다른 값을 가리켜야 함 (일대일 함수)
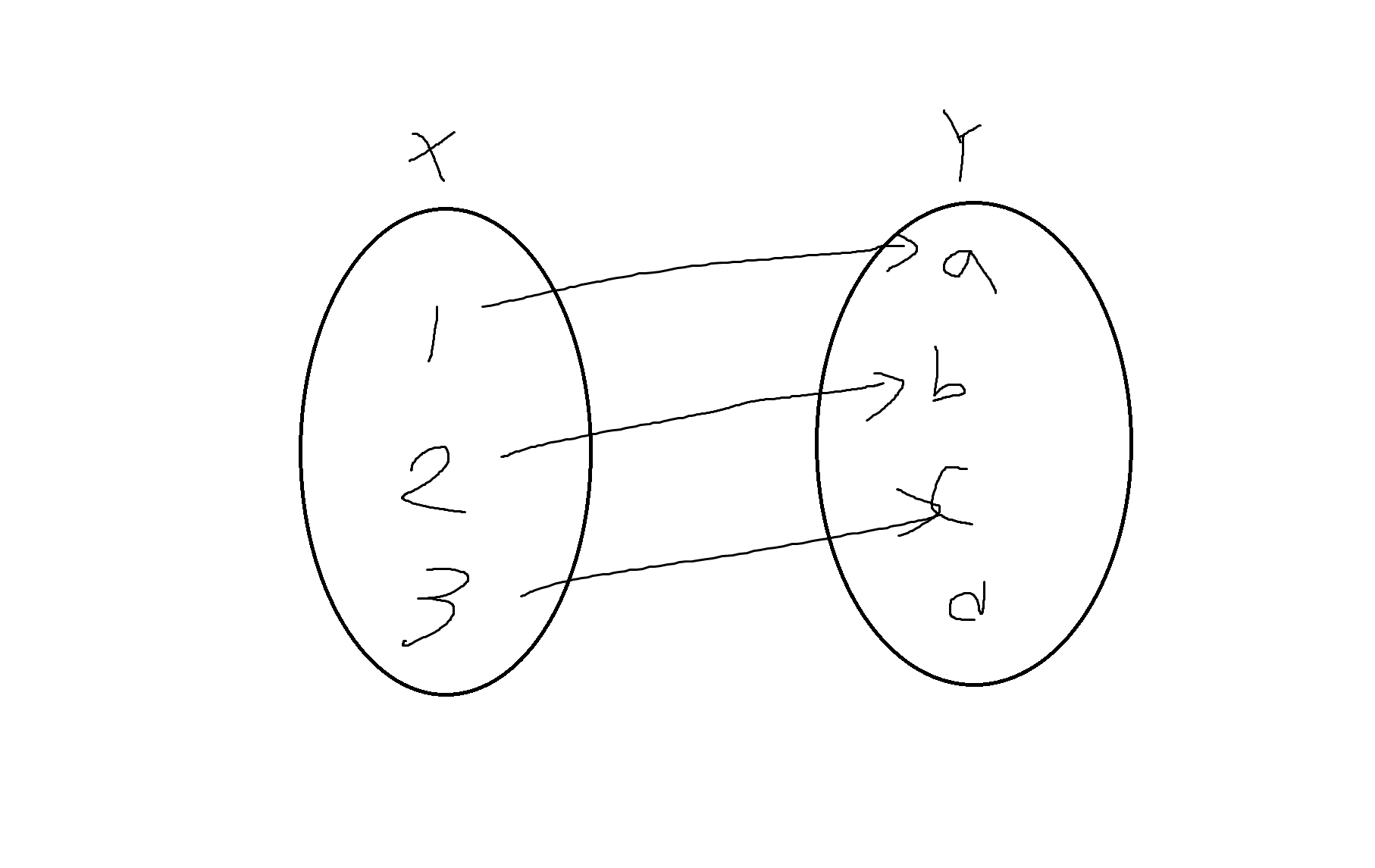
정의 6-4. 함수 f:A->B에서 B의 모든 원소 b에 대하여 f(a) = b가 성립하는 a∈A가 적어도 하나 존재할때, 전사함수라 한다. 즉,
∀b ∈ B, ∃a ∈ A, f(a) = b
(공변역과 치역이 같다) (반영함수)
a->1
b->2
c->3
4(x)
정의 6-5. 함수 f: A->B에서 f가 단사함수인 동시에 전사함수일때, 함수 f를 전단사 함수라 한다. (일대일 대응함수)
(일대일대응 + 공변=치역)
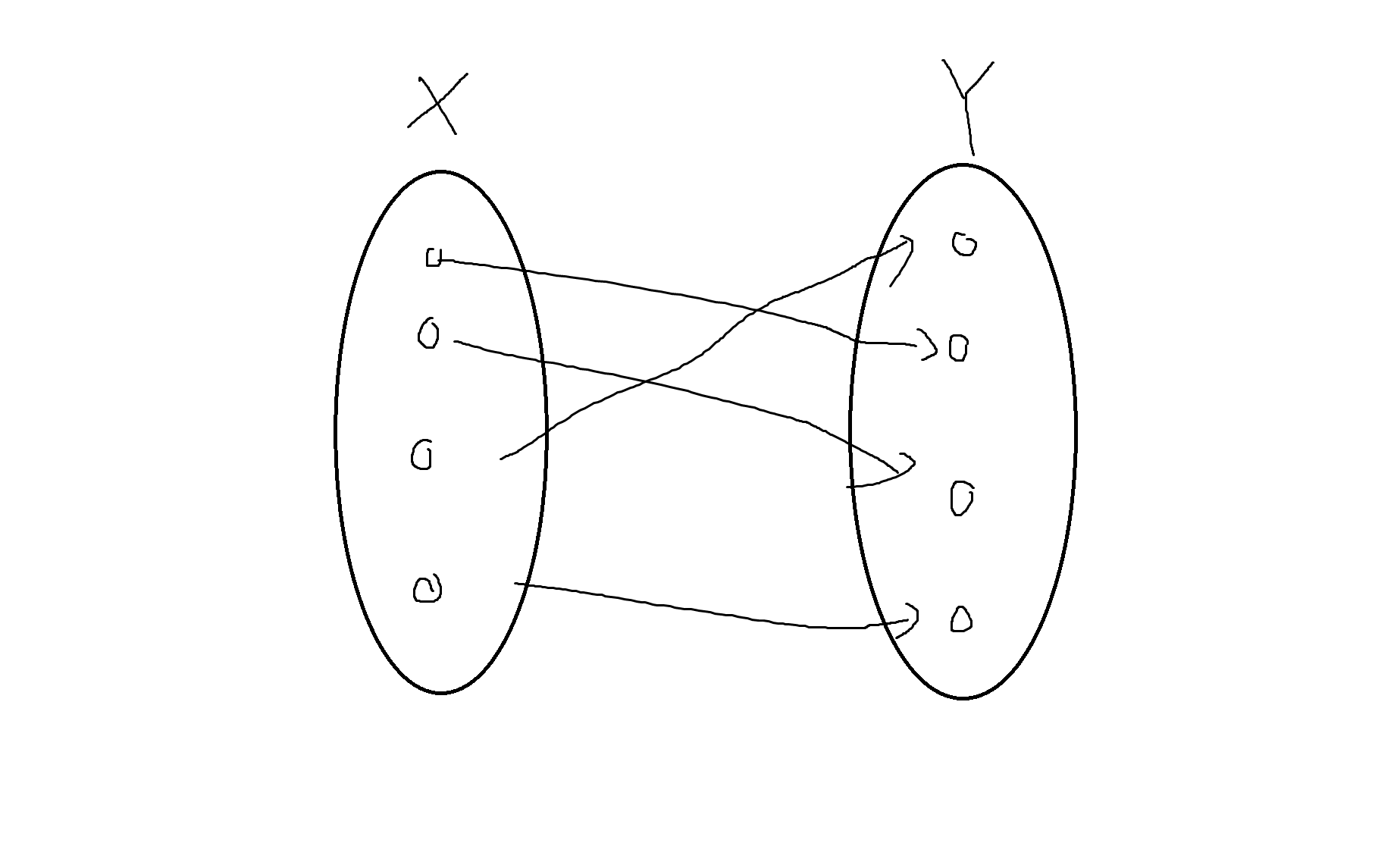
함수 f:A->B에서 함수 f의 특성
1) f가 단사함수인 경우에 B의 모든 원소가 A의 원소와 반드시 대응하는 것은 아니므로 A의 원소와 B의 원소의 개수를 비교하면 |A| <= |B|이 성립됨.
즉, B의 원소의 개수는 A의 원소의 개수보다 크거나 같아야됨.
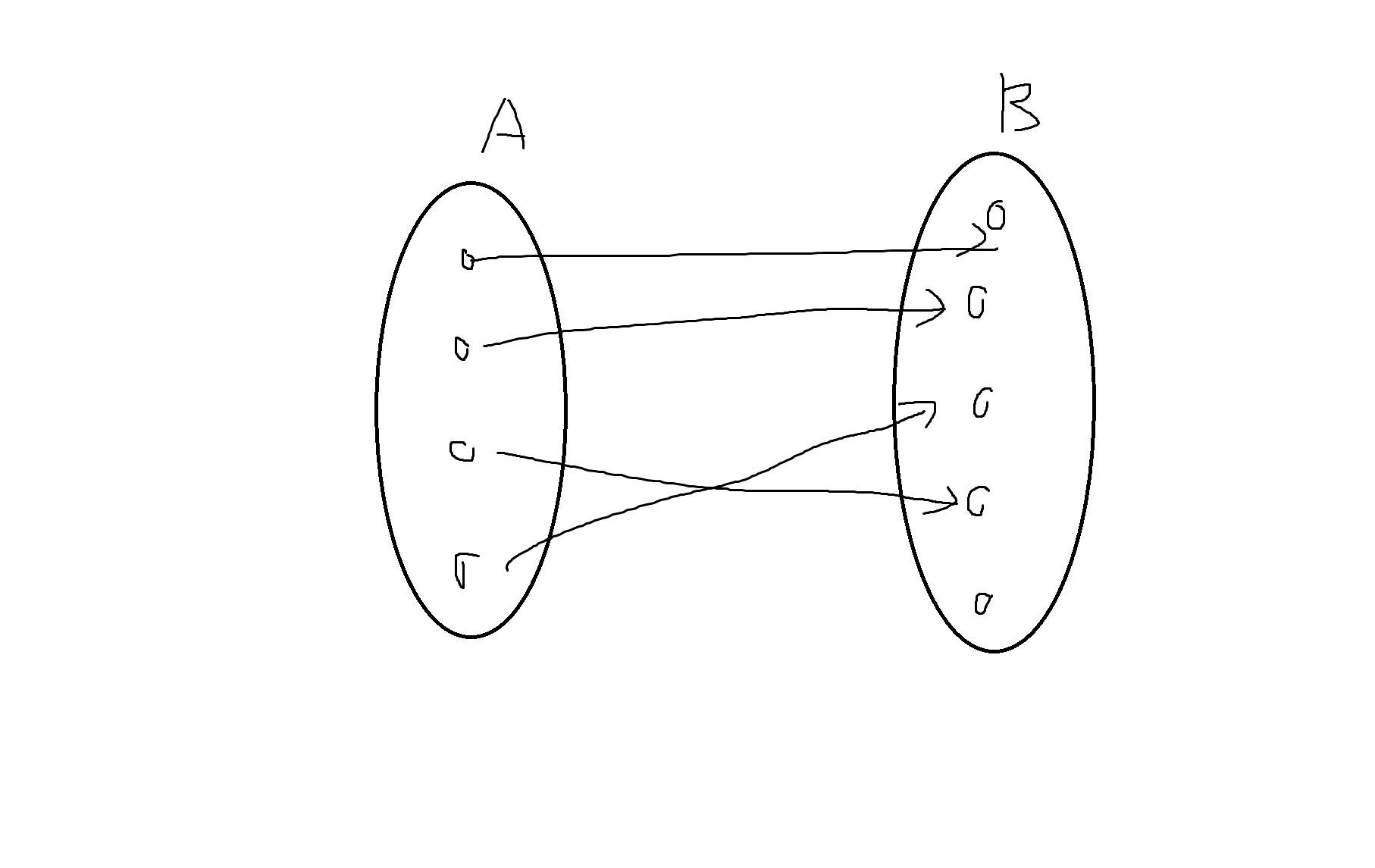
2) f가 전사함수의 경우에 그와 반대로 B의 모든 원소가 A의 원소와 대응되어야 하므로 A의 원소와 B의 원소의 개수를 비교하면 |A| >= |B|이 성립. 즉, A의 원소의 개수는 B의 원소의 개수보다 크거나 같아야함 (같은 것을 가리켜도 됨. 다만 모드 대응해야 함)
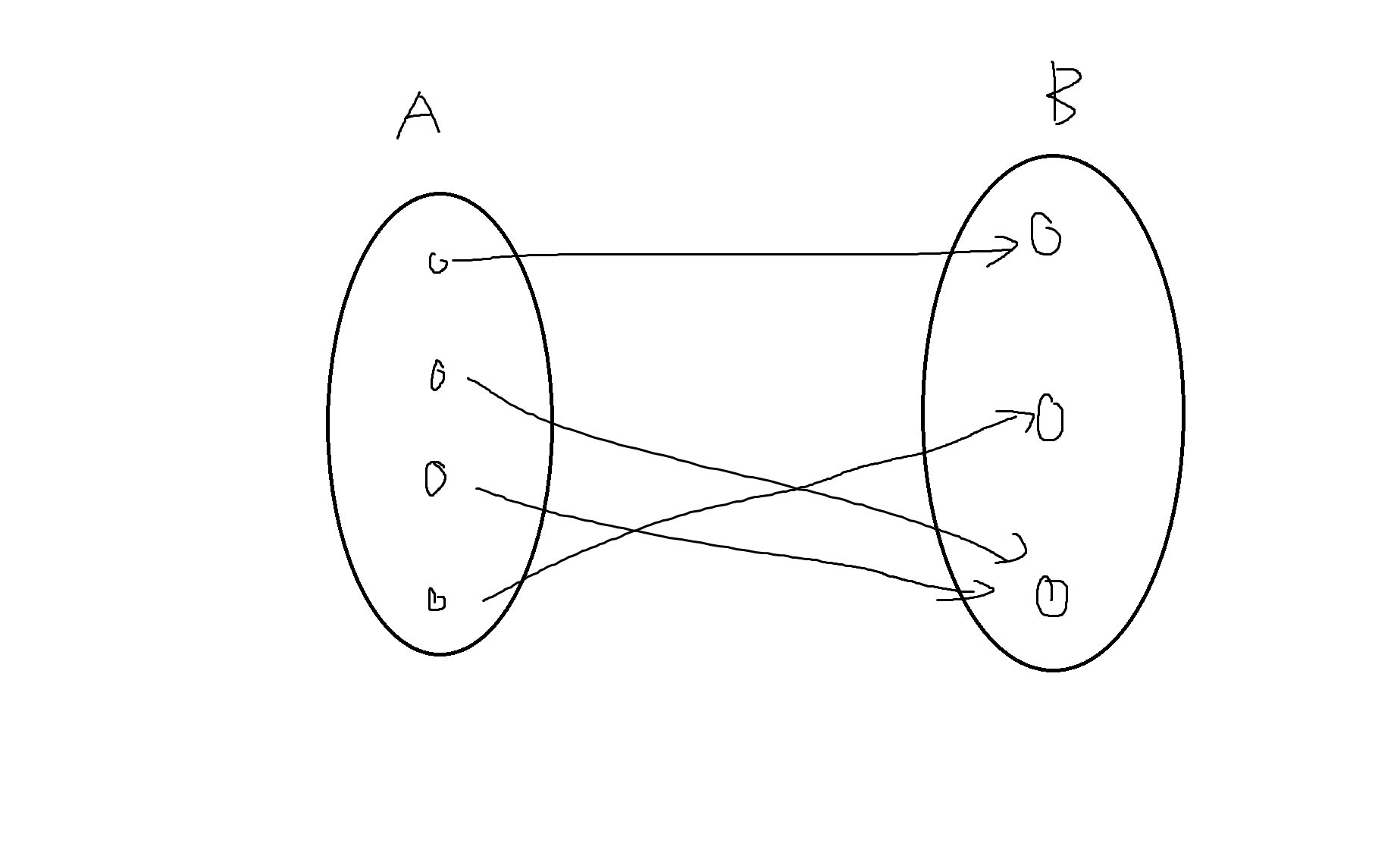
3) f가 전단사함수 -> |A| = |B|, 둘의 개수가 같음 (일대일 대응)
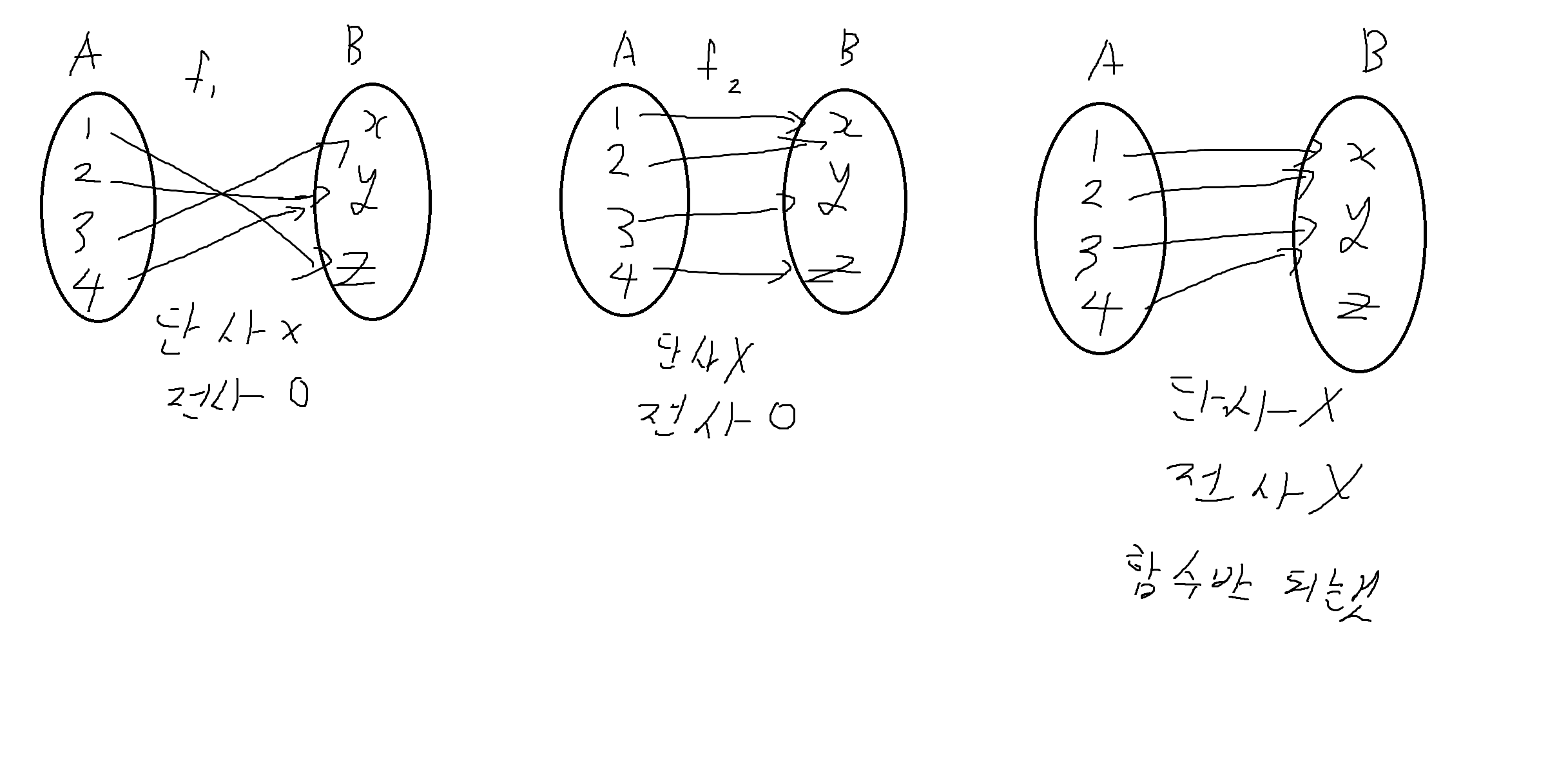
예제 6-9. f₁,f₂,f₃가 단사, 전사, 전단사 함수 여부를 판별
(1) 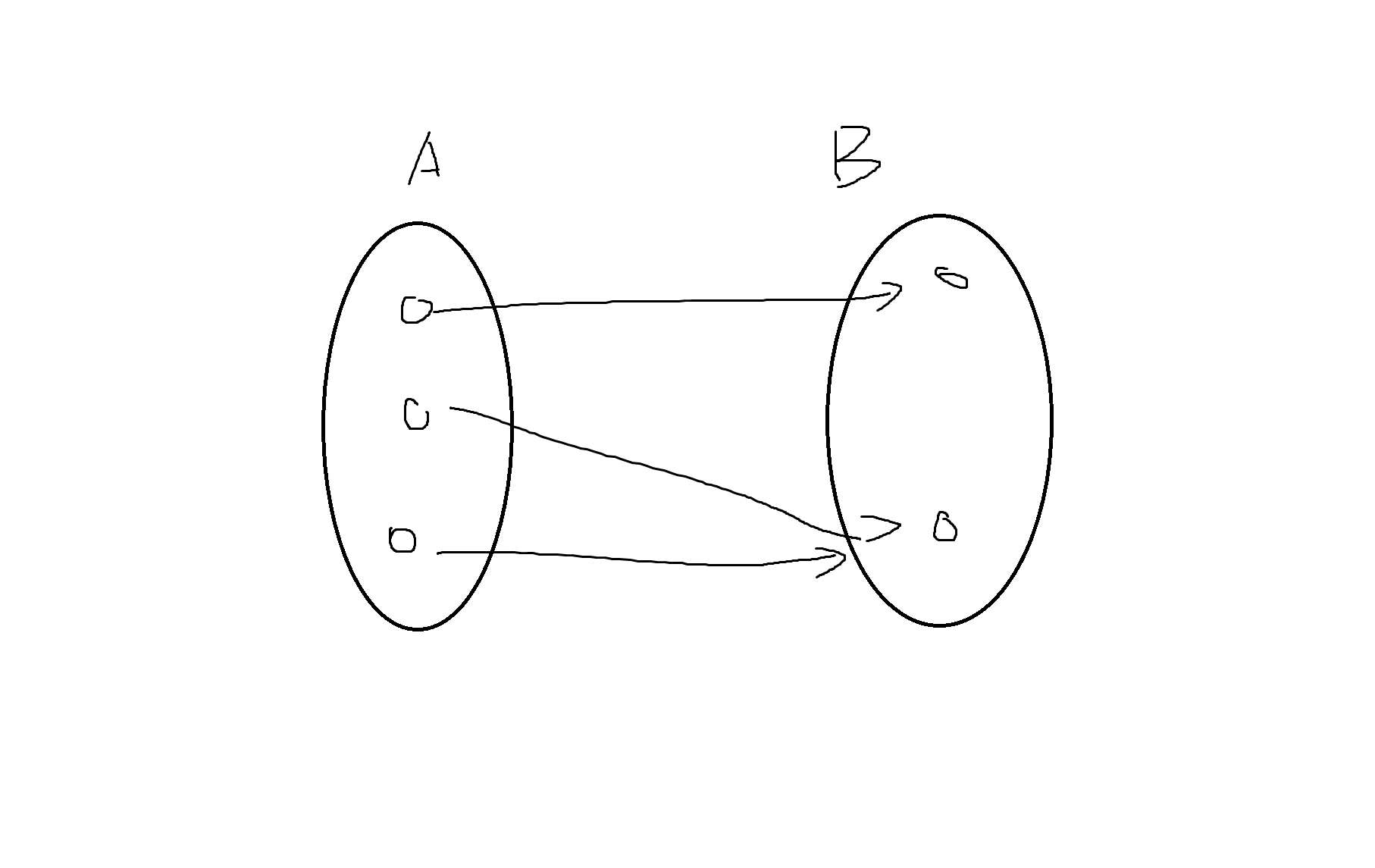
단사 X (x값이 다르면 y값도 달라야함)
전사 O (x값이 모두 대응, y중복 여부 관계 X, 공변 == 치역)
전단사 X
(2)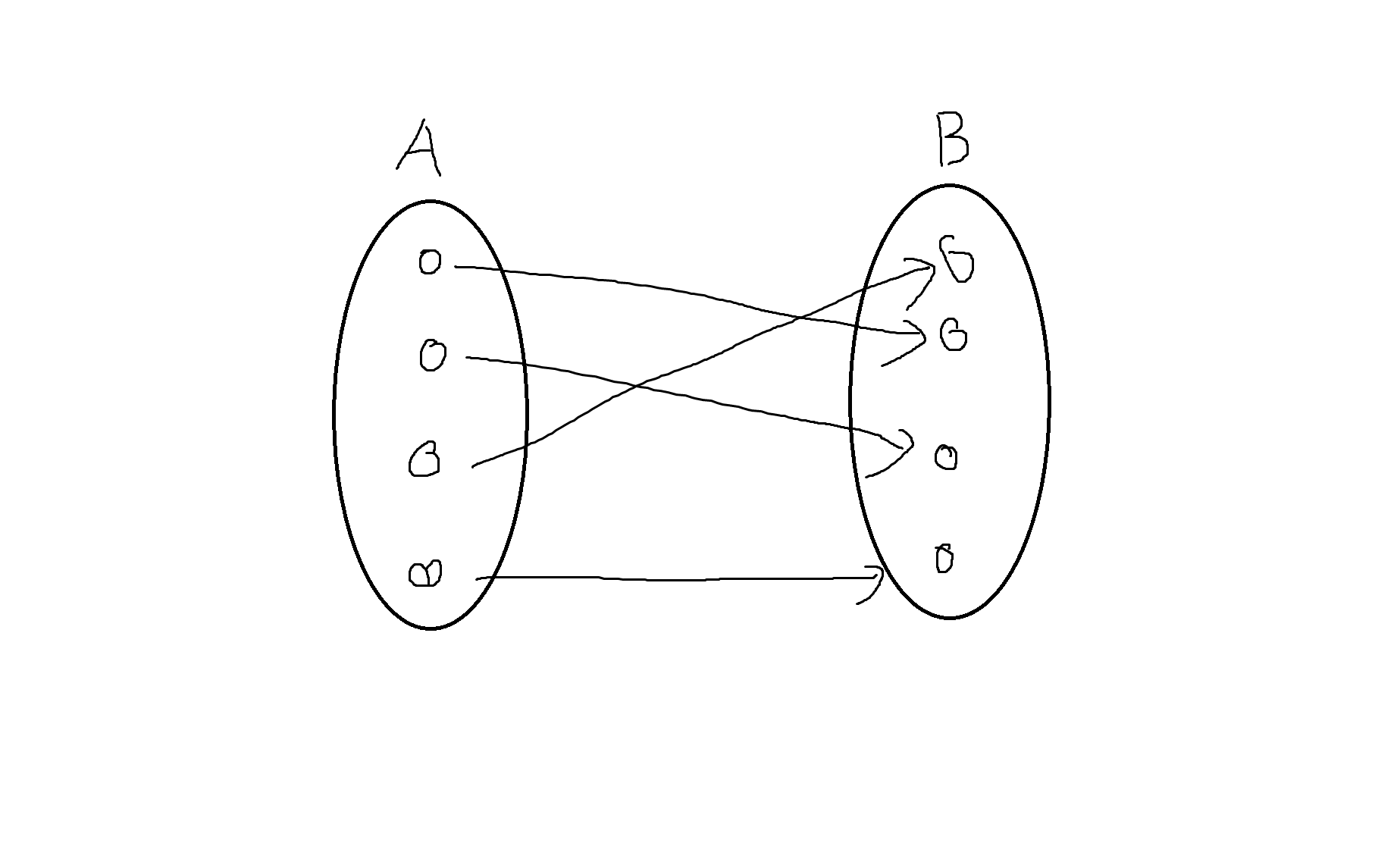
단사 O (x에 대응하는 y값이 모두 다름)
전사 O (x값 모두 대응, 공변 == 치역)
전단사 O
(3) 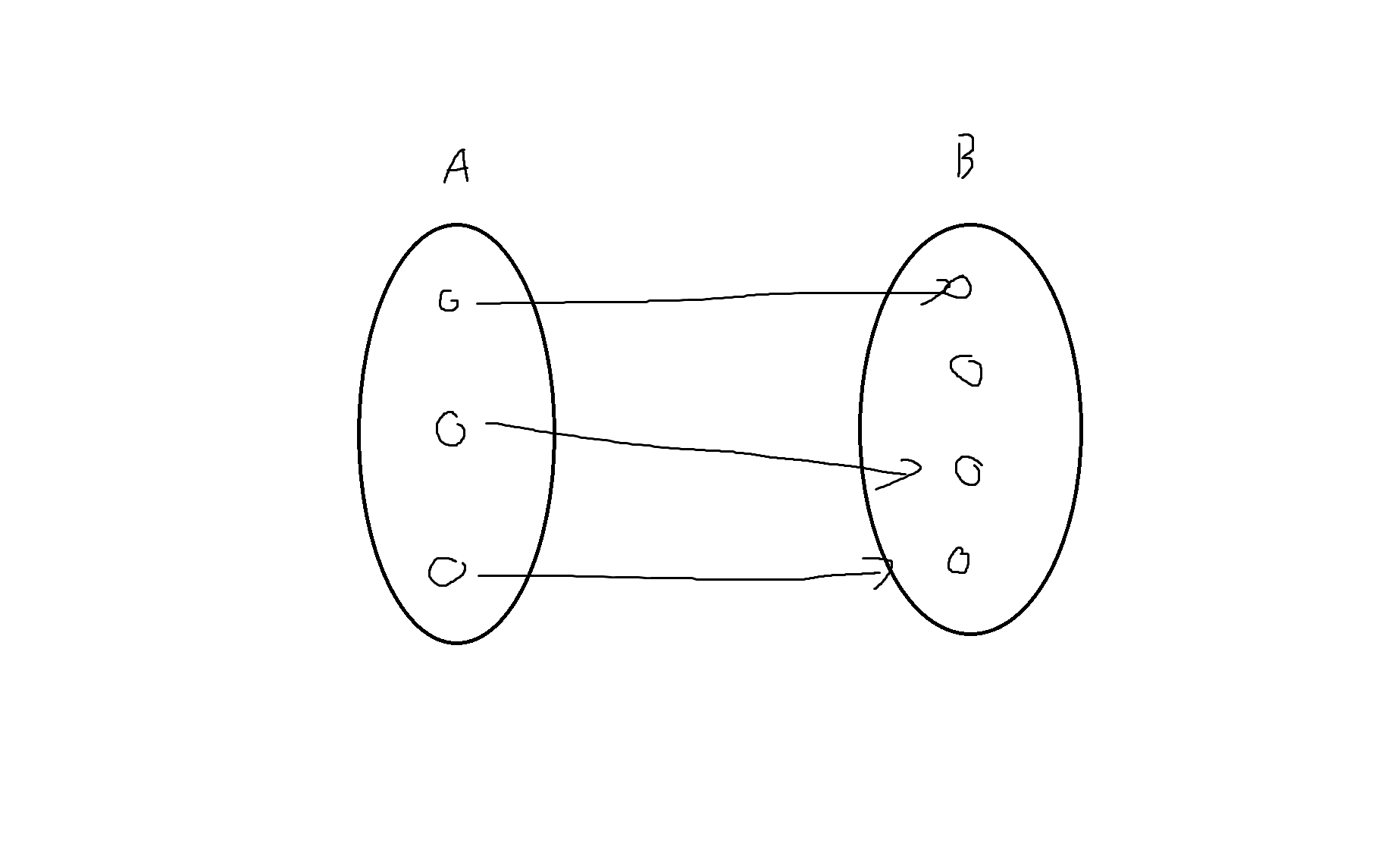
단사 O (x에 대응하는 y값 모두 다름
전사 X (공변 != 치역이므로 전사 X)
전단사 X
예제 6-10. 대한민국 국적을 가진 사람과 자신의 주민등록번호와의 관계
-> 단사O (사람(x)마다 모두 다른 값(y)), 전사O (모두 다 대응, 대응되지 않는 번호는 없음(공변==치역)), 전단사 O
예제 6-11. A = {1,2,3}, B = {1,2,3,4,5} 일때 f = {(1,1), (2,3), (3,4)}, g = {(1,1), (2,3), (3,3)}라고 하면 A에서 B로의 함수 f와 g가 각각 단사함수가 되는지 살펴봐라.
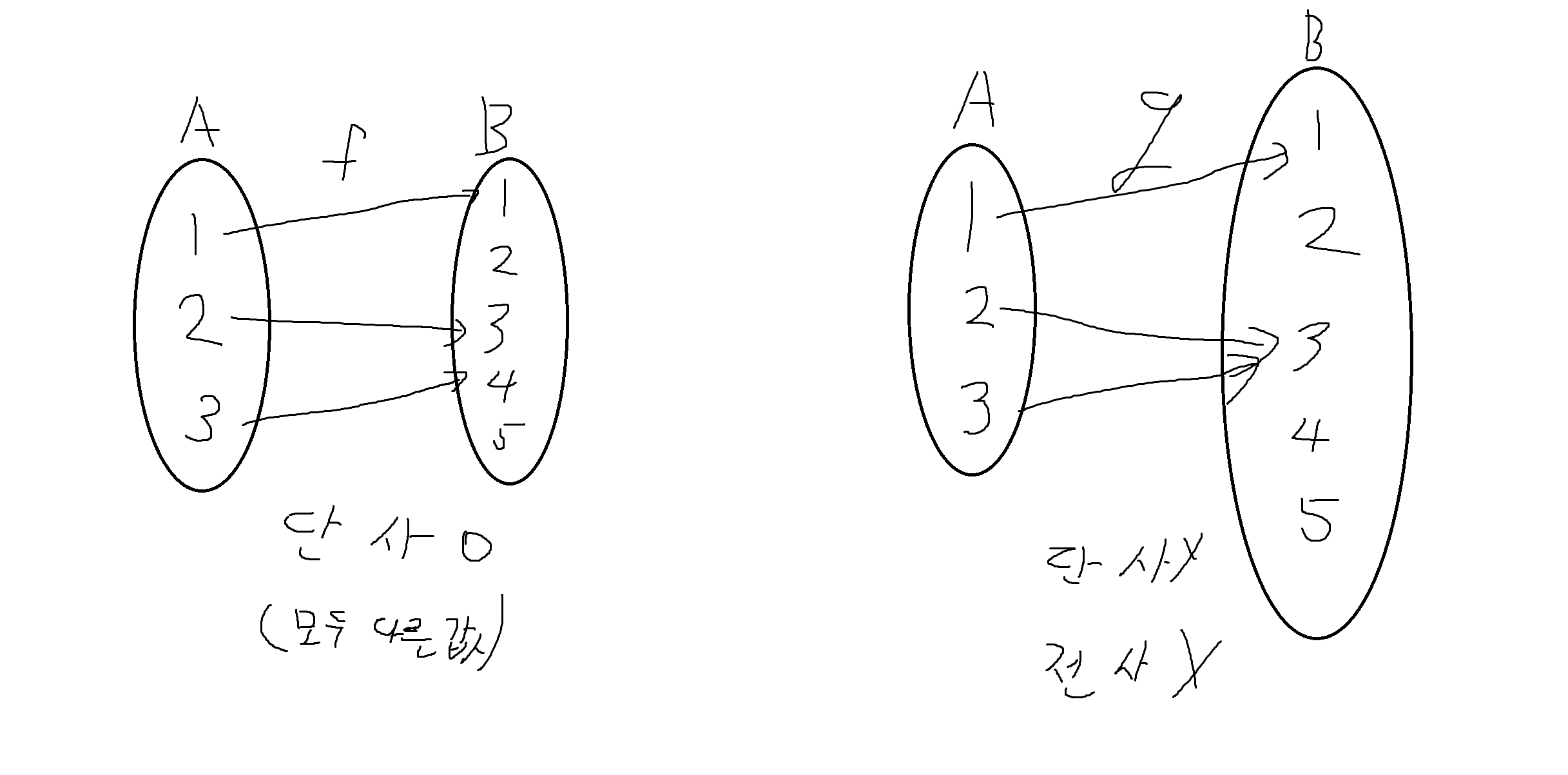
예제 6-12. A = {1,2,3,4}, B = {x,y,z}이고, f₁,f₂,f₃가 아래와 같은 각 함수가 전사함수가 되는가?
f₁ = {(1,z), (2,y), (3,x), (4,y)}
f₂ = {(1,x), (2,x), (3,y), (4,z)}
f₃ = {(1,x), (2,x), (3,y), (4,y)}
예제 6-13. 다음 함수식들이 실수 R에서 R로의 함수일때, 이 함수가 단사, 전사, 전단사 함수인지를 판별해보자
(1) f₁(x) = sin x
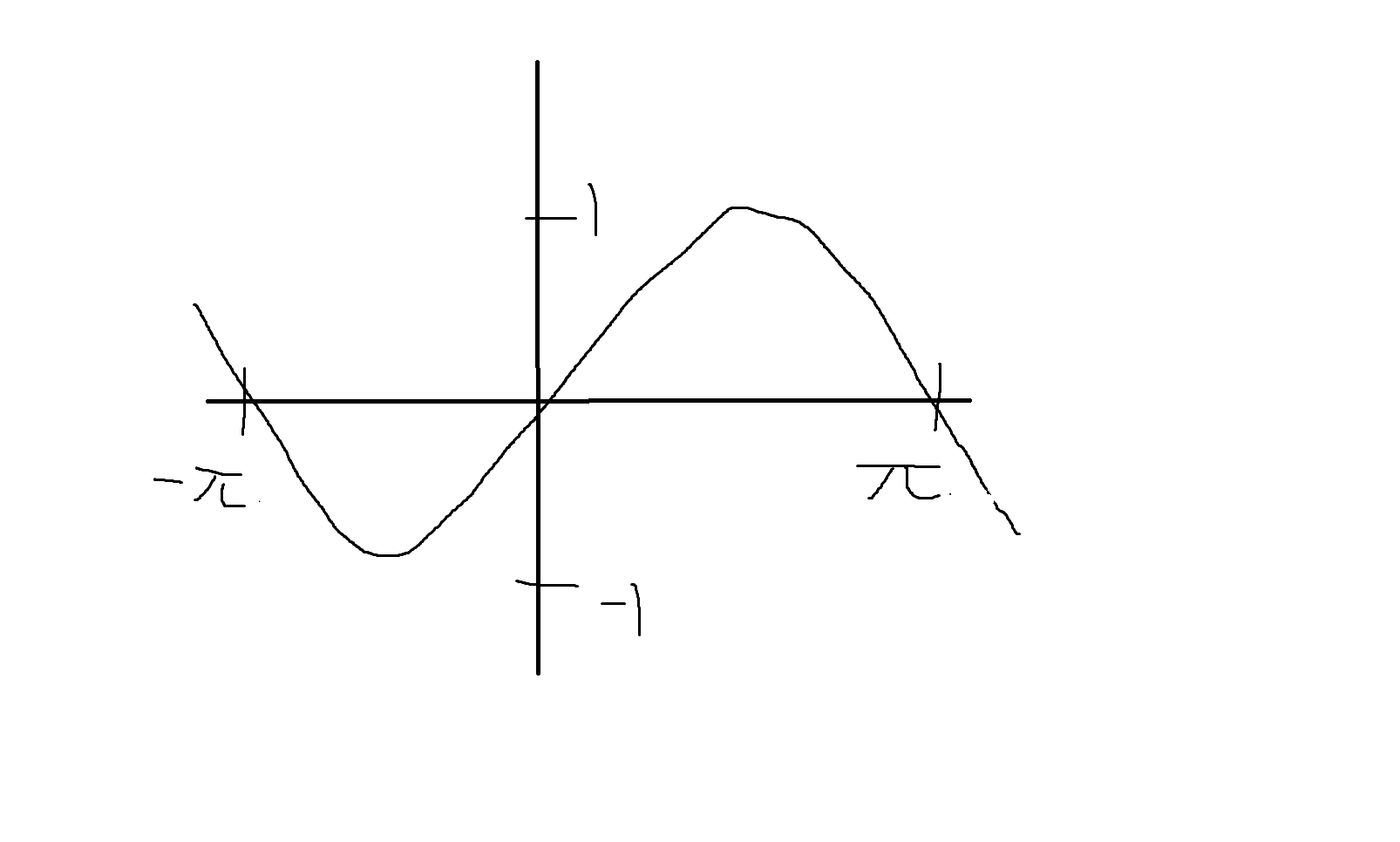
단사 X (-파이와 +파이에서 중복되는 값이 생김)
전사 X (공변역 = y축 전체, 치역 = -1 ~ 1까지 -> 둘이 다르니 전사 X)
전단사 X
(2) f₂(x) = x²
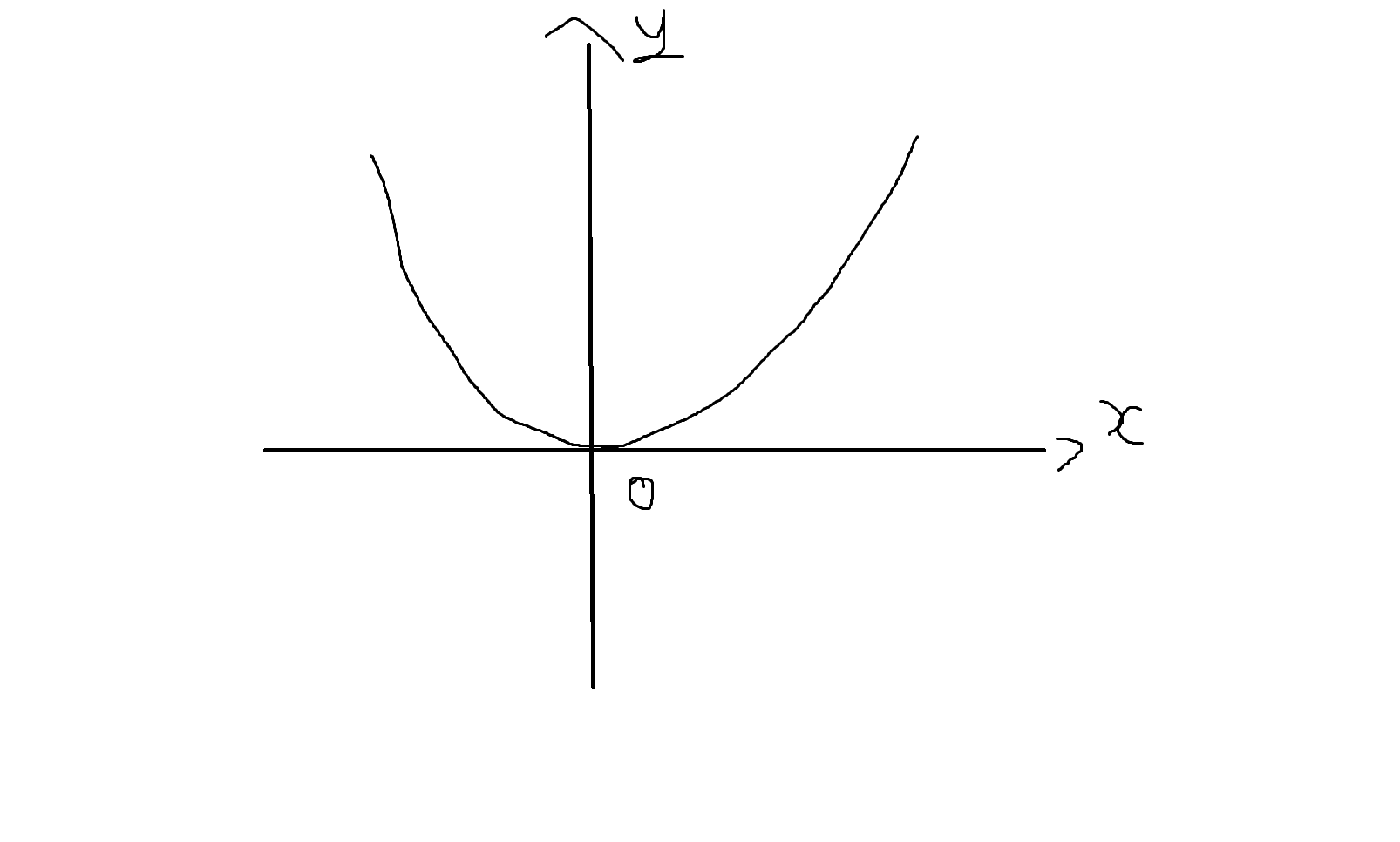
단사 X
전사 X (공변역 y축 전체, 치역 0이상)
전단사 X
(3) f₃(x) = 2^x
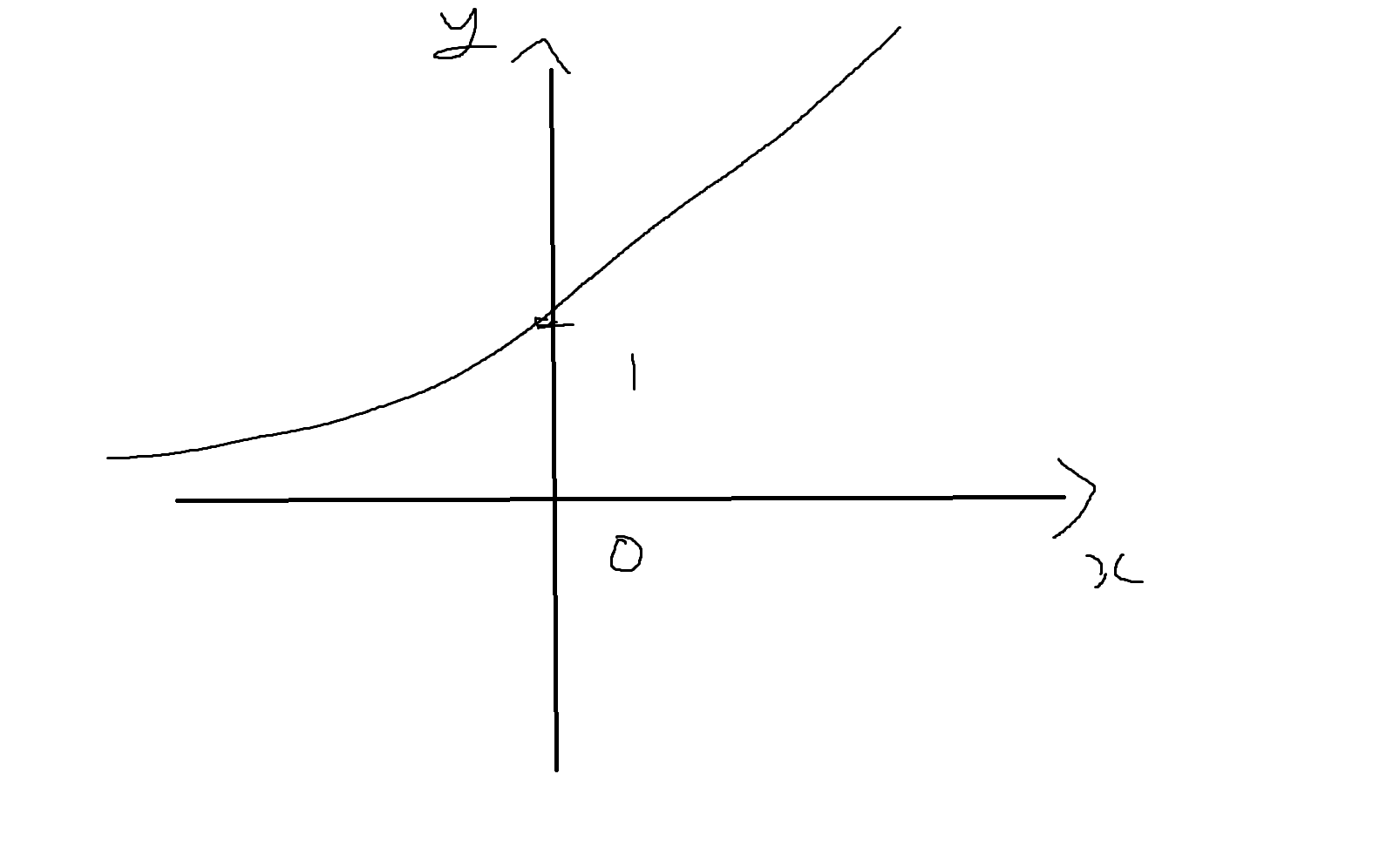
단사 O
전사 X (위와 마찬가지)
전단사 X
(4) f₄(x) = x³+2x²
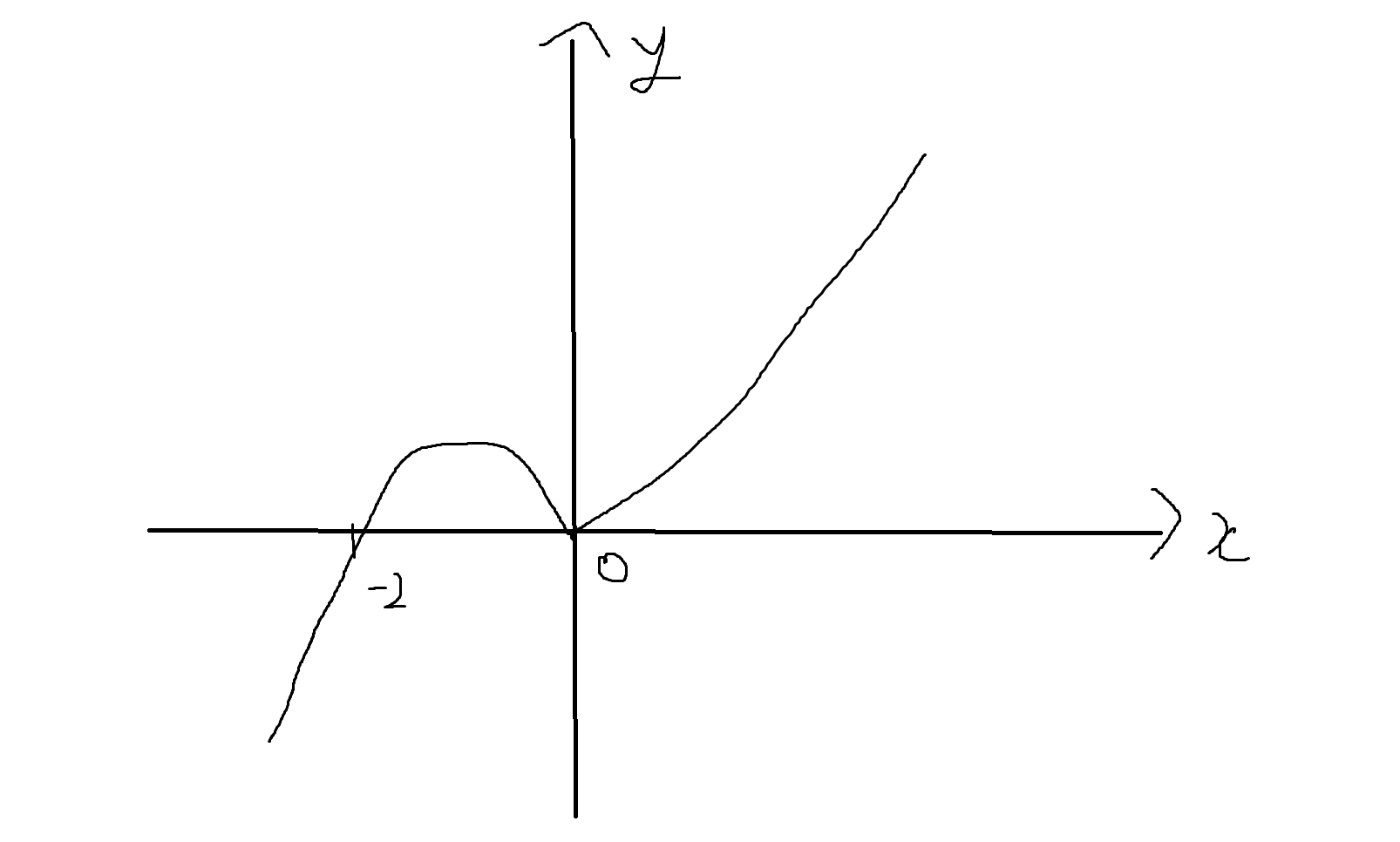
단사 X (x가 -2, 0일때 0으로 중복)
전사 O
예제 6-14. 단사, 전사, 전단사 판별하라.
(1) f: N->N이고, f(x) = 2x
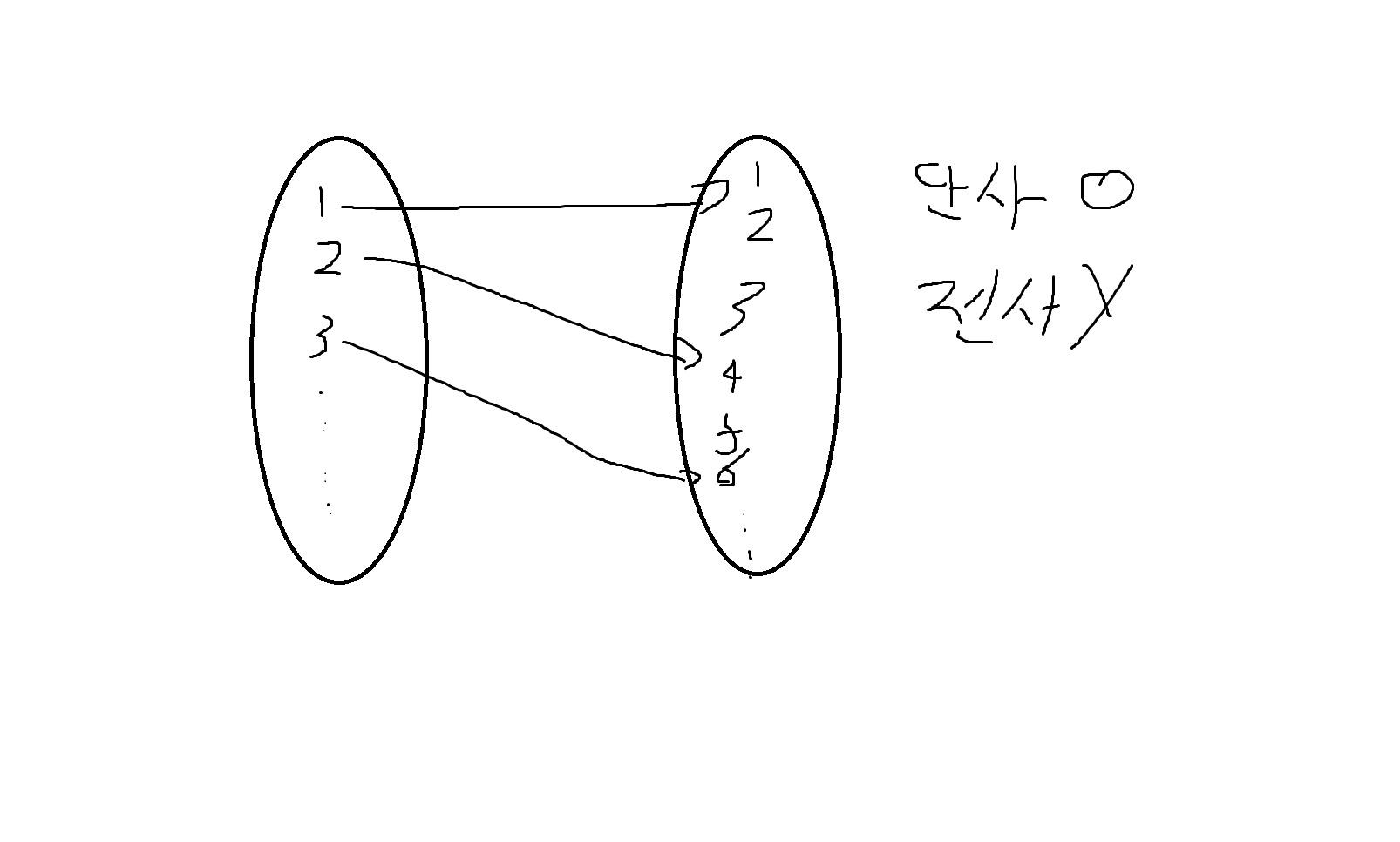
(2) f: {1,2} -> {0}
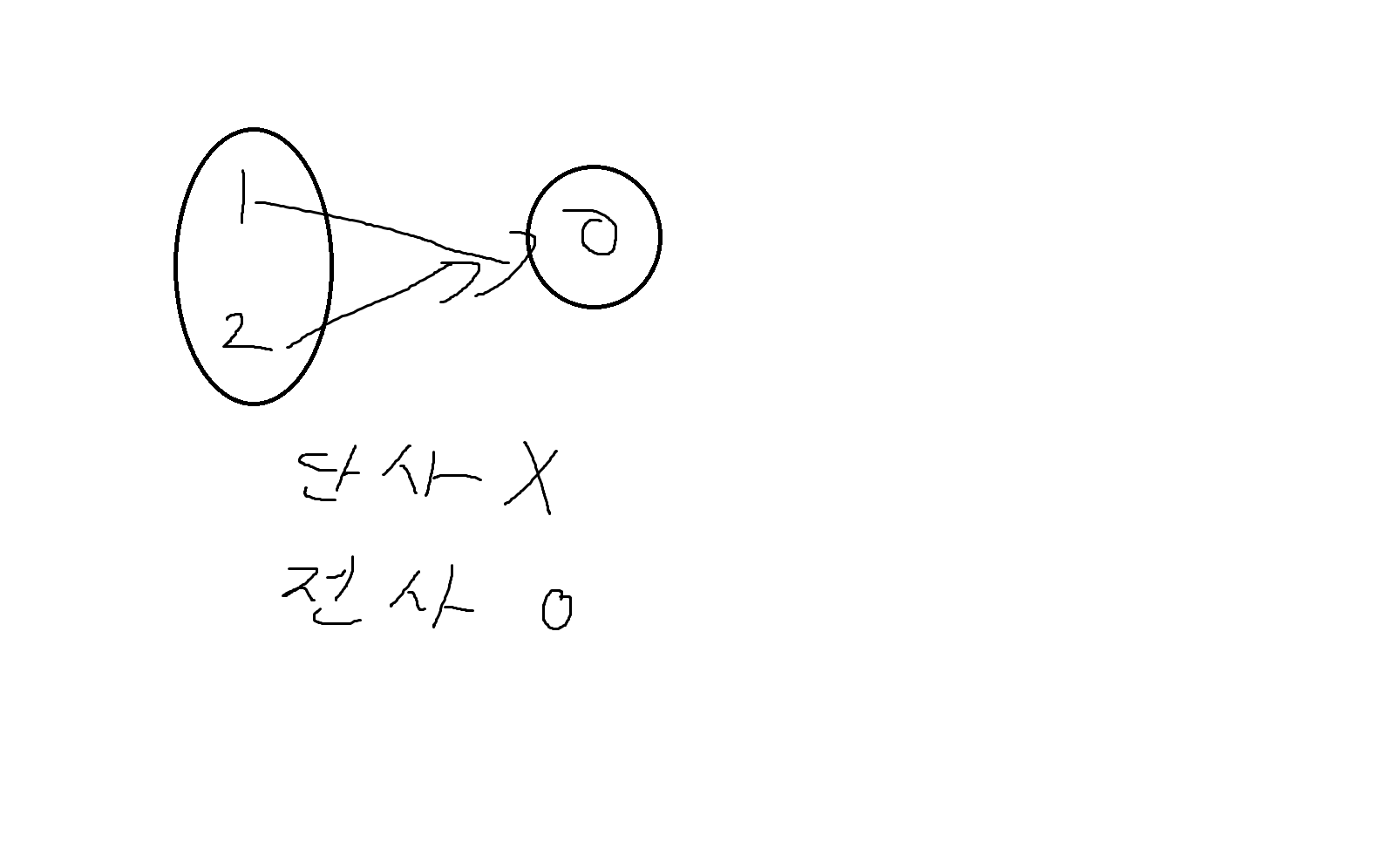
(3) f:{a,b} -> {2,4,6}이며 f(a) = 2, f(b) = 6
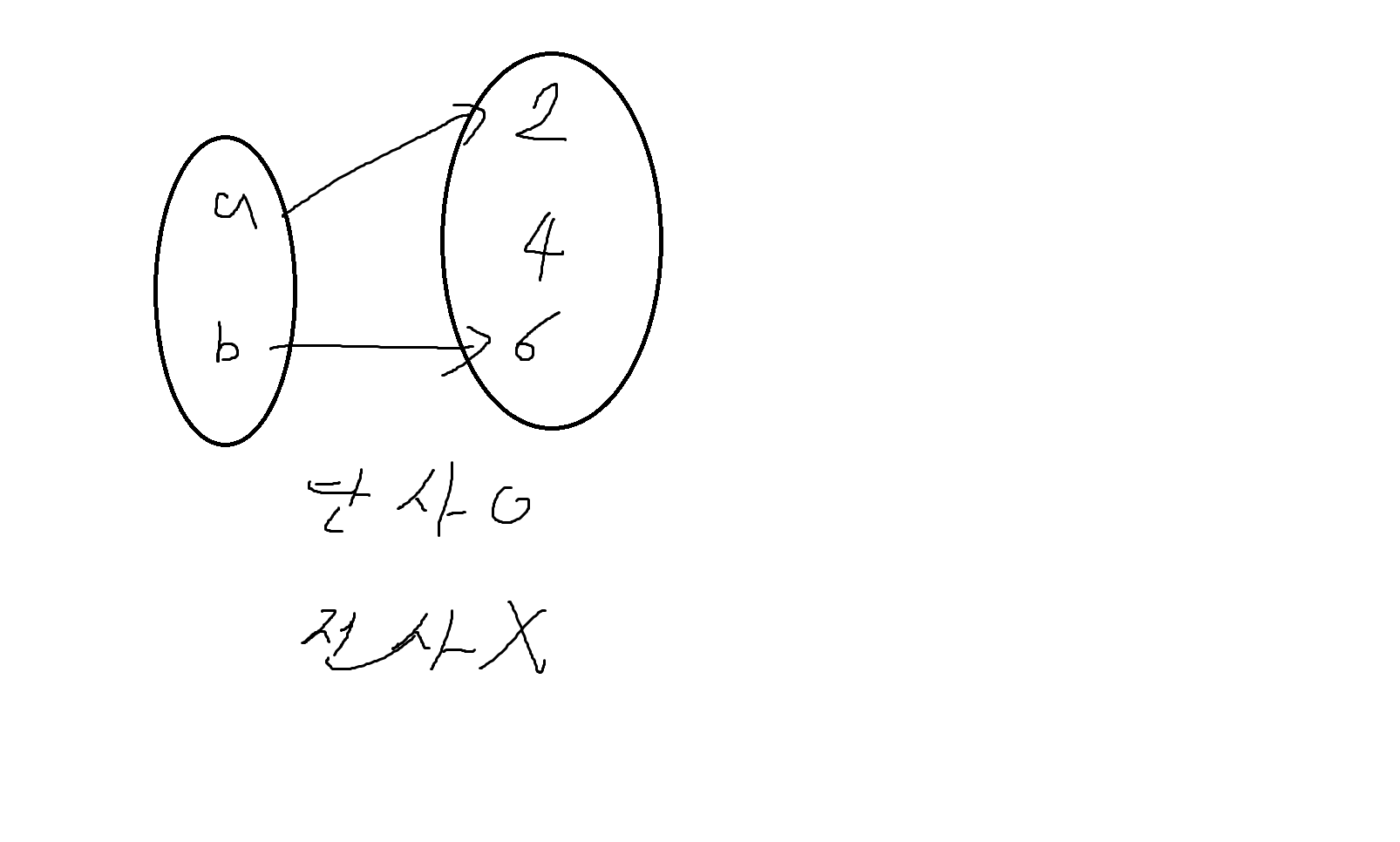
(4) f: z->z이고, f(x) = x+1
연습문제
(1) 집합 A = {a,b,c}일때, 다음의 관계가 단사, 전사, 전단사 함수인지 판별, 함수이면 정의역 공변역 치역을 구하시오
{(a,a), (b,b), (c,c)}
a -> a
b -> b
c -> c
단사 O (x가 다를때 y 다른값)
전사 O (공변 == 치역)
전단사 O
정의역 == 공변역 == 치역 == {a,b,c}
(2) X = {1,2,3}에서 Y = {a,b,c}로의 함수가 단사, 전사, 전단사 함수인지를 판별해라.
f = {(1,a), (2,c), (3,b)}
단사 O
전사 O (공변 == 치역)
전단사 O
(3) X = {1,2,3}에서 Y = {a,b,c}로의 함수가 단사, 전사, 전단사 함수인지를 판별하고, 함수이면 정의역, 공변역, 치역을 구하시오.
f = {(1,a), (2,c), (3,b}
단사 O
전사 O
전반사 O
정의역 == {1,2,3}
공변역 == 치역 == {a,b,c}
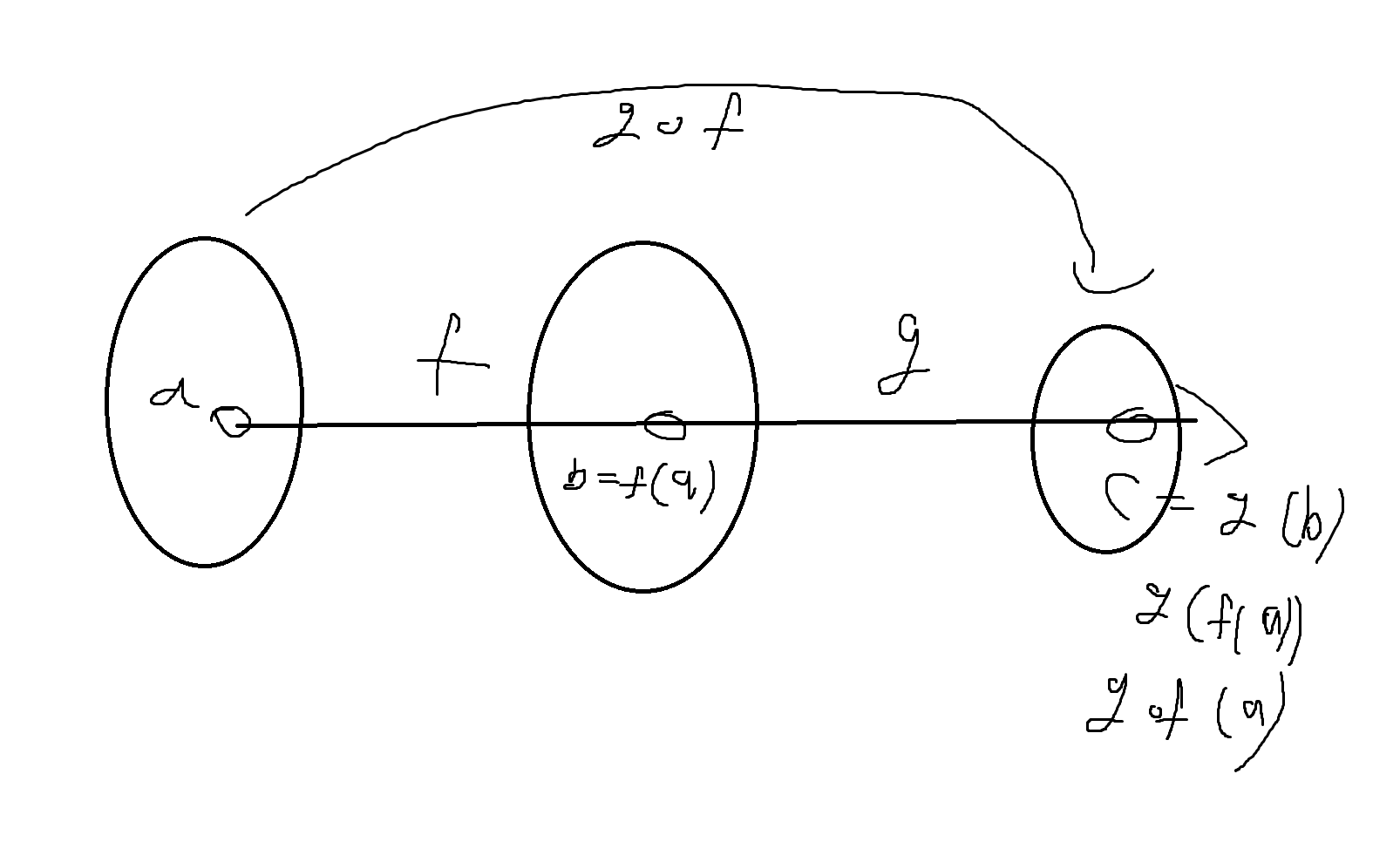
정의 6-6. 두 함수 f: A->B, g: B->C에 대하여 두 함수 f와 g의 합성함수는 두 집합 A에서 집합 C로의 함수, g * f : A->C를 의미하며 다음을 만족시킨다.
g * f = {(a,c)|a∈A, b∈B, c∈C, f(a)=b, g(b)=c}
두 함수 f와 g의 합성함수 g f는 A의 모든 원소 a에 대하여
∀a ∈ A, (g f)(a) = g(f(a))
함수 f,g와 합성합수 g * f에 대한 관계
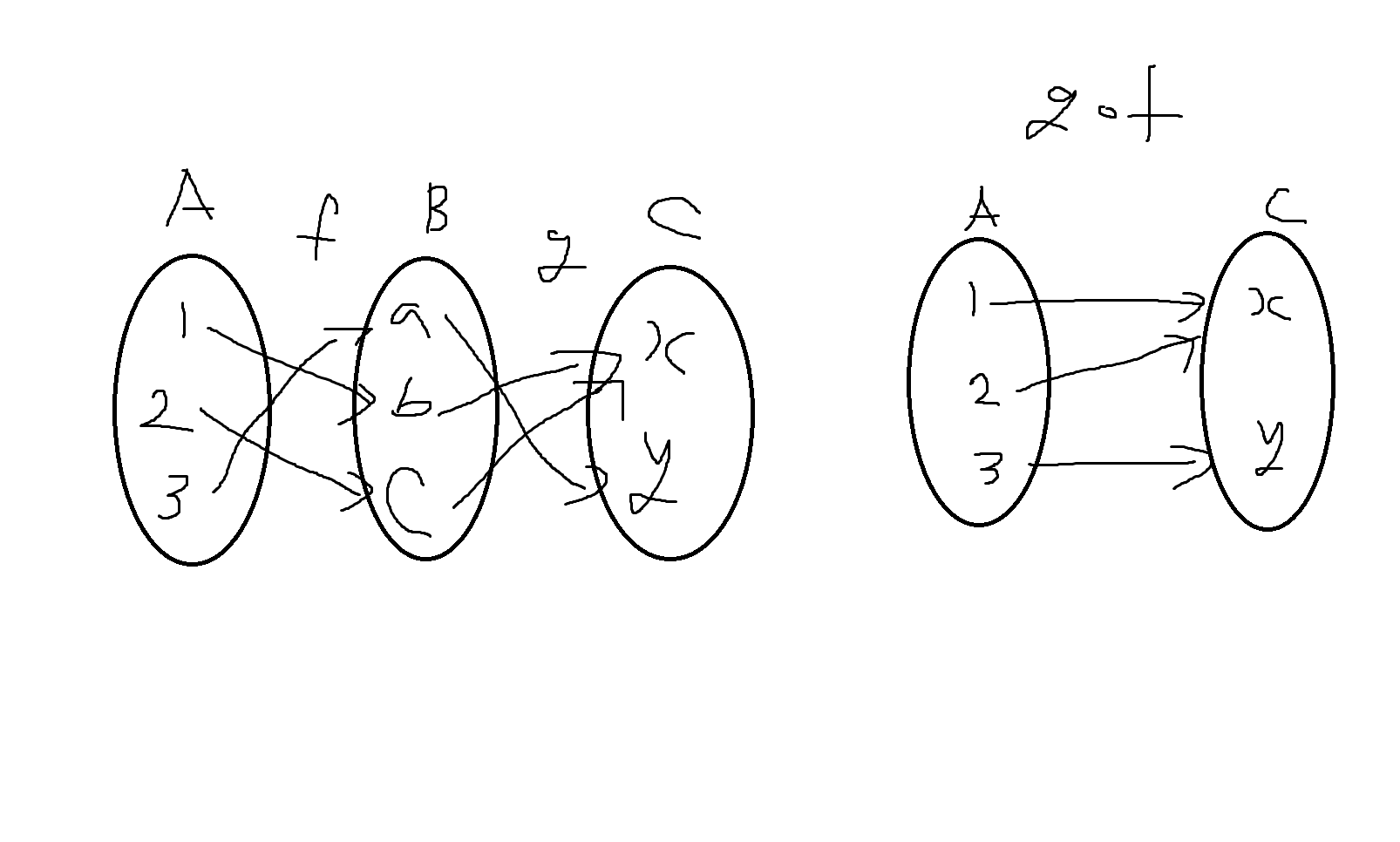
예제 6-15. f: A->B와 g: B->C가 다음 그림과 같을 때, 두 함수 f와 g의 합성함수 g * f를 구해보자
예제 6-16. A = {1,2,3,4}, B = {a,b,c,d,e}, C = {7,8,9}이고, f: A->B, g: B->C 일때 합성함수 h: A->C를 구해보자.
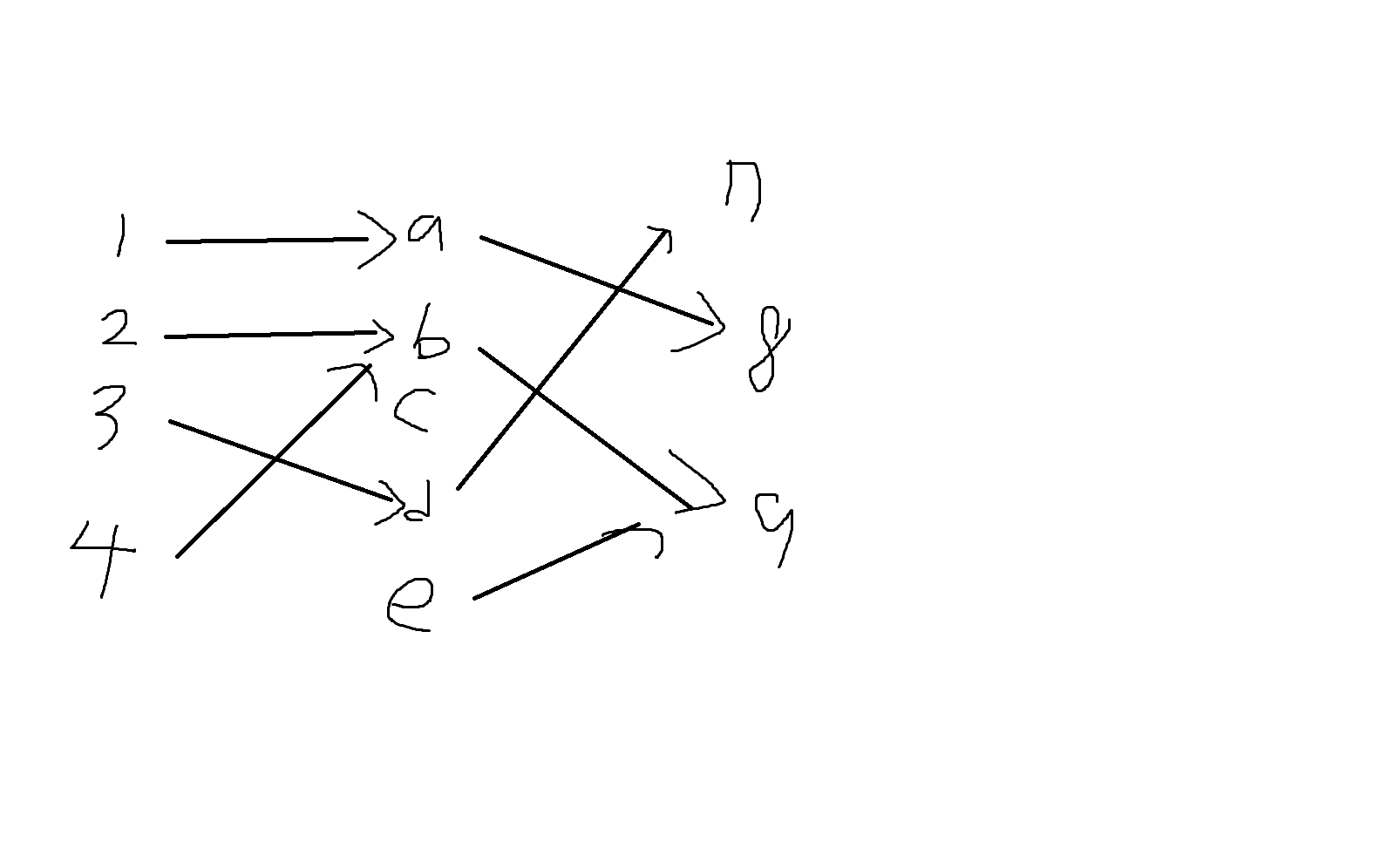
h = g * f
1->8
2->9
3->7
4->9
예제 6-17. 두 함수 f와 g가 각각 f: R->R, f(x) = x+3이고 g: R->R, g(x) = x²-1일때, 합성함수 f g, g f를 구해보자
f g = f(x²-1) = x²+2
g f = g(x+3) = x²+6x+8
정리 6-1. 세 함수 f,g,h를 각각 f: A->B, g: B->C, h: C-> D라 할 때, 그들의 합성함수는 다음과 같은 결합법칙 성립
h (g f) = (h g) f
정의 6-7. 집합 A에 대한 함수 f가 f: A->A, f(a) = a일 때 함수 f를 항등함수라고 하고 IA로 표기한다. 즉
∀a∈A, IA(a) = a이다.
- 항등함수는 x가 항상 자기자신에게 대응하기 때문에 단사함수이면서 전사함수이므로 전단사함수이다.
예제 6-18. 집합 A = {-1, 0, 1}이고 함수 f: A->A, f(x) = x³일때 함수 f는 항등함수임을 보이자.
| x | x³ |
|---|---|
| -1 | -1 |
| 0 | 0 |
| 1 | 1 |
자기 자신으로의 관계, 즉 f는 항등함수이다.
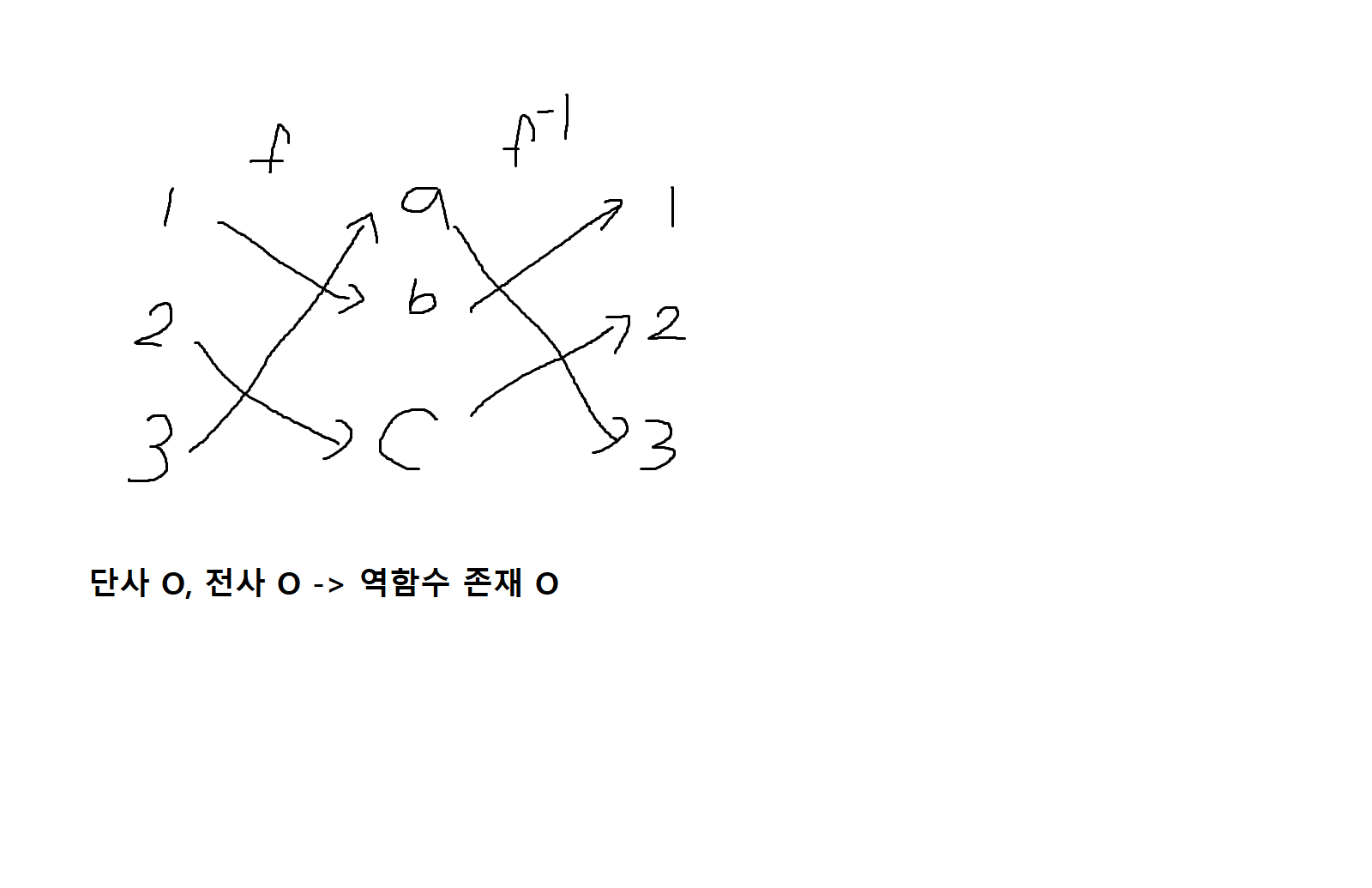
정의 6-8. 함수 f: A->B가 전단사함수일 때 f의 역함수는 f^-1 : B->A로 표기하고 다음과 같이 정의한다.
∀a ∈ A, ∀b ∈ B, f(a) = b -> f역함수 (b) = a
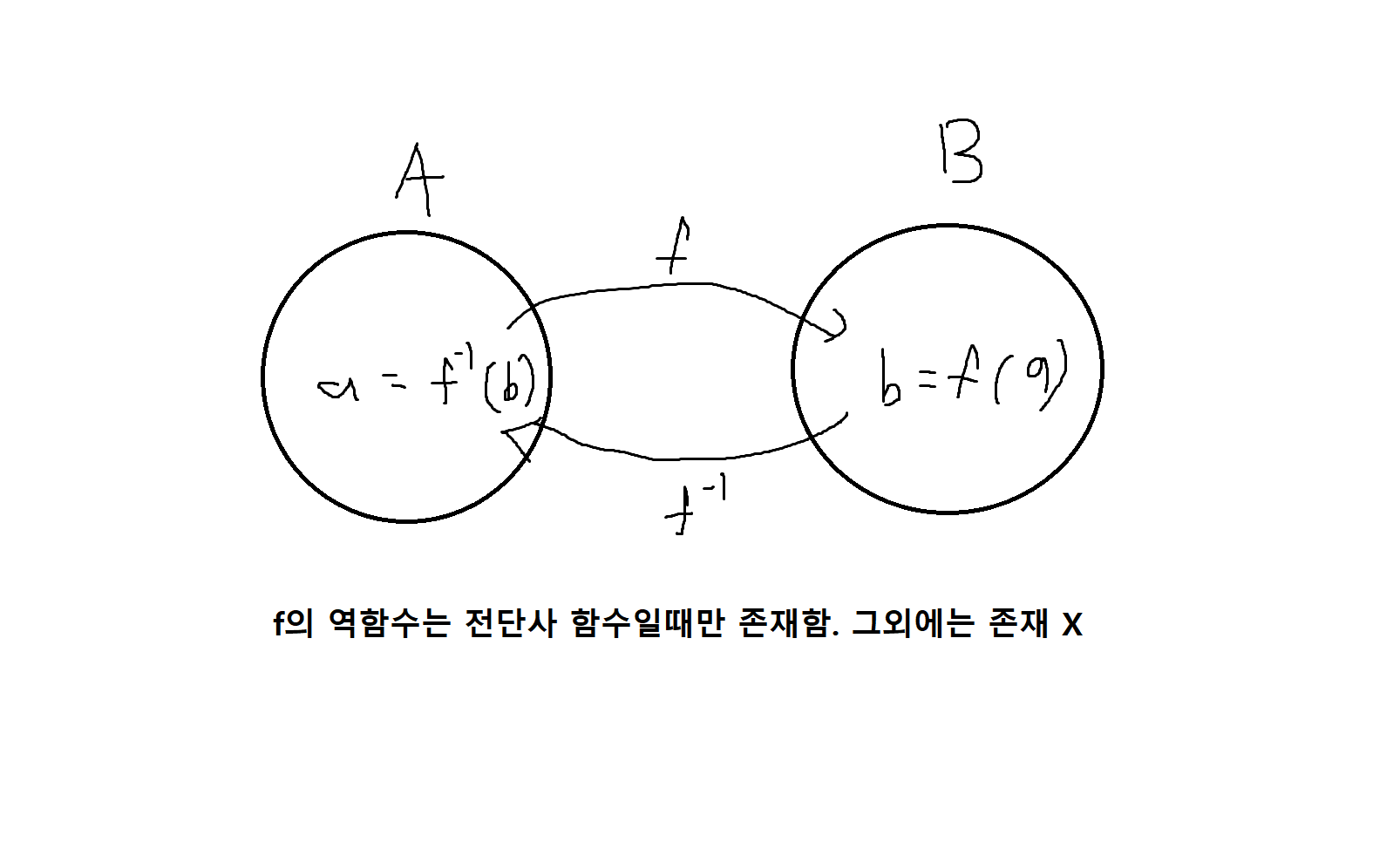
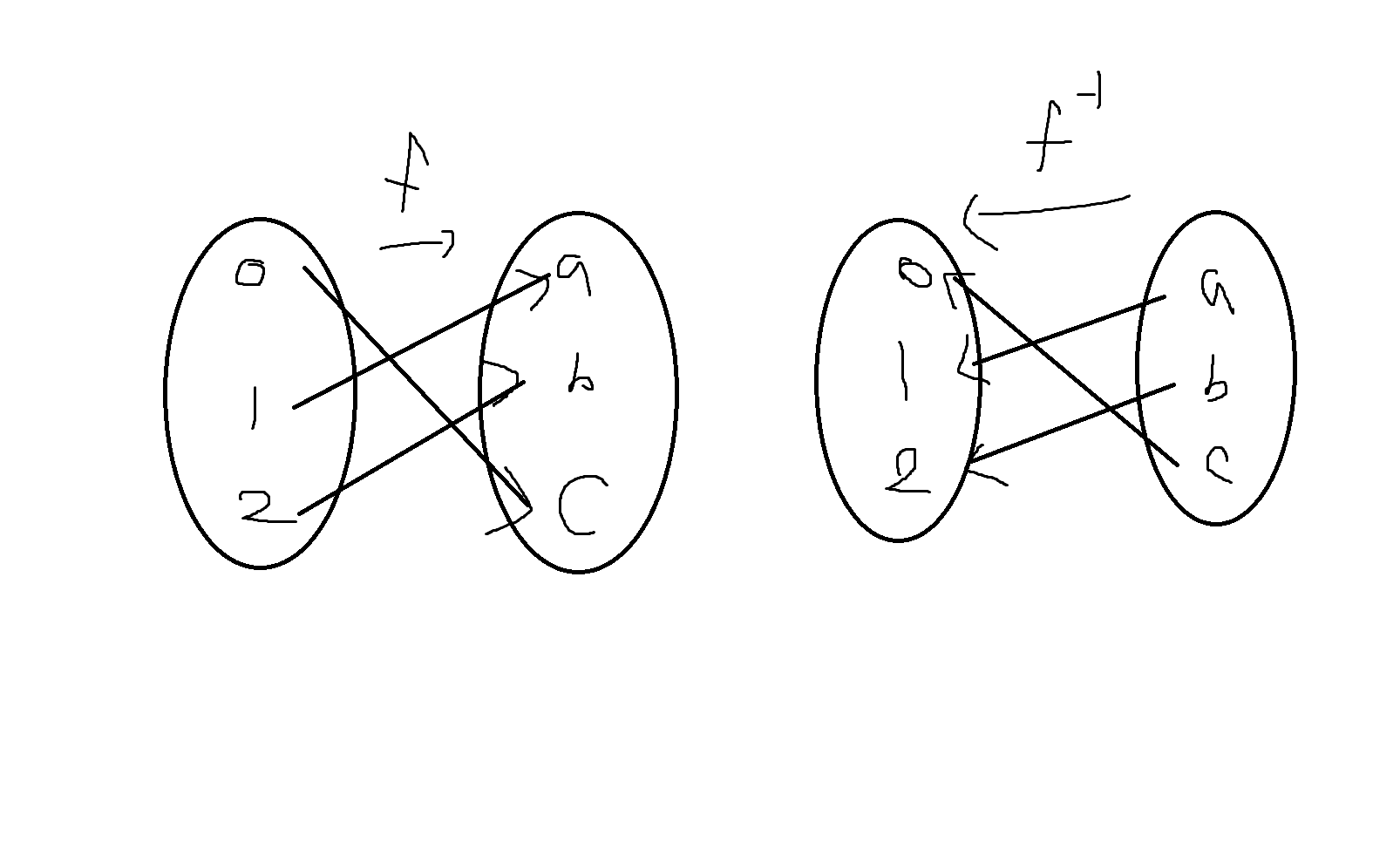
예제 6-19. f: {0,1,2} -> {a,b,c}가 다음과 같은 그래프로 정의될 경우 이에 대응하는 역함수를 구해보라
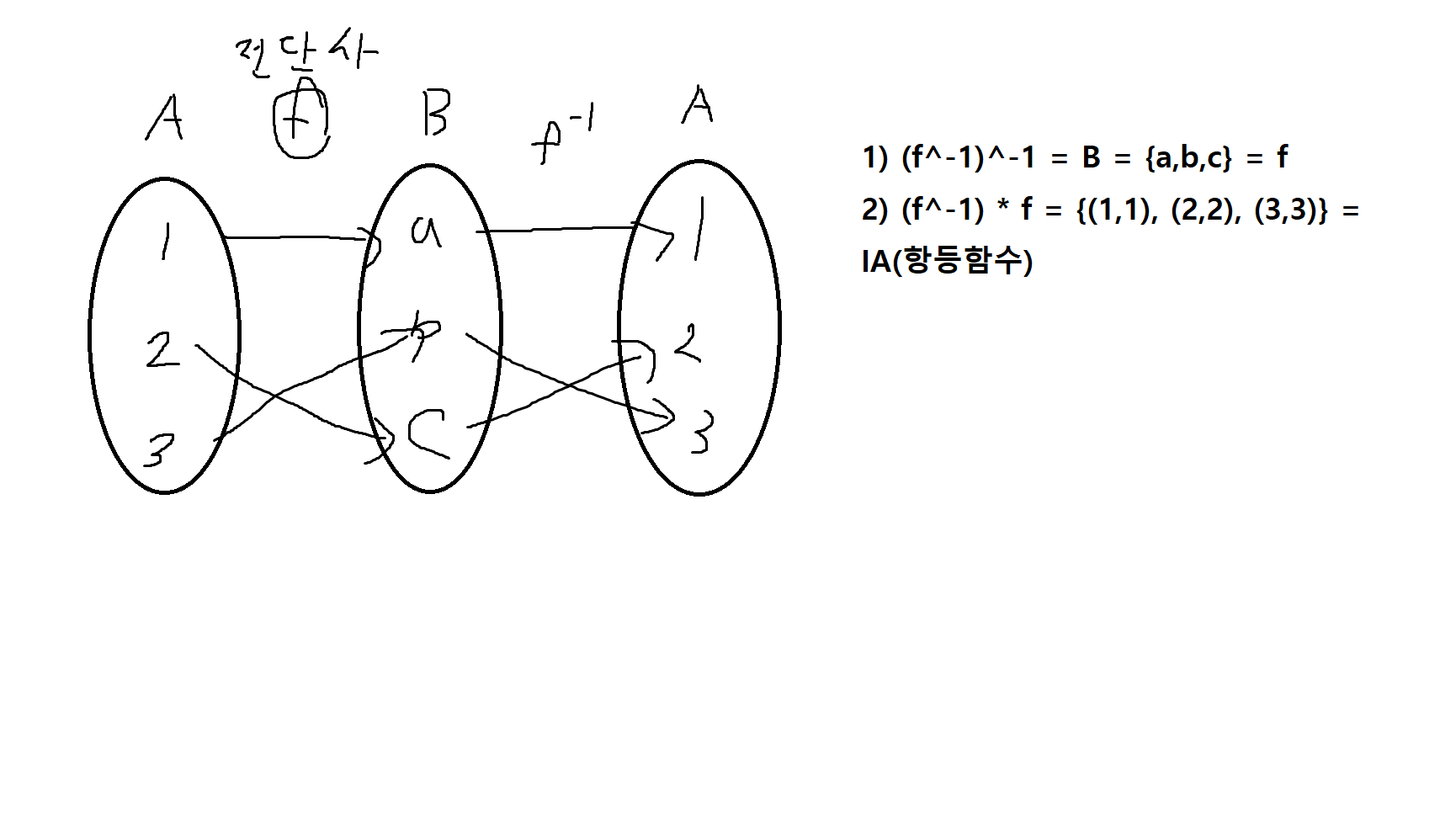
예제 6-20. 집합 A = {1,2,3}, B = {a,b,c}이고 A에서 B로의 함수 f = {(1,a), (2,c), (3,b)}일 때 f의 역함수의 역함수, f^-1 * f를(f역함수와 f의 합성함수) 구해보자
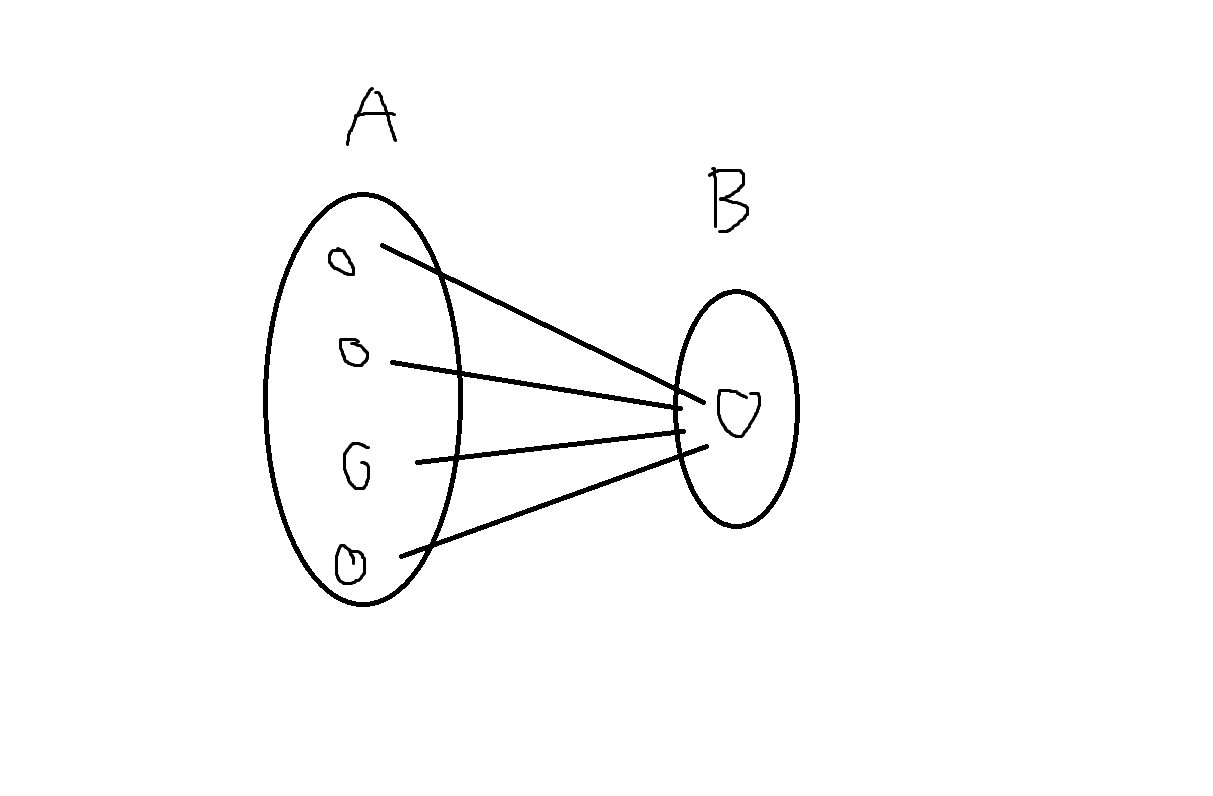
정의 6-9. 함수 f: A->B에서 집합 A의 모든 원소가 집합 B의 오직 한 요소와 대응할 때 함수 f를 상수함수라 한다. 즉, ∀a ∈ A, ∃b ∈ B, f(a) = b이다.
정의 6-10. 전체 집합 U의 부분집합 A의 특성함수, fA: U -> {0,1}는 다음과 같이 정의된다.
fA(x) = 0 (if x !∈ A), 1 (if x ∈ A)
- 특성함수에 포함되면 1, 포함되지 않으면 0
예제 6-22. 집합 U = {x∈R | 0<=x<=1}이고 A = {x∈R | 0<=x<=1/2}일때, 특성함수 fA를 그래프로 나타내보자
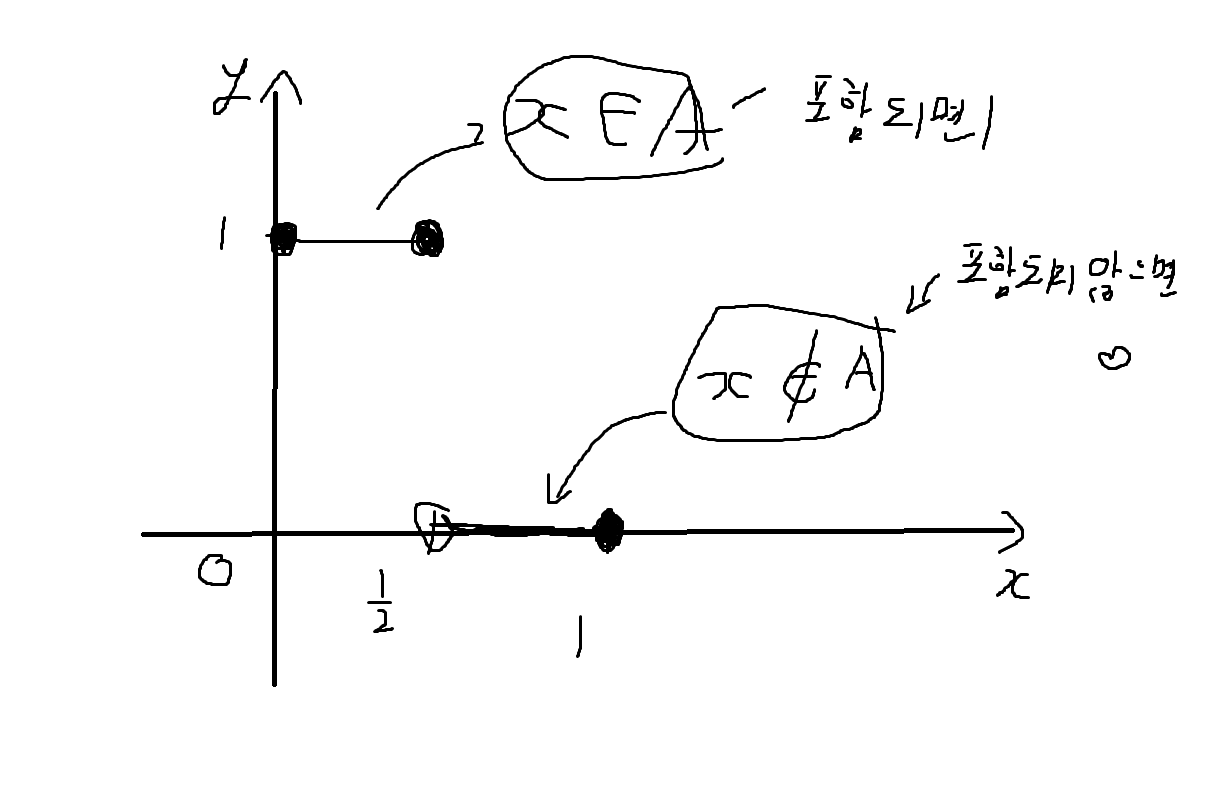
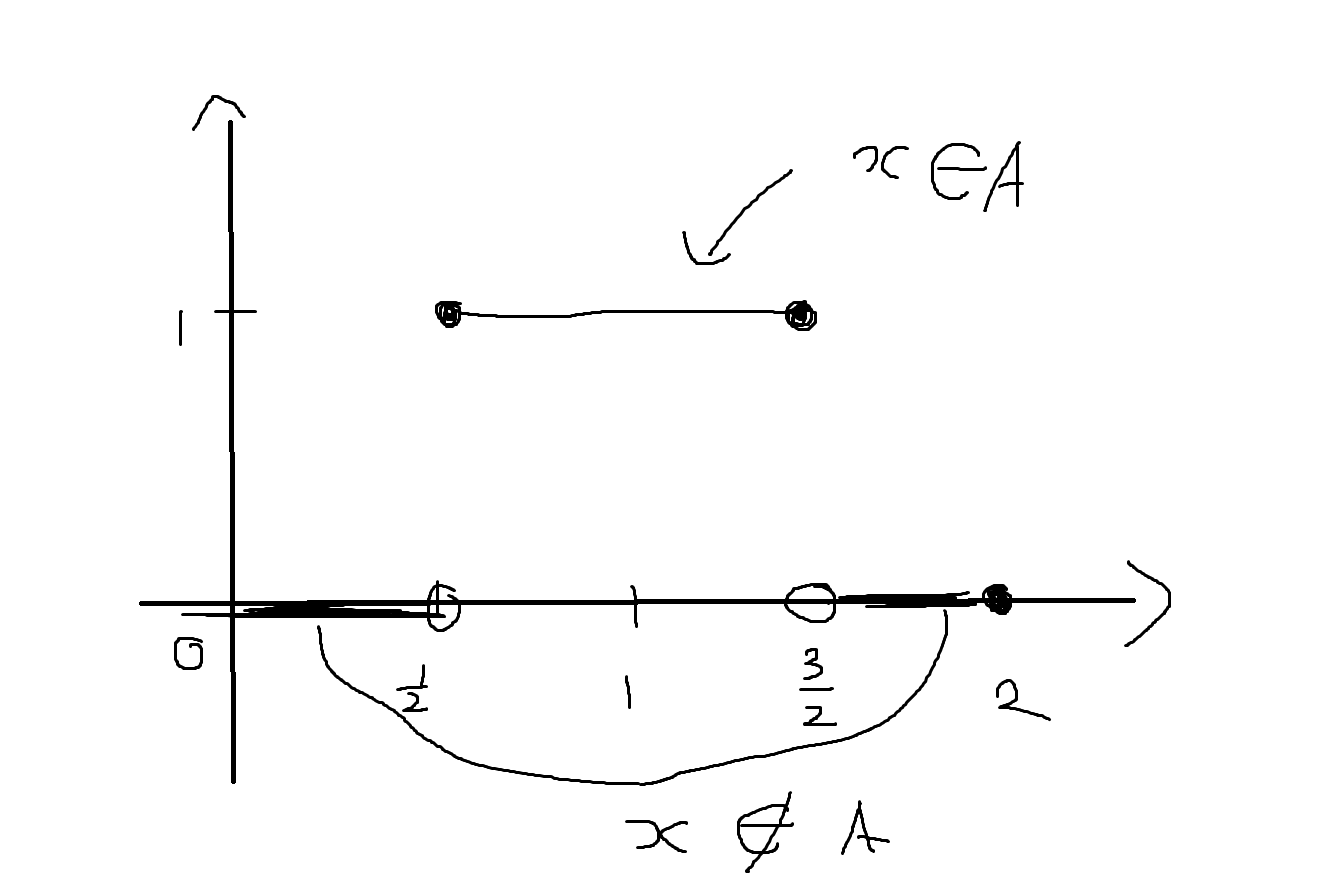
예제 6-23. 집합 U = {x ∈ R | 0<=x<=2}이고 A = {x∈R | 1/2 <= x <= 3/2} 일때, 특성함수 fA를 그래프로 나타내보자.
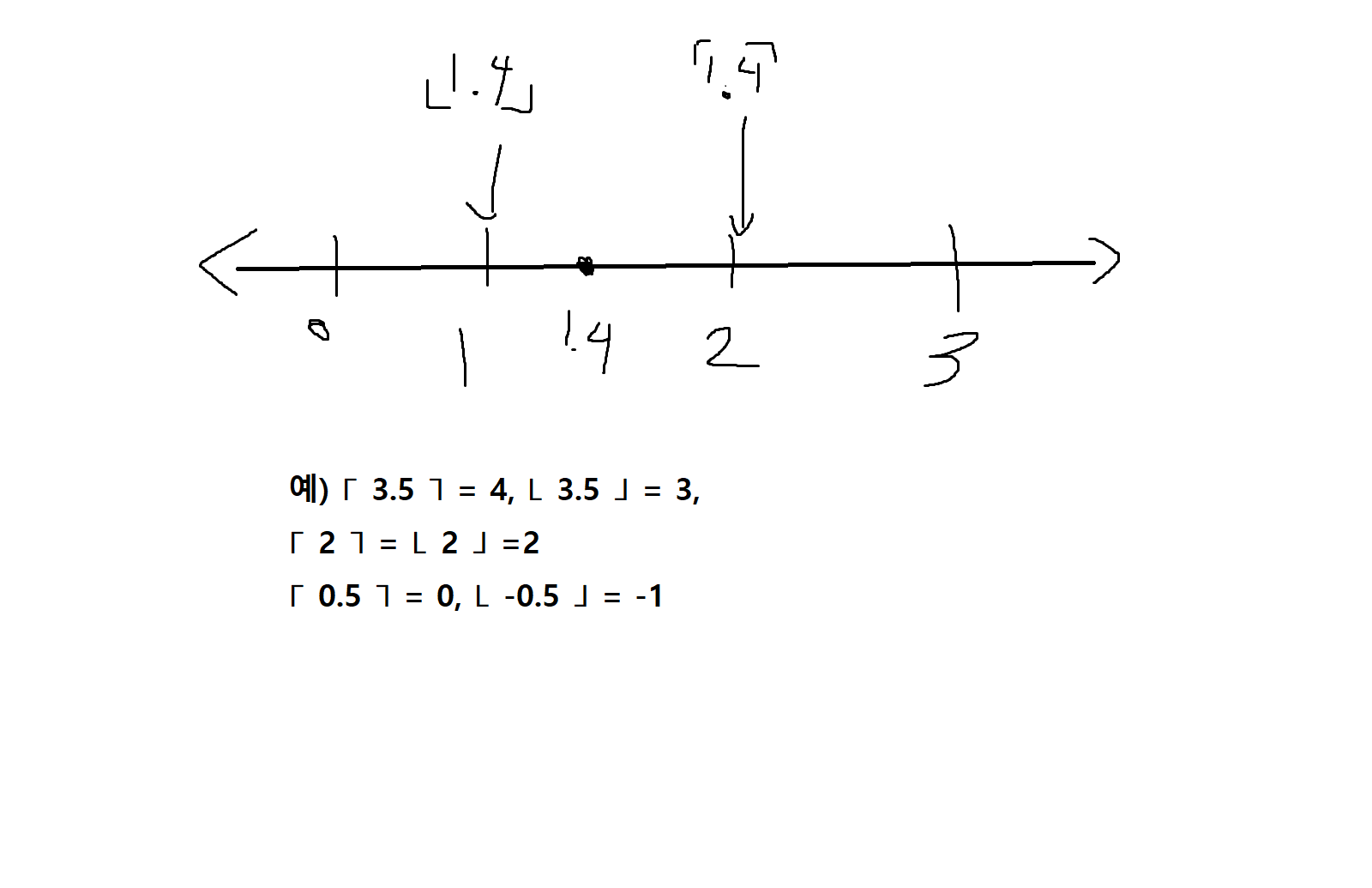
정의 6-11. x∈R에 대한 올림함수는 x보다 크거나 같은 정수값 중 가장 작은 값을 나타내며 ⌈ x ⌉로 표기한다. x∈R에 대한 내림함수는 x보다 작거나 같은 정수값 중 가장 큰 값을 나타내며 ⌊x⌋로 표기한다.
- 컴퓨터 프로그램을 작성하는데 있어서, 일반적으로 복잡한 문제를 여러 개의 독립적인 기능을 가지는 서브 프로그램(하나의 함수)으로 나누어서 해결함 -> 그래야 디버깅이나 모델링도 편함
- 서브 프로그램들은 각기 논리적으로 독립된 계산을 할 때나, 동일한 수행을 여러번 해야 할 때 많이 사용
- 예를 들면, 입력되는 데이터에 대하여 같은 일을 계속 수행해야 하는 경우에는 데이터마다 수행해야하는 부분을 서브프로그램으로 만들어서 필요한 경우 호출하여 사용
- 서브프로그램 중 함수에 속하는 서브프로그램은 정의역에 있는 매개변수의 값을 받아서 계산을 한 뒤 하나의 값을 되돌려 줌
- 함수호출 (function call) : 매개변수(parameter)를 가지고 함수를 부르는 것
- 리턴 (Return) : 함수에서 계산된 값을 되돌려 주는 것임
컴퓨터 언어에서의 두가지 함수
라이브러리 / 프로그래머가 작성한 함수
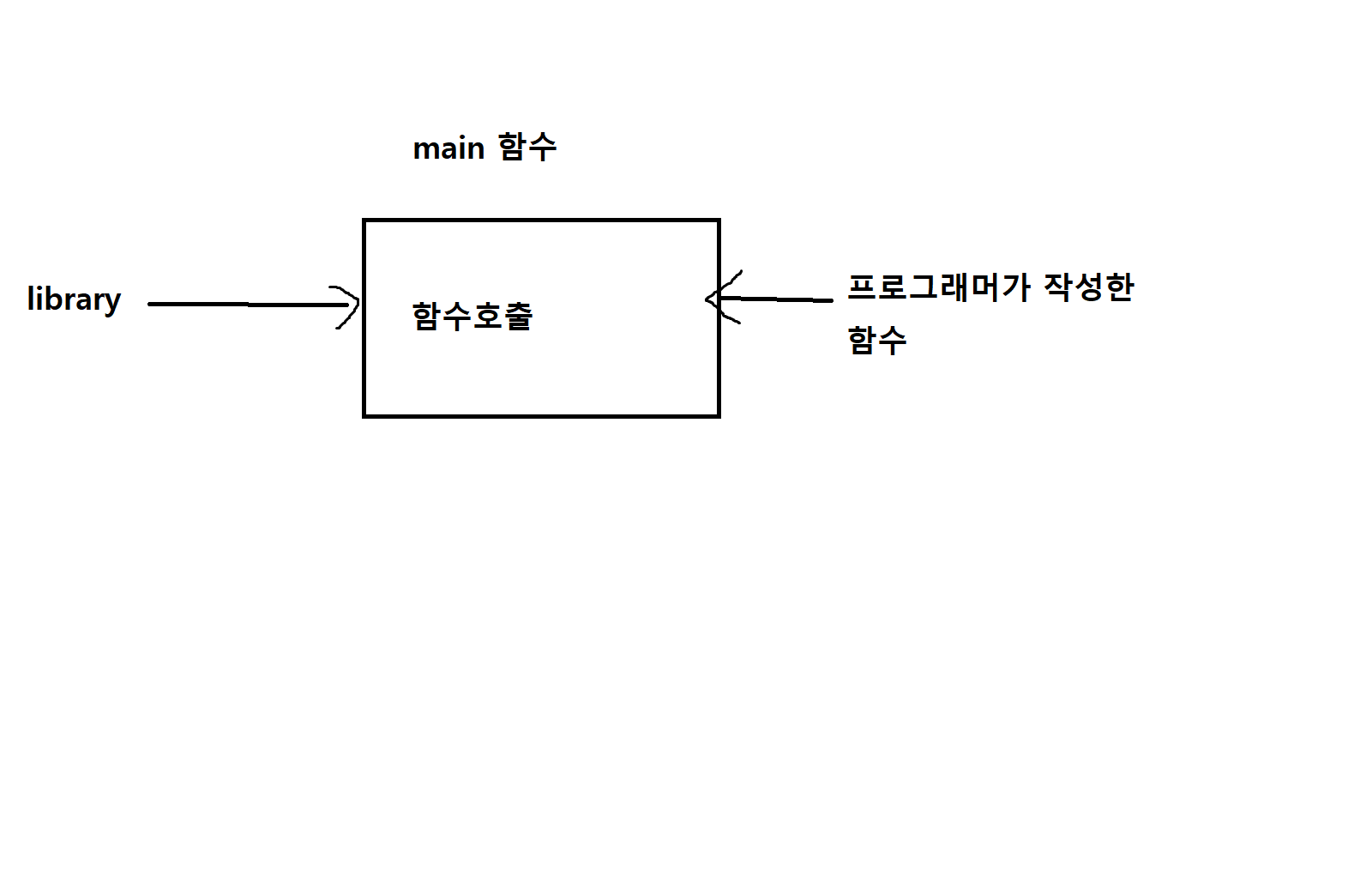
- 컴퓨터 언어에서의 함수들도 일반적인 함수의 기능과 같은 역할을 프로그램 내에서 수행함
- 컴퓨터 프로그램을 작성할 때 알맞은 함수를 사용하면 좀 더 명확하고 간단하게 문제를 해결할 수 있음
연습문제
1) 함수 f, g, h : Z -> Z, f(x) = x-1, g(x) = 3x,
h(x) = 0 (x가 짝수일때), = 1 (x가 홀수일때) 일 경우 다음을 구하시오.
가) f * g
3x - 1
나) g * h
0 (x가 짝수일때)
3 (x가 홀수일때)
2) 함수 f: {1,2,3} -> {a,b,c}이고 f(1)=b, f(2)=c, f(3)=a 일 경우 f의 역함수는 존재하는가? 존재한다면 역함수를 구하시오
전단사 함수일 때만 역함수가 존재한다)
3) 세 집합 A=B=C=R, f:A->B, g:B->C이며 f(a) = a²-2, g(b) = 2b+1 이라고 정의할 때 다음 합성함수를 구하시오.
가) g * f(-1)
g(-1) = -1
나) f * g(-1)
f(-1) = -1
다) (g * f) g(x)
= g(4b²+4b-1) = 8b²+8b-1
라) (g f) f(x)
= g f(f(x)) = g(a⁴-4a²+2) = 2a⁴-8a²+5
