이산수학(10)

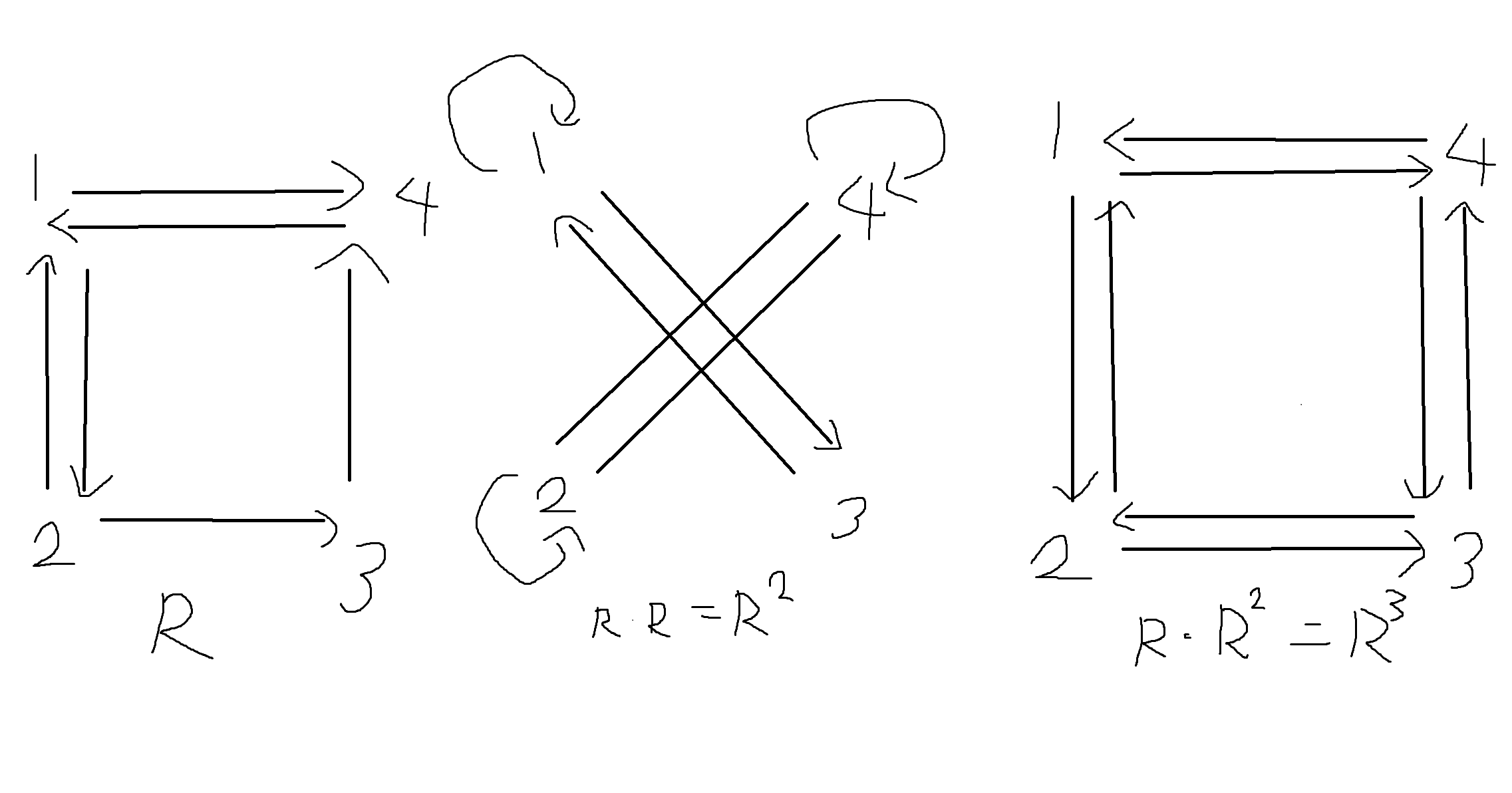
5.4. 관계의 성질 - 추이 관계

(6) 추이관계 (Transitive Relation)
-> 집합 A에 있는 원소 x,y,z에 대하여 관계 R이 (x,y) ∈ R이고, (y,z) ∈ R이면 (x,z) ∈ R인 관계를 만족할 때 관계 R을 추이관계라고 한다.

• A->B, B->C, A->C 이 관계

• 집합 A = {1,2,3}이고, R = {(1,2), (2,3), (1,3)}일 경우 관계 R은 추이 관계임

• 집합 A = {1,2,3}이고 S = {(1,3), (2,2), (3,2)}일 경우 관계 S의 순서쌍에 (1,3)과 (3,2)가 존재하나 (1,2)가 존재하지 않으므로 관계 S는 추이관계가 아님

• 집합 A = {1,2,3}이고 R = {(1,2)}일 경우 관계 R의 순서쌍은 (1,2)뿐이고 2로 시작하는 순서쌍이 존재하지 않으므로 관계 R은 추이 관계임.

예제 5-22. 정수들의 집합에서 크기를 나타내는 관계 <에서 추이관계가 성립함을 보여라.

3<5, 5<7, 3<7 (추이관계 성립함)

반사 - X
비반사 - O
대칭 - X
비대칭 - O
반대칭 - X

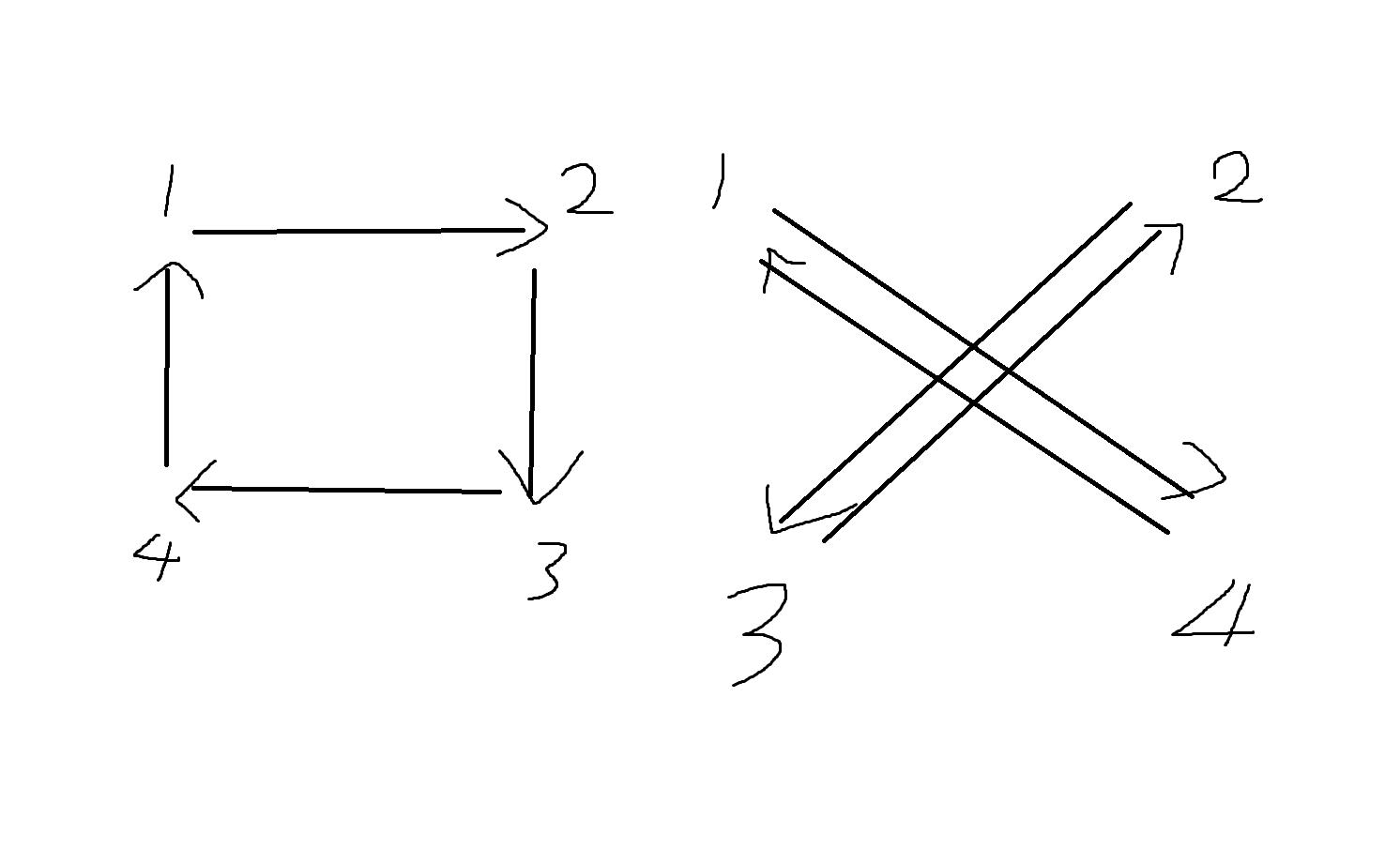
예제 5-23. 다음의 방향 그래프로 표현된 관계들이 추이관계인지를 판별해보자.

(1)
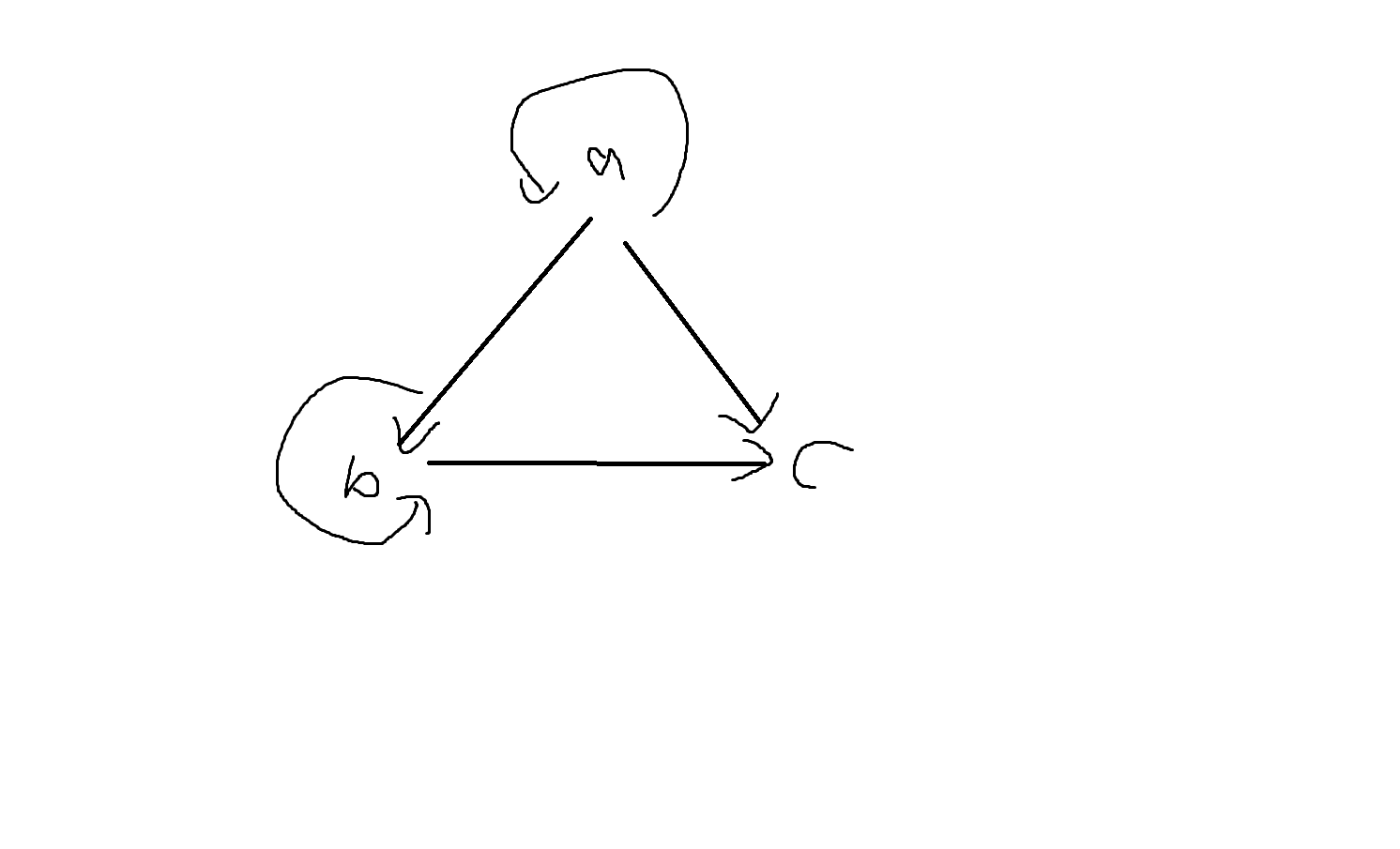
(a,b) ∈ R₁, (b,c) ∈ R₁일때 (a,c) ∈ R₁ -> 추이관계 성립합

(2)
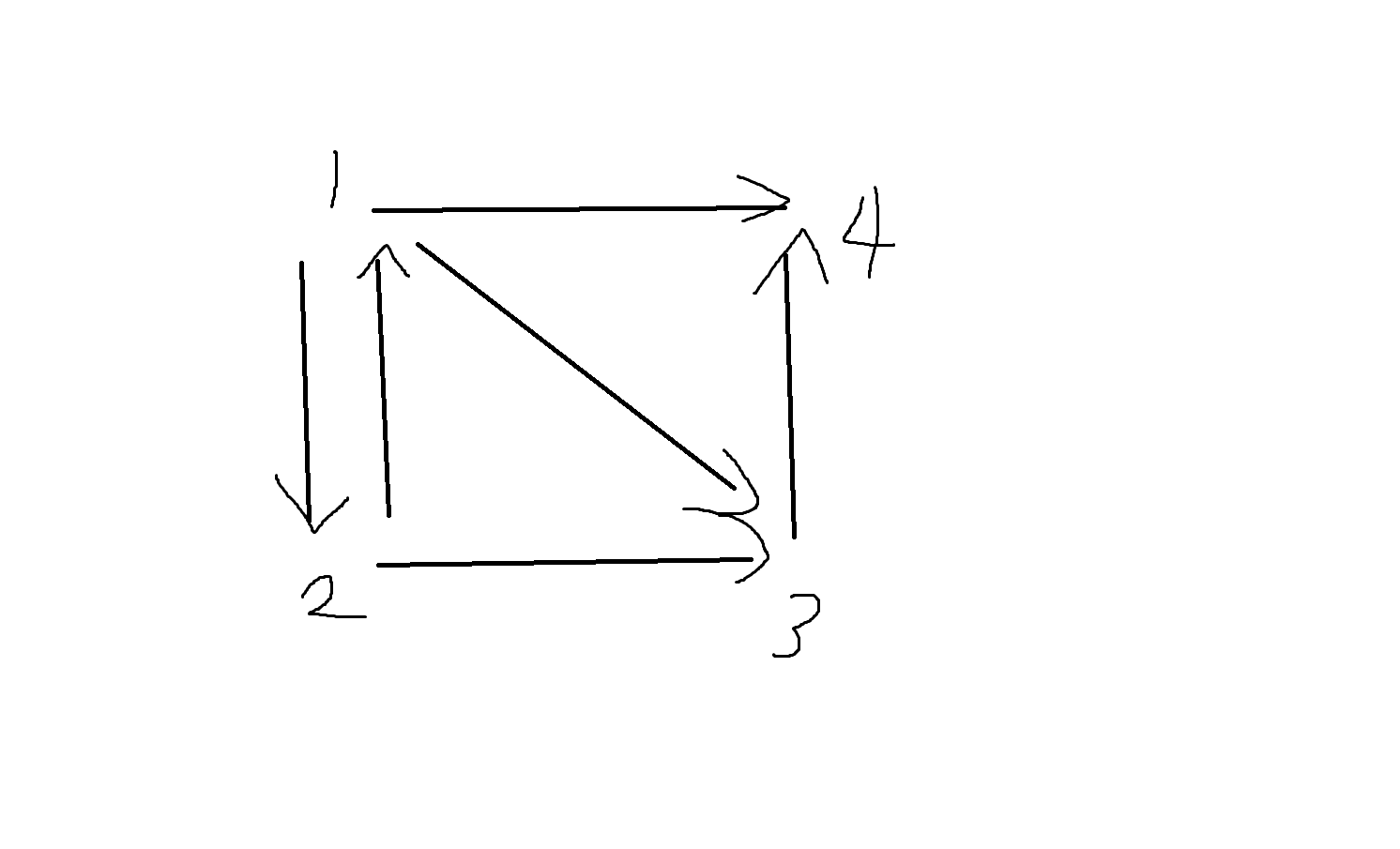
(1,2) ∈ R₂, (2,3) ∈ R₂일때 (1,3) ∈ R₂
하지만 (2,1) ∈ R₂, (1,4) ∈ R₂일때 (2,4) !∈ R₂이므로 R₂는 추이관계가 아님. (모든 관계에서 만족해야 추이관계가 성립함)

예제 5-24. A = {1,2,3,4}라 하고, A 상에 어떤 관계가 다음 행렬과 같이 주어졌다면 그 관계가 반사관계, 대칭관계, 반대칭관계, 추이관계가 성립하는지를 살펴보자.

A = {1,2,3,4}라 하고, A 상에 어떤 관계가 다음 행렬과 같이 주어졌다면 그 관계가 반사관계, 대칭관계, 반대칭관계, 추이관계가 성립하는지 살펴보라.

	1	2	3	4
1	1	1	0	0
2	1	1	0	0
3	0	0	1	0
4	0	0	0	1

반사 O
비반사 X
대칭 O (\ 대각선 기준 접었을 때 동일)
반대칭 X (1,2) (2,1)
추이 O (1,2) - (2,1) - (1,1) 나머지는 없음

예제 5-25. 어떤 집합상에 관계가 주어졌을 때, 그 관계에 따른 방향 그래프가 다음과 같다. 이때 반사관계, 대칭관계, 반대칭관계, 추이관계가 성립하는지 판별해보자.

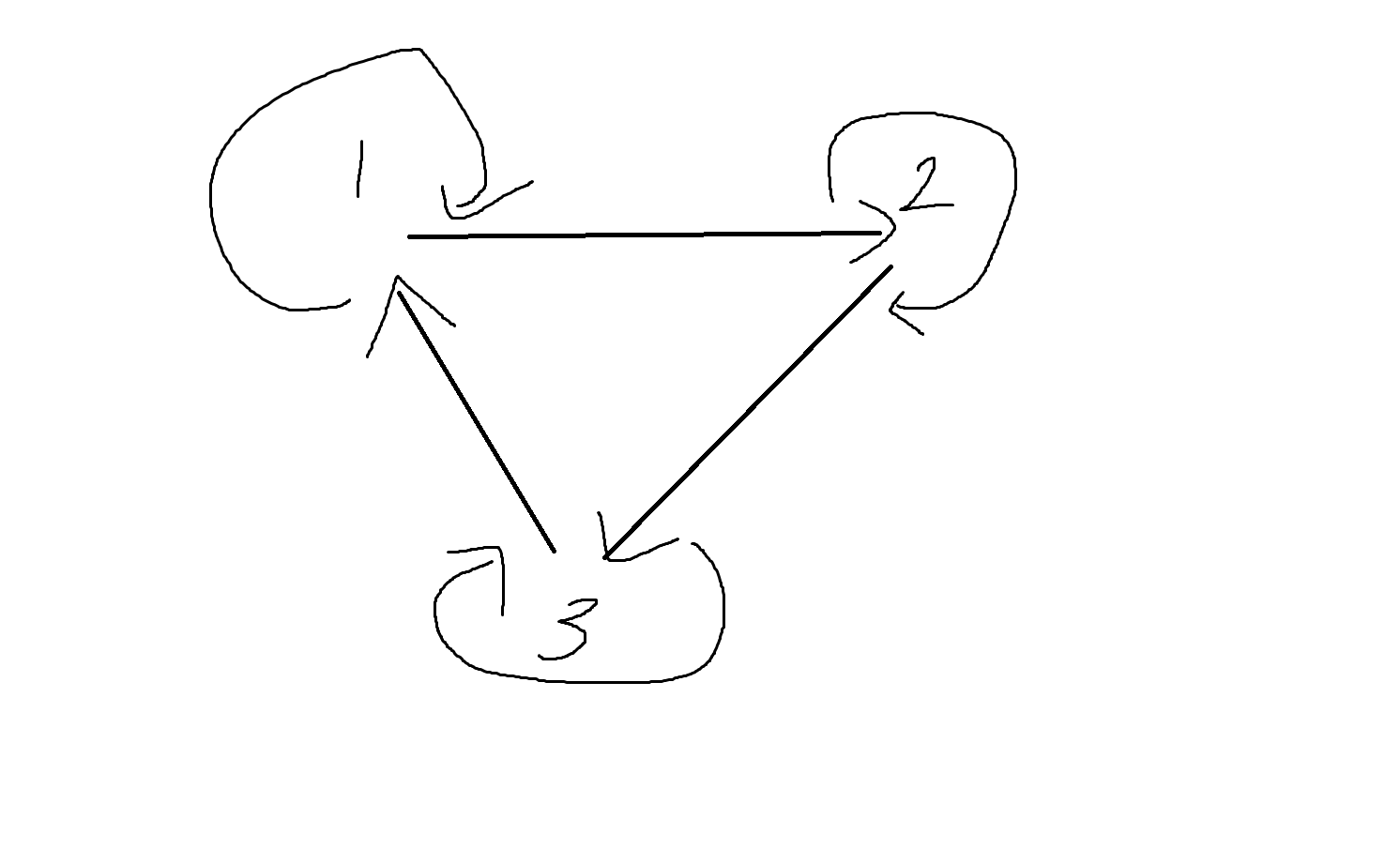
반사 O
대칭 X
반대칭 O
추이 X (1,2) - (2,3) - (1,3)없음

<정의 5-9-1> R^n

• 임의의 정점에서 경로의 길이가 n이 되는 정점들의 쌍
• n >= 1일때 R^n은 다음과 같이 정의

R^n = R (if n=1)
= R * R^(n-1) (if n>1)

R^4 = R R^3 = R R R^2 = R R R R

R^n을 구하는 방법

(1) 방향 그래프

• R²는 각 정점에서 길이가 2인 경로로 가는 정점을 찾아서 화살표를 가진 연결선으로 이어주면 된다.
  

(2) 관계 행렬

• R² = R * R

0100 0100 0001
0001 0001 0010
1000 1000 0100
0010 0010 1000

정의 5-10. R의 추이 클로우저 R^+ = R∪R²∪R³∪..... 는 다음과 같이 정의한다
(1) 만약, (a,b) ∈ R이면 (a,b) ∈ R^+이다.
(2) 만약, (a,b) ∈ R^+이고 (b,c)∈R이면 (a,c)∈R^+이다.
(3) 앞의 (1), (2)의 경우를 제외하고는 어떤 것도 R^+에 속하지 않는다.

R^+ : 임의의 정점에서 적어도 길이가 하나 이상인 경로로 도착할 수 있는 정점들의 쌍의 집합

R^+에서는 추이관계가 성립한다. R ^ *로 표현되는 R의 반사 및 추이 클로우저는 R^+ ∪ {(a,a)| a∈S}가 된다.

정리. 집합 A에서의 관계 R ⊂= A * A는 다음과 같은 성질을 가질 수 있다.

(1) 반사관계 : 모든 x∈A에 대해 xRx이다.
(2) 대칭관계 : 모든 x,y∈A에 대해 xRy이면 yRx이다.
(3) 추이관계 : 모든 x,y,z ∈ A에 대해 xRy이고 yRz이면 xRz이다.

예제 5-26. R = {(1,2), (2,2), (2,3)}을 집합 {1,2,3}상에서의 관계라고 할 때 R^+와 R^*을 구해보자.

만약 (a,b) ∈ R^+이고 (b,c) ∈ R이면 (a,c) ∈ R^+이다.
따라서 R^+ = {(1,2), (2,2), (2,3), (1,3)}이 된다.
한편 R^ = R^+ ∪ {(a,a)| a∈S} 이므로
R^ = {(1,1), (1,2), (1,3), (2,2), (2,3), (3,3)}이 된다.

• R^+는 추이관계 추가. R^*은 반사(자기자신으로의 관계) 추가

요약

• 집합 A에 있는 원소 x,y,z에 대하여 관계 R이 (x,y) ∈ R이고, (y,z) ∈ R이면 (x,z) ∈ R인 관계를 만족할 때 관계 R을 추이관계라 한다.

• R^+ : 임의의 정점에서 적어도 길이가 하나 이상인 경로로 도달할 수 있는 정점들의 쌍의 집합

• R+에서는 추이 관계가 성립한다. R^* 로 표현되는 R의 반사 및 추이 클로우저는 R^+ ∪ {(a,a)| a∈S}가 된다.

연습문제

1)

다음과 같이 주어진 관계들에 대하여 이 관계가 반사, 비반사, 대칭, 비대칭, 반대칭, 추이 관계가 되는지를 결정하시오.
{(1,2), (2,3), (3,2), (2,1), (1,3), (3,1), (4,4)}

반사 X
비반사 X (4,4) 존재
대칭 O
비대칭 X
반대칭 X (다른 경우에는 성립하면 안되는데 성립하므로)
추이 X (2,3) - (3,2) - 인데 (2,2)는 존재하지 않음. 추이 X

2)

집합 A = {1,2,3}상에 관계가 주었을 때, 그 관계에 따른 방향 그래프가 다음과 같다면 반사, 비반사, 대칭, 비대칭, 반대칭, 추이 관계가 성립하는지 판단하시오.

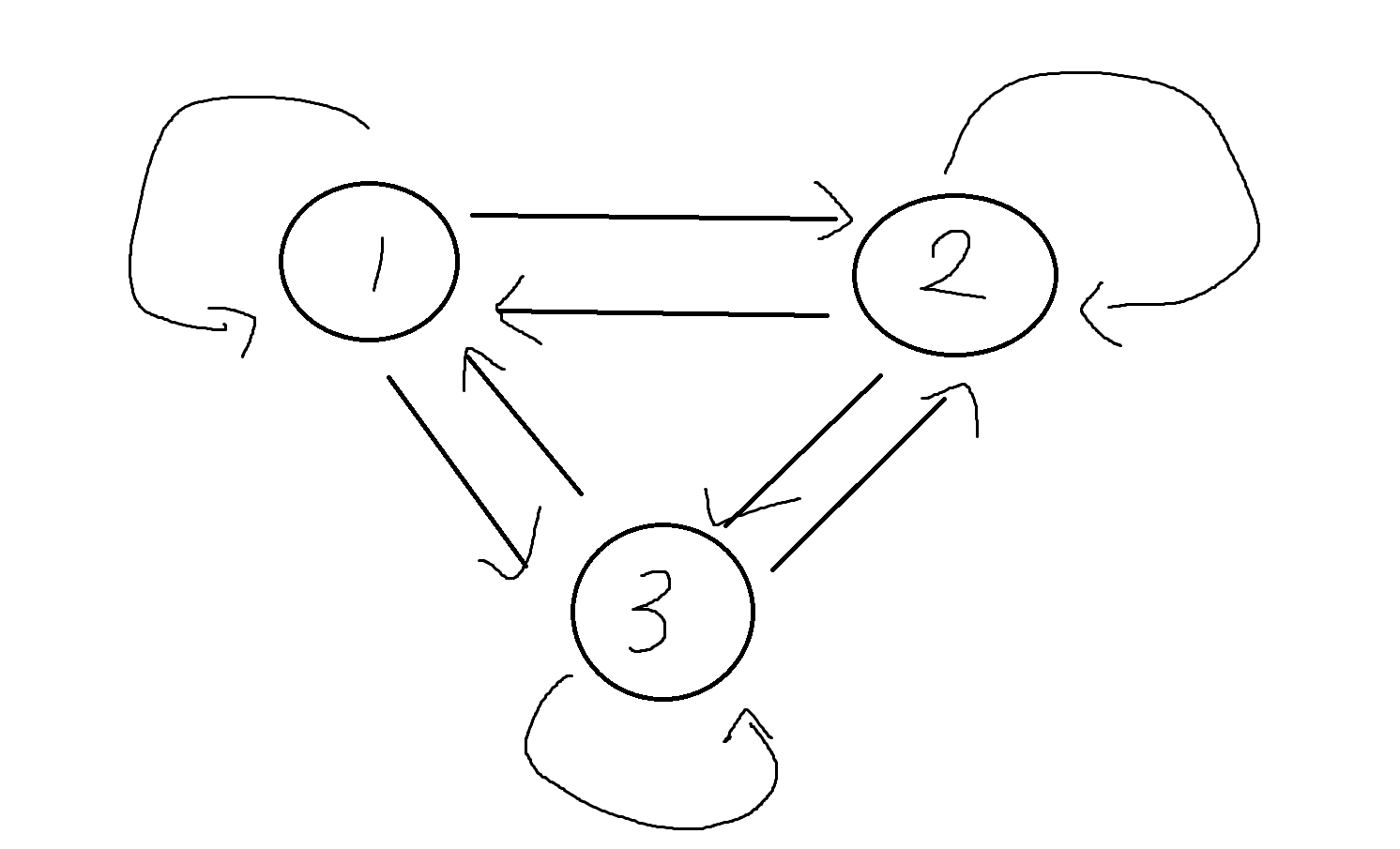
반사 O
비반사 X
대칭 O
비대칭 X
반대칭 X
추이 O

3)

집합 A = {1,2,3,4}에 대한 관계 R이 다음과 같이 주어졌을 때, R²와 R³를 방향그래프를 이용해 구하시오.
R = {(1,2), (1,4), (2,1), (2,3), (3,4), (4,1)}
(R² - 2번을 거쳐서 감, R³ - 3번을 거쳐서 감)