관계의 성질 (반사, 비반사, 대칭)
(1) 반사관계
-> 집합 A에 있는 모든 요소 x에 대하여 xRx이면, 즉 (x,x) ∈ R이면 관계 R은 반사관계라 한다.
-> 관계 R에 대한 방향그래프를 그렸을때, 그래프의 모든 정점에서 자기자신을 가리키는 화살표가 있어야 성립함
(다른 것과의 관계는 상관없고 자기자신으로 가는게 있으면 된다.)
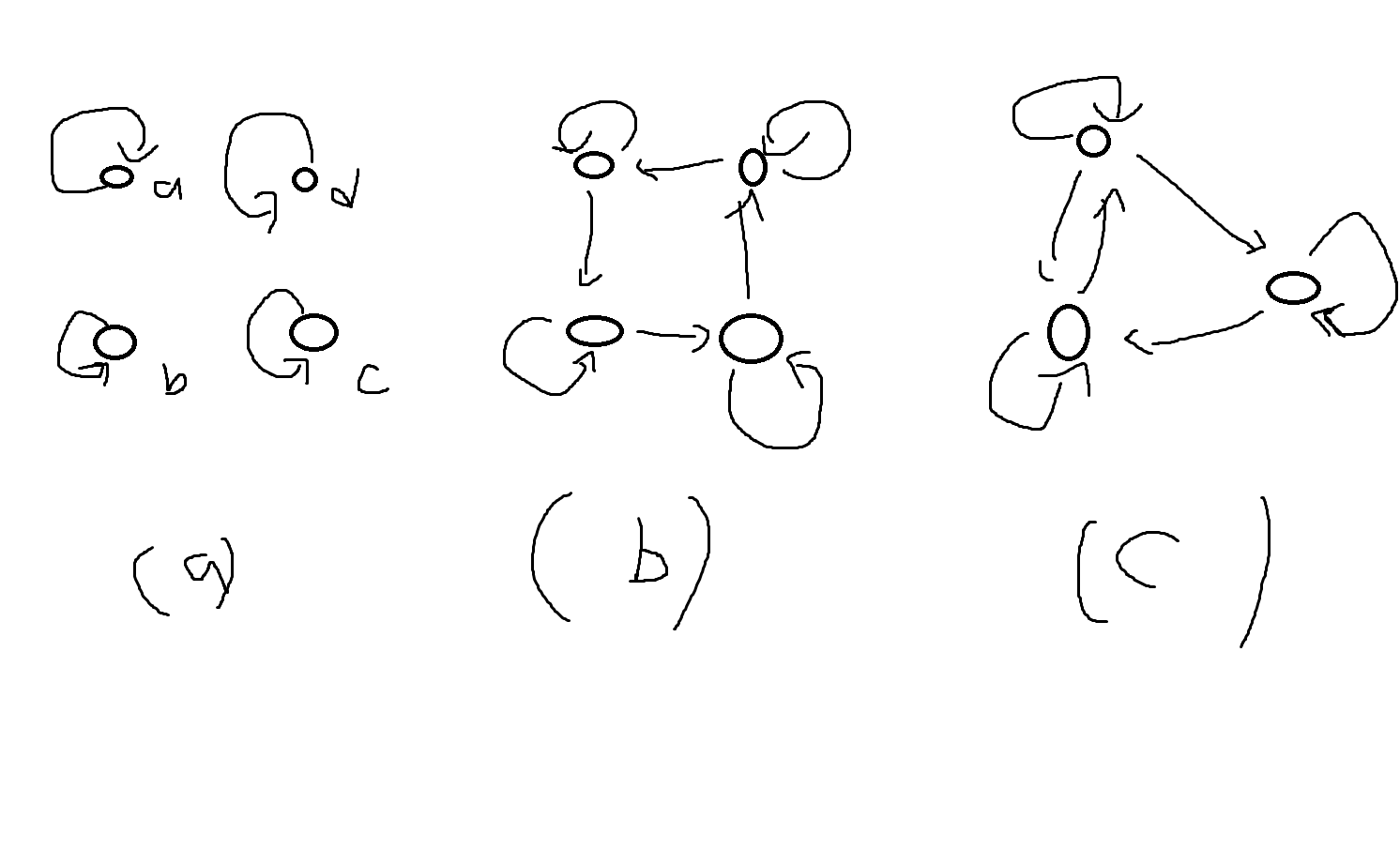
예제 5-18. 집합 A = {1,2,3,4} 다음 중 반사관계 인것?
R₁={(1,1),(1,2),(2,1),(2,2),(3,3),(3,4),(4,4)}
R₂={(2,2),(3,3),(4,4)}
R₃={(3,2),(3,3),(4,4),(4,1),(2,3),(1,1),(2,2),(1,3)}
R₄=∅
-> R1과 R3가 반사관계. R2,R4는 X
예제 5-19. R = {(a,b)|a∈N, b∈N, a<=b}일때 R이 반사관계인가?
-> 반사관계가 맞다. (a와 b가 같았을때 성립하므로)
(2) 비반사관계
- 반사관계와는 반대로 집합 A의 모든 원소에 대해 a∈A, (a,a)!∈R
- R이 비반사관계이면 R의 원소중에는 (a,a), a∈A인 원소가 하나도 존재하지 않음
(3) 대칭관계
- 집합 A에 있는 원소 x,y에 대해 (x,y)∈R일 때, (y,x)∈R이면 관계 R을 대칭관계라고 한다.
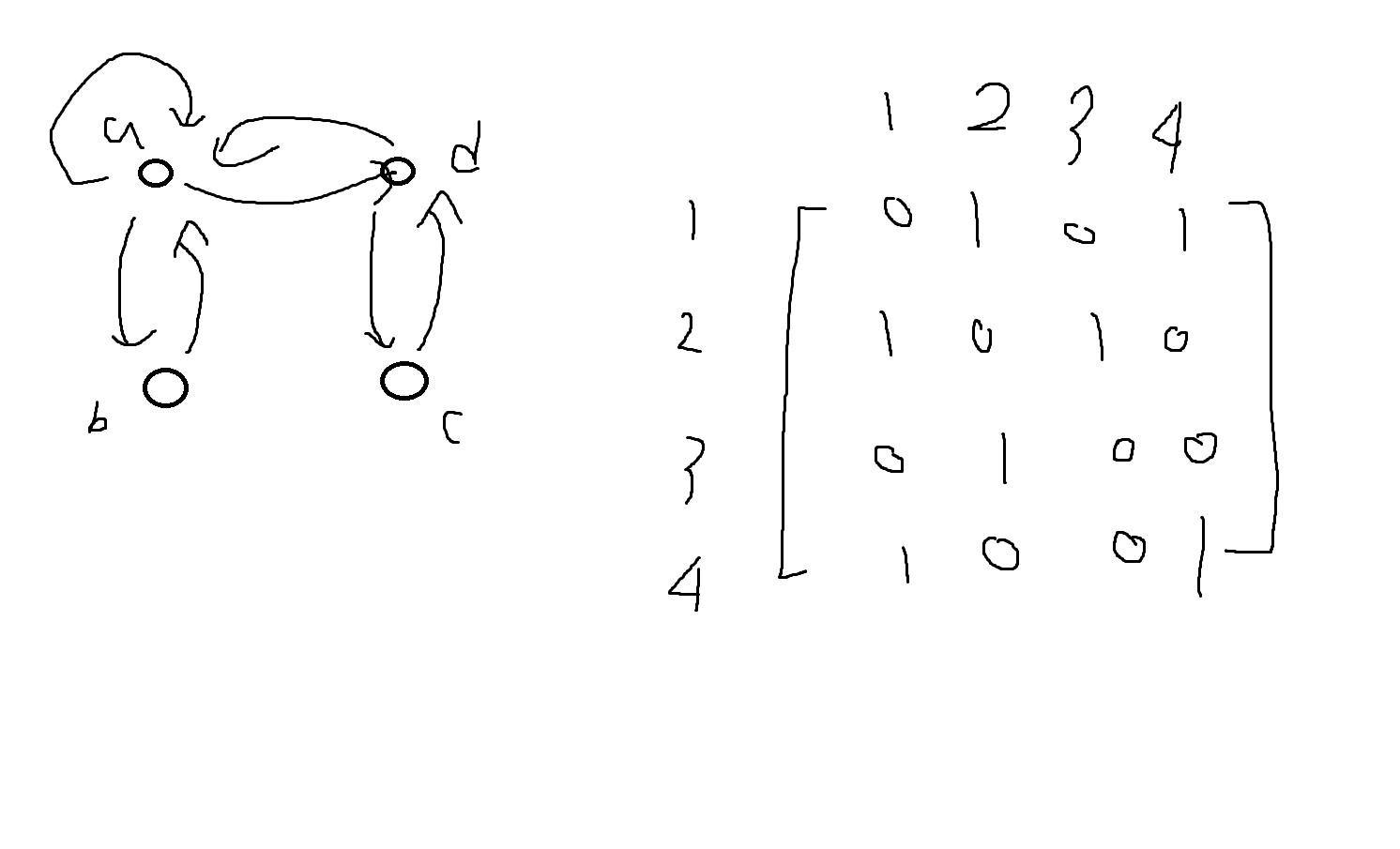
예제 5-20. x,y가 자연수의 집합 N의 원소일때, 다음의 관계들이 대칭관계인지 아닌지를 구별해보자.
(1) R₁ = {(x,y)|x∈N, y∈N, x+y=20}
대칭 O
(2) R₂ = {(x,y)|x∈N, y∈N, x<=y}
대칭 X
5<=10(참) -> 10<=5(거짓)
(4) 비대칭관계 (Asymmetric Relation)
- 집합 A에 있는 모든 원소 x,y에 대해 (x,y) ∈ R일 때, (y,x) !∈ R이면 관계 R을 비대칭이라고 한다.
(같은 것(a,a)이 있으면 비대칭)
(5) 반대칭관계 (반만 대칭)
-> 집합 A에 있는 모든 원소 x,y에 대하여 (x,y)∈R이고, (y,x)∈R일때, x=y인 관계를 만족하면 관계 R을 반대칭 관계라고 한다.
(3, 3) -> (3, 3) 반대칭 성립 O (x,y 같을 땐 성립)
(3, 2) -> (2, 3) 반대칭 성립 X (다를 땐 성립 X)
- R이 반대칭일때, x!=y이고 (x,y)∈R이면 (y,x) !∈ R
예제 5-21. 다음 관계들이 반대칭관계인지 아닌지를 구별해라.
(1) R₁= {(1,2), (2,2), (2,3), (3,1), (3,4), (4,4)}
같은 것에선 대칭 (4,4), (2,2)
다른 것에선 대칭 X (1,2), (2,3), (3,4), (3,1)
-> 반대칭 O
(2) R₂ = {(1,1), (1,3), (2,3), (3,1), (3,3), (4,1)}
(1,3), (3,1)에서 대칭이므로 반대칭에 해당하지 않는다.
(2-1) R₂의 반사, 비반사, 대칭, 비대칭, 반대칭 여부를 판별해라
반사 - X (2,3,4에서 자신에게 돌아오는 것이 없음)
비반사 - X (1,1)이 반례
대칭 - X (4,1)에 대한 대칭 (1,4)가 없음
비대칭 - X (1,1) / (1,3), (3,1)이 반례
반대칭 - X
요약
- 집합 A에 있는 모든 원소 x에 대하여 xRx이면, 즉 (x,x)∈R이면 관계 R을 반사관계라 한다.
- 반사관계와는 반대로 집합 A의 모든 원소에 대하여 a∈A, (a,a)!∈R이면 비반사관계라고 한다.
- 집합 A에 있는 원소 x,y에 대해 (x,y)∈R일때, (y,x)∈R이면 관계 R은 대칭관계라 하고, 집합 A에 있는 모든 원소 x,y에 대하여 (x,y)∈R이고 (y,x)∈R일떄, x=y인 관계를 만족하면 관계 R을 반대칭관계라 한다.
- 집합 A에 있는 모든 원소 x,y에 대하여 (x,y)∈R일때, (y,x)!∈R이면 관계 R을 비대칭관계라고 한다.
연습문제
1) A = {a,b,c}이고 관계 R₁과 R₂가 다음과 같을 때, 이 관계가 반사, 비반사, 대칭, 비대칭, 반대칭 관계인지를 구분하시오.
가) R₁= {(a,b), (a,c), (b,a), (c,a), (c,b)}
반사 X (자기 자신으로의 관계가 없음)
비반사 O
대칭 X (b,c)가 없음
비대칭 X (a,b), (b,a)가 반례
반대칭 X (a,b), (b,a)가 반례
나) R₂= {(a,b), (b,a), (b,b), (c,c)}
반사 X (a,a)가 필요
비반사 X (b,c)는 반사
대칭 O
비대칭 X
반대칭 X
2) 다음의 관계들이 반사, 비반사, 대칭, 비대칭, 반대칭 관계인지를 구분하시오.
가) R₁= {(1,2), (2,2), (2,3), (3,4), (4,1)}
반사 X
비반사 X
대칭 X
비대칭 X
반대칭 O
나) R₂= {(a,b) ∈ Z * Z, a <= b}
(a,b 둘 다 정수에 속한다)
반사 O (같은게 존재)
비반사 X
대칭 X (5<=10) (10 !<= 5)
비대칭 X (같은게 존재하니까)
반대칭 O (같은건 대칭이고 다른건 비대칭이고)
3) 집합 A = {a,b}이고 관계 R이 다음과 같을 때, 이 관계가 반사, 비반사, 대칭, 비대칭, 반대칭 관계인지 구해라.
R₁= {(a,a), (b,b)}
반사 O (자기 자신으로 돌아감)
비반사 X
대칭 O
비대칭 X
반대칭 O (a와 b사이의 관계가 아예 없으므로)
4) 집합 A = {a,b}이고 관계 R이 다음과 같을 때, 이 관계가 반사, 비반사, 대칭, 비대칭, 반대칭 관계인지를 구분하시오
R₂ = {(a,a), (b,b), (a,b)}
반사 O
비반사 X
대칭 X (a->b에 대한 대칭 b->a가 없음)
비대칭 X (a,a), (b,b)는 대칭이므로 비대칭 X (비대칭은 모든 관계에 대해 비대칭)
반대칭 O (같을땐 대칭, 다를땐 비대칭)
