집합론(1)
원소라 불리는 서로 다른 객체들의 모임으로 현대수학에서 가장 기초가 되는 개념 (중복된 원소는 없음)
- 집합은 정확하게 정의되어야 함
- 집합은 어떤 객체가 그 집합에 속하는지 아닌지를 분명하게 구분할 수 있어야 함
집합을 표현하는 방법
1) 원소 나열법
S = {1, 2, 3, 4, 5}
2) 조건 제시법
S = {x|P(x)}
-> x는 원소를 대표하는 변수, P(x)는 원소들이 가지고 있는 성질
예제 3-1)
원소나열법으로 나타내라
(1) {x|x∈N, x²=9} => {3}
(2) {y|y∈Z, 3<y<7} => {4,5,6}
조건제시법으로 나타내라
(1) 0부터 1사이 실수 집합
{x|x∈R, 0<=x<=1}
(2) 20보다 작은 홀수의 집합
{x|n은 정수이고, x=2n+1이고 n<10}
(3) x²=x를 만족시키는 정수의 집합
{x|x는 정수이고, x²=x}
카디날리티(Cardinality)
- 집합 S내에 있는 서로 다른 원소들의 개수
- 집합의 원소수라 하고 |S|로 표기함
- 집합 A={1,3,5,7,9} => |A| = 5개
예제 3-3. 유한, 무한집합을 판단하시오.
(1) 대한민국에 사는 모든 공대 학생들의 집합 -> 유한집합
(2) 5의 배수인 자연수의 집합 -> 무한집합
예제 3-4. 유한,무한집합을 판단하고 원소의 개수를 구하시오.
(1) {x|x∈Z, 2<x<5} -> 3,4 2개(유한집합)
(2) {x|-1<=x<=1, x는 유리수} -> 무한집합, 무한개
(3) {n|n∈N, n은 짝수| -> 무한집합, 무한개
- 집합 S₁에서 집합 S₂로의 일대일 대응인 함수가 존재할 때 S₁과 S₂가 같은 카디날리티를 가짐.
- 유한집합일 경우 만약 S₁이 S₂의 진부분집합 일때는 S₁과 S₂는 서로 다른 카디날리티를 가짐. (진부분집합 = 자기자신을 제외한 부분집합)
예제 3-5) 집합 {0,1,2}와 {a,b,c}는 같은 카디날리티를 가지고 있는가?
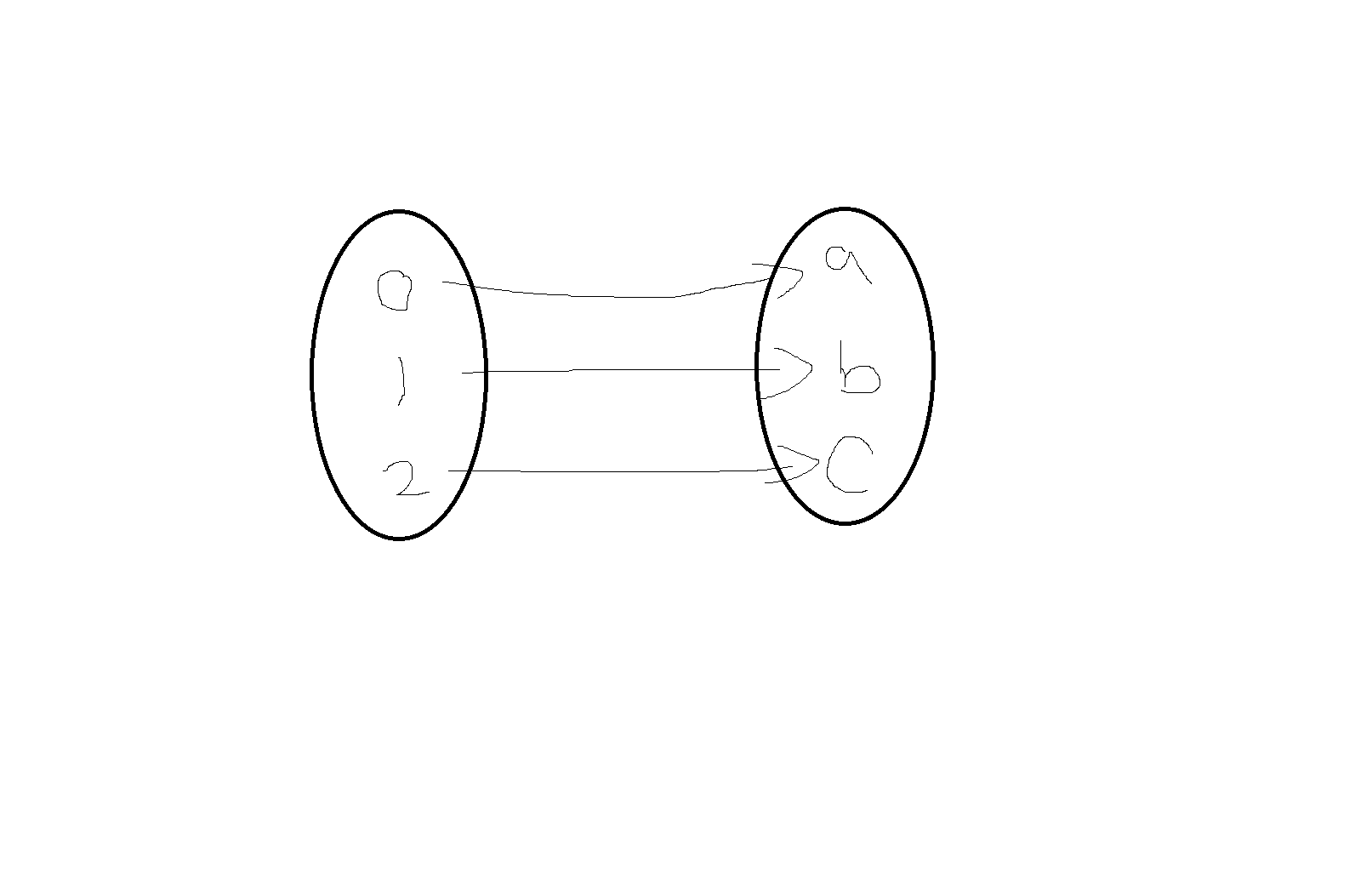
<그림3-2>에서 일대일 대응함수가 있으니 같은 카디날리티를 가진다.
예제 3-7) {x|x²-5=0, x는 정수}인 경우의 집합을 구해라
-> 해당하는 경우 없음. 공집합(∅)
예제 3-8
Z,N,R,Q -> 무한집합
Sn -> 유한집합
예제 3-9
(1) S = {x|x²=-2, x∈Z}
-> ∅
(2) R = {x|x∈N, x는 짝수 또는 홀수}
-> U (전체집합)
-
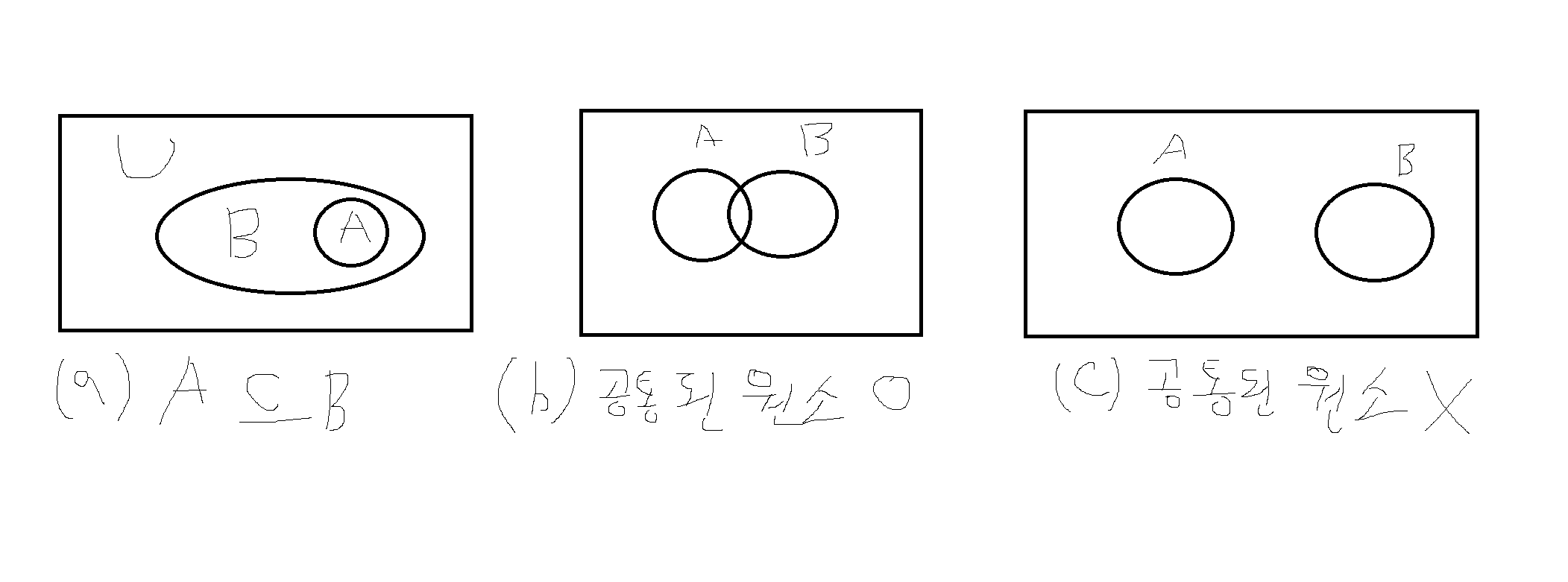
A⊂=B이고, A != B인 경우, A를 B의 진부분집합이라고 한다 (A⊂B로 표기)
(자기자신을 제외한 부분집합) -
여집합 = 자기자신을 제외한 부분에 해당하는 집합
정리. 집합 A, B, C, 전체 집합 U
(1) ∅ ⊂= A ⊂= U
(2) A ⊂= A
(3) (A ⊂= B ∩ B ⊂= C) => A ⊂= C
(4) (A⊂=B B⊂=A) => A=B
(5) ∅ ⊂= {∅}, ∅ ∈ {∅}
({∅}은 ∅을 원소로 갖는 부분집합. ∅하고는 다르다)
벤다이어그램
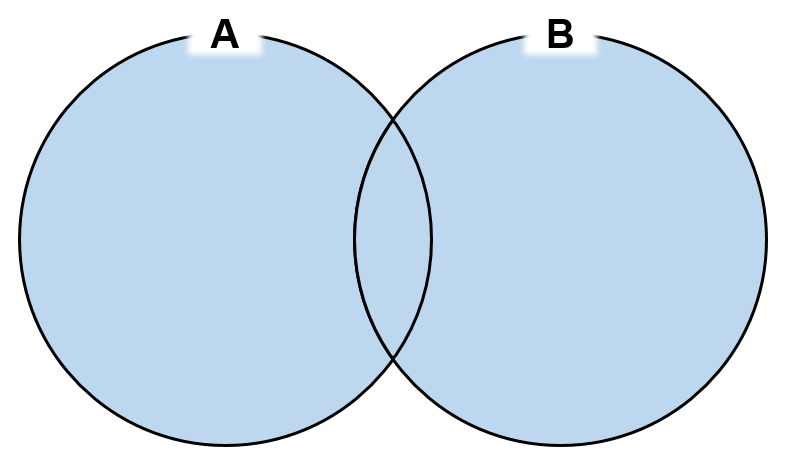
합집합
A∪B = {x|x∈A ∪ x∈B}
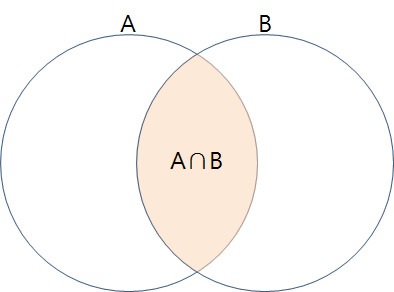
교집합(Intersection)
A∩B = {x|x∈A ∩ x∈B}
서로소(Disjoint)
-> 집합 A와 집합 B가 서로 교집합을 갖지않는 경우
차집합 (A-B)
A-B = {x|x∈A ∩ x !∈ B}
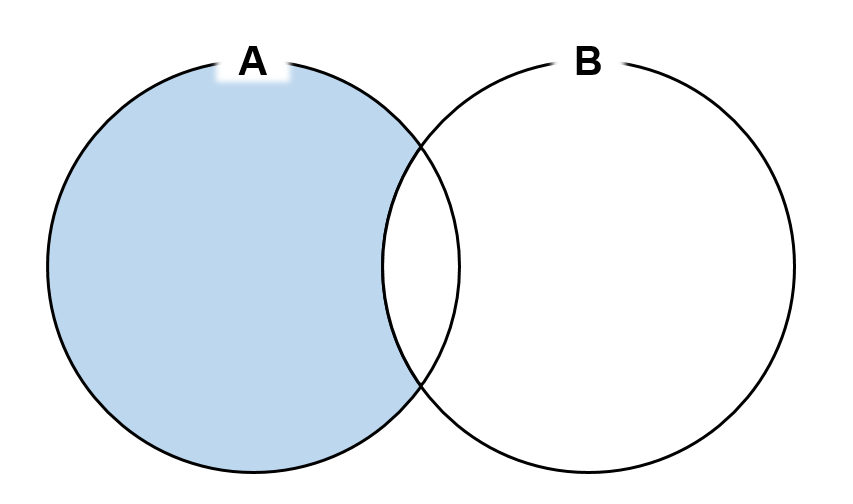
예제) A = {1,2,3,4,5}, B = {1,3,5}
A-B = {2, 4}
B-A = ∅
대칭차집합 : A⊕B (Exclusive Or)
집합 A,B에 대해 이들의 대칭차집합은 A∪B의 원소 중에서 A∩B에 속하지 않는 모든 원소들의 집합
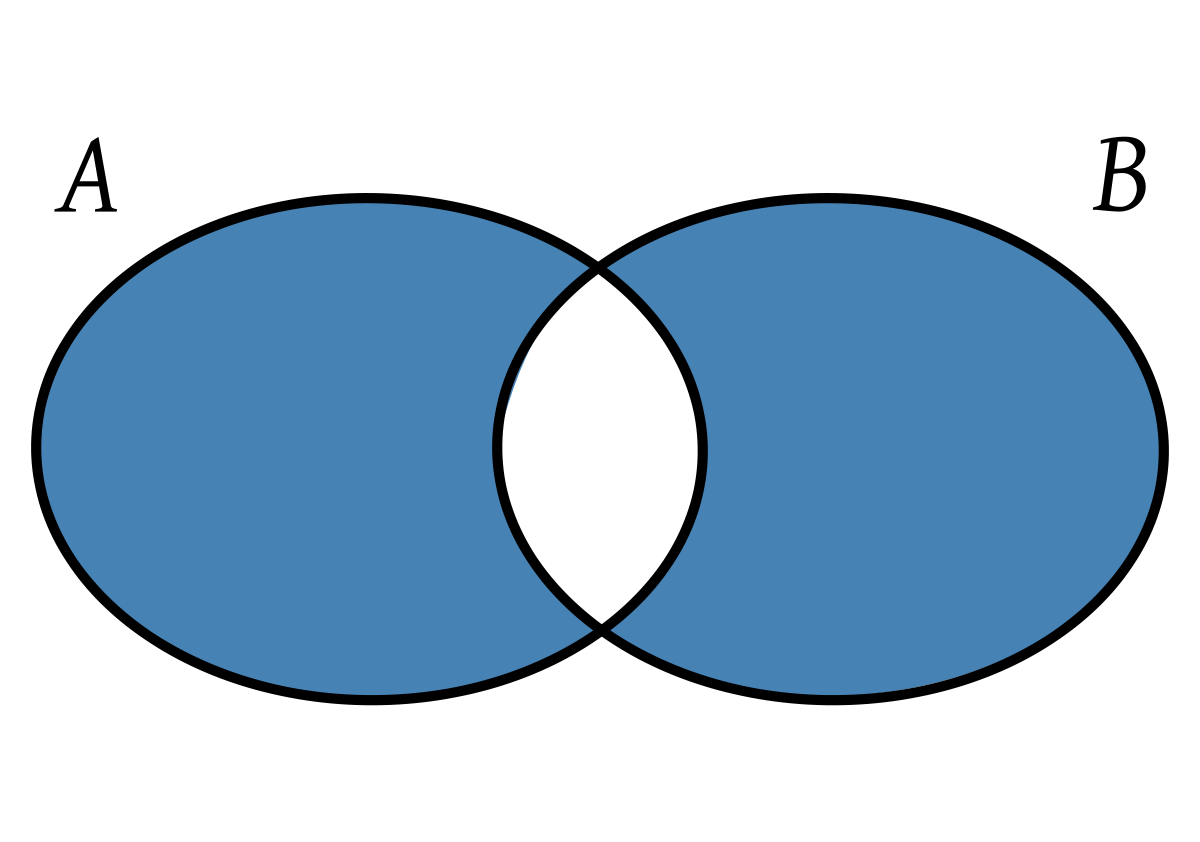
예제 3-16. A = {1,2,3,4,5}이고 B = {1,3,5,7,9}일때, A⊕B를 구해보라.
{2,4,7,9}
곱집합(Cartesian Product): A*B
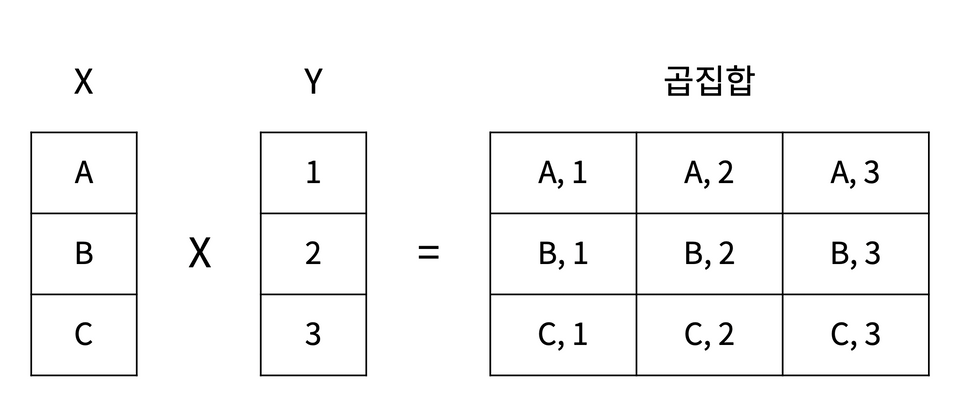
예제 3-17) A={1,2,3}, B={a,b,c}일때 A*B를 구해라.
{(1,a), (1,b), (1,c), (2,a), (2,b), (2,c), (3,a), (3,b), (3,c)}
예제 3-18) S={1,2,3,4)이고 T={2,4}일때
(1) ST에서 순서쌍의 개수? -> 42 = 8개
(2) {(x,y)|(x,y)∈S*T, x<y}의 원소를 나열해라
{(1,2), (1,4), (2,4), (3,4)}
연습문제
1) 조건제시법으로 나타난 집합을 원소나열법으로 나타내라
가) {x|x∈R, x²<0} -> ∅
나) {n|n∈N, n은 소수, n<15} -> {2,3,5,7,11,13}
2) 유/무한집합 판별
가) C언어에서 예약어들의 집합 -> 유한
나) x+y=1을 만족시키는 실수 x,y의 순서쌍 집합 -> 무한
3) A={1,2}, B={1,3}, A*B의 원소?
{(1,1), (1,3), (2,1), (2,3)}
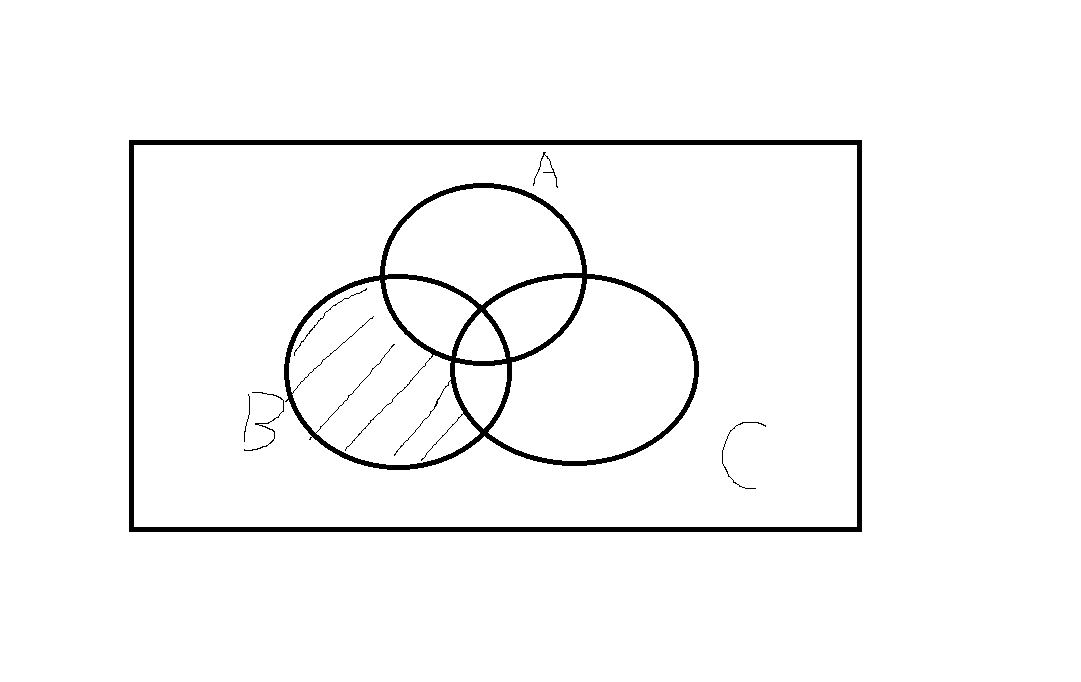
4) 집합 A,B,C에 대한 다음 연산을 벤다이어그램으로 나타내라
(A여집합 ∩ B) - C