집합론(2)
집합연산의 카디널리티(원소의 개수)
a. |A∪B| = |A|+|B|-|A∩B|
b. |A∩B| = |A|+|B|-|A∪B|
c. |A∪B∪C| = |A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C|
d. |A-B| = |A∩B의 여집합| = |A| - |A∩B|
e. |A B| =|A| |B|
예제 3-19. 어느 공대에서 이산수학과 C언어 프로그래밍 중 적어도 한 과목을 수강하는 학생이 80명이다. 만약 이산수학을 수강하는 학생이 55명이고, C언어를 수강하는 학생이 48명이면, 이산수학만 수강하는 학생 수는?
이산수학 - A, C언어 - B
A∪B = 80 = 55 + 48 - A∩B
A∩B = 23
A - A∩B = 55 - 23 = 32명
집합의 대수 법칙
1) 멱등법칙
A∪A = A
A∩A = A
2) 항등법칙
A∪∅ = A, A∩∅ = ∅
A∪U = U, A∩U = A
3) 교환법칙
A∪B = B∪A
A∩B = B∩A
4) 결합법칙
(A∪B)∪C = A∪(B∪C)
5) 분배법칙
A∪(B∩C) = (A∪B)∩(A∪C)
6) 흡수법칙
(A∩B)∪A = A
(A∪B)∩A = A
7) 보법칙
A의 여집합 = A
8) 역법칙
A∪A의 여집합 = U, A∩A의 여집합 = ∅
U의 여집합 = ∅, ∅의 여집합 = U
9) 드모르간 법칙
(A∪B)의 여집합 = A의 여집합 ∩ B의 여집합
(A∩B)의 여집합 = A의 여집합 ∪ B의 여집합
10) 기타법칙
A-B = A∩B의 여집합
A-A = ∅
A-∅ = A
- 쌍대(duality)
교집합과 합집합을 바꿈, 전체 집합(U)와 공집합(∅)를 바꿈
집합류(Class)
- 집합의 집단
- 집합 A에 대한 원소의 개수가 n이면 A의 부분집합의 개수는 2ⁿ개로 표현함
- 집합 A의 카디널리티로 표현하면 2의 |A|제곱
예제 3-24. S={a,b,c}, S의 멱집합?
{∅, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}}
2³=8
예제 3-25. A={a,b,{a}}라 할때 집합 A의 멱집합 P(A)?
-> 멱집합 = 모든 부분집합의 집합
P(A) = {∅, {a}, {b}, {{a}}, {a,b}, {a,{a}}, {b,{a}}, {a,b,{a}}
예제 3-26. A₁={1,2,3}, A₂={1,2,3,4,5}, A₃={1,2,3,5,7}, A₄={1,2,4,6,8}
A₁~ A₄의 교집합 = {1,2}
A₁~ A₄의 합집합 = {1,2,3,4,5,6,7,8}
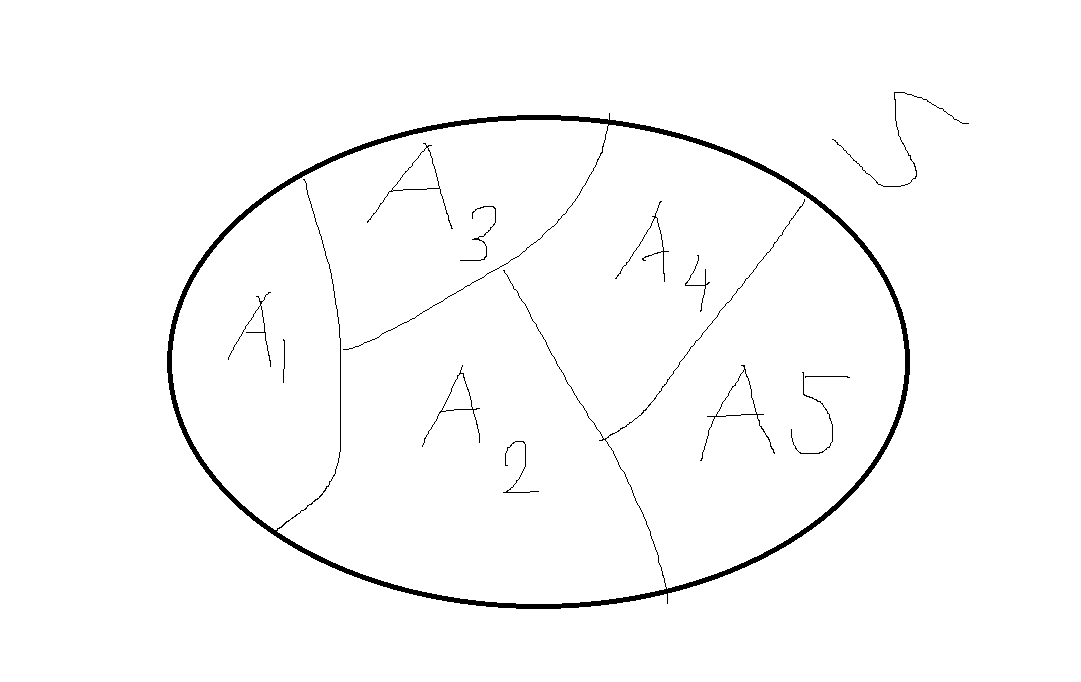
분할
분할의 원소인 A를 분할함
- 분할에 대한 예로 대한민국의 여러 도를 들수있음
- 각 도들은 공유하는 면적이 없고, 각 도를 합한 것은 대한민국 전체가 되므로 대한민국의 분할이라고 함
예제 3-27. 자연수 집합 N을 짝수와 홀수의 블록으로 분할해라
A1 -> 짝수
A2 -> 홀수
π = {A1, A2}
A1 = {x|n∈N, x=2n}
A2 = {x|x∈N, x=2n-1}
예제 3-28. A={1,2,...,8}, A1={1,3}, A2={2,6,7}, A3={4}, A4={5,8} 일때 π={A1, a2, a3, a4} A의 분할임을 보여라
-> 분할의 조건
1) ∅인 부분이 없고
2) 교집합이 없고
3) 다 합하면 U(전체)
A1~A4 중 ∅인 부분이 없고, 교집합이 없으며, 다 합하면 A와 같으므로 분할이 맞다.
1) 집합론에서 무한 개념으로 확장
2) 무한집합의 컴퓨터 모델 이론에의 기여
요약
-
합집합 : A∪B, 교집합 : A∩B, 차집합 : A-B, 대칭차집합:
-
공집합(카타시안 곱) : A * B 등이 있으며 벤다이어그램을 이용하면 보다 편리하다.
-
카타시안 곱은 다음과 같이 정의된다.
A B = {(x,y)|x∈A 그리고 y∈B}
이것을 일반적으로 확장하면 S1 S2 ... Sn = {(x1, x2,..., xn)|Xi∈Si}가 된다. -
집합에서 많이 이용되는 드모르간의 법칙은 다음과 같다.
(A∪B)의 여집합 = A의 여집합 ∩ B의 여집합
(A∩B)의 여집합 = A의 여집합 ∪ B의 여집합 -
멱집합 -> 집합 S의 부분집합을 원소로 갖는 집합
연습문제
1) 학생 80명이 수학과 영어 중 적어도 한 과목을 수강신청.
수학 52명, 영어 45명, 이때 수학만 신청한 학생수는?
A∩B = 52+45-80 = 17
52 - 17 = 35명
2) 멱집합 P({a,b})를 구해라
{∅, {a}, {b}, {a,b}}
3) 집합 S={1,2,3}의 모든 분할을 구하시오
1. {{1,2,3}}
2. {{1},{2,3}}
3. {{2},{1,3}}
4. {{3},{1,2}}
5. {{1},{2},{3}}
4) S={1,2,3,4,5,6}의 부분집합이 다음과 같을 때 분할에 해당하나?
{{1,2},{3,4},{5}}
1. 중복되는 것 없음
2. 적어도 하나의 원소
3. 합해서 전체
-> 다 성립하므로 분할이 맞다.
