확률변수 프로그래밍
replit
MatLAB -> 무거운 -> 온라인으로 쓰는게 빠름
-> 데이터 시각화에 유리함
컴퓨터에서 난수 생성
컴퓨터(Computer)?
-
회로의 전기적 신호의 유무 (ON / OFF)로 데이터 처리 (계산)
-
입력(Input)에 대한 출력(Output)을 계산
-
일반적인 컴퓨터는 기본적으로 난수(random number)를 만들 수 없다.
-
의사 난수 (Pseudorandom number, PRN)
-> 컴퓨터에서는 실제 난수가 아니라 난수와 매우 유사한 수열(Sequence)을 생성
-> 의사난수생성기 (PRN generator, PRNG): 여러 알고리즘이 존재 -
의사 난수 생성 알고리즘 (PRN generator, PRNG)
대표적 예시
- 선형합동법 (Linear Congruential method)
- Xn+1 = (aXn + c) mod m -> X0은 PRN의 초기값 (PRNG's seed)
- 사용언어 : C (a = 1103515245, c = 12345, m = 2^31) -> a, c, m 값 변경
-
중앙제공법
-
메르센 트위스터
균등 분포의 보편성 (1/3)
-
연속확률변수 X와 X의 CDF Fx(x)에 대해서, Y = G(x) = Fx(x)
확률변수 Y는 항상 0과 1 사이의 균등분포 (uniform distribution)가 된다. -
확률적분변환 (Probability integral transform)으로 불림
-
주의 : 확률변수 Y는 X의 함수변환 -> y = G(x) = Fx(x)
-
증명 : Fy(y) = Pr[Y <= y] = Pr[Fx(x) <= y] = Pr[X <= Fx^(-1)(y)] = Fx(Fx^(-1)(y)) = y
-> y의 범위는 0과 1사이 Pr[Y<=y] = y는 균등분포를 의미
연속확률변수 X의 분포를 따르는 난수 생성
- X = Fx^(-1)(Y) 관계 이용 (단, Y는 0과 1사이의 균등분포) (역함수)
(1) 0과 1사이에서 균등하게 분포하는 난수생성 -> yn
(2) xn = Fx^(-1)(yn) -> xn은 X의 분포를 따른다.
-> yn = Fx(xn) -> (역함수 관계)
(실습 #2) 특정확률분포를 따르는 난수생성
- X : 레일리 분포 (Rayleigh distribution)의 CDF와 PDF
Fx(x) = 1 - exp(-x²/2)
fx(x) = x * exp(-x²/2), 0 <= x < ∞
생각해볼 점
-
(손으로 직접) CDF의 역함수 구하기
-
(C언어) 난수생성 -> rand 함수 사용
-
(MATLAB) 생성되는 난수의 전체 수에 따른 분포모양 확인 (n = 100, 10000)
-
(MATLAB) 이론값의 PDF, CDF와 비교
-
(결과확인) 4개의 그래프 (PDF 2개, CDF 2개) -> 모든 그래프의 x축 범위 : [0, 5]

가우스 확률분포를 따르는 난수생성
-
(복습) 가우스 (정규)확률변수의 CDF (확률변수 : X, 평균 : µ, 분산 : σ²)
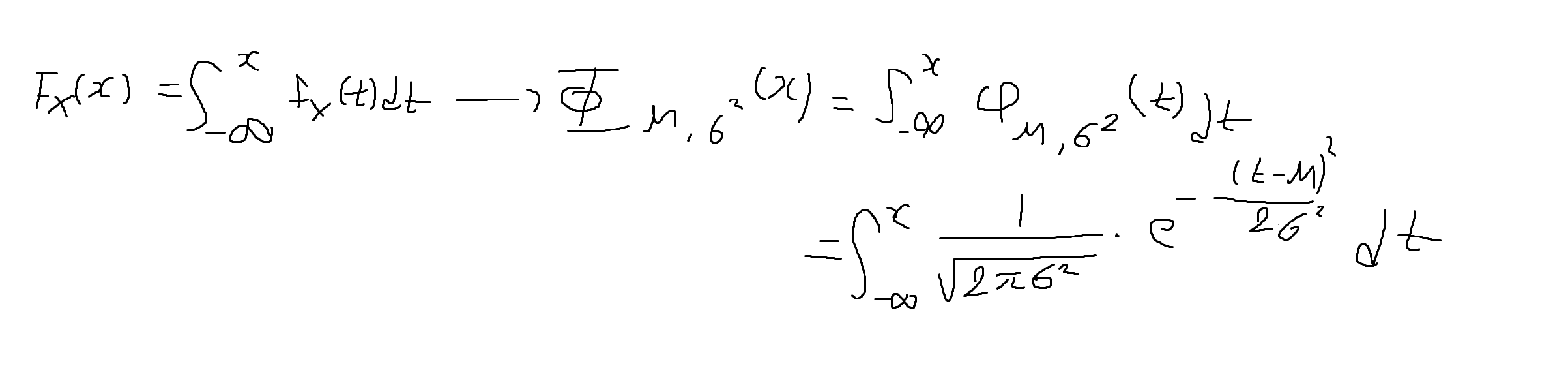
-
다양한 평균(µ) / 분산(σ²) 조건 -> 표준정규분포 z 변환해서 생각
-
X에서 변환 : z = (X - µ) / σ
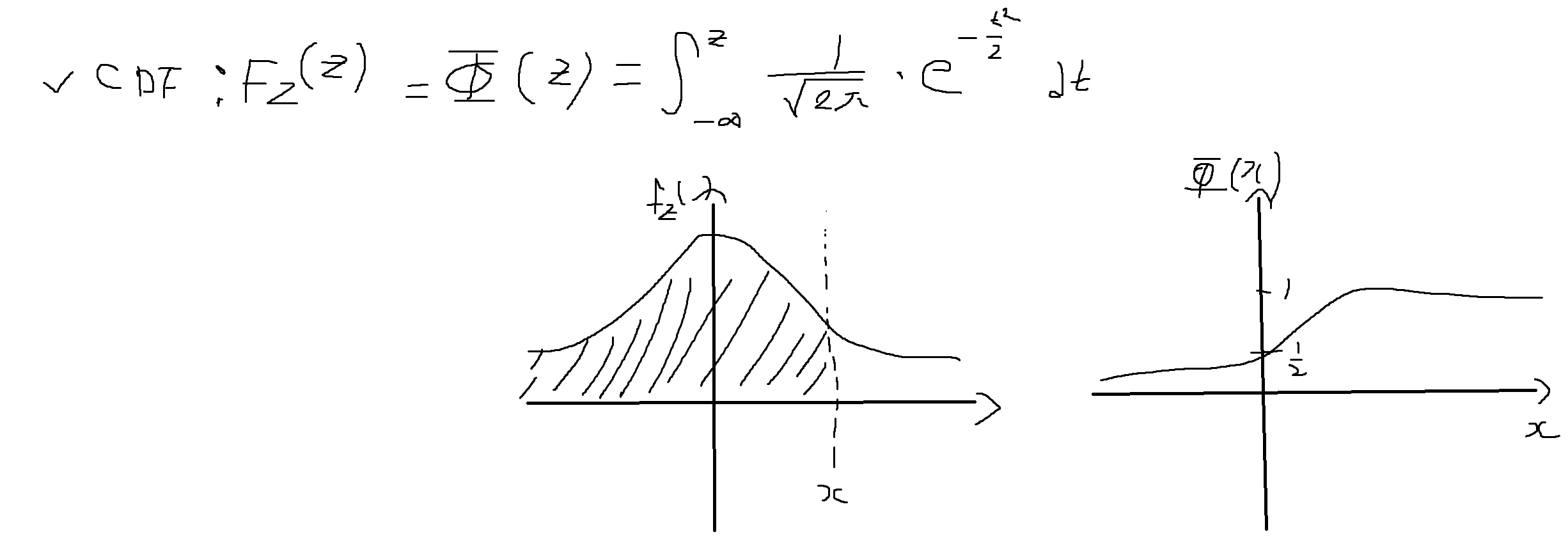
표준정규분포 z를 따르는 난수생성 방법
(방법 1) 균등분포의 보편성 이용
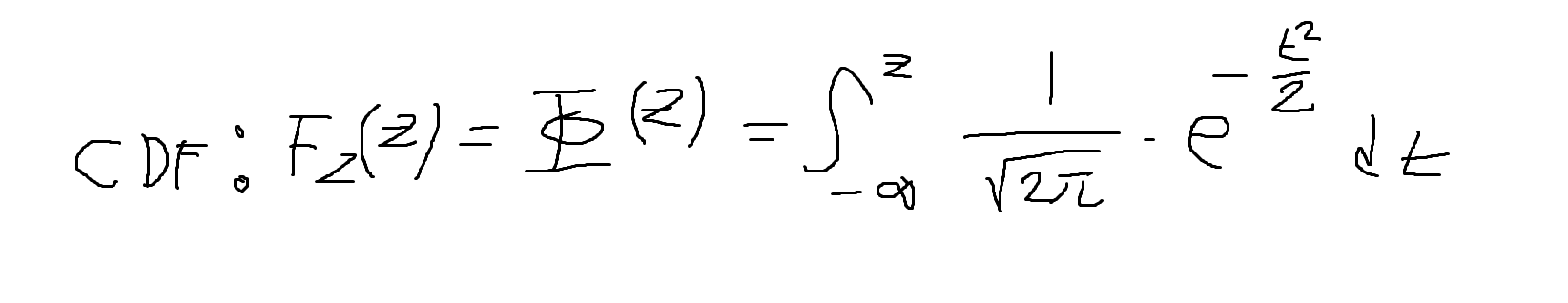
-
U : 표준(0과 1사이) 균등확률변수 -> uk 특정샘플(난수) 생성
-
zk = Fz^(-1)(uk) 생성 -> 생성된 샘플(난수) zk는 Z의 분포를 따른다.
-
주의! z의 CDF의 역함수 (Fz^(-1)(z))을 구하는 것이 어렵다.
-> 그럼 어떻게? CDF또는 CDF의 역함수의 근사(approximation) 함수를 이용
(방법 2) Box_Muller 방법
-
두 확률변수의 함수 변환 -> z = g(u, v)
-> z가 표준정규분포가 되는 g(u, v)? -
u, v : 서로 독립인 표준균등확률변수 -> uk, vk 특정샘플 생성

가우스 확률변수 쌍과 상관계수
(복습) 결합가우스 확률변수
-
X~N(µx, σ²x), Y~N(µy, σ²y)가 각각 가우스 확률변수
-
ρx,y : 두 확률변수의 상관계수
-
(X, Y)의 결합확률밀도함수 (joint PDF)
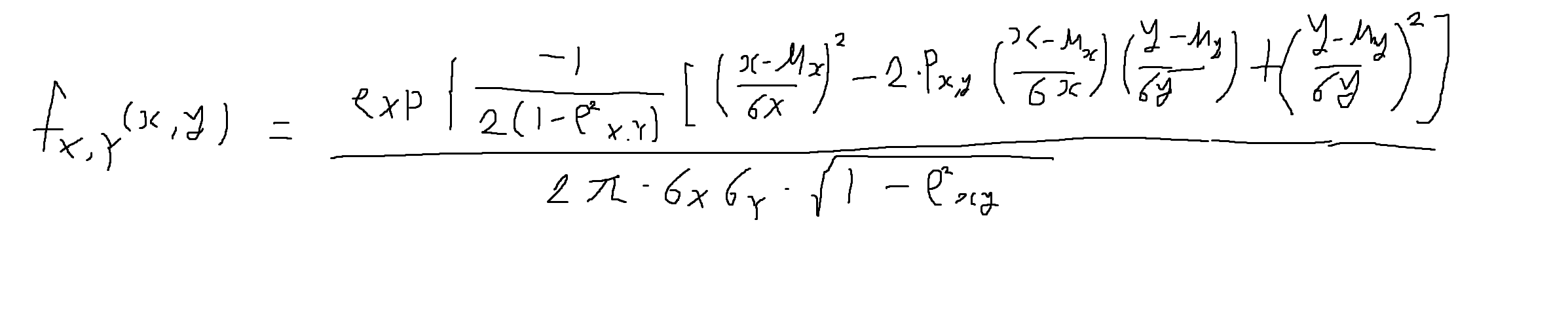
-
(복습) 공분산 (covariance)
cov[X, Y] = E[(X-mx) (Y-my)] = E[XY] - E[X] * E[Y] -
(복습) 상관계수 (correlation coefficent)
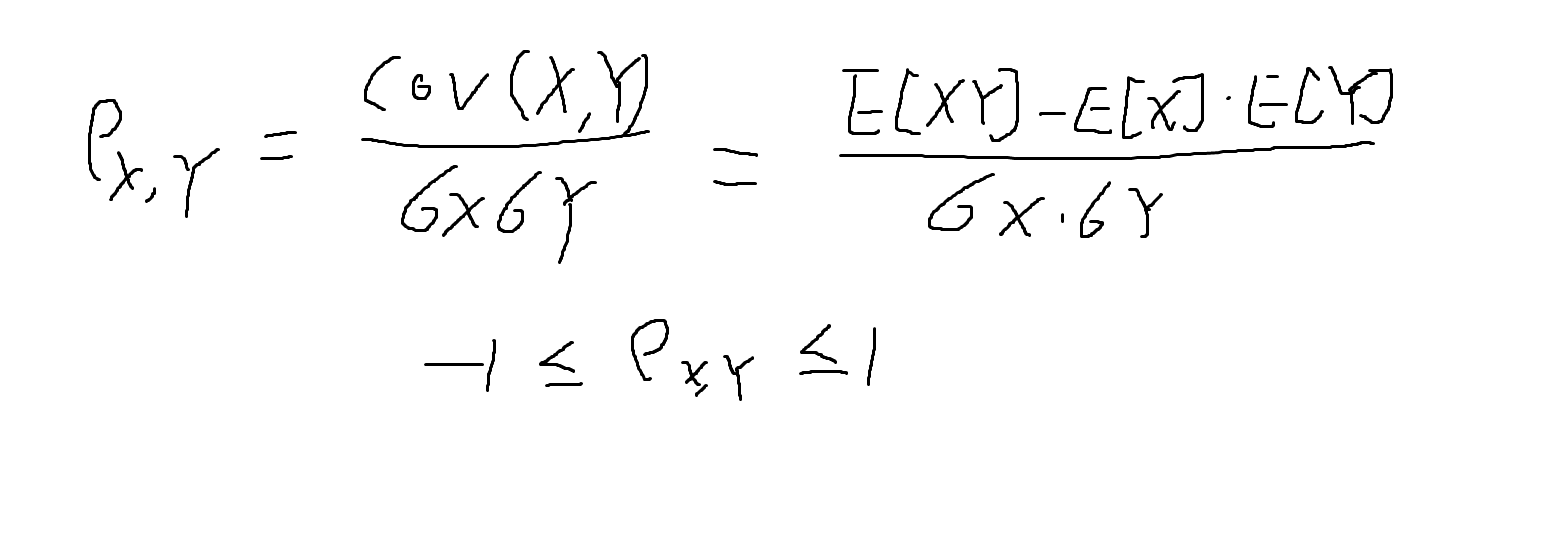
-
특정 상관계수 값(ρ)을 가지는 표준정규분포 (평균 0, 분산 1) 쌍 생성 방법
-
독립인 두 가우스 확률변수의 합
-
X~N(µx, σ²x), Y~N(µy, σ²y)
-> Z = X + Y(µx + µy, σ²x + σ²y)
-> 여기서 X, Y는 독립
-> 독립일 경우, 두 가우스 확률변수의 합은 여전히 가우스 확률변수이다.
-> Z, X는 독립? No. (Z, Y)도 마찬가지
특정 상관계수 값(ρ)을 가지는 표준정규분포 (평균 0, 분산 1) 쌍 생성방법
- 서로 독립인 표준정규분포 X, Y에 대해 다음을 생각해보자.
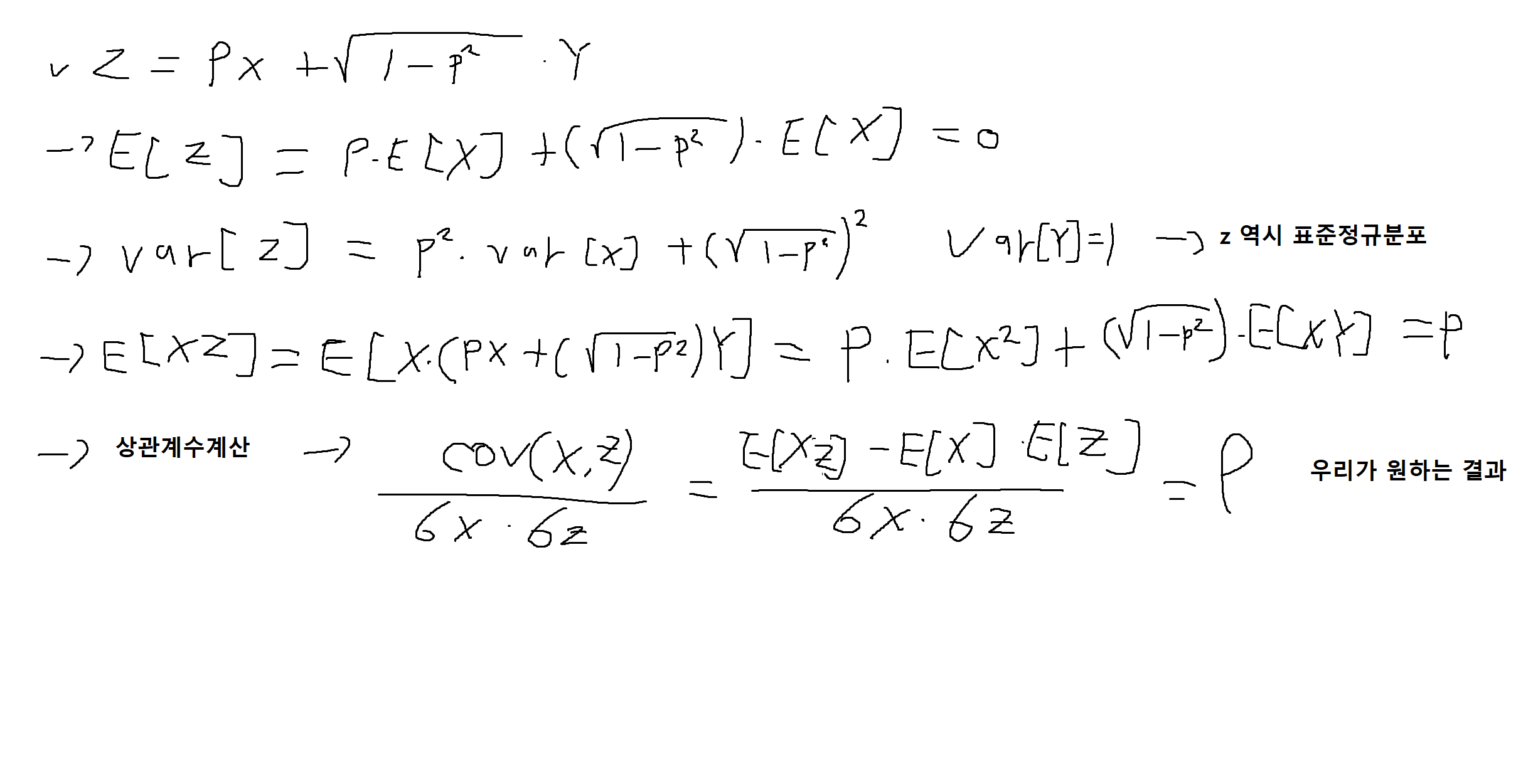
특정 상관계수 값(ρ)을 가지는 표준정규분포(평균 0, 분산 1) 쌍 생성방법
-
서로 독립인 표준정규분포 X, Y을 어떻게 만들 수 있을까?
-
Box-Muller 방법 -> 서로 독립인 표준정규분포 X, Y을 따르는 난수 생성

특정 상관계수 값(ρ)을 가지는 표준정규분포 (평균 0, 분산 1) 쌍 생성방법
(1) Box-Muller 방법 이용 -> (xk, yk) 순서쌍 샘플 생성
(2) 주어진 상관계수 값(ρ) -> zk = ρxk + (1-p^2)^(1/2) * yk 샘플 생성
(3) (xk, zk) 순서쌍 -> 상관계수가 ρ 표준정규분포 순서쌍의 샘플
