T/F 확인문제
(1) 두 확률변수 X, Y에 대해, E[XY] = E[X] * E[Y]이 성립하면 XY는 독립이다.
-> F (반대만 참)
cov(X, Y) = E[XY] - E[X] E[Y] = 0 -> ρx,y = 0 ≠> 독립
(2) 확률변수 X의 평균(E[X])과 분산(Var[X])은 각각 3, 1이고, 확률변수 Y의 평균과 분산은 각각 2, 4일 때, 항상 E[XY] <= 12이다.
-> T
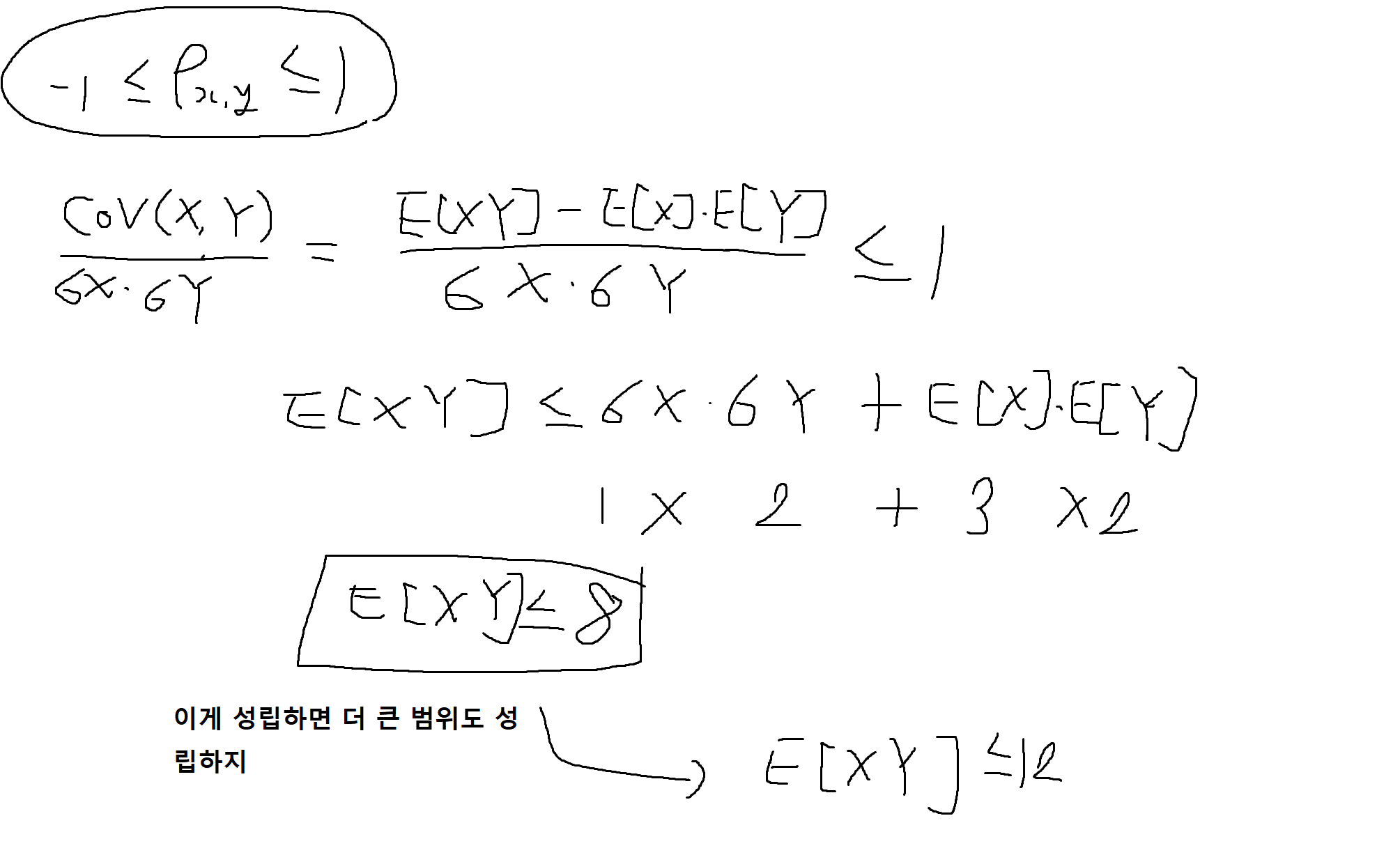
두 확률변수의 조건부 확률
-
(복습) 조건부확률
-
사건 B가 이미 발생했을 때 A의 발생확률 : P[A|B] = P[A∩B] / P[B]
두 확률변수 (X, Y)의 조건부 확률
- 확률변수 Y가 사건 A에 대응, X가 사건 B에 대응하는 경우
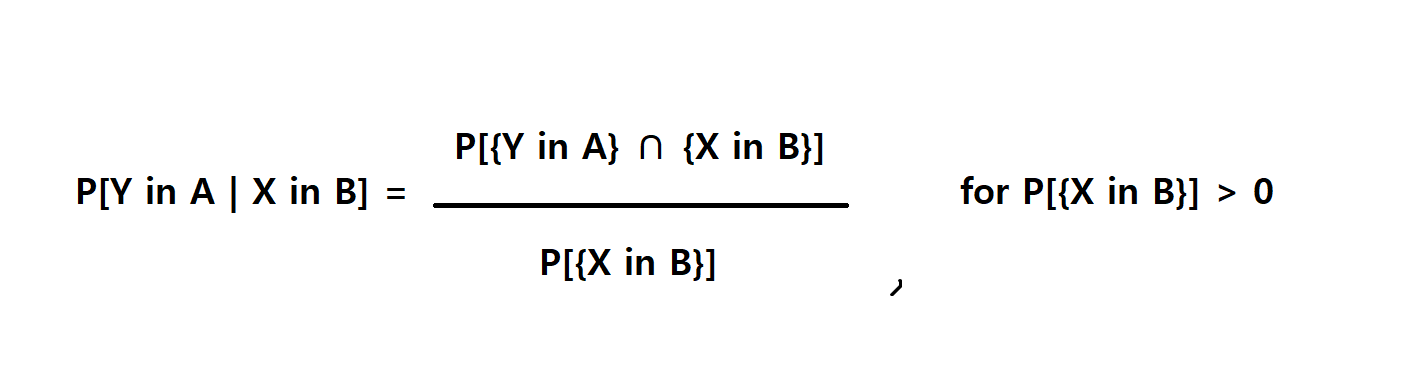
- 확률변수 X, Y의 형태(이산/ 연속)에 따라 여러 계산방법이 존재
- [Case 1-1] X : 이산확률변수, Y : 이산확률변수
조건부 확률질량함수 (conditional PMF)
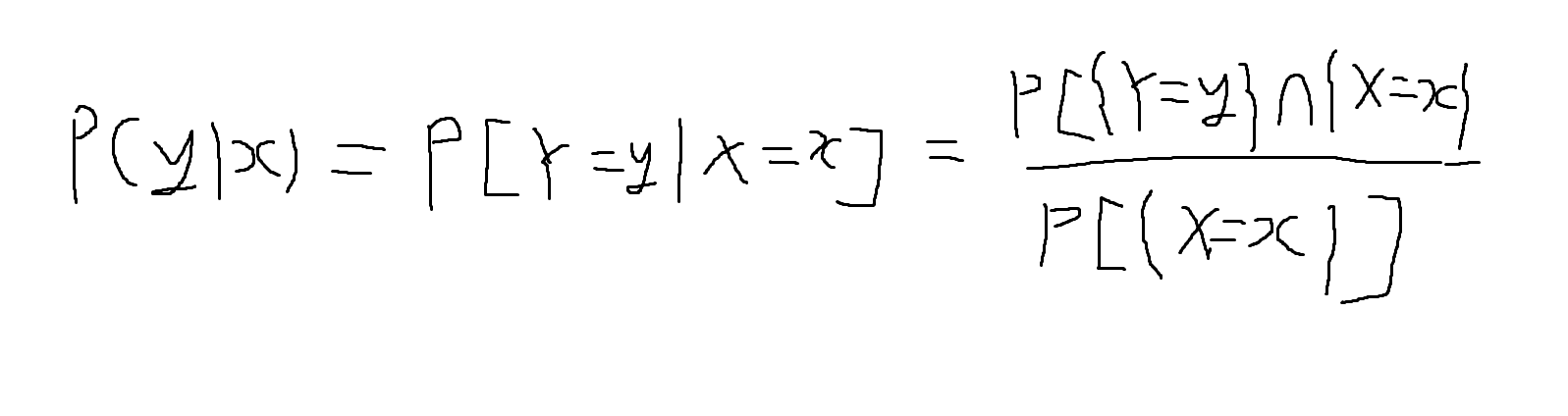
- [Case 1-2] X : 이산확률변수, Y : 연속확률변수
조건부 누적분포함수 (conditional CDF)
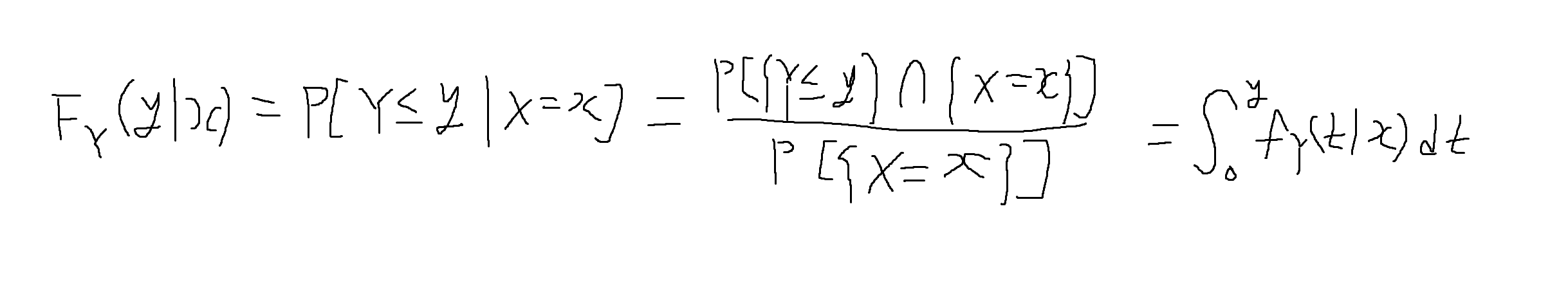
예제 5-21 : X는 1/3과 2/3확률로 +1 또는 -1의 값을 가지는 확률변수이고, W는 평균이 0이고 분산이 1인 가우스 확률변수이다. 어떤 통신시스템의 수신출력이 Y = X + W 일 때, P[X = +1 | Y > 0]의 값을 구하여라.
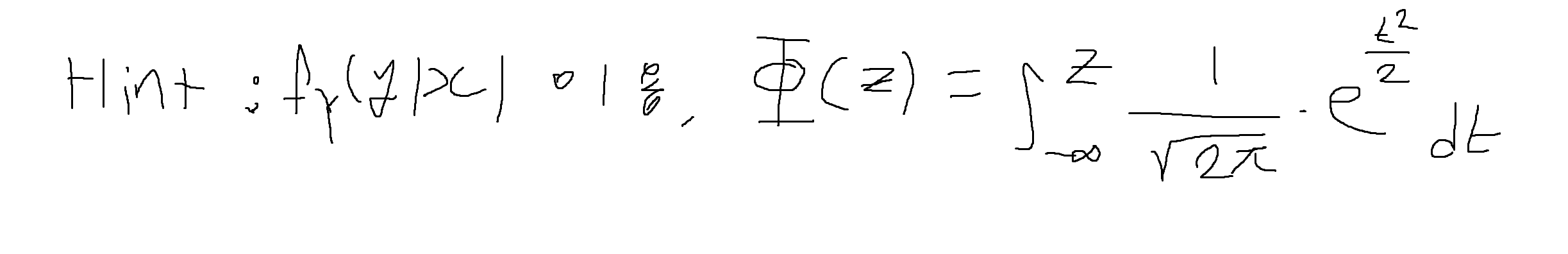

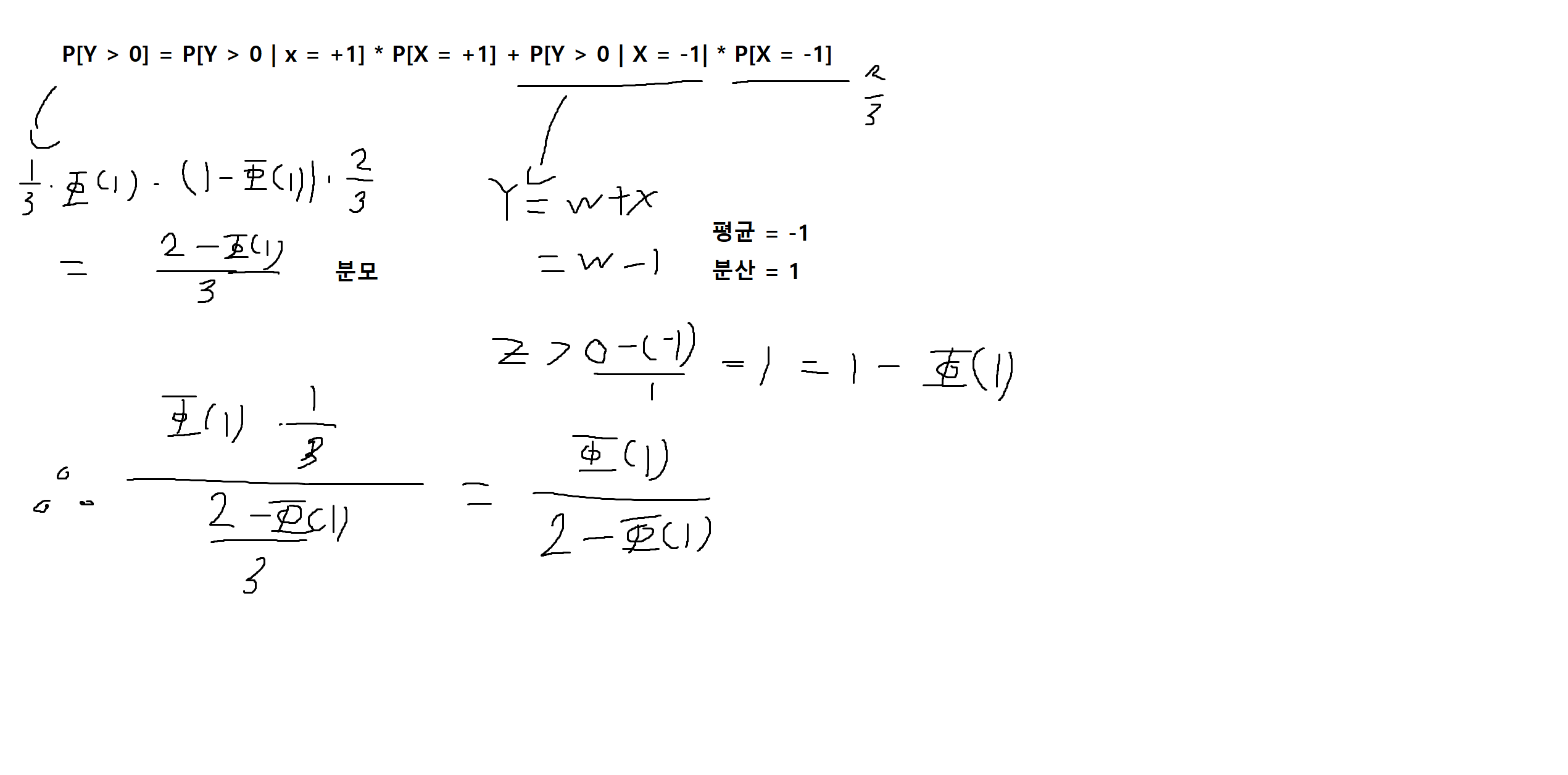
[Case 2] X : 연속확률변수, Y : 이산/연속확률변수
- 조건부 확률밀도함수 (Conditional PDF)

예제 5-22 : 아래의 fx,y(x,y)가 결합확률밀도함수(joint PDF)일 때, fx(x|y), fy(y|x)을 구하여라. (* Hint : 구간에 유의)
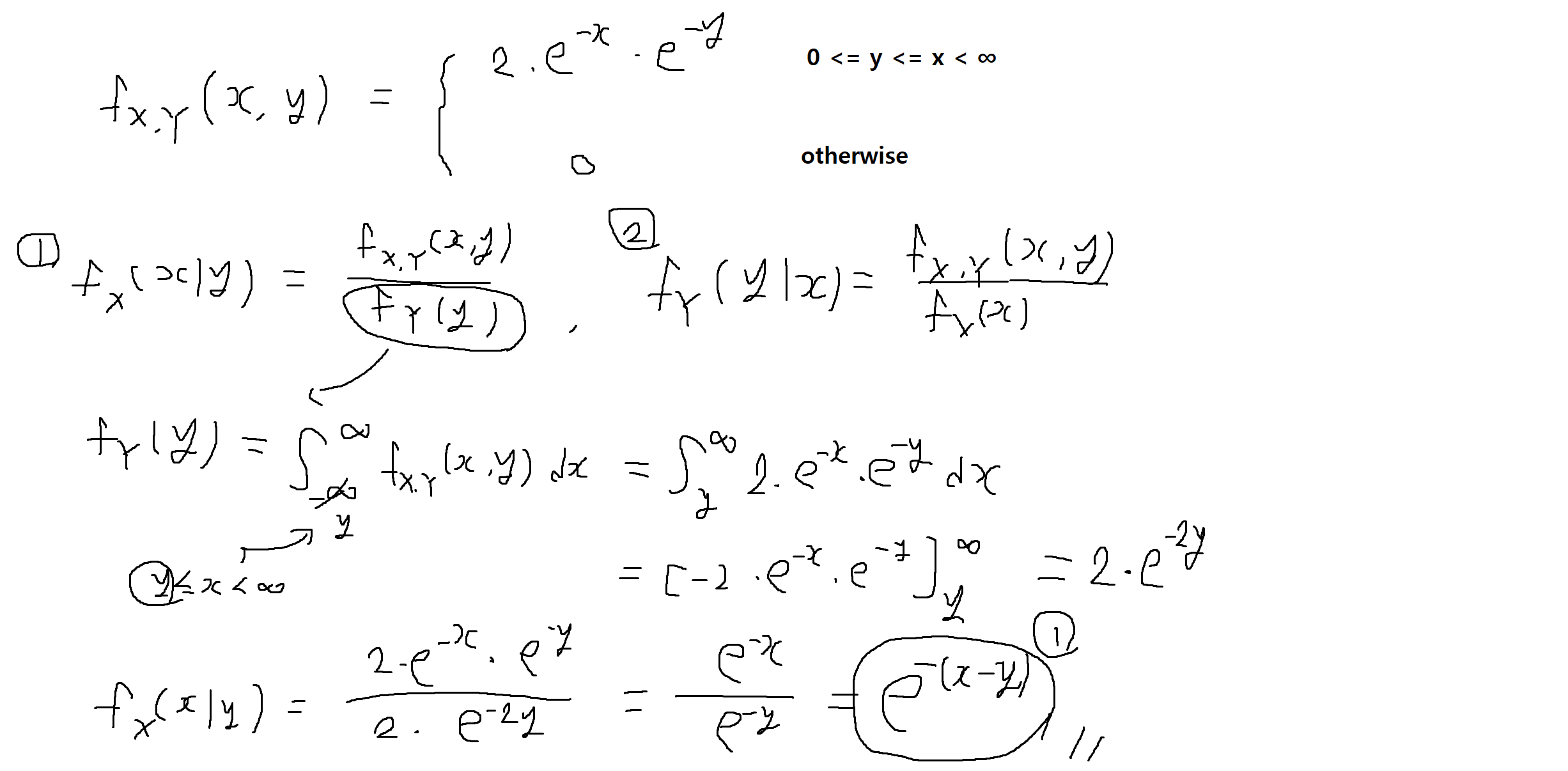
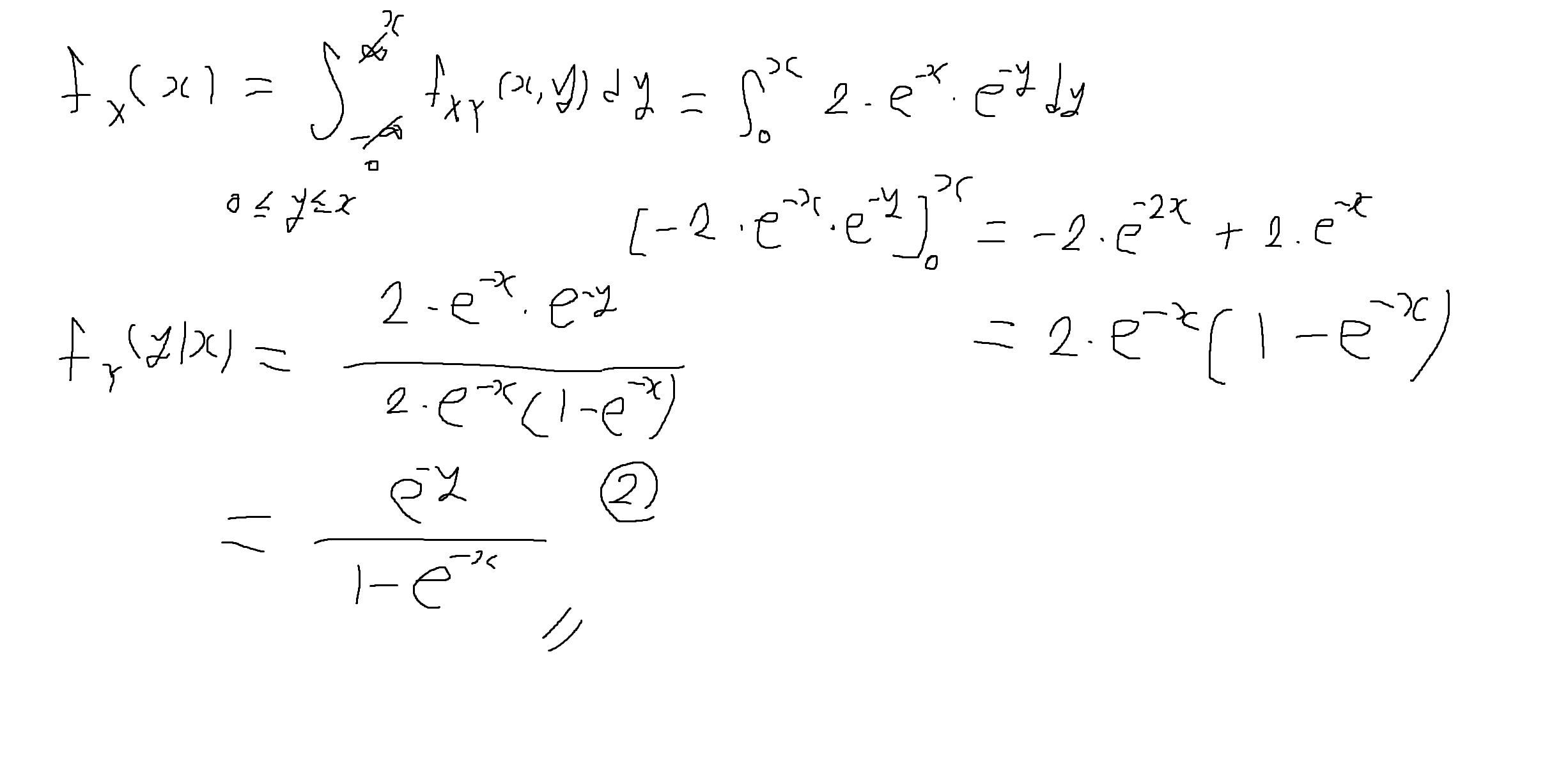
예제 5-23 : 예제 5-21에서 Y = y일 때, X = +1일 확률, 즉, P[X = +1 | Y = y]의 값을 구하여라.
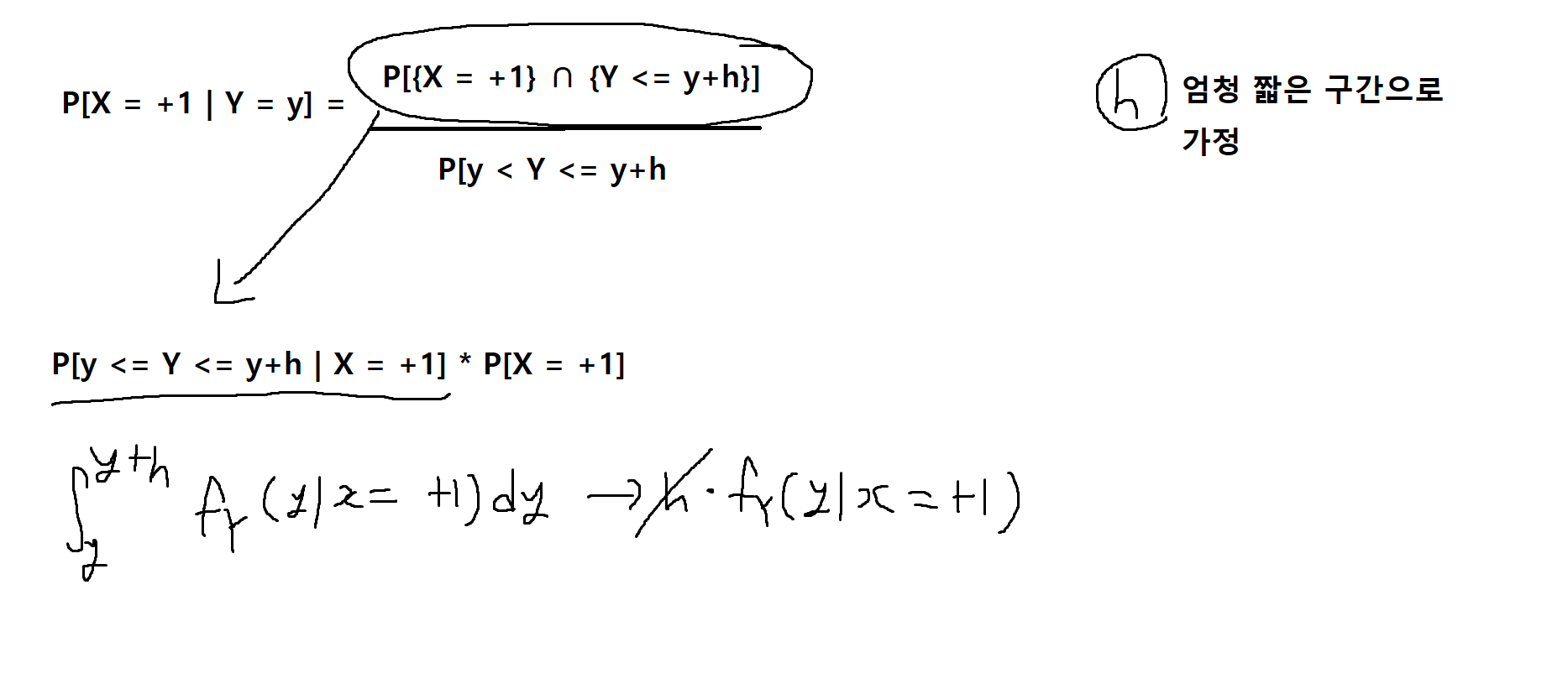
두 확률변수의 함수
- 우리의 관심 : 확률실험의 특성 파악
- 어떻게? 확률변수를 이용 -> 하나의 확률변수 vs 여러 개의 확률변수
(잘 알려진) 이산/ 연속확률변수 : X -> (학습 O)
확률변수의 함수 : Z = g(x) -> (학습 O)
두 확률변수 : (X, Y) -> (학습 O)
확률변수 Z = g(X, Y) -> (학습예정 O)
확률변수함수 (일반화)
(z1,...,zn) = g(x₁,...,xn) -> 여려움 : 학습(X)
(복습) Y = g(X)일 때, X의 CDF Fx(x)를 이용하여 Y의 CDF Fy(y)를 표현
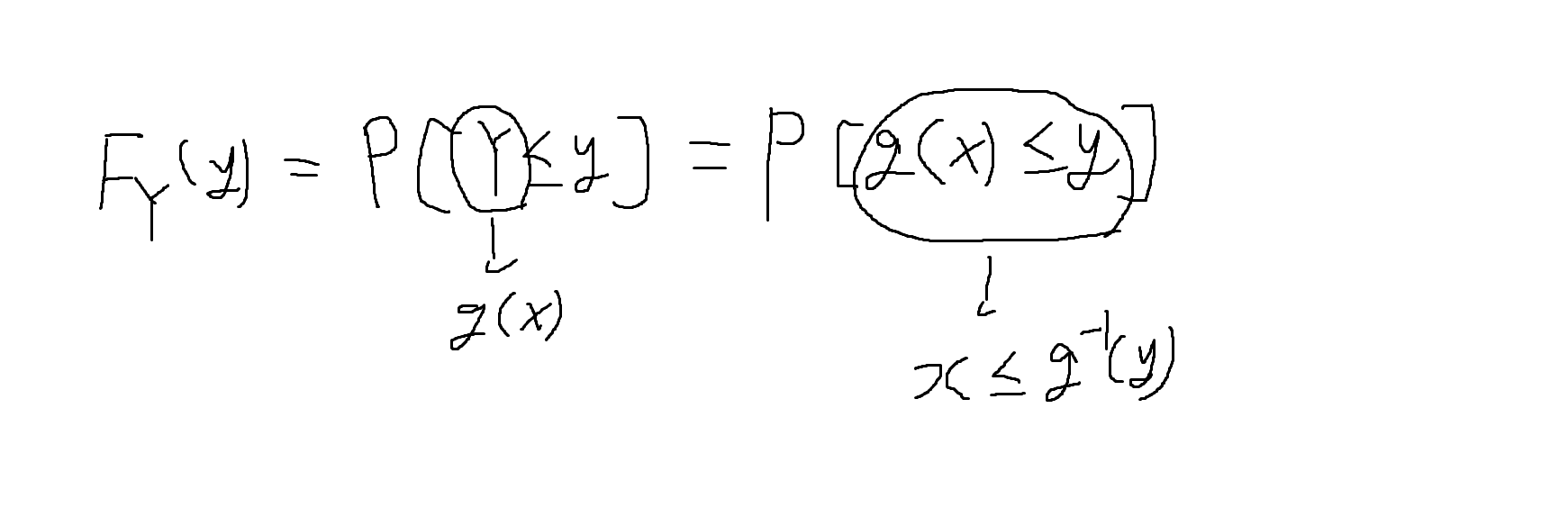
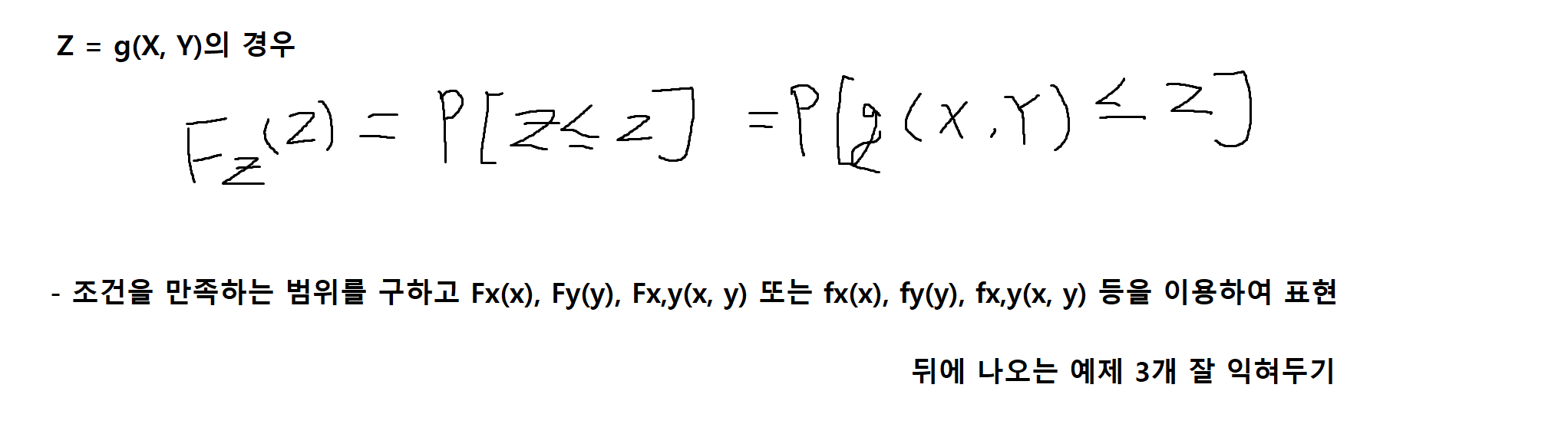
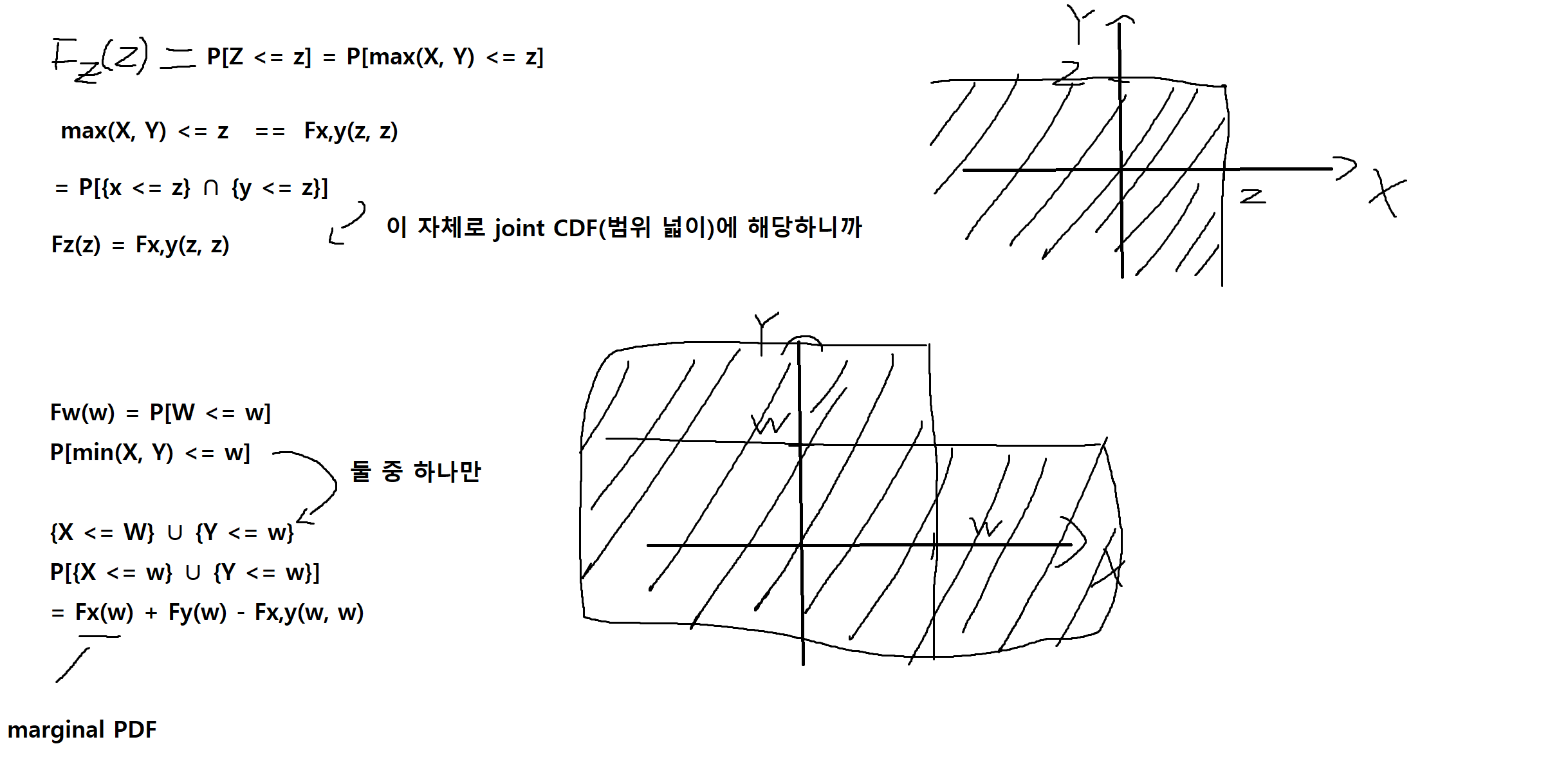
예제 5-24 : 두 확률변수 X, Y에 대하여, Z = max(X, Y), W = min(X, Y) 일 때, Z, W의 CDF를 구하여라.
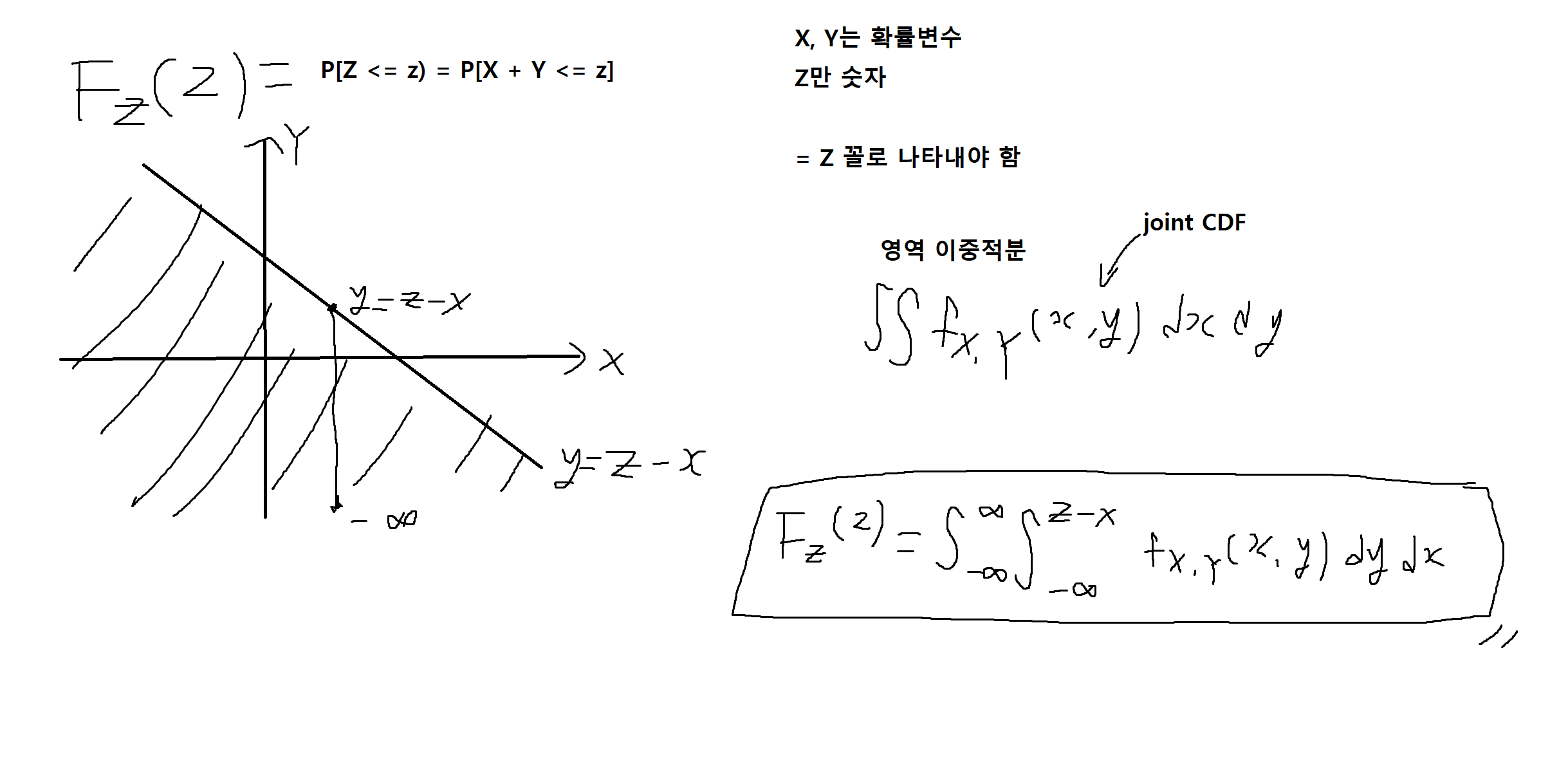
예제 5-25 : 두 확률변수 X, Y에 대하여 Z = X + Y일 때, Z의 CDF를 구하여라.
예제 5-26 : X, Y가 각각 평균이 1이고, 독립인 지수확률변수일 때, Z = X / Y의 CDF와 PDF를 구하여라.

