복습(T/F 확인문제)
(1) 두 사건 A,B가 독립일 경우, P[A∪B] = P[A] + P[A^c]P[B]이다.
독립 -> A∩B = P[A] P[B]
P[A∪B] = P[A] + P[B] - P[A∩B]
= P[A] + P[B] (1-P[A])
= P[A] + P[A^c] * P[B]
-> T
(2) 두 이산확률변수 X,Y에 대해, Y = -X +10일 때, X,Y의 분산은 같은 값이다.
(분산은 더하거나 빼기는 없애도 되고, 앞에 곱해진 값은 제곱이 되서 나온다)
(기대값에서는 둘다 그냥 나옴)
V[Y] = V[-X+10] = (-1)^2 * V[X] = V[X]
-> T
(3) 이산확률 변수 X에 대해, X의 기대값이 0일 경우 X의 분산은 X의 2차 모멘트와 같은 값이다.
Var[X] = E[X²] - mx²
Var[X] = E[X²]
-> T
(4) 성공확률이 p = 1/2인 베르누이 확률변수 X에 대해서 E[2X] = E[X²+1/2]을 만족한다.
베르누이 확률변수 -> 성공을 1, 실패를 0으로
E[X] = 11/2 + 0 1/2 = 1/2
E[X²] = 1² 1/2 + 0² * 1/2 = 1/2
E[2X] = 2 E[X] = 2 1/2 = 1
E[X²+1/2] = E[X²] + 1/2 = 1
1 == 1
-> T
예제 3-13. 동전을 7번 던졌다고 가정, 각 동전던지기는 $d의 비용이 들며, X는 앞면 나온 횟수일 때, 상금 aX+b를 받게 된다. 이때, 던지기 비용과 상금을 포함한 이익의 기댓값을 구하시오
베르누이 시행 독립적 n번, 그 중 k번 성공을 가정
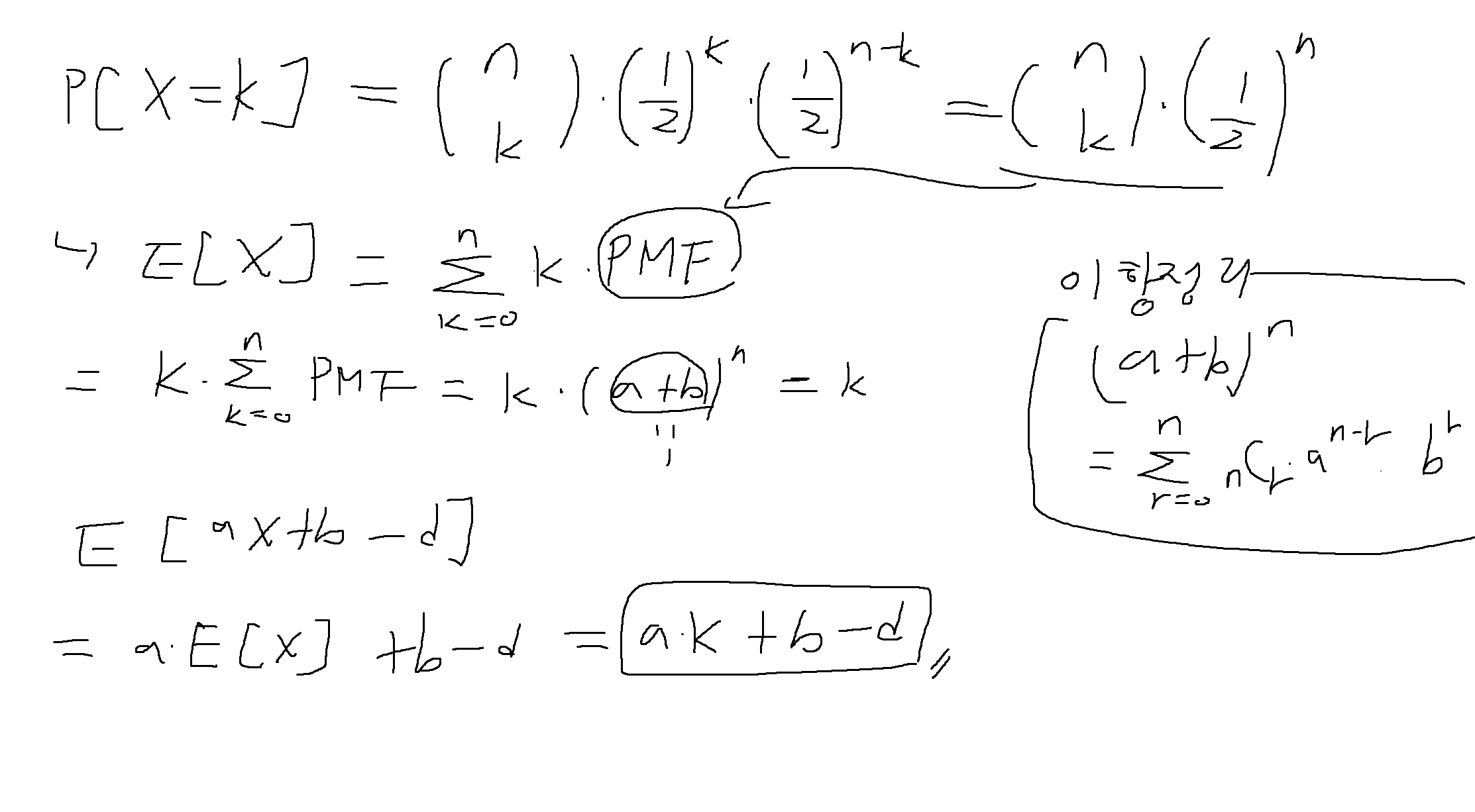
조건확률 질량함수(CPMF = conditional probability mass function)
-
확률변수 X 또는 확률실험의 결과에 대한 부분적인 정보를 가지고 있을 경우, 부분정보에 대한 조건하에 확률질량함수 (PMF)를 생각할 수 있다.
-
사건 C가 주어졌을 때 (부분정보), 조건부확률의 정의를 활용하여 CPMF는 다음과 같이 정의된다.
Px(x|c) = P[{X=x} ∩ C] / P[C] -
앞의 베이즈 정리와 목적이 비슷함 (그냥 구하기 어려우니까 이렇게 구해보겠다는 것)
P[R0] = P[R0|T1] P[T1] + P[R0}T0] P[T0]

예제 3-14. 공장에서 생산라인은 두가지 종류의 소자를 생산한다. 소자 1은 확률 α로 생산하고 소자 2는 확률 1-α로 생산한다. 각 장치의 수명은 기하확률 분포를 따른다. X를 임의의 소자 수명이라고 하고 B₁,B₂은 소자 종류 1,2의 생산에 관한 사건이라고 할때, 각 CPMF와 PMF를 구하시오.
(Hint : 기하확률분포 PMF, Pz(k) = (1-P0)^k-1 * p0 -> (k-1번 고장, k번째 성공)
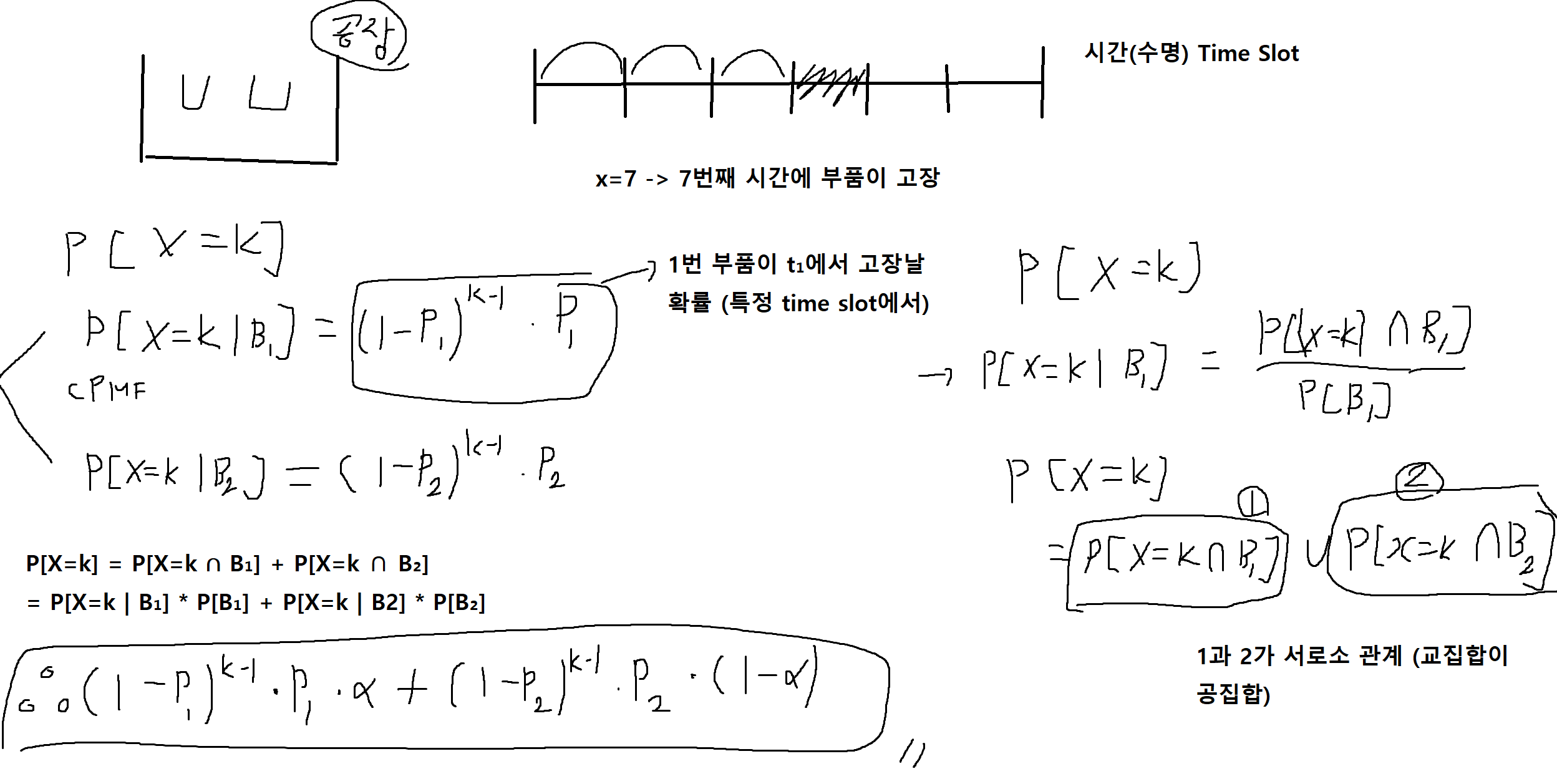
- CPMF가 PMF보다 작은 단위 (각 조건별 CPMF들의 합 -> PMF)
예제 3-15. 예제 3-14에서 확률변수 X의 기대값과 분산을 구하시오

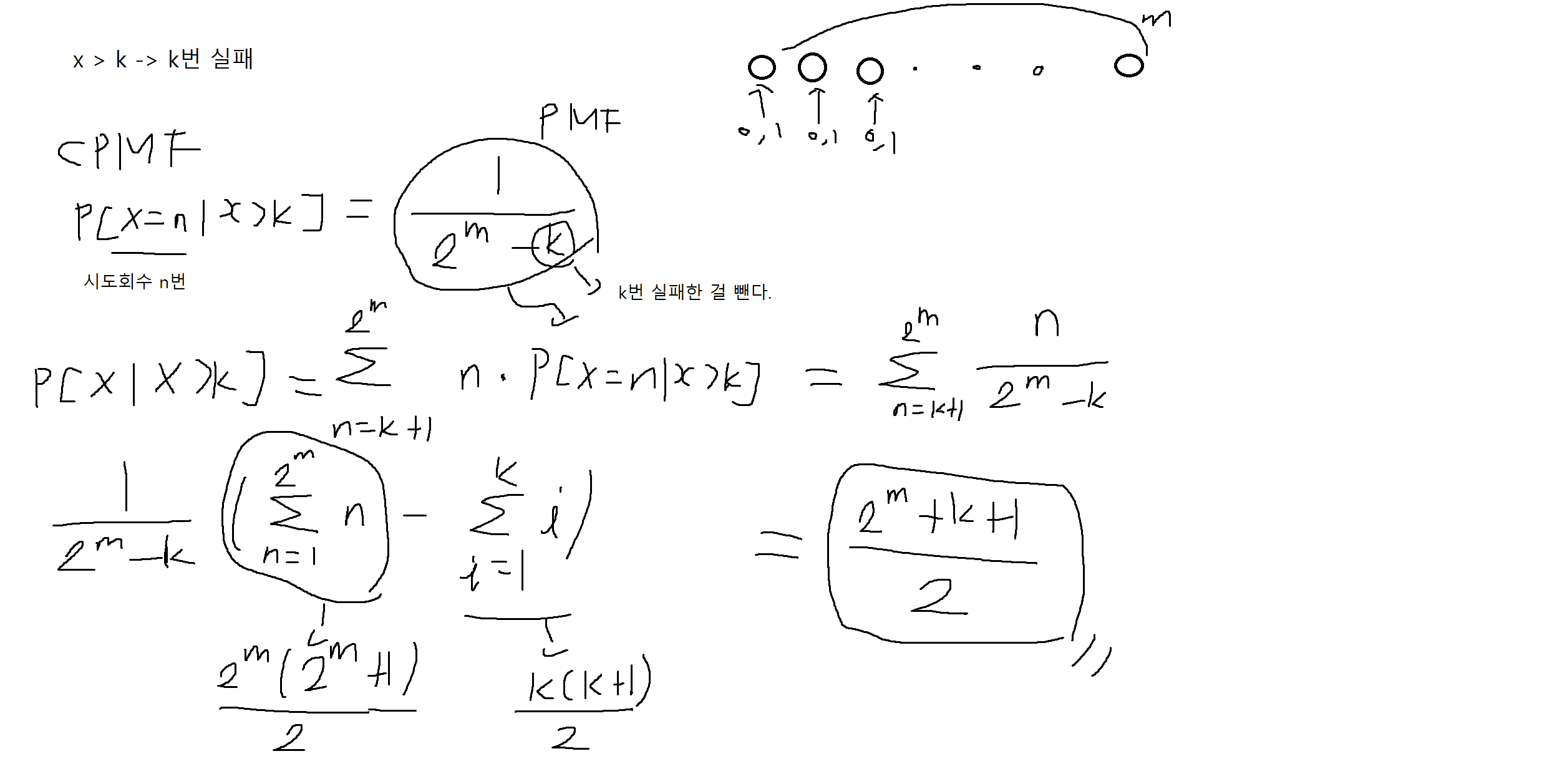
예제 3-16. 어떤 시스템에 접속하기 위해 m-bit 비밀번호가 필요하다. 해커는 모든 가능한 m-bit 패턴을 체계적으로 동작시킨다. 확률변수 X는 해커가 비밀번호를 찾을 때까지 시도한 패턴의 수이다. 이때, E[X | X>k]를 구하여라
m-bit의 비밀번호면 전체가 2^m 개라는 것
X > k -> k번 실패
이항확률변수
-
확률실험이 독립적으로 n번 반복
-
X:n번 실행 중 사건 A(확률 p)가 일어나는 횟수
-
n개의 베르누이 확률변수의 합 : X = I₁+I₂+...+In
-
PMF : P[X=k] = nCk * P^k (1-p)^(n-k)
-
기대값 : E[X] = np
-
분산 : Var[X] = np(1-p)
ex) 동전 확률 p = 1/2, 100번 시행
E[x] = 1/2 100 = 50
Var[x] = 100 1/2 * 1/2 = 25
기하확률변수 -> Sm = {1,...,∞}
-
M : 사건 A(확률 P)가 성공할때까지 반복되는 베르누이 시행의 수 k
-
PMF : P[M=k] - p * (1-p)^(k-1)
-> k-1번 실패, k번째에서 성공 -
기대값 : E[M] = 1/p
-
분산 : Var[M] = (1-p) / p²
-
P[M <= k] = ?
= P[{M=1} ∪ {M=2} ∪ ... ∪ {M=k}]

포아송 확률변수
-
N : 어떤 시간범위 (공간 영역) 이내에서 사건의 발생횟수
-
α : 주어진 시간범위 (공간 영역)에서 "평균" 사건발생 횟수(α) - 시간단위 고려

예제 3-17. 콜센터에 t초 안에 도착하는 문의(query) 개수 N은 λ가 문의/초 로 평균도착률인 α = λt를 갖는 포아송 확률변수이다. 도착률 (λ)은 분당 4개 문의라고 가정한다.
(1) 10초안에 4개의 문의보다 많을 확률
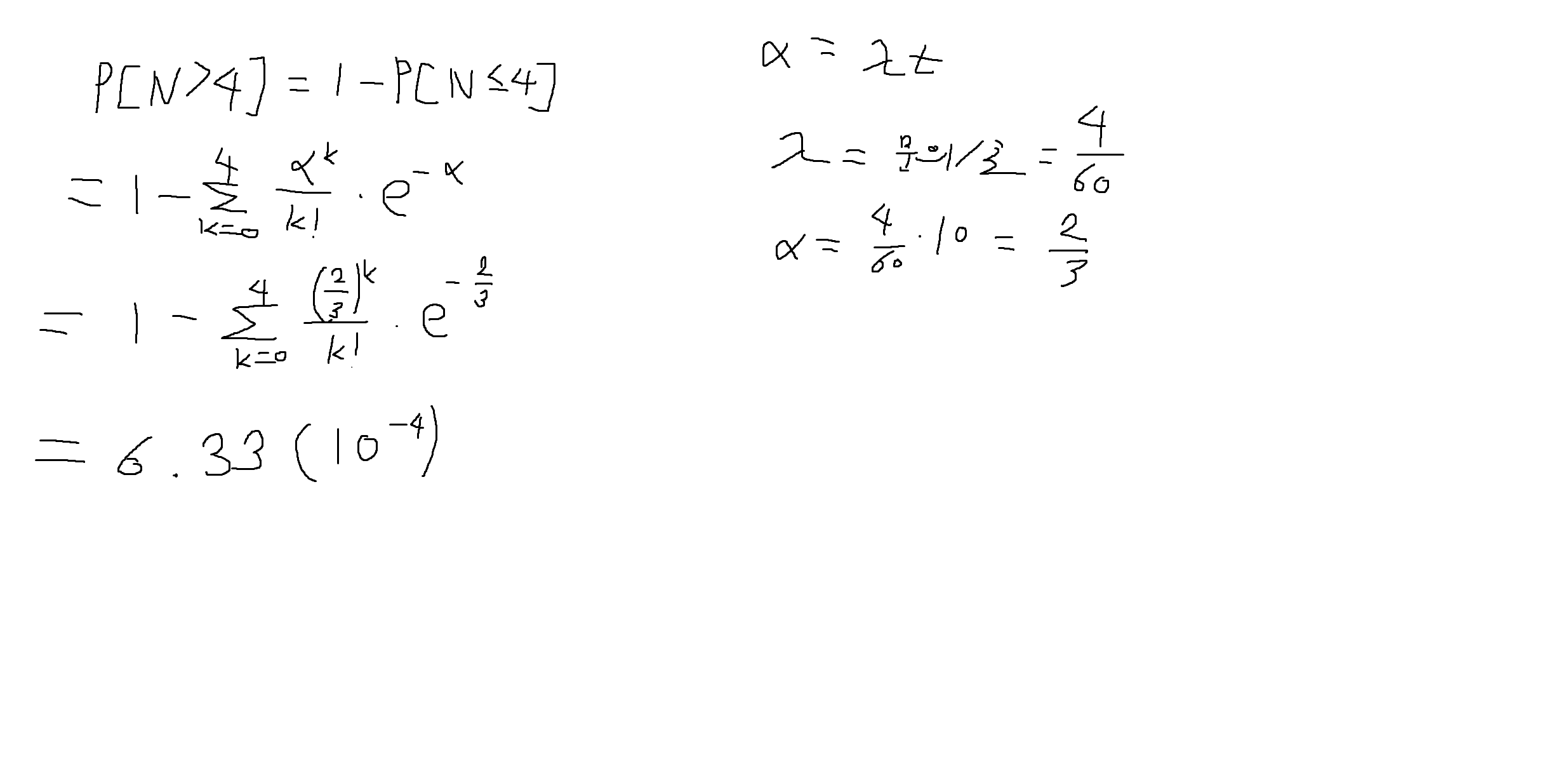
(2) 2분안에 5개의 문의보다 적을 확률
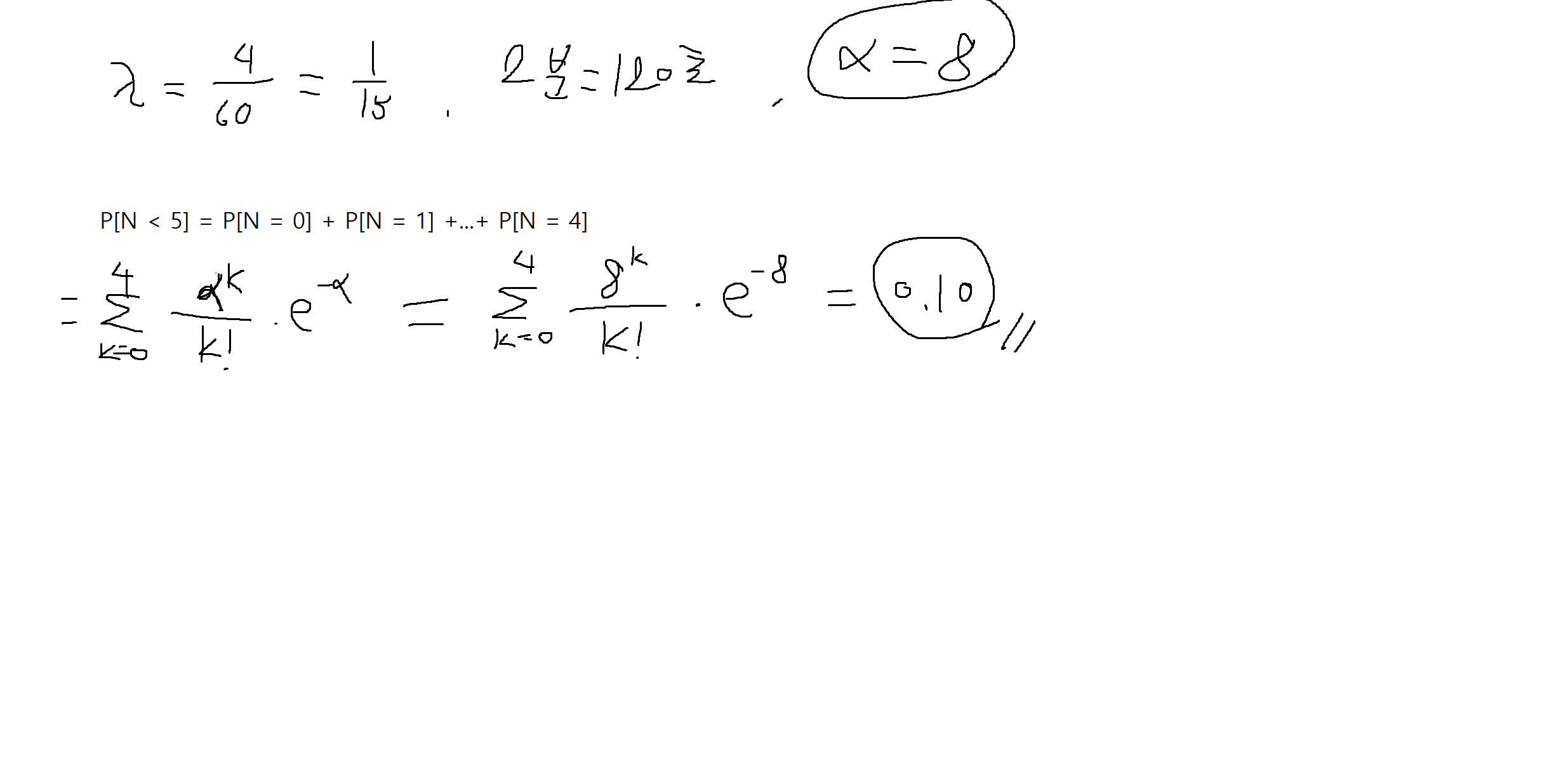
예제 3-18. 웹 서버에 도착하는 페이지 요청 수는 평균 "분당" x회이며, 포아송 분포를 따른다. (즉, 특정시간의 구간 동안 도착하는 페이지 요청수는 포아송 확률변수가 된다.) 이때, "1초 구간"동안 페이지 요청이 없을 확률이 1/e²보다 작거나 같아지는 x의 최소값을 구하시오.
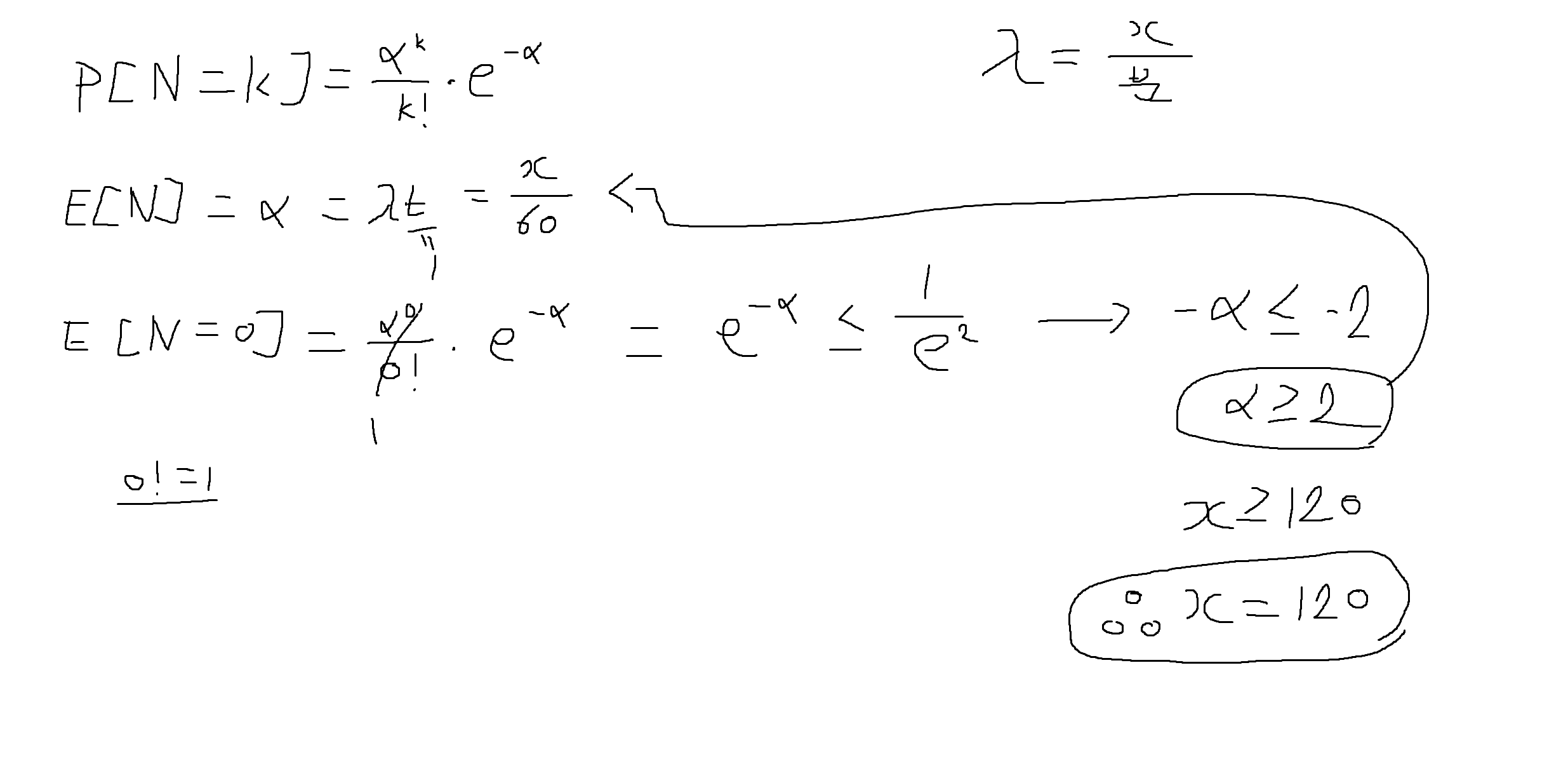
- 우리의 관심 : 확률변수 X의 특성
| 이산확률변수 | 연속확률변수 |
|---|---|
| PMF (확률질량함수) Px(x) = P[X=x] | 일반적인 확률변수에서는 각 개념(PMF, 기대값, 주요 RV등)이 |
| 기대값, 분산 | (가능하다면) 확장적용될 수 있을까?, (불가능하다면) 어떤 개념이 필요한가? |
| 베르누이/이항/기하/포아송 |
-
확률실험의 표본공간을 확률변수 X 가질 수 있는 값, 그 확률의 분포 -> 확률분포
-
이산확률변수에서는 확률질량함수 PMF 이용
-
확률분포의 특성을 기대값, 모멘트 등으로 이용하여 좀 더 세분화 가능
PMF의 문제점 : 이산확률 변수에서만 정의가능
- PMF에서는 {X=b}사건의 확률은 구체적으로 정의
- 연속표본공간에서 : {X=b} 사건의 확률은 0
- 연속표본공간에서는 하나의 점이 아니라 범위를 고려 {X <= b}
ex} Sx = {x | 0<=x<=1, x∈R}
P[X = 0.3] = 0
P[X <= 0.5] = (1/2)/1 = 1/2
누적분포함수 (CDF) : 확률변수 X의 사건 {X<=x}의 확률에 관한 함수 (-∞ < x < ∞)
Fx(x) = P[X <=x]
-> 확률변수 X의 값이 (-∞, x)구간에서 존재할 확률
동전던지기 실험
X=x : 앞면이 나올 횟수
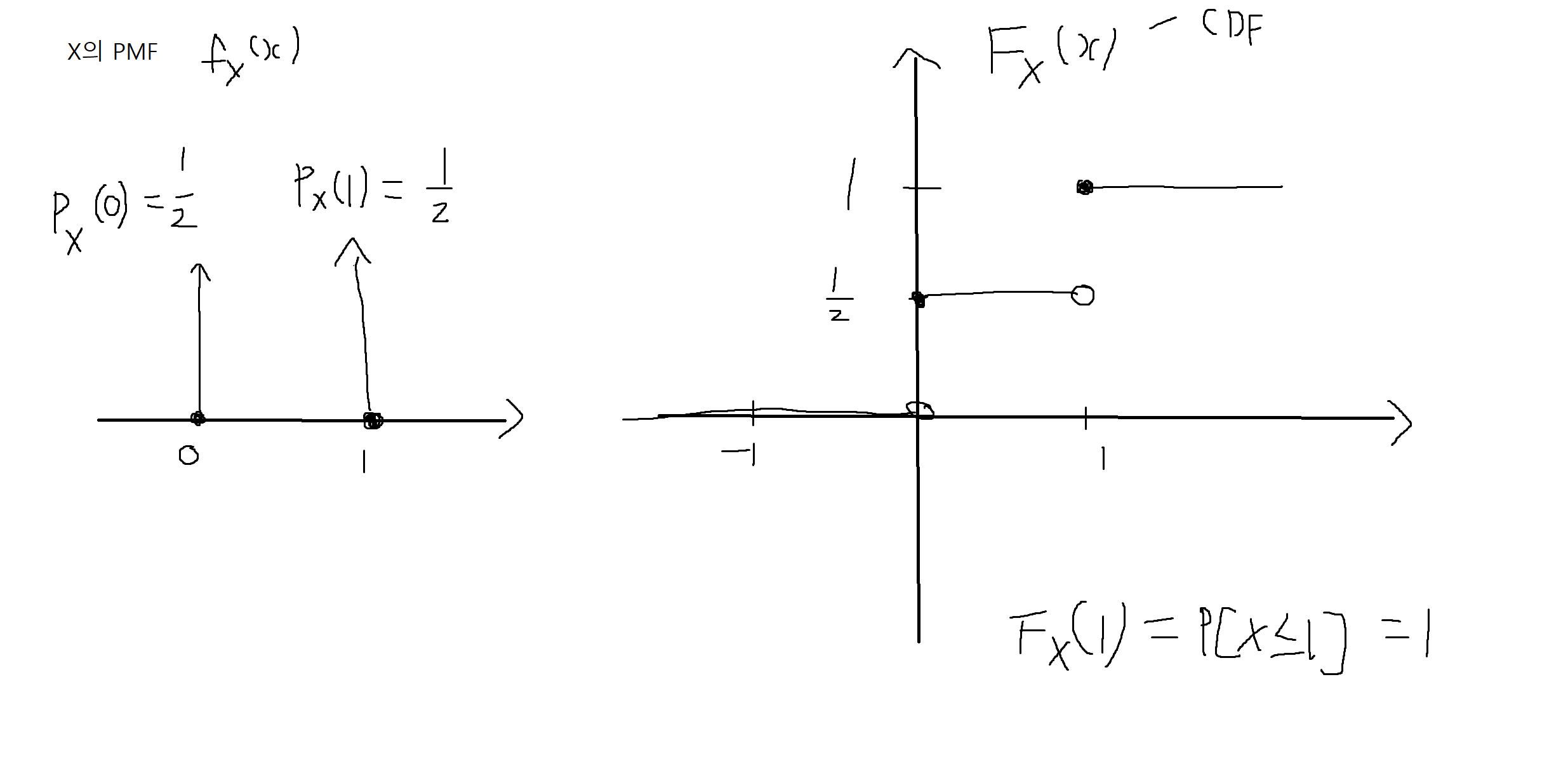
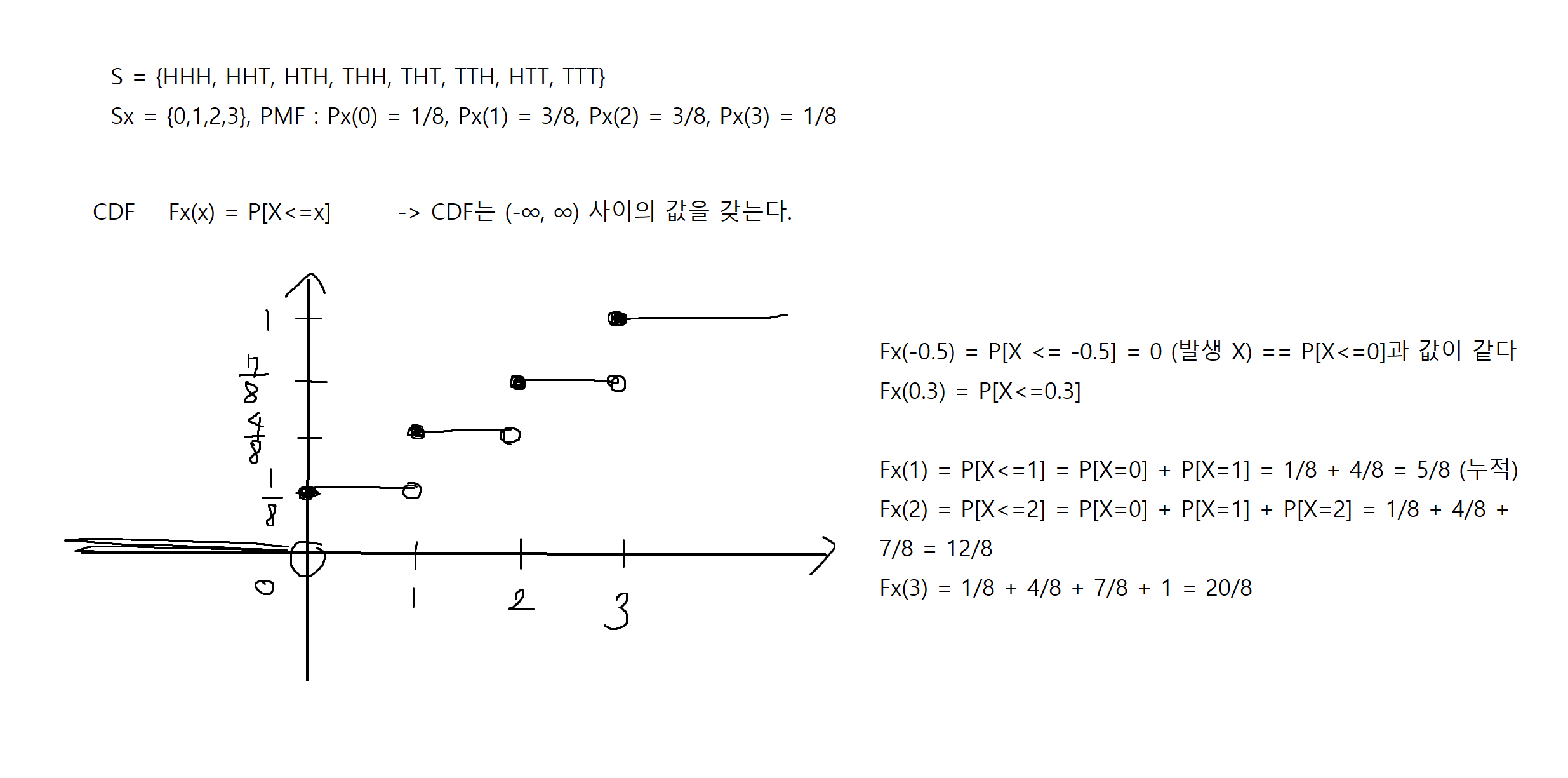
예제 4-1. 동전을 세번 던져서 나온 앞면의 수를 확률변수 X의 PMF와 CDF를 구하시오.
예제 4-2. 원형판의 중심에 화살을 붙여 돌린다. Θ를 화살이 멈췄을 떄 각도 (0~2π)로 정의했을 때, Θ가 특정구간에 놓일 확률은 구간의 길이에 비례한다. X(Θ) = Θ/2π로 정의했을 때, X의 CDF를 구하시오 (균등확률함수 : Uniform random variable)
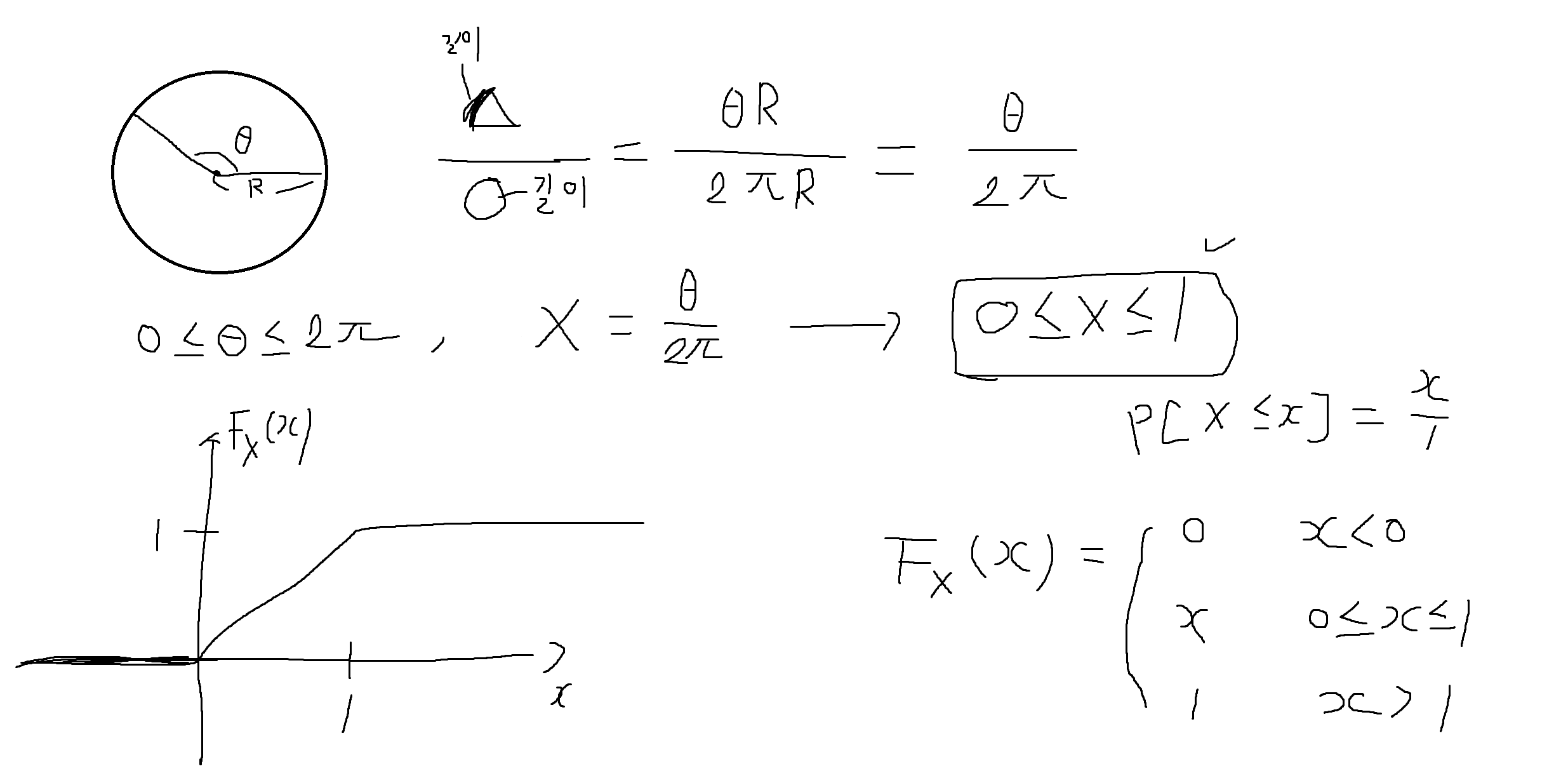
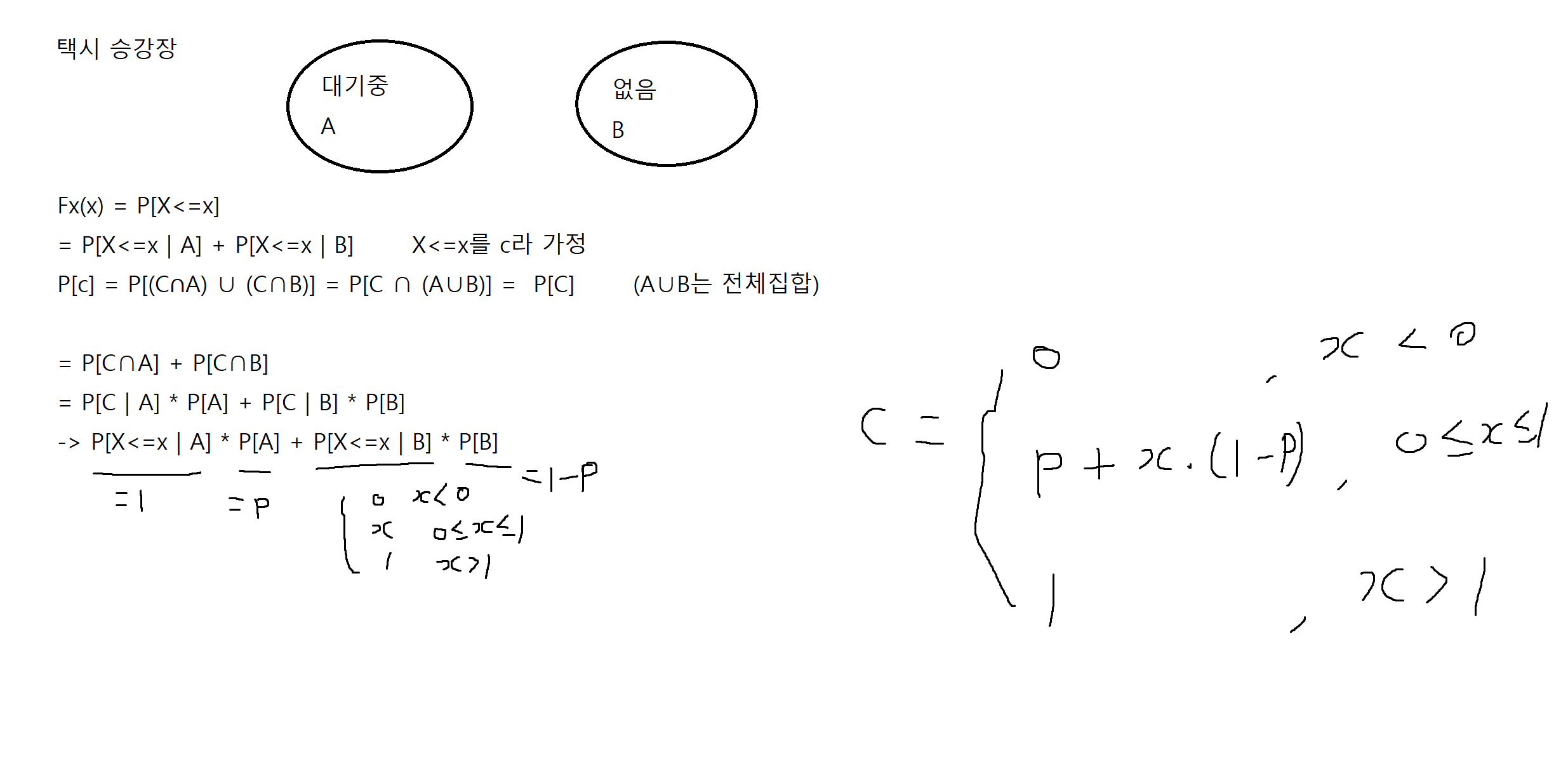
예제 4-3. 택시 승강장에서 고객의 기다리는 시간 X는 택시승강장에 대기중인 택시가 있다면 0이고 택시가 없다면 0과 1사이에서 균등하게 분포한다. 고객이 승강장에 도착했을 때, 택시가 있는 확률이 P일 때, X의 CDF를 구하시오.
택시가 있을 확률 p -> 없을 확률 1-p
예제 4-4. X는 공정한 동전을 세번 던져서 나온 앞면의 수이다. CDF를 이용하여 사건 A = {1 < x<= 2}, B = {0.5 <= x <= 2.5}, C = {1 <= x <= 2}의 확률을 구하시오.

