기댓값과 모멘트
- 확률변수 X의 특성 : 확률변수 X 가질 수 있는 값, 그 확률의 분포 -> 확률분포
- 이산확률 변수에서는 확률질량함수(PMF) 이용
- 확률분포의 특성을 파악할 수 있는 수치 -> 기대값(평균), 모멘트
1차 모멘트 = 기대값, 2차 모멘트 = 분산
확률분포 (정확히 알기 어렵다) -> 기대값과 모멘트를 활용
| Case 1 | Case 2 | Case 3 |
|---|---|---|
| 80점 | 80점, 평균 70점 | 80점, 평균 70점, 분산 10 |
-> 경우에 따라 알 수 있는게 다르다.
- 기대값 또는 평균은 다음과 같이 정의된다.

예제 3-9 : 세 번 동전던지기에서 앞면의 수가 2이면 $1을 받고, 그 수가 3이면 $8을 받지만, 그 외의 경우는 $0을 받는 게임이 있다. 게임 참가비가 $1.5이고 게임참가로 얻을 수 있는 이익을 Y라 할 때, Y의 기대값을 구해라.
치역 : Sx = {0, 1, 8}
-> Px(0) = 1/2
-> px(1) = 3/8
-> px(9) = 1/8
Y = X - 1.5
Sy = {-1.5, -0.5, 6.5}
Py(-1.5) = 1/2
Py(-0.5) = 3/8
Py(6.5) = 1/8
E[Y] = -1.5 1/2 + (-0.5 3/8) + (6.5 * 1/8)
= -1/8
예제 3-10 (교재 3-15 변형) : X를 동전의 앞면이 나올 확률이 P인 동전을 앞면이 나올 때까지 던진 횟수라고 할 때, X의 기대값을 구하시오
(Hint : 1/1-x = sum k=0 to ∞ x^k)
Sx = {1, 2, 3...∞}
Px(n) = (1-p)^(n-1) * p
-> n-1번은 실패하고 n번째에서 성공함

-
확률변수함수 : 확률변수에서 또 다른 확률변수로의 대응 (즉, Z = g(x))
-
세 번의 동전던지기 예제에서 보상 (0, $1, $8)과 이익 (-1.5, $-0.5, $6.5)
-
Y = g(x) = x - 1.5
-
확률변수함수(Z)의 기대값
E[Z] = E[g(x)]
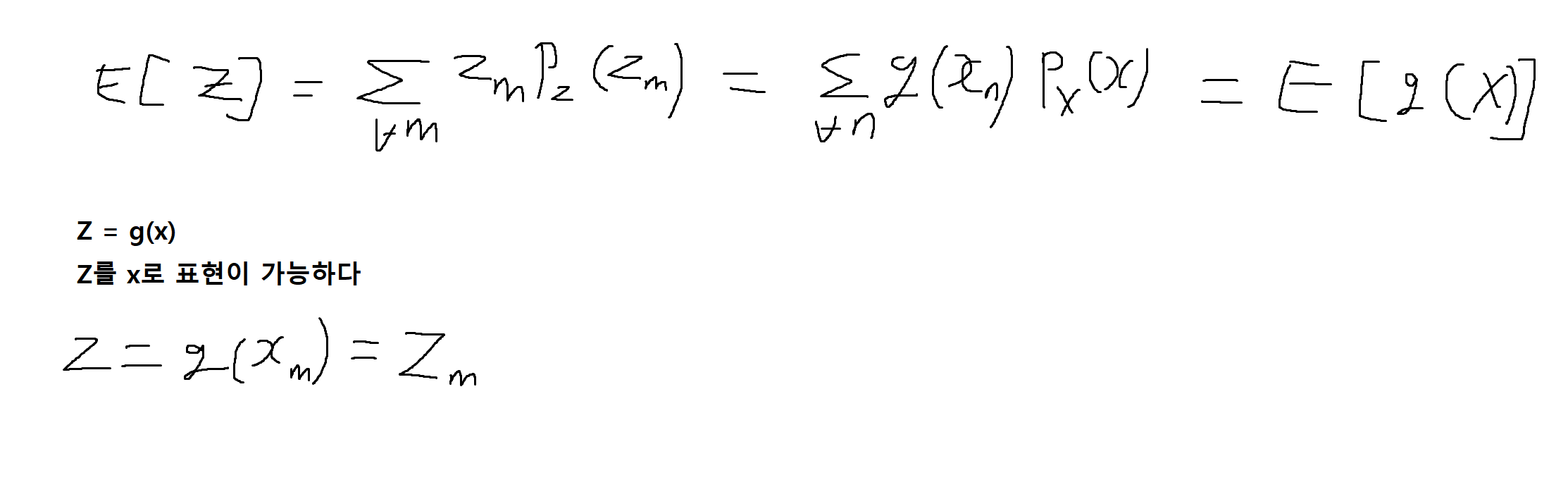
기대값, 분산, 표준편차 개념
평균 (기대값) : 주어진 수를 측정개수로 나눈 값으로, 대표값 중 하나
분산 : 변량들이 퍼져있는 정도, 분산이 크면 들죽날죽 불안정하다는 의미
표준변차 : 분산은 수치가 너무 커서, 제곱근으로 적당하게 줄인 값
기대값의 특성
(1) E[g(x) + h(x)] = E[g(x)] + E[h(x)]
(각각을 더해주면 된다)
(2) 상수 a,b에 대해, E[aX + B] = a * E[x] + b
(3) 상수 c, x = c, E[x] = X[c] = c
-> 확률변수 x가 상수값을 가지면 상수값 c로 나온다 (1개의 값만 가진다)
E[x] = c * 1 = 1
-
확률변수 X의 특성 : 확률변수 X 가질 수 있는 값, 그 확률의 분포 -> 확률분포
-
이산확률 변수에서는 확률질량함수(PMF) 이용
-
확률분포를 기대값, 모멘트 등으로 좀 더 세밀하게 구분할 수 있다.

- 확률변수 X에 분산은 상수 덧셈 / 뺄셈은 분산에 영향을 미치지 않는다.
-> Var[x] = Var[x+-7]
분산의 특성
(1) 상수 a, b에 대해, Var[aX] = a^2 * Var[X]
(2) 상수 c, X = c, Var[x] = Var[c] = 0
Var[X] = E[(x-mx)^2] = (c-c) = E[0] = 0
예제 3-11. 세 번의 동전던지기에서 앞면의 수가 2이면 $1을 받고, 그 수가 3이면 $8을 받지만 그외의 경우는 $0을 받는 게임이 있다. 게임 참가비가 $1.5이고 게임 참가로 얻을 수 있는 이익은 Y라 할 때, Y의 분산을 구하여라.
X => Sx = {0, 1, 8}
Px(0) = 1/2, Px(1) = 3/8, Px(8) = 1/8
Y = X - 1.5
Y => Sy = {-1.5, -0.5, 6.5}
Py(-1.5) = 1/2, Py(-0.5) = 3/8, Py(6.5) = 1/8
E[X] = 11 / 8
E[X²] = ∑x² P(x)
= (0² 1/2) + (1² 3/8) + (8² * 1/8) = 67 / 8
Var[Y] = Var[X] (분산은 상수 더하거나 빼는 것에 영향을 안받는다)
= 67/8 - (11/8)² = 415 / 65
예제 3-12. 성공확률이 p인 베르누이 확률변수 X의 분산을 구하여라
X = 1 (성공), 2(실패)
E[X] = 1 p + 0 (1-p) = p = mx
E[X²] = 1² p + 0² * (1-p) = p
Var[X] = E[X²] -mx² = p - p² = p(1-p)
요약
- 두 확륣사건의 독립조건
- 베르누이 시행, 순차실험
- 확률변수 : 이산확률변수
- 확률질량함수 (PMF)
- 이산확률변수의 기대값, 모멘트
