T/F 확인 복습문제
(1) 임의의 확률변수 X의 누적분포함수 (CDF) Fx(x)는 모든 x에서 연속이다.
-> F (범위에 따라 값이 정해진다)
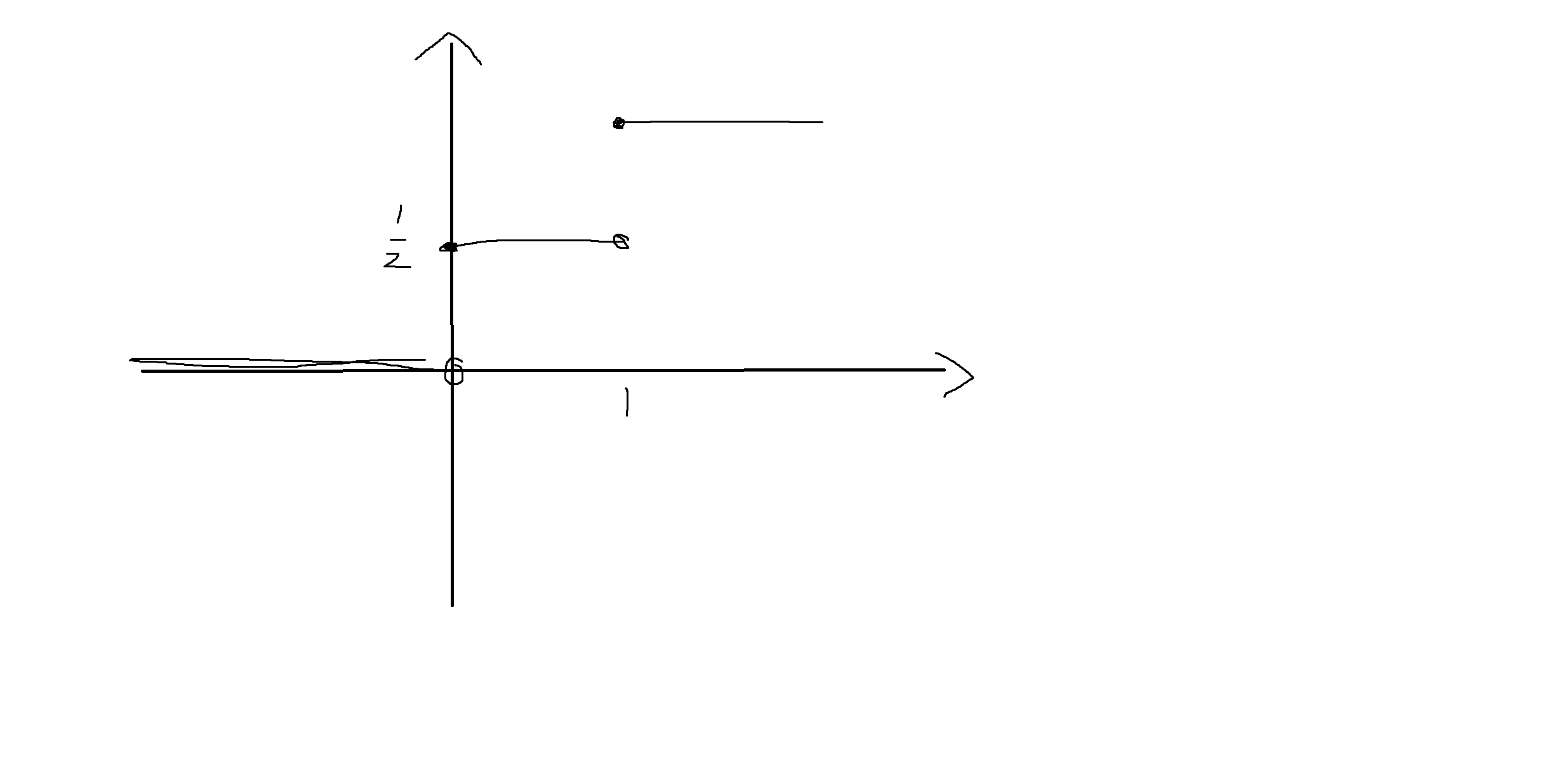
(2) 확률변수 X의 누적분포함수 (CDF) Fx(x)에 대해, Fx(b) < Fx(a)이면 a<=b이다.
-> F
a<=b -> Fx(a) <= Fx(b) (p -> q)
p -> q == ~q -> ~p (대우)
Fx(a) > Fx(b) -> a > b
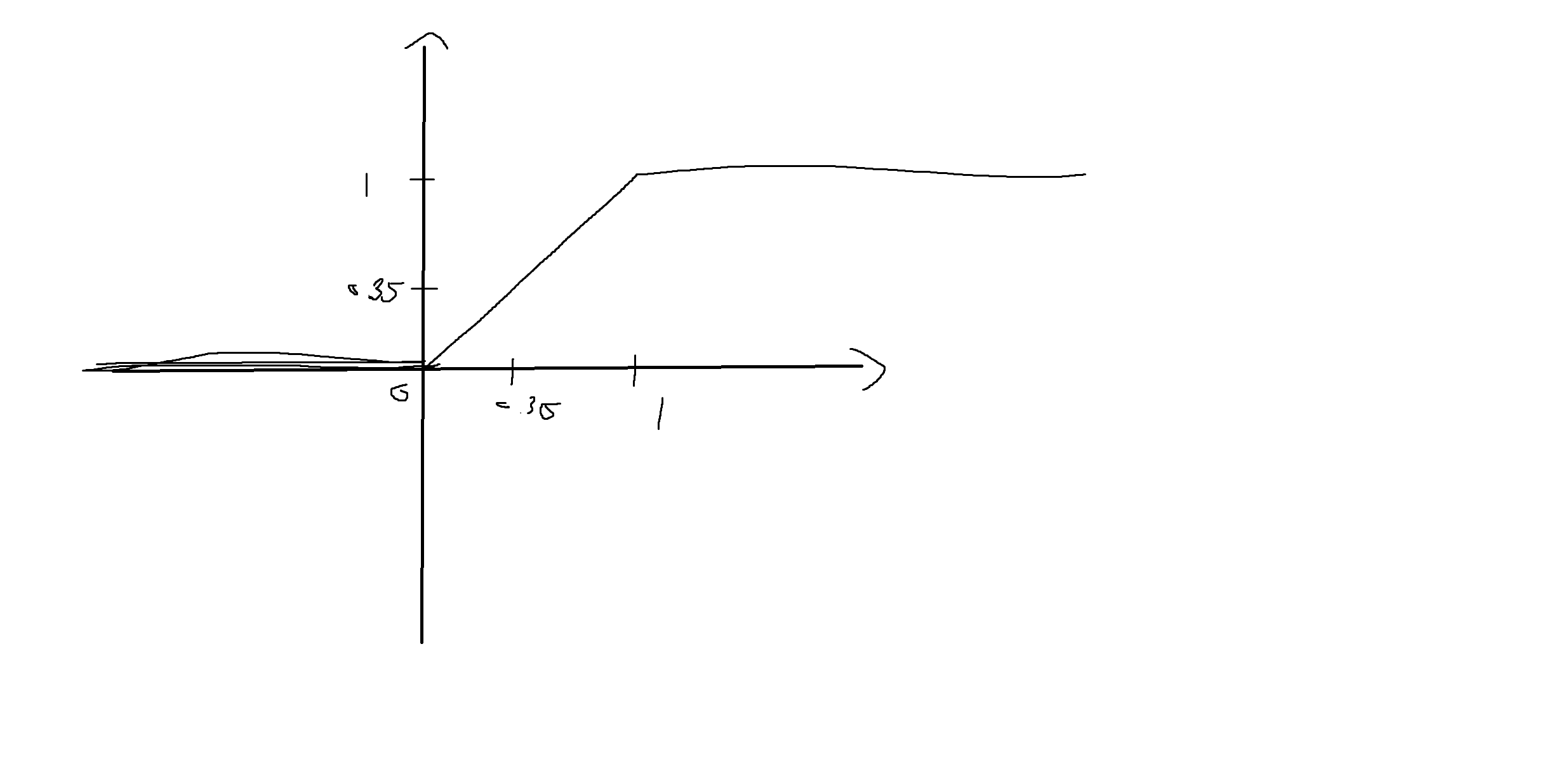
(3) 0과 1사이에서 정의된 균등확률변수 X의 P[|X| < 0.35]의 값은 0.70이다.
P[-0.35 < X < 0.35] = Fx(0.35) - Fx(-0.35) = 0.35 - 0 = 0.35
확률밀도함수
- 우리의 관심 : 확률변수 X의 특성
| 이산확률변수 | 연속확률변수 |
|---|---|
| PMF(확률질량함수) Px(x) = P[X=x] | CDF(누적분포함수) Fx(x) = P[X<=x], PDF(확률밀도함수) fx(x) = d/dx Fx(x) |
| 기대값, 분산 -> summation 형태 ∑ | 기대값, 분산 -> integral 형태 ∫ |
| 베르누이/이항/기하/포아송 RVS |
확률밀도함수 (PDF : Probability density function) : 확률변수 X의 누적분포 함수 (CDF) Fx(x)를 x에 대해 미분한 함수
fx(x) = d/dx Fx(x)
-> 확률변수 X의 특정점 x에서의 확률의 "밀도" 값(!= 확률)을 나타냄)
(밀도 = 특정값에서의 값이 얼마나 의미가 있나)
- 확률밀도함수(PDF)의 특성 (* 확률변수 X)
(1) fx(x) >= 0
(2) P[a <= X <= b] = ∫a to b fx(x) dx -> 해당 범위의 값을 적분한 값
(3) Fx(x) = ∫-∞ to x fx(t) dt -> (PDF를 적분하면 CDF가 된다)
(4) ∫-∞ to ∞ fx(x) dx = 1 -> (전 구간 계산 합 -> 확률값 1)
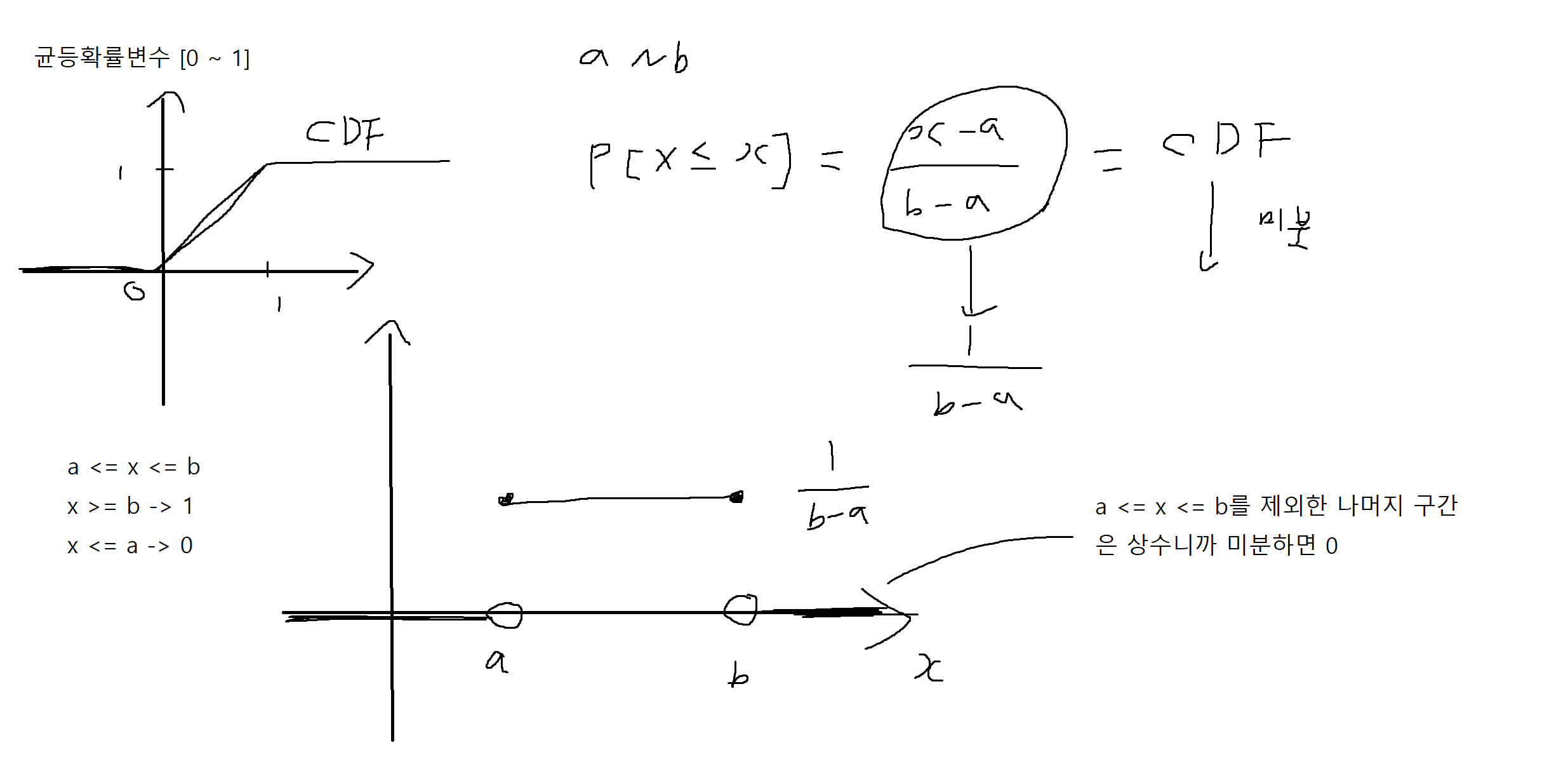
예제 4-6 : X가 a와 b사이에서 정의된 균등확률변수일 때, PDF를 구하여라
예제 4-7 : 통신시스템의 메시지 전송시간은 연속확률변수 X로 모델린되어 X는 지수분포에 따르며, 전송시간이 특정시간 x보다 클 확률은 다음과 같이 정의된다. 이때, X의 CDF와 PDF를 구하여라.
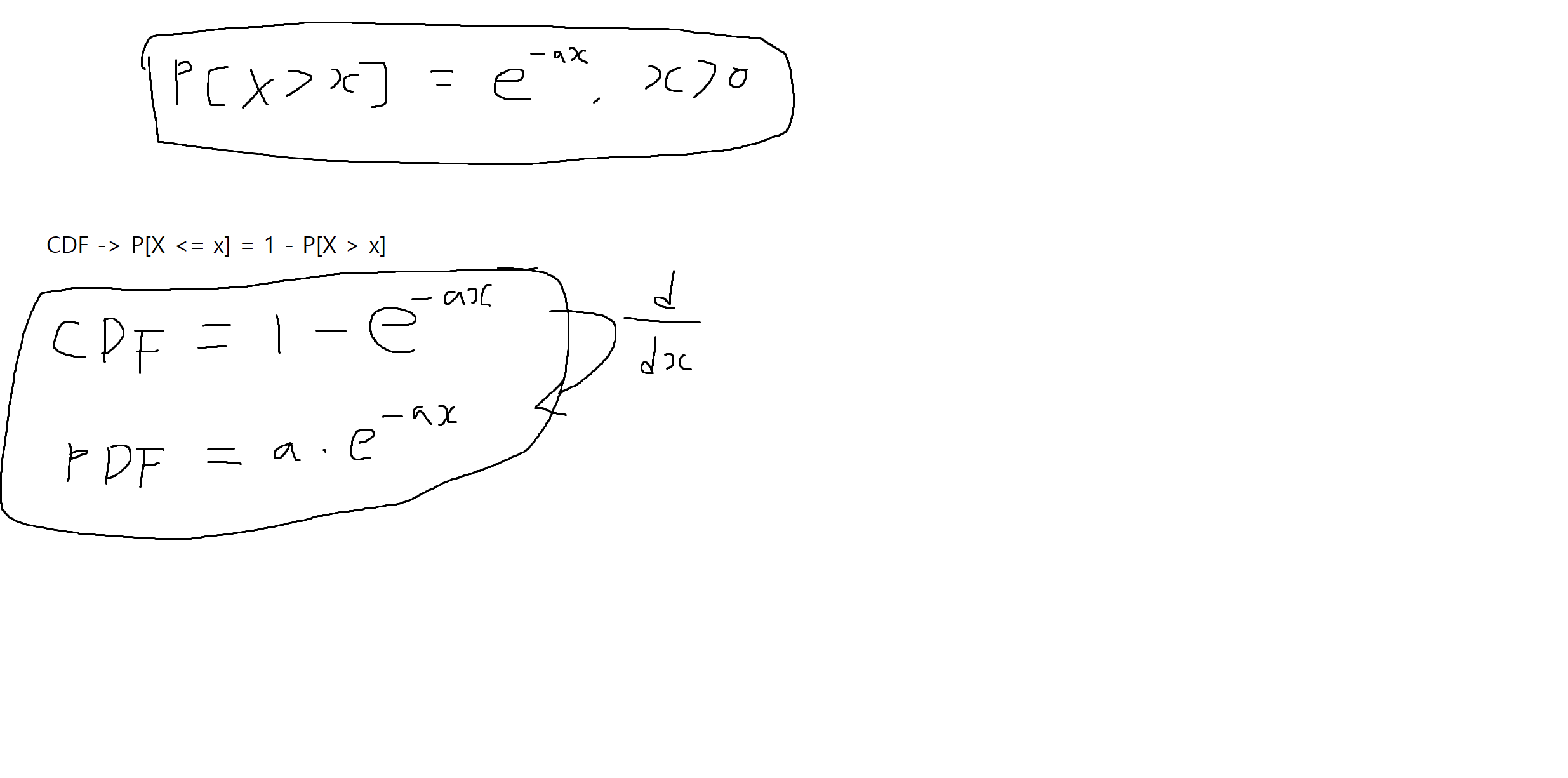
-
이산확률변수의 PDF
CDF : 일반적인(이산 / 연속) 확률변수에서 구간을 포함하는 사건의 확률표시
PDF : 특정 점 (X = x)에서 확률의 밀도를 표시, PMF와 유사하지만 다른 의미 -
이산확률변수의 PDF 표현
이산확률변수의 CDF 표현 : 단위계단함수 (unit step function) 사용
단위 계단함수 (unit step function)와 델타함수 (delta function)의 관계 이용 -
단위 계단함수 (unit step function) :
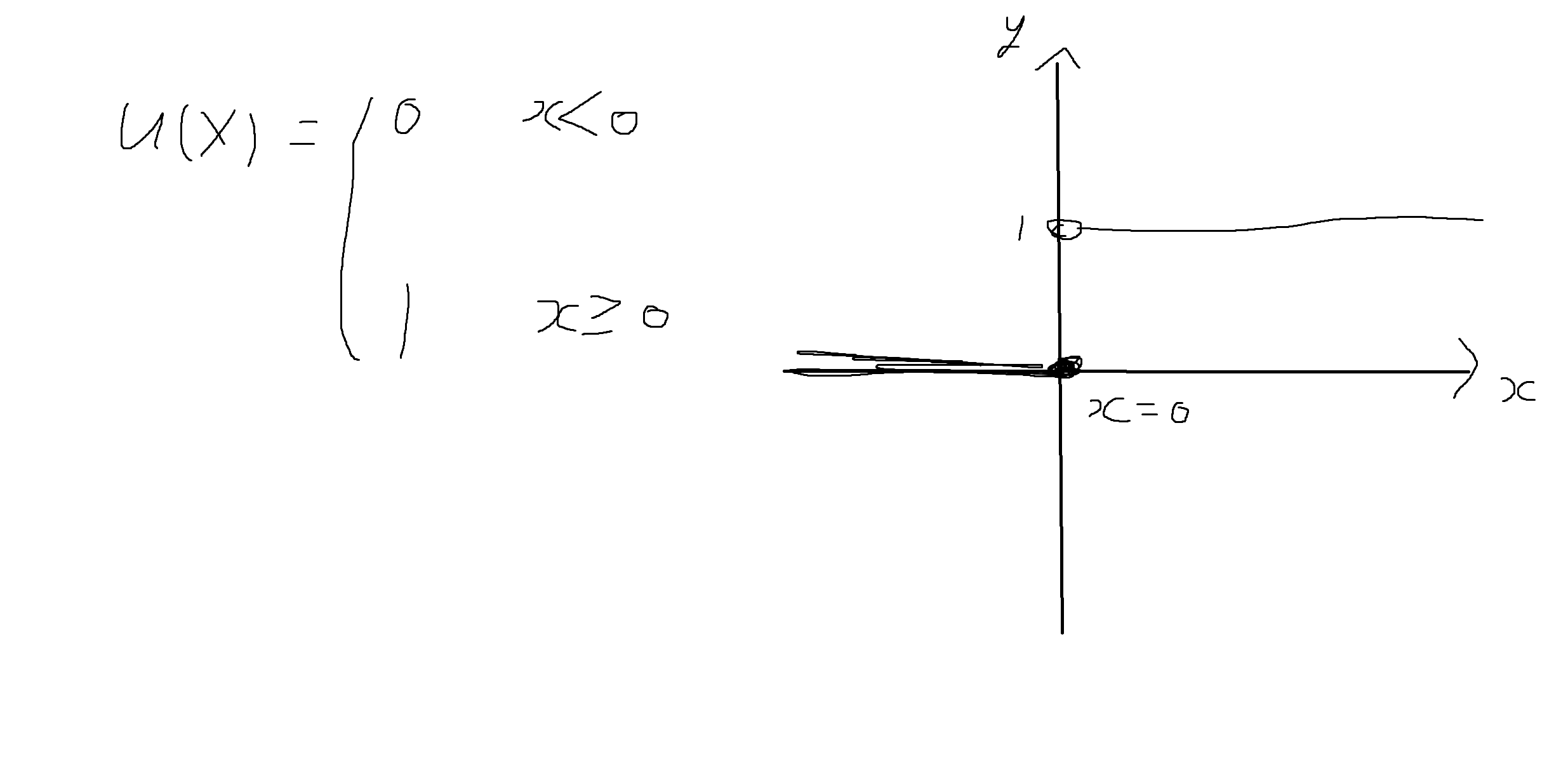
-
델타 함수 (delta function):
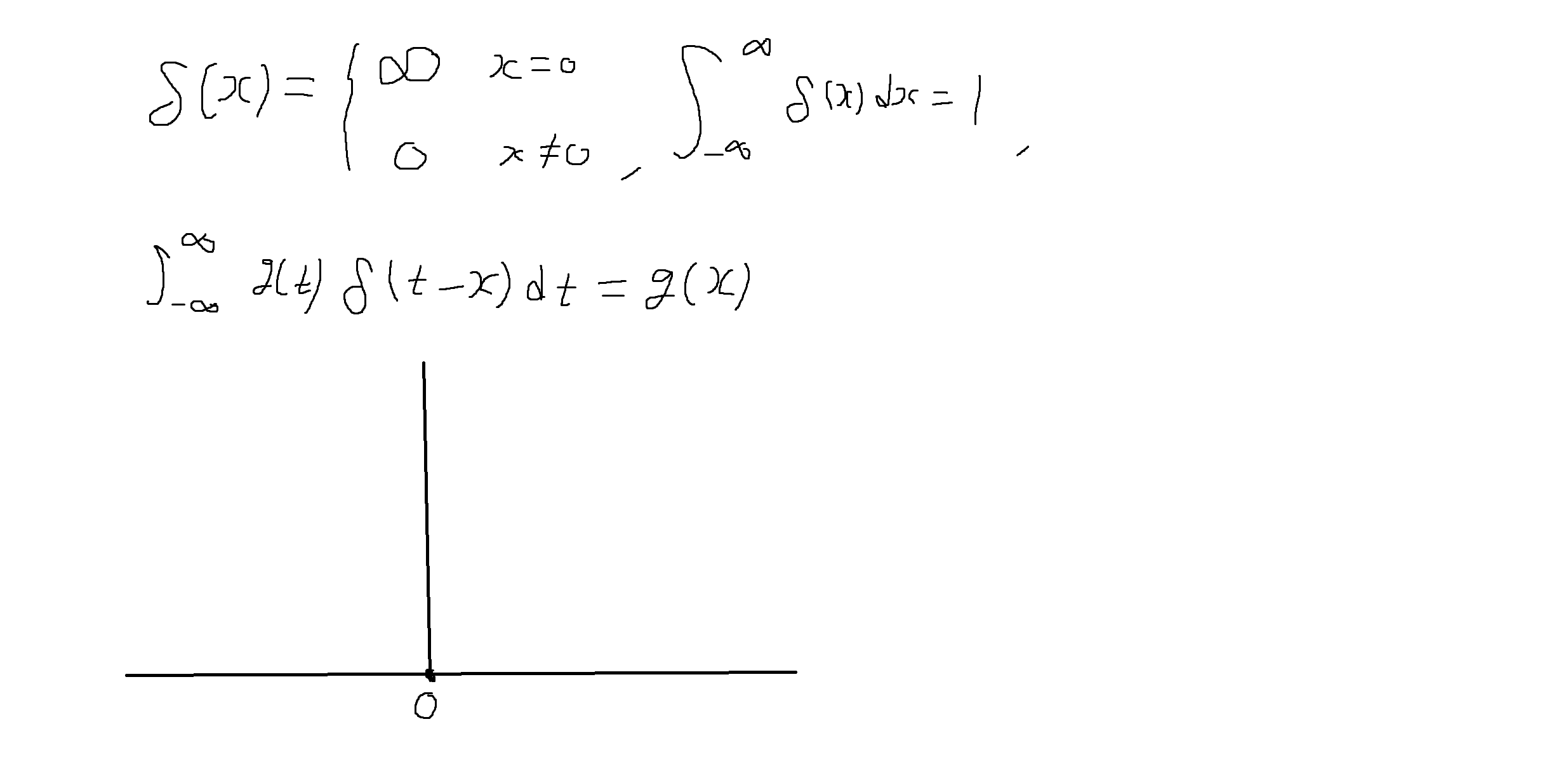
- 우리의 관심

예제 4-8 : 동전을 세번 던져서 나온 앞면의 수를 확률변수 X의 CDF와 PDF를 단위계단함수 u(x)와 델타함수 δ(x)를 이용하여 나타내어라.
PMF -> Px(0) = 1/8, Px(1) = 3/8, Px(2) = 3/8, Px(3) = 1/8
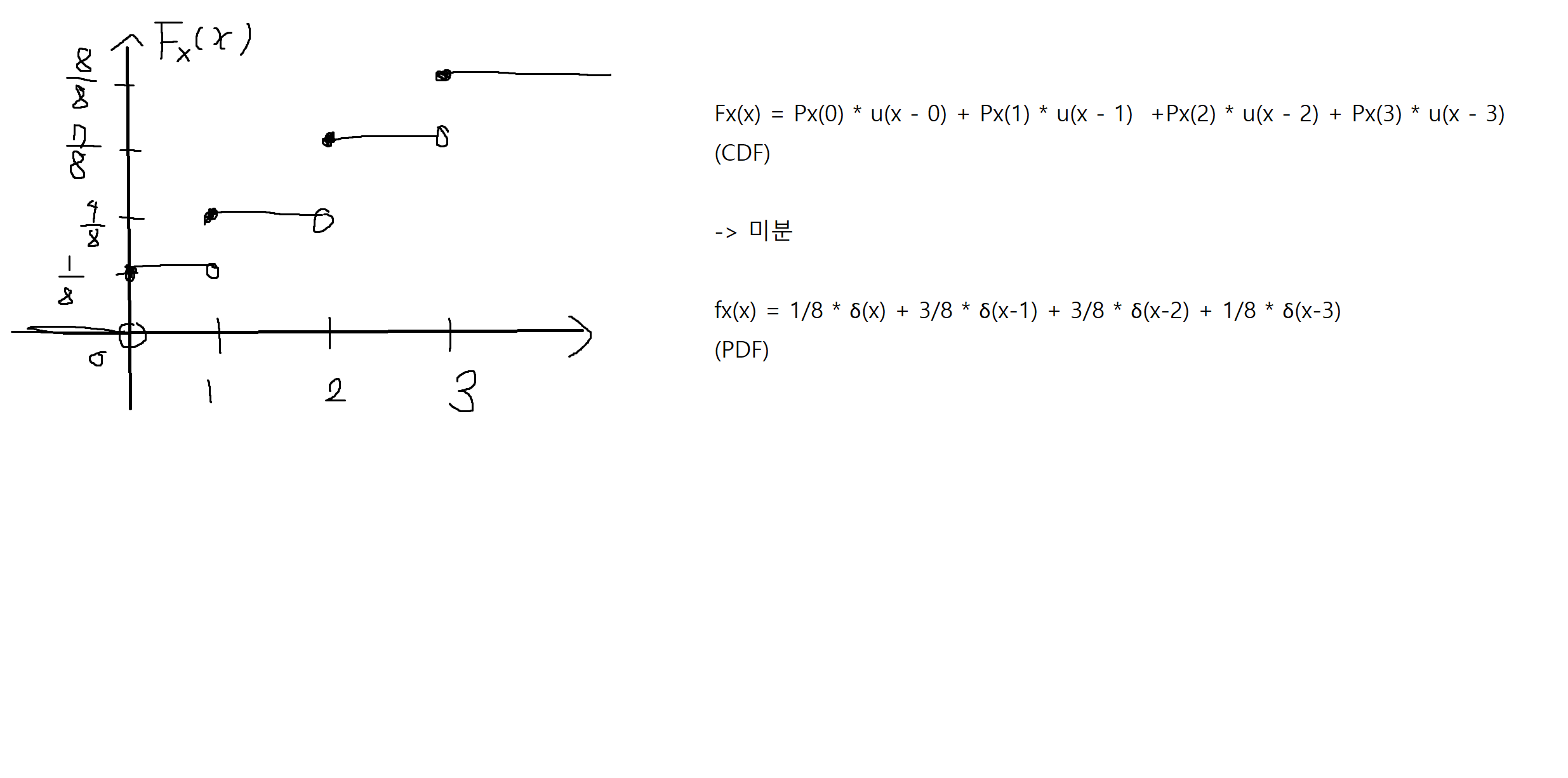
예제 4-9 : 동전을 세 번 던져서 나온 앞면의 수를 확률변수 X라고 할 때, 사건 A = {1 < x <= 2}, B = {2 <= x < 3}의 확률을 X의 PDF를 적분하는 방법으로 구하여라
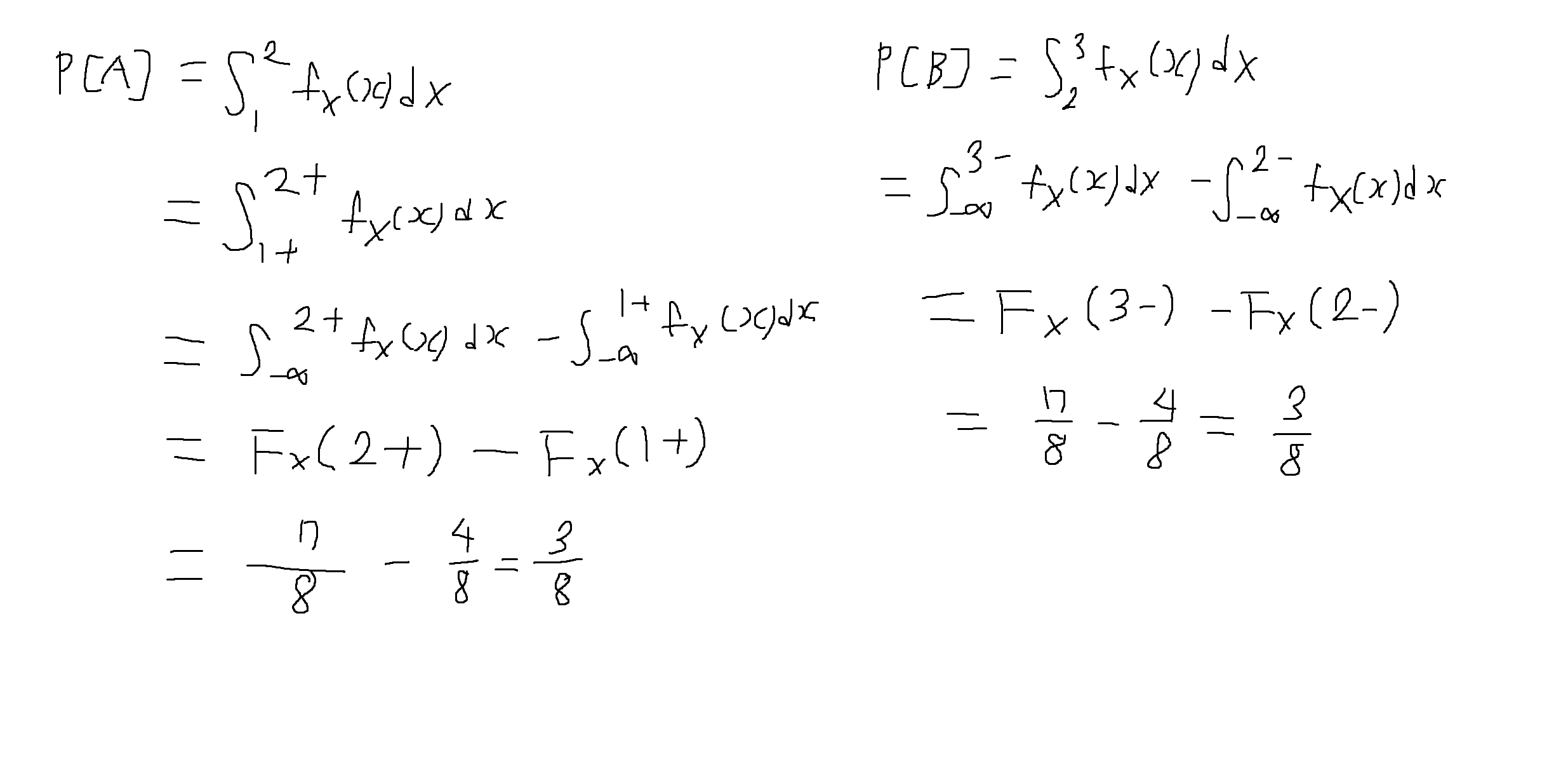
- 조건부 CDF와 PDF (확률변수 X) : 조건부 PMF의 경우와 마찬가지로 특정 사건 C에 대한 정보가 주어졌을 때 X의 CDF와 PDF는 다음과 같이 정의
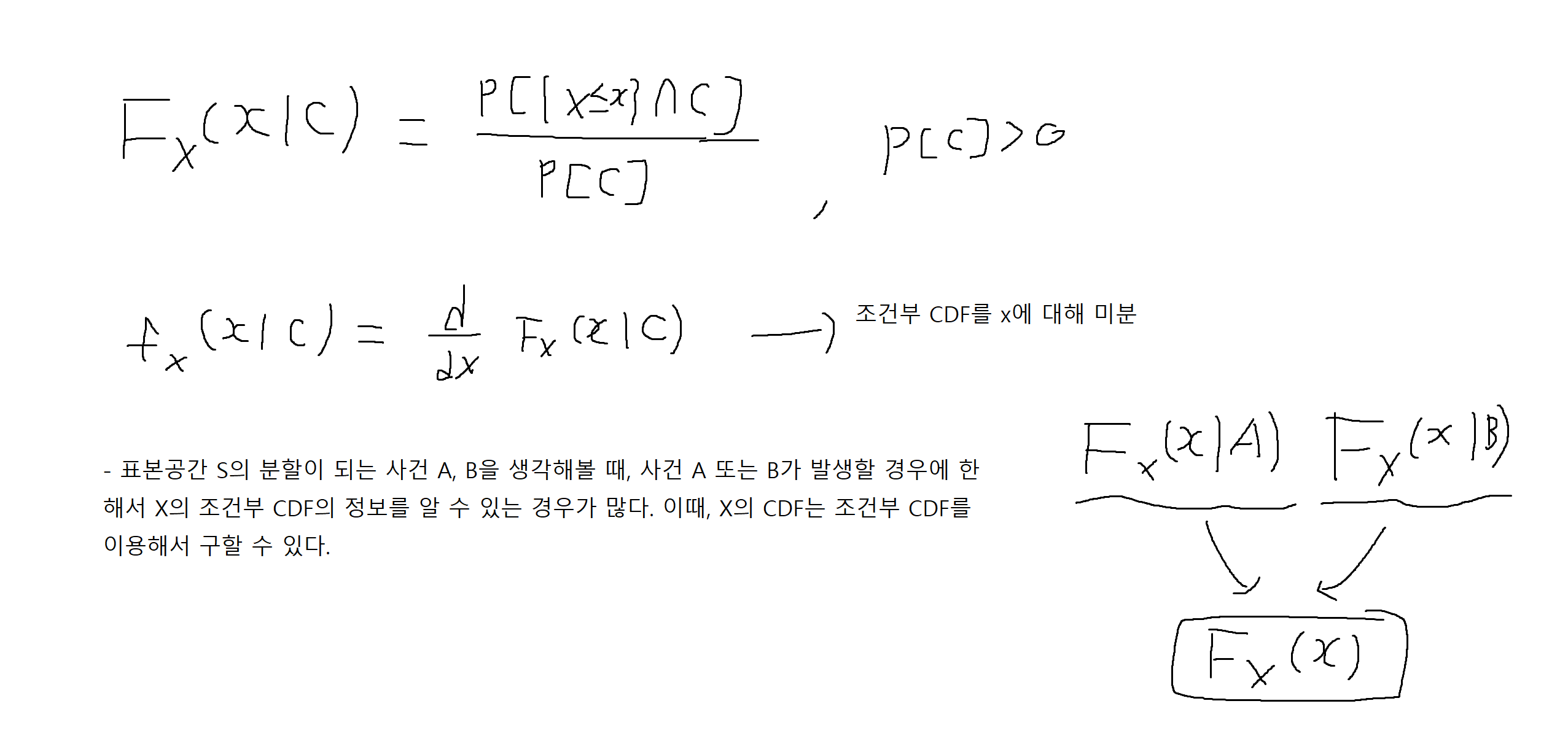
예제 4-10 : 어떤 기계의 수명 X는 연속 CDF Fx(x)를 갖는다. 사건 c = {X > t}가 (t는 상수) 주어진 조건부 CDF와 조건부 PDF를 구하여라.
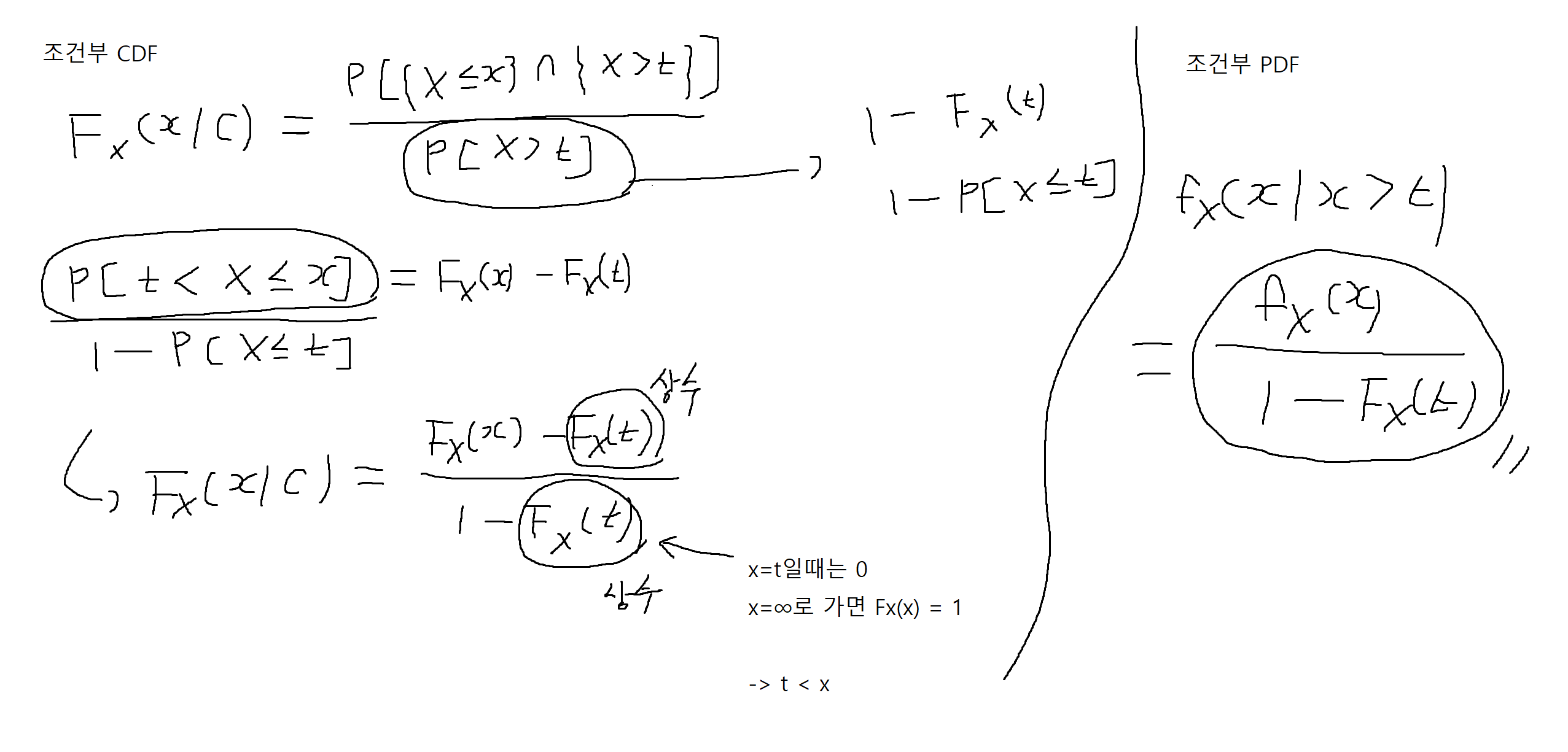
예제 4-11 : 확률변수 X는 다음과 같은 PDF를 갖는다.
fx(x) = c * (1 - x^4) (if -1 <= x <= 1)
= 0 (otherwise)
(1) c를 구하여라
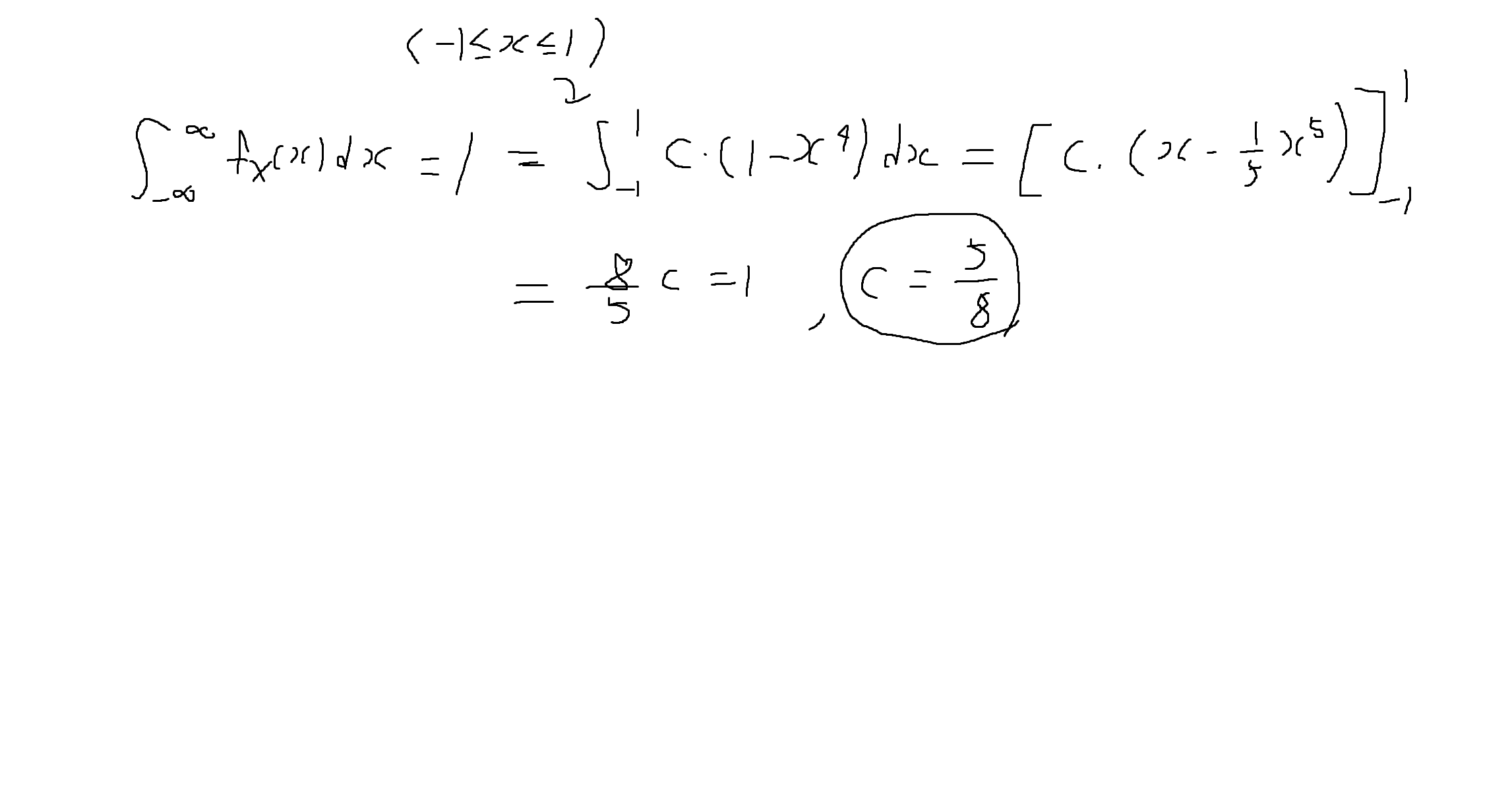
(2) X의 CDF를 구하여라
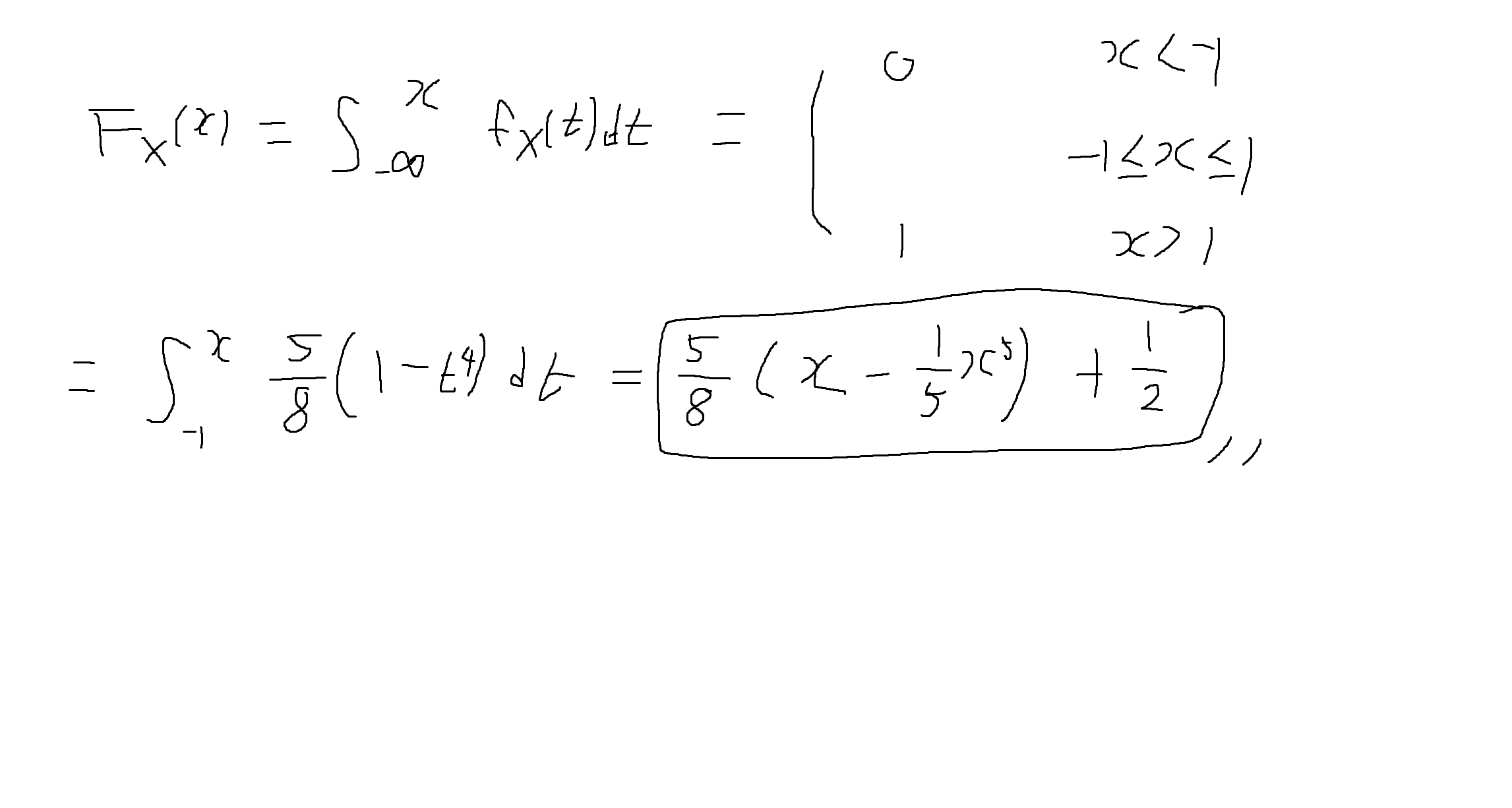
(3) P[|x| < 1/2]를 구하여라
-> 같은 방식으로 계산하면 79 / 128이 나옴
예제 4-12 : 어떤 다트는 반경이 4인 원형의 과녁안의 모든 지점에 균등하게 떨어진다. 원점으로부터 떨어진 지점까지의 거리를 R이라고 할 때, 다음을 구하여라.
(1) R의 CDF를 구하여라.
P[R <= r] = 관심면적 / 전체면적 = πr² / π4²
= r²/16 (0 <= r <= 4)
= 1 (r > 4)
= 0 (r < 0)
(2) FR(r | R>1)와 fR(r | R>1)을 구하여라
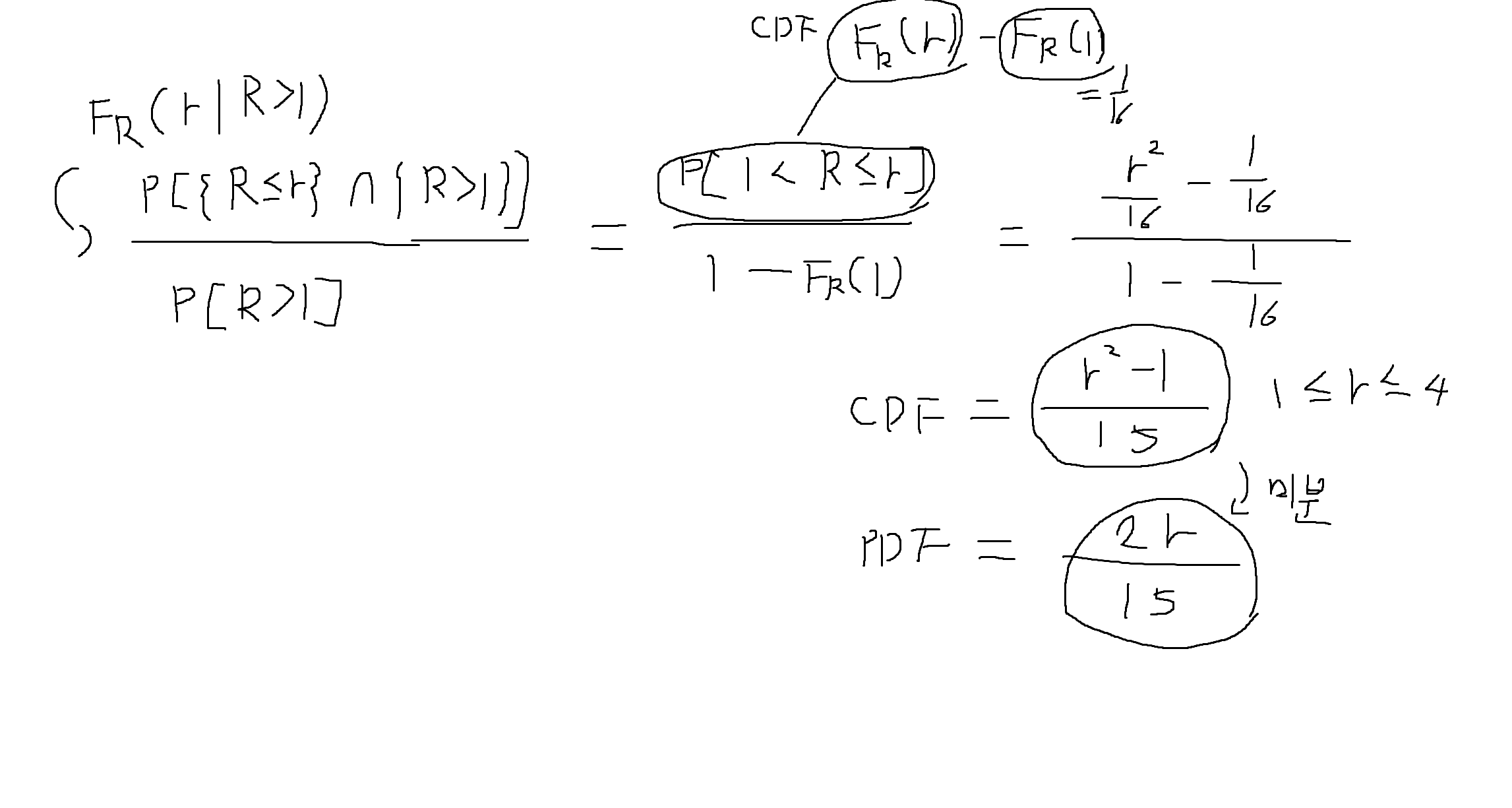

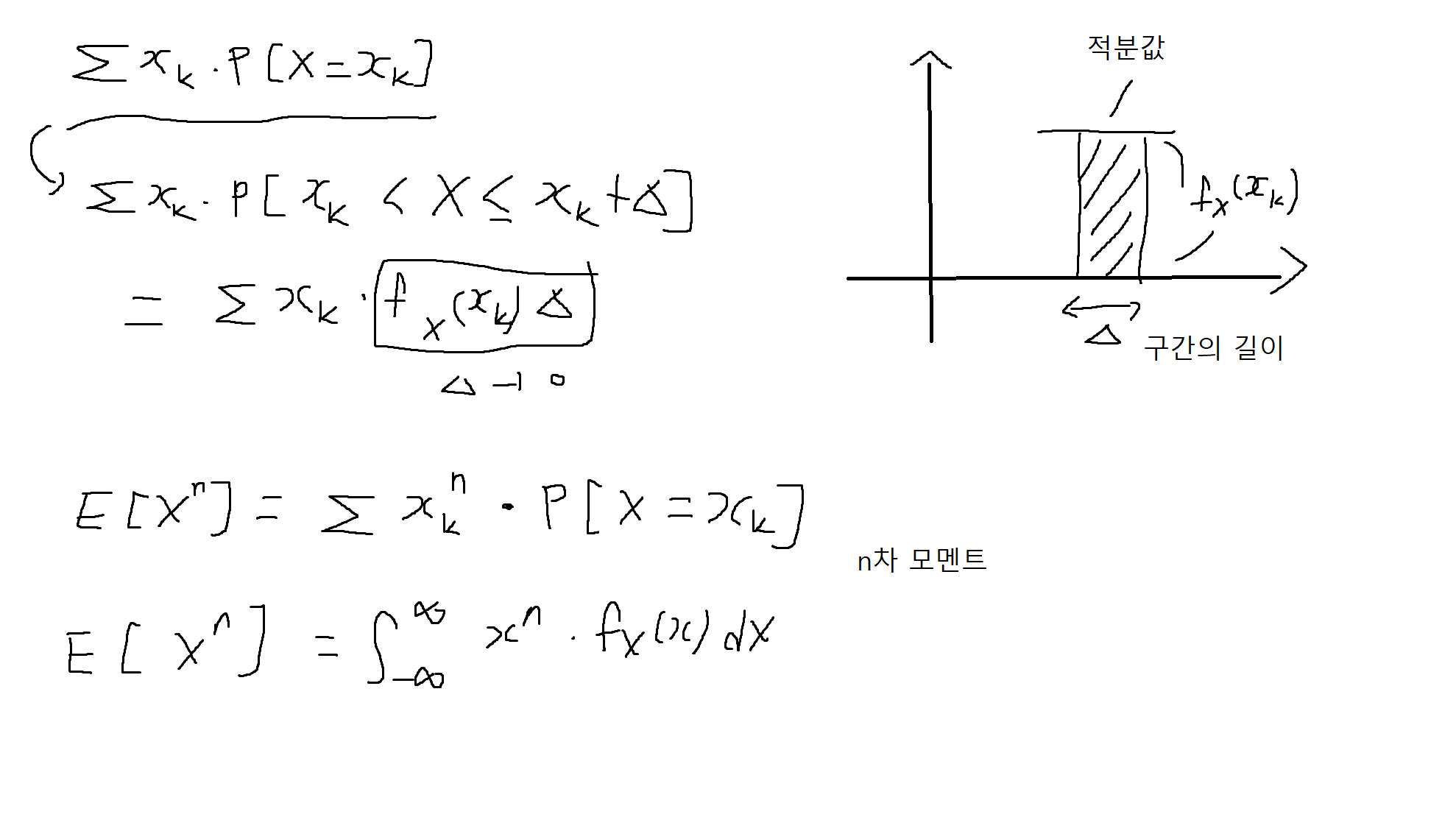
- 특정확률변수(Y)가 다른 확률변수(X)의 함수로 주어졌을 때 기대값 E[Y]
-> E[Y]는 Y = g(X)일 때, X의 PDF와 g(x)를 이용하여 계산가능

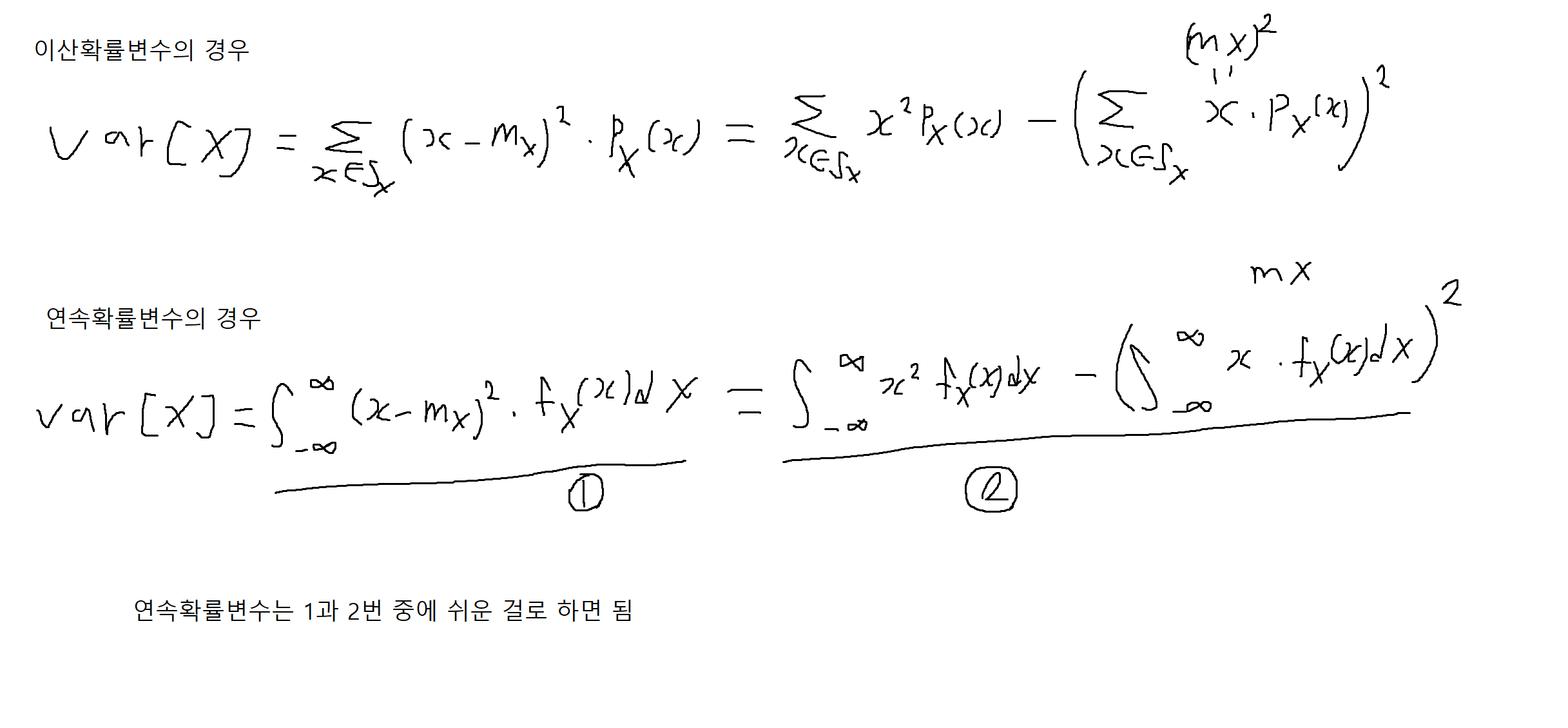
- 확률변수 X의 분산
Var[X] = E[(X-mx)²] = E[X²] - mx²
예제 4-13 : 연속확률변수 X는 구간 [a,b]에서 균등하게 분포할 때 (즉, 균등확률변수), X의 기대값과 분산을 구하여라.
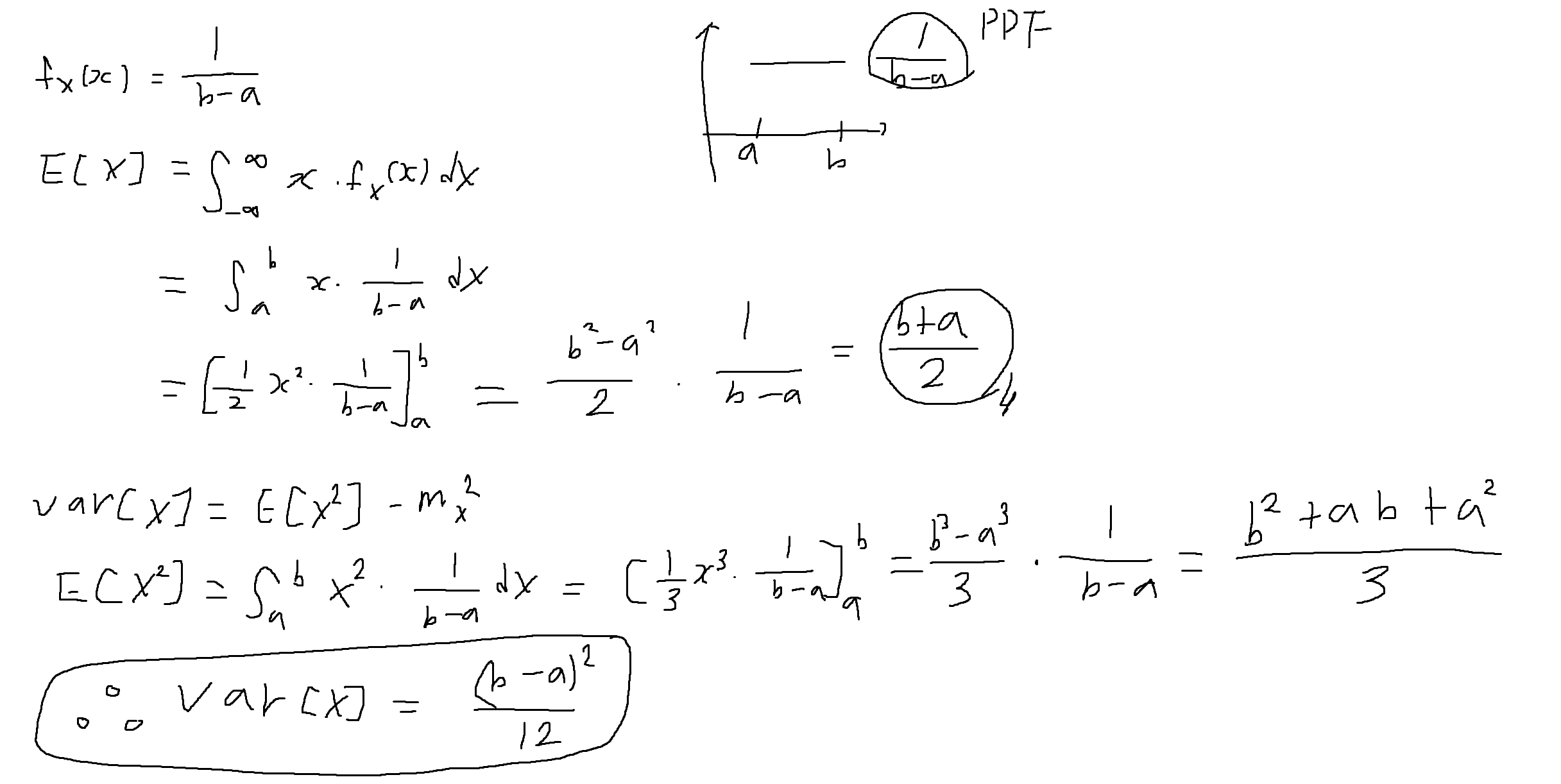
예제 4-14 : 어떤 다트는 반경이 R0인 원형의 과녁안의 모든 지점에 균등하게 떨어진다. 원점으로부터 떨어진 지점까지의 거리를 확률변수 R이라고 할 때, R의 기대값과 분산을 구하여라
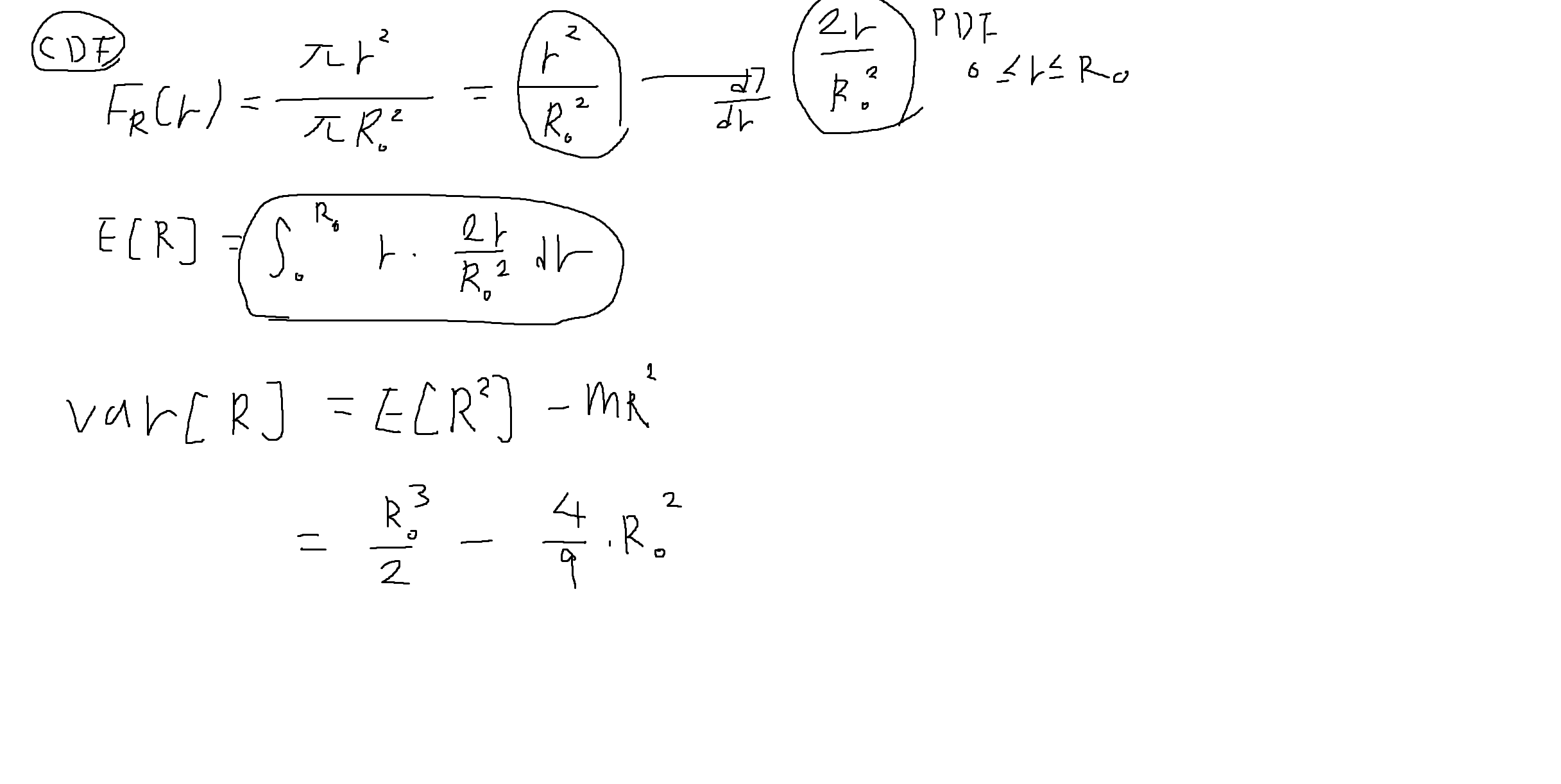
예제 4-15 : X가 연속이고 음수가 아닌 값만을 가질 때 (X >= 0), 다음을 증명하여라.
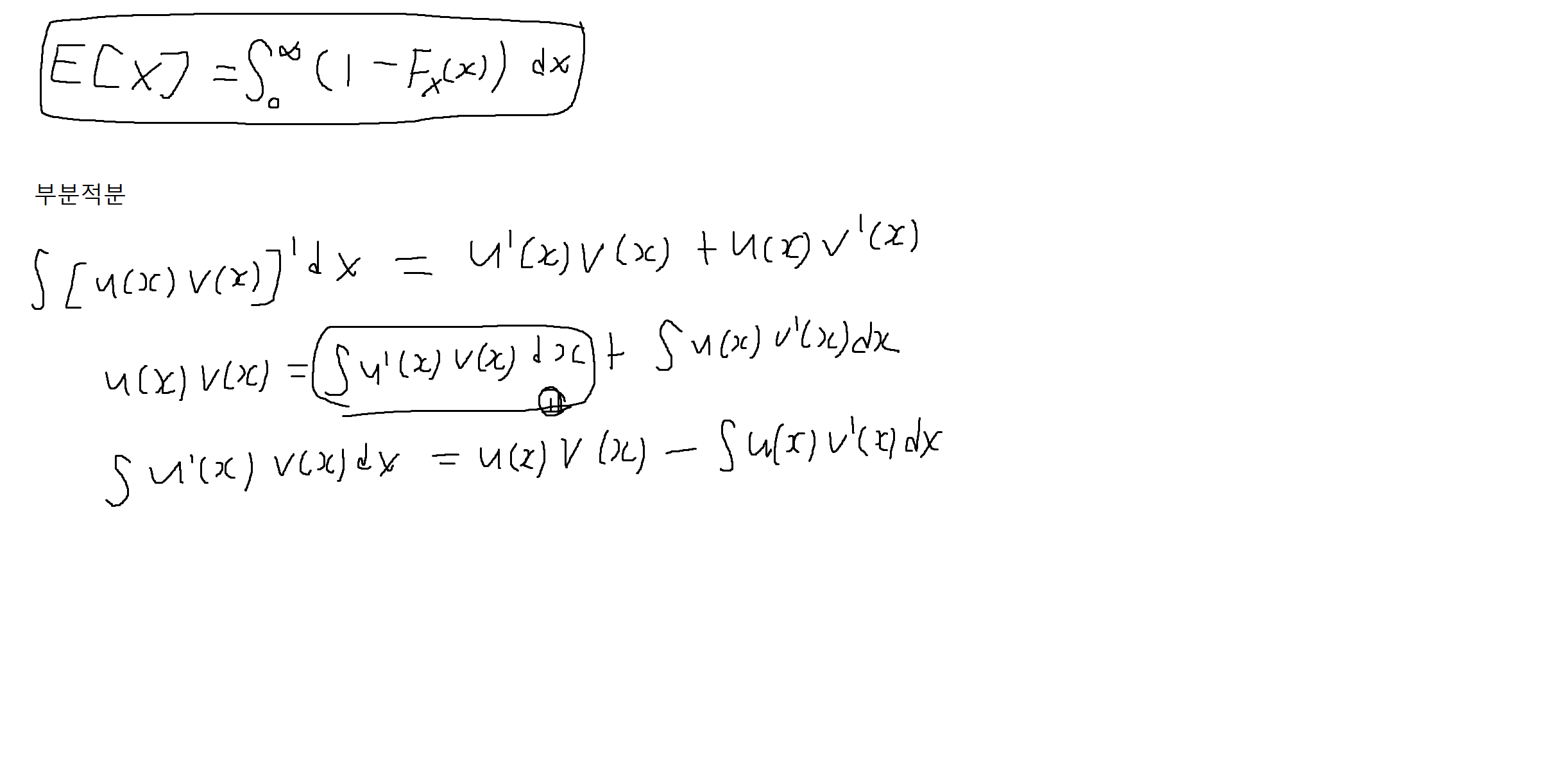
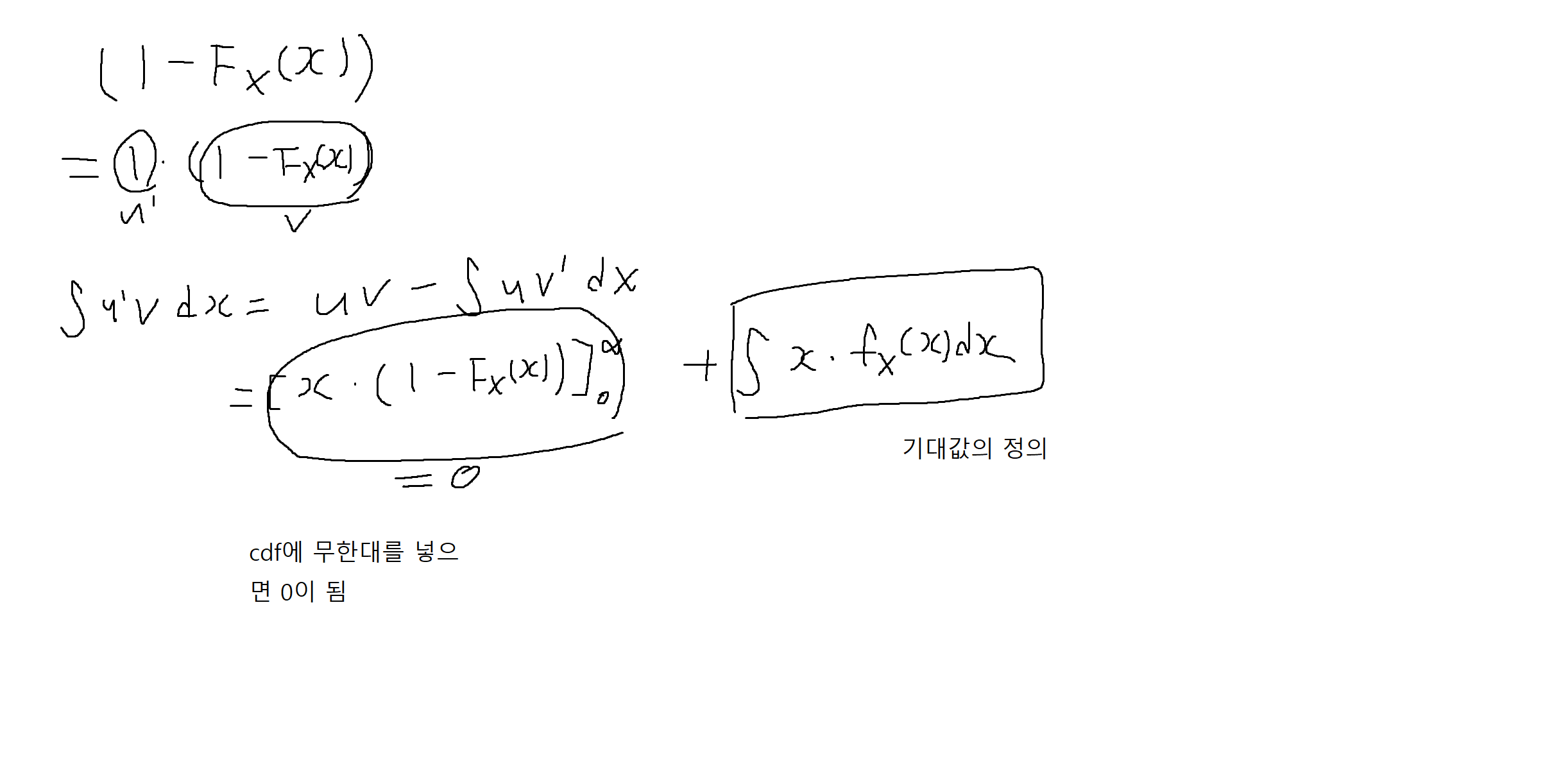


잘봤습니다. 좋은 글 감사합니다.