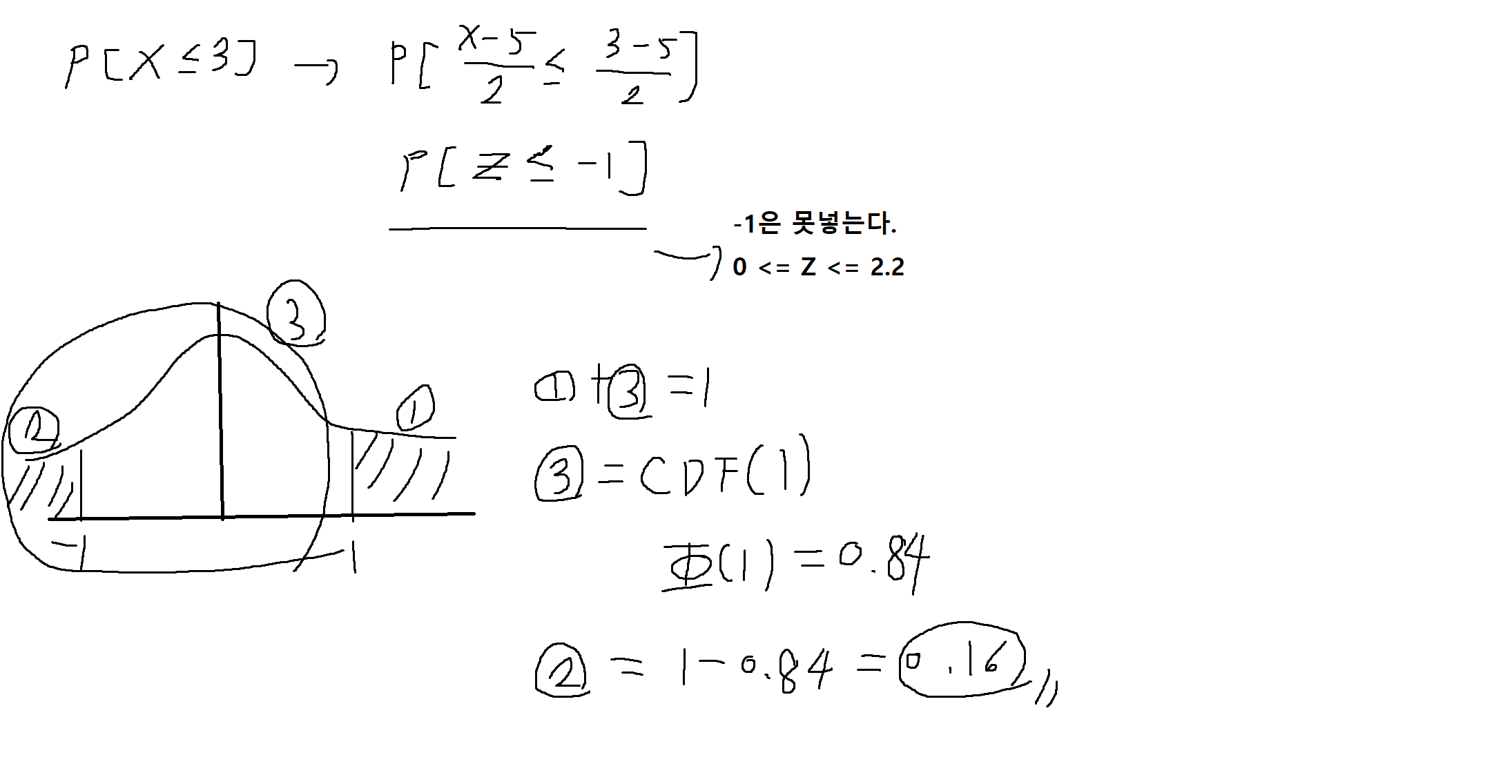복습
1. 확률변수 : 확률밀도함수 (PDF)
2. 기대값과 분산의 계산
- Integral 형태의 수식으로 표현
T/F 확인
(1) 임의의 확률변수 X의 확률밀도함수(PDF)를 fx(x)라고 할 때, fx(a)는 P[X=a]와 동일한 의미이다.
-> F
fx(a) (PDF)는 x=a일 때의 확률밀도.
(2) 연속확률변수 X가 구간 [-2, 2]에서 정의된 균등(uniform) 확률 변수이면, Var[X] = E[X²]이다.
-> T
- 우리의 관심 : 확률변수 X의 특성
| 이산확률변수 | 연속확률변수 |
|---|---|
| PMF(확률질량함수) Px(x) = P[X=x] | CDF(누적분포함수) Fx(x) = P[X<=x], PDF(확률밀도함수) fx(x) = d/dx Fx(x) |
| 기대값, 분산 -> ∑ 형태 | 기대값, 분산 -> ∫ 형태 |
| 베르누이/이항/기하/포아송 RVS | 연속확률변수에서는? |
-
이산확률변수에서와 마찬가지로 주요 확률변수의 특징을 학습
-> 공학문제를 보다 쉽고 다양한 방법으로 접근할 수 있음 -
세가지 확률변수를 학습 : 균등/지수/가우스 확률변수
-> 확률변수의 특징 : PDF(또는 CDF), 평균, 분산 등
균등확률변수 / 지수확률변수 / 가우스확률변수(정규분포)
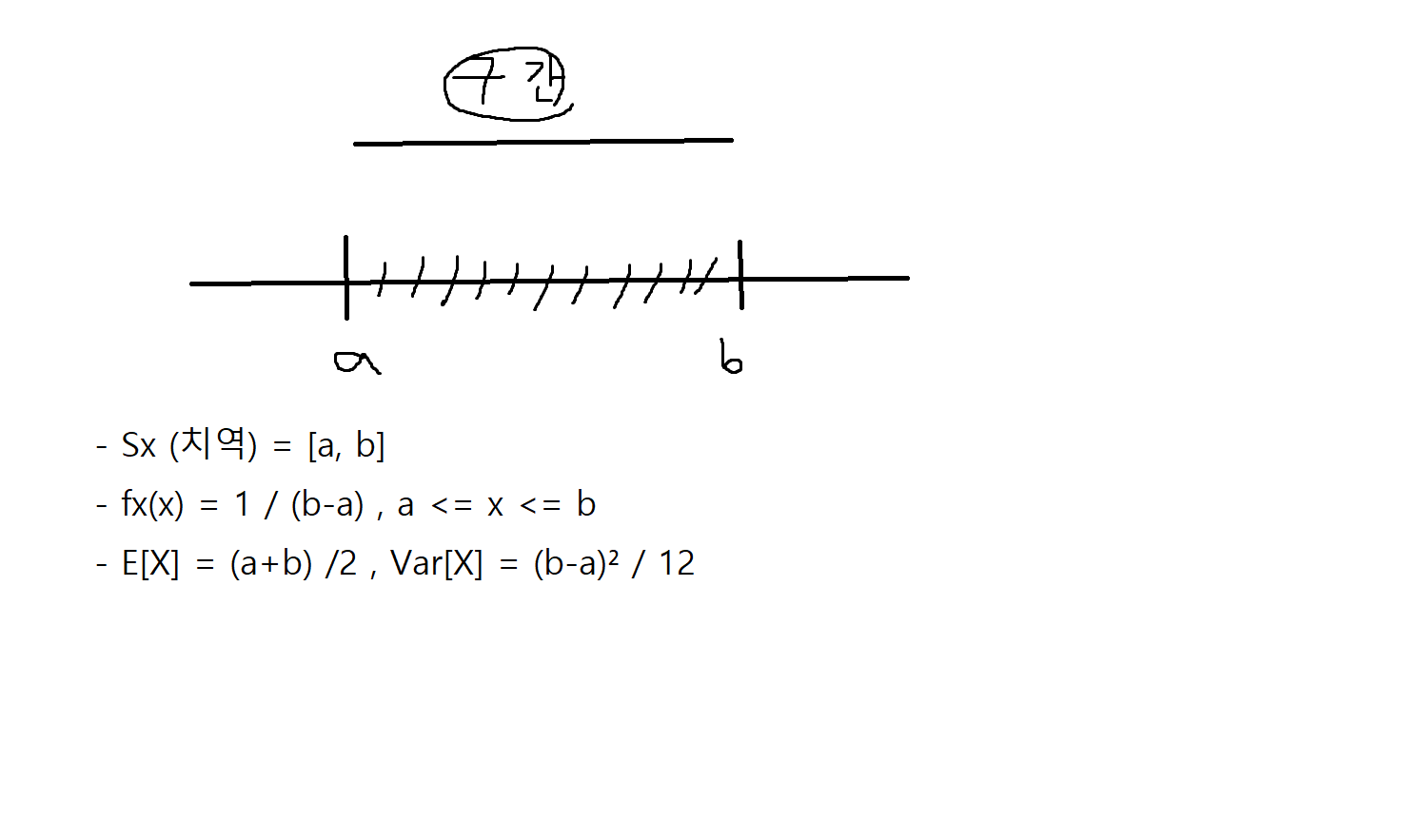
균등확률변수 (uniform random variable)
- 균등확률변수 X는 구간 [a,b]에서 균등하게 분포
지수확률변수 (exponential random variable)
- 지수확률변수 X는 특정대기시간을 모델링할 때 자주 쓰임
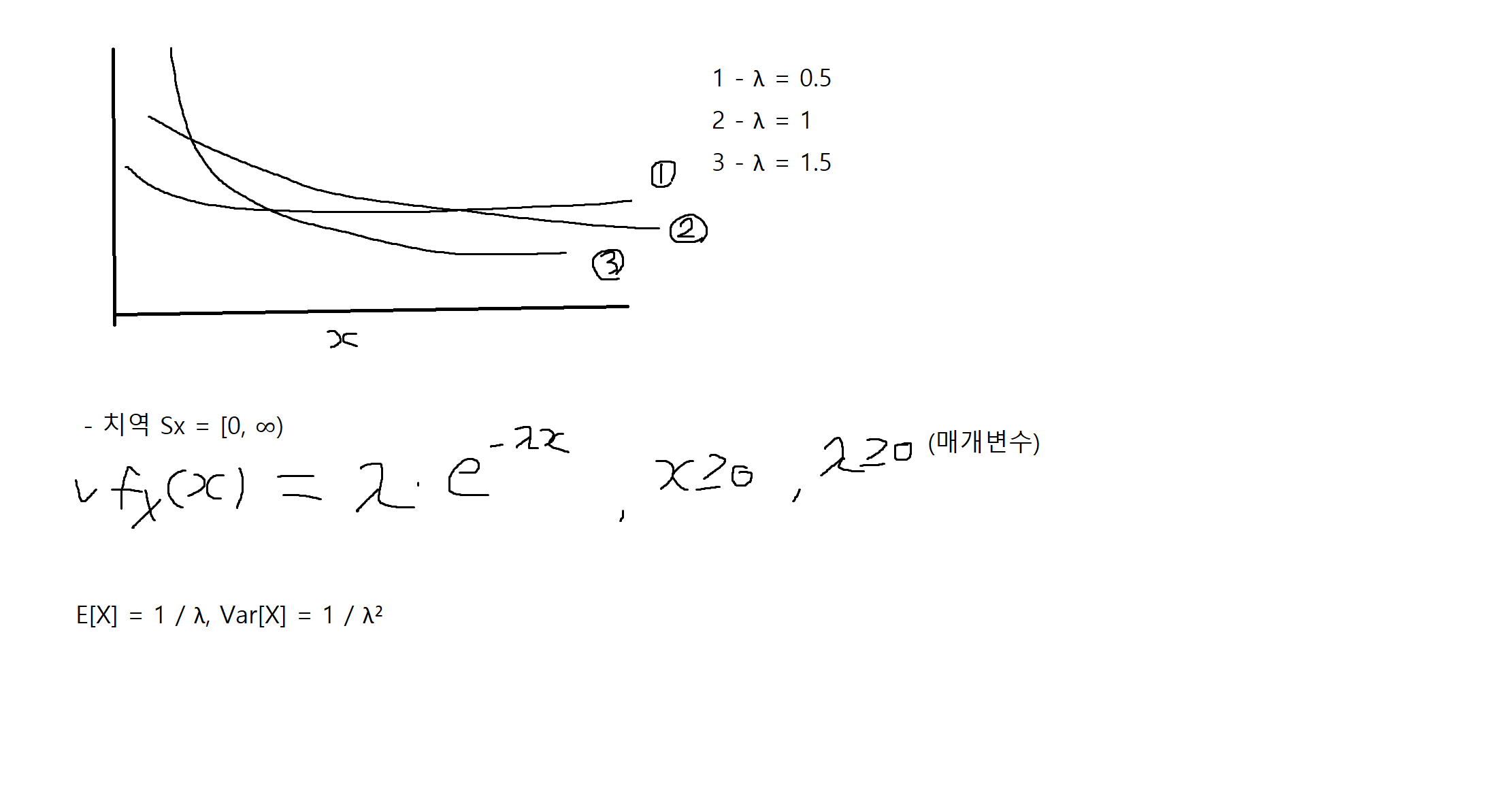
예제 4-16: 확률변수 X가 λ>0을 매개변수로 가지는 지수확률변수 일 때, X의 기대값과 분산을 구하여라
E[X] = 1/λ, Var[X] = 1 / λ²
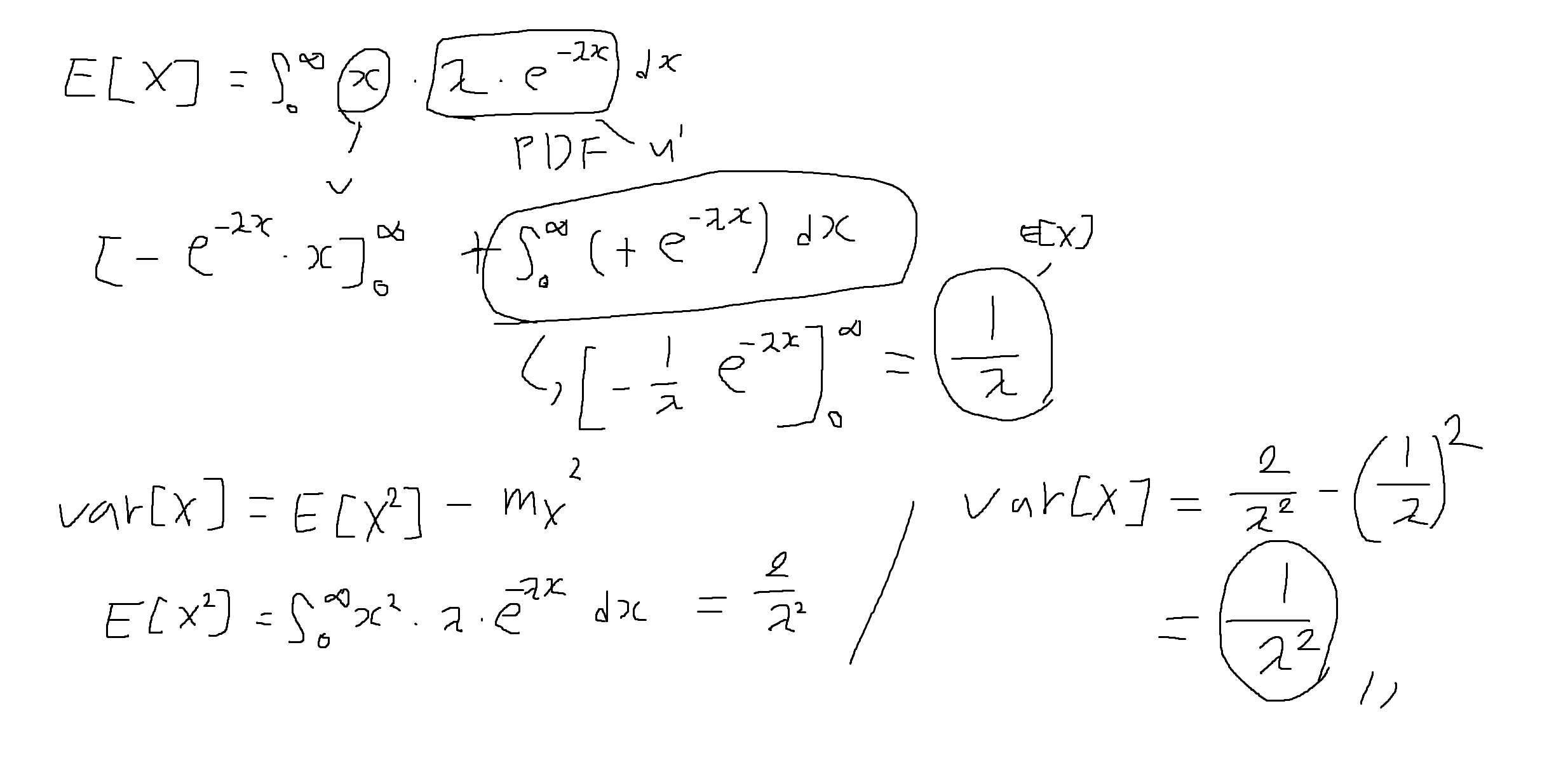
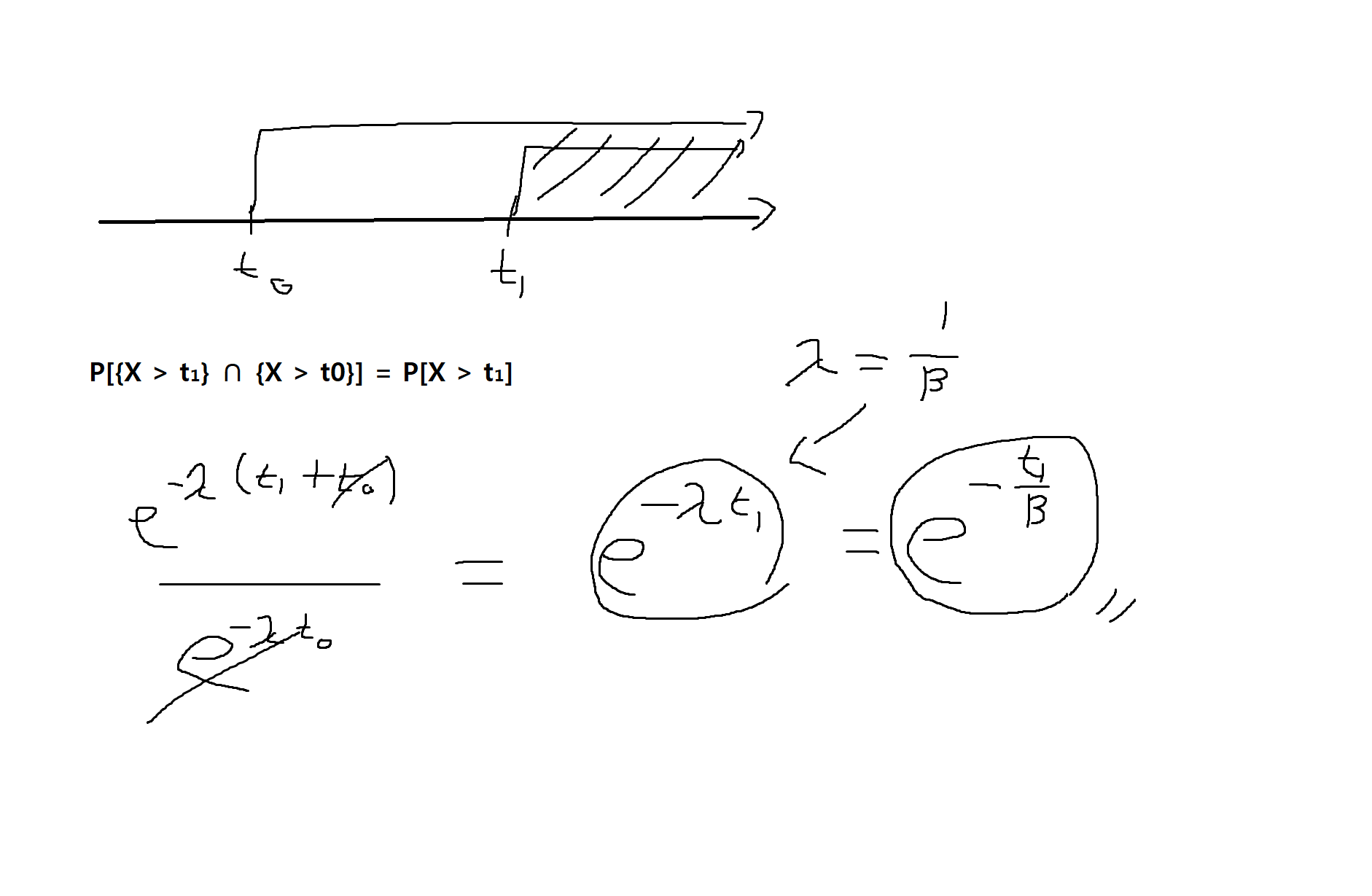
예제 4-17: 택시승강장에서 택시를 (처음부터) 기다리는 시간은 확률변수 X라고 하자. X가 지수확률변수이고 택시를 탑승하기 위한 평균대기시간이 B라고 할 때, 다음을 구하여라
(1) 어떤 승객의 탑승시간이 t₁보다 길어질 확률

(2) 어떤 승객이 이미 t0이라는 시간을 기다렸을 때, 탑승을 위해 추가로 기다려야 하는 시간이 t₁보다 클 확률
P[X > t₁| X > t0] = P[{X > t₁} ∩ {X > t0}] / P[X > t0]
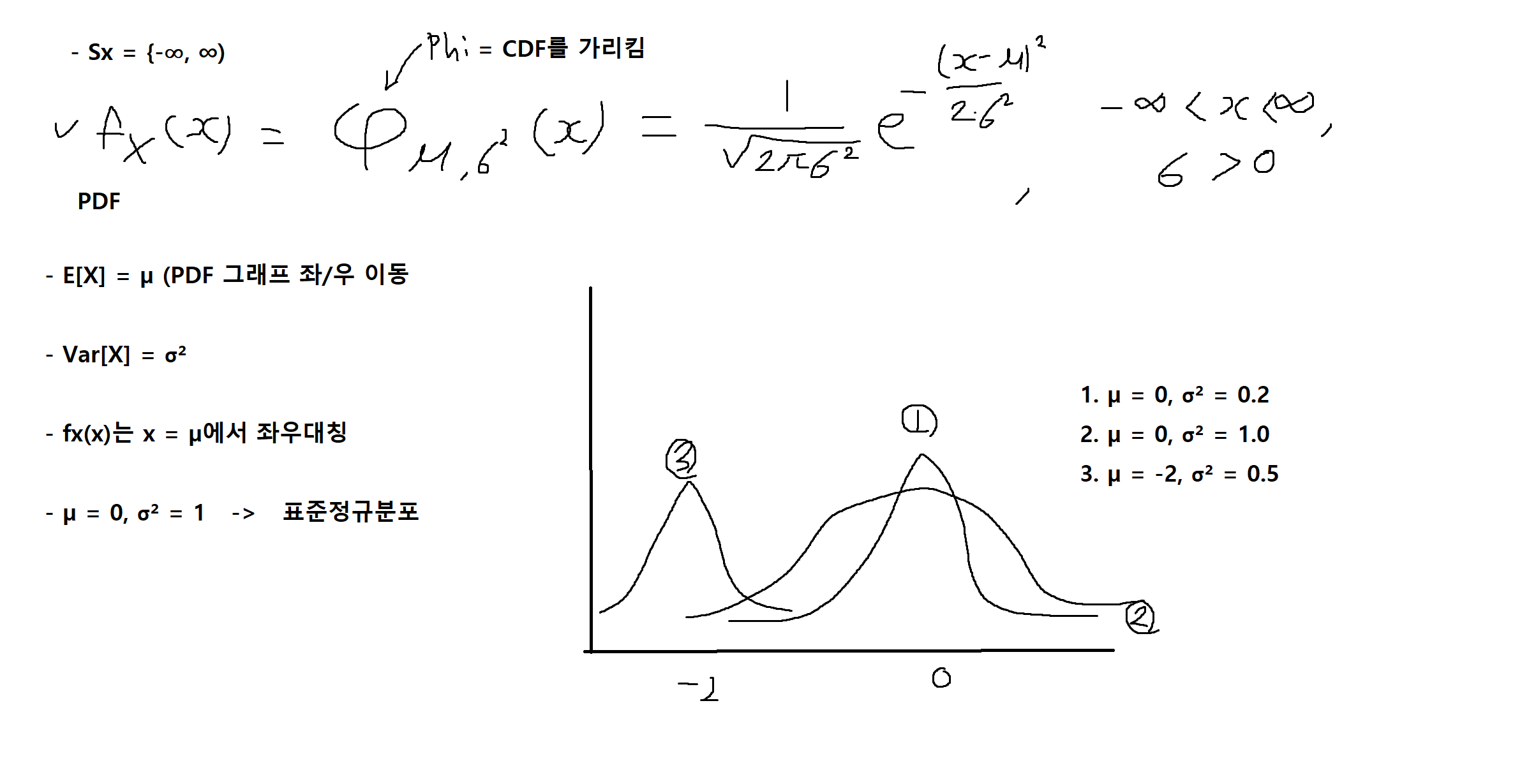
가우스 확률변수 또는 정규분포 (normal distribution) (가우스 분포)

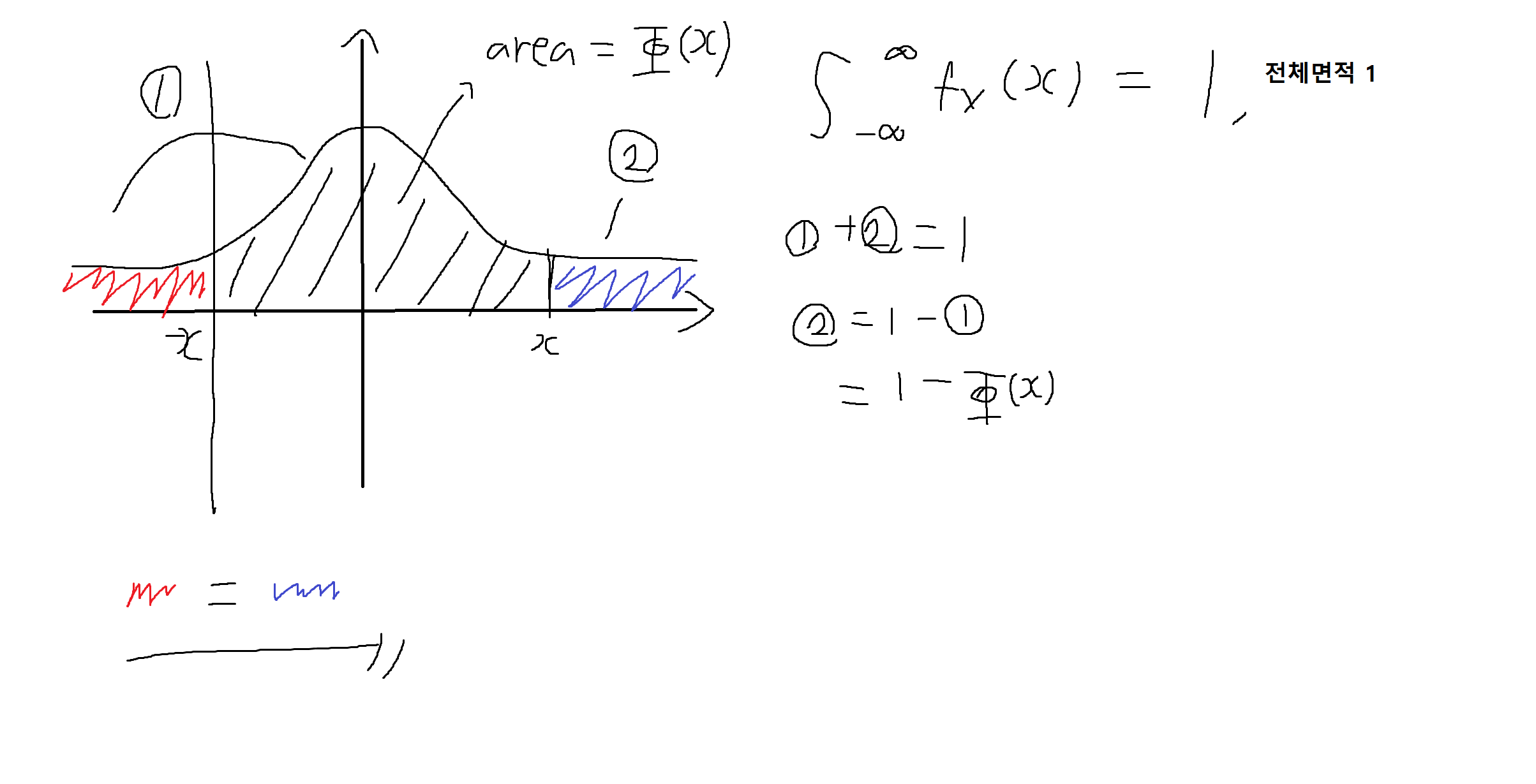
예제 4-19: 평균이 0이고 분산이 1인 표준정규분포를 따르는 확률변수 Z의 누적분포함수(CDF) Φ(z)는 구간 0 <= z <= 2.2에서 다음과 같이 근사할수 있다.
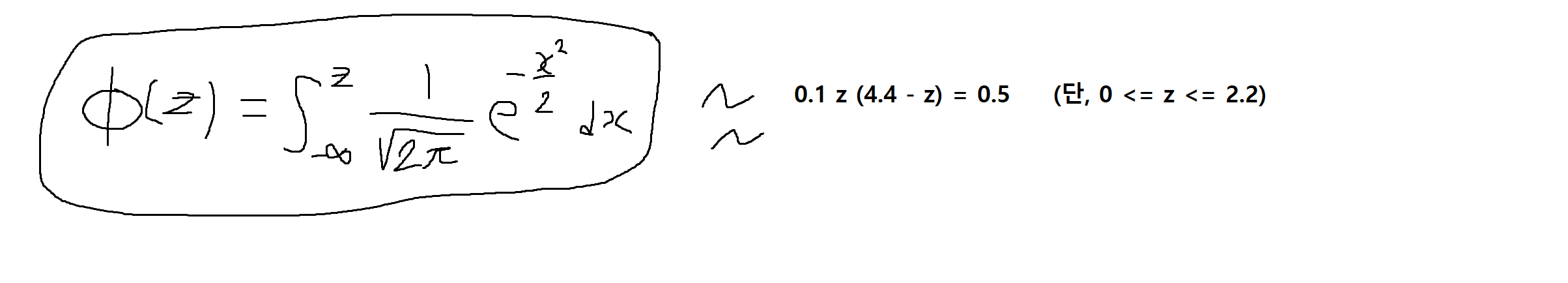
확률변수 X는 평균이 5이고 분산이 4인 가우스 확률변수일 때, 위의 수식 (근사)를 이용해서 다음의 확률값을 구해라.
(1) P[X <= 9]
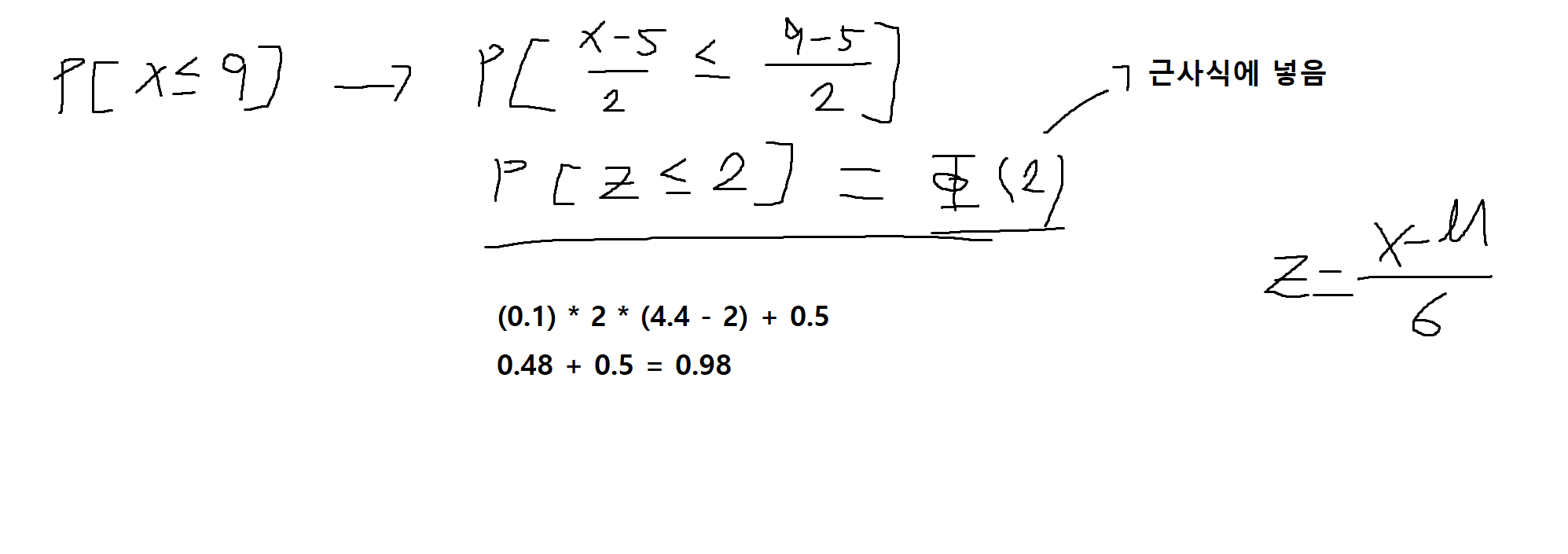
(2) P[X <= 3]