자료구조 중 선형 자료구조의 가장 기본적인 형태라고 할 수 있는 선형 배열(Linear Array)에 대해서 알아보자.

선형 자료 구조란?

선형 배열을 알아보기 전에 선형 자료 구조(linear data stucture)는 무엇일까?

연속적으로 데이터가 나열되는 자료구조로써, 하나의 데이터 뒤에 다른 하나의 데이터가 연결되는 형태이다. 자료들 앞뒤 관계는 1:1 관계이다.

선형 자료구조로는 배열, 연결 리스트, 스택, 큐 등이 있다. 이번 글에서는 '배열(Array)'에 대해서만 생각해본다.

배열(Array)이란?

배열은 정해진 크기만큼 데이터가 일렬로 저장되는 정적(static) 자료구조다.

각 데이터를 배열의 요소(element)라고 하며 데이터를 가리키는 번호를 인덱스(index)라고 한다. 즉, 배열은 번호(index)가 붙혀진 이어져 있는 칸(메모리가 연속적)에 원소(element)들을 채워넣는 방식이다. index를 가지고 있기 때문에 접근과 탐색에 용이하게 사용할 수 있다.

python에서는 list를 사용하여 배열을 나타낸다.

python list vs array

사실 나는 python을 주언어로 사용하기 때문에 배열에 대해서 다른 언어와는 약간 다른 개념을 가지고 있다.

python에서 사용하는 list는 다른 언어와 개념이 다르며 배열과 비슷한 의미로 사용한다.

• 공통점
  • index를 가지고 있다.
• 차이점
  • list는 메모리가 연속적이지 않을 수 있다.
  • list는 동적이며, 데이터 타입, 길이가 서로 달라도 된다.

배열의 연산

1. 원소 덧붙히기

list를 사용한 연산에서 원소를 뒤에 붙히는 것은 append() 메소드를 사용한다.

a = [1, 2, 3]
a.append(4)  # [1, 2, 3, 4]

2. 끝에서 꺼내기

끝에서 꺼내기 위해서 pop() 메소드를 사용한다.
pop() 메소드는 끝에 있는 원소를 제거하는 동시에 끝의 값을 반환한다. 특정한 위치의 값을 빼고 싶으면 pop(index) index값을 넣으면 해당하는 위치의 원소를 제거하고 반환한다.

a = [1, 2, 3]
b = a.pop()

print(a)  # [1, 2]
print(b)  # 3

3. 원소 삽입하기

원하는 위치에 원소를 삽입하기 위해서는 insert(idx, value) 메소드를 사용한다.

a = [1, 2, 3]
a.insert(1, 4)

print(a)   # [1, 4, 2, 3]

4. 원소 삭제하기

삭제는 del(arr[idx]) 함수를 사용한다.

a = [1, 2, 3]
del(a[1])

print(a)    # [1, 3]

5. 원소 탐색하기

원소가 어느 위치에 있는지 알고 싶을 때 index(value) 메소드를 사용한다.

a = ['a', 'b', 'c']

print(a.index('c'))  # '2
print(a.index('d'))  # 없는 원소는 에러가 난다.

배열의 연산에 따른 시간 복잡도

연산	시간 복잡도
덧붙히기	O(1)
끝에서 꺼내기	O(1)
원소 삽입	O(n)
원소 삭제	O(n)
원소 탐색	O(n)

배열의 정렬

정렬이란, 복수의 원소로 주어진 데이터를 정해진 기준에 따라 새로 늘어놓는 작업이다. 정렬에는 여러가지 알고리즘이 있지만 python에는 배열을 정렬하는 메소드와 함수가 있기 때문에 따로 구현하지 않아도 된다.

• 기본적으로 사전 순서(오름차순)를 따르며, 대문자가 소문자보다 우선시 된다.
• 정렬의 순서를 반대로 하고 싶다면 reverse=True 인자를 추가한다.
• 사전 순서가 아닌 독자적인 규칙을 만들고 싶다면 key라는 인자에 익명 함수(lambda)를 이용하여 지정한다.

1. sorted() 함수
   python 내장 함수이다. 정렬된 새로운 list를 만든다.

   L = ['hij', 'ab', 'efgh']
   sort_L = sorted(L)
   
   print(sort_L)    # ['ab', 'efgh', 'hij']
   
   # 역순 정렬
   sort_L2 = sorted(L, reverse=True)
   print(sort_L2)   # ['hij', 'efgh', 'ab']
   
   # key 사용(예: 문자열 길이 순)
   sort_L3 = sorted(L, key= lambda x: len(x))
   print(sort_L3)   # ['ab', 'hij', 'efgh']

2. sort() 메소드
   list의 내장 메소드이며, 해당 리스트를 정렬한다.

   L = ['hij', 'ab', 'efgh']
   L.sort()
   
   print(L)   # ['ab', 'efgh', 'hij']
   
   # 역순 정렬
   L.sort(reverse=True)   
   
   print(L)   # ['hij', 'efgh', 'ab']
   
   # key 사용 (예: 문자열 길이 순)
   L.sort(key= lambda x: len(x))
   
   print(L)   # ['ab', 'hij', 'efgh']
   
   # key도 역순 정렬 가능
   L.sort(key= lambda x: len(x), reverse=True)
   print(L)   # ['efgh', 'hij', 'ab']

   
   

다중 조건 정렬

다중 조건이라면 어떻게 해야할까?
예를 들어 문자열의 길이로 정렬하고, 같은 길이일 경우 첫번째 문자열을 사전식 배열하고 싶다면?
방법은 똑같이 key 인자를 사용하는데 익명함수의 return값에 튜플로 차례대로 기입해주면 된다.

L = ['ebv', 'hzjk', 'ec', 'kamk']
L.sort(key= lambda x: (len(x), x[1])) 
print(L)  # ['ec', 'ebv', 'kamk', 'hzjk']

배열의 탐색

탐색이란, 복수의 원소로 이루어진 데이터에서 특정 원소를 찾아내는 작업이다. 위에서 확인했던 index() 메소드와 같은 일을 하는 알고리즘에 대해서 생각해보자.
탐색 알고리즘에는 다양한 방식이 있지만, 여기서는 2가지 방식만 확인해고자 한다.

1. 선형 탐색 (Linear Search, 순차 탐색)

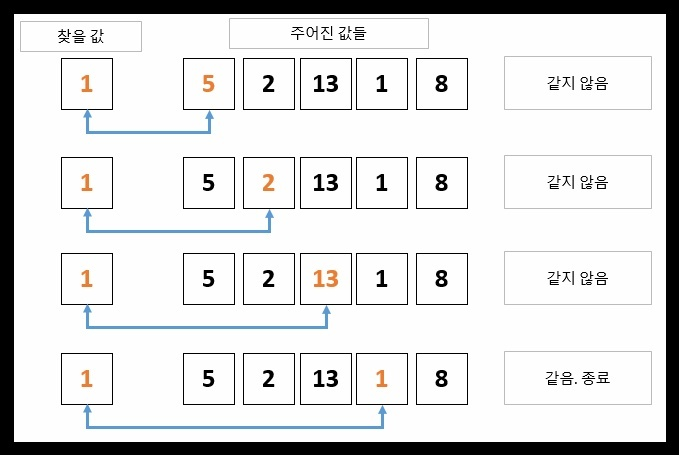
• 순차적으로 모든 요소들을 탐색하여 원하는 값을 찾아낸다.
• 배열의 길이에 비례하는 시간이 걸린다. => $O(n)$
• 최악의 경우 즉, 찾고자 하는 원소가 마지막 원소에 있다면 배열에 있는 모든 원소를 다 검사해야 한다.
  

def linear_search(L, x):
	i = 0
	# 주어진 배열 L을 넘어서지 않고, x와 같아지기 전까지 반복한다.
	while i < len(L) and l[i] !=x :
    	i += 1
	# i가 L의 길이보다 작다면 return
	if i < len(L):
		return i
	# i가 L의 길이보다 크다면 찾는 원소가 없는 것
    else:
       return -1

2. 이진 탐색 (Binary Search)

• 이진 탐색은 선형 탐색과는 다르게 탐색하고자 하는 배열이 이미 정렬되어 있는 경우에만 적용 가능

• 정렬되어 있다는 성질을 이용하여 이진 탐색은 배열의 가운데 수와 찾고자하는 원소의 크기를 비교하여 왼쪽 혹은 오른쪽을 버려가며 탐색한다.
  

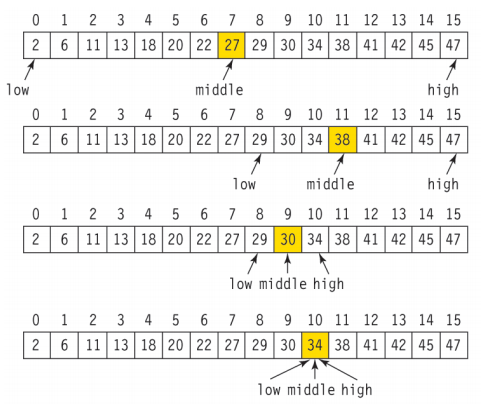
• 위에 그림처럼 맨 처음에는 low(코드에서는 lower), 맨 끝에는 high(코드에서는 upper), 가운데에 middle을 두고 시작한다.

• middle의 값이 찾고자하는 x보다 크면 high의 위치를 조정하고, x보다 작으면 low의 위치를 조정하면서 x의 위치를 찾는다.

• 이처럼 한번 비교가 일어날 때마다 리스트가 반씩 줄어든다 => $O(\log a)$

def binary_search(L, x):
	# lower, upper 값 세팅
	lower = 0
	upper = len(L)-1
    
    # upper가 lower보다 작아지는 졌다면 해당 숫자가 없는 것이다.
    while lower <= upper:
    	# middle은 lower와 upper의 중간지점
    	middle = (upper+lower) // 2
        # middle과 x가 같다면 해당 인덱스 반환
		if L[middle] == x:
        	return middle
        # x가 middle보다 크다면 lower을 조정
		elif L[middle] < x:
        	lower = middle + 1
        # 반대로 작다면 upper을 조정한다.
		else:
        	upper = middle - 1
	return -1

항상 이진 탐색?

이 두가지를 비교했을 때 이진 탐색의 시간 복잡도가 더 효율적이라서 항상 이진 탐색을 사용해야할까?

이진 탐색은 정렬이 되어있는 경우에만 사용할 수 있기 때문에, 정렬이 되어있지 않은 배열이라면 정렬하고 또한 원래의 위치를 기억하는 변수가 또 있어야 한다.

정렬이 되어있지 않은 배열이라면 선형 탐색을 사용하는 것이 더욱 효율적이다.

정렬이 되어 있으면 이진 탐색, 안 되어 있으면 선형 탐색

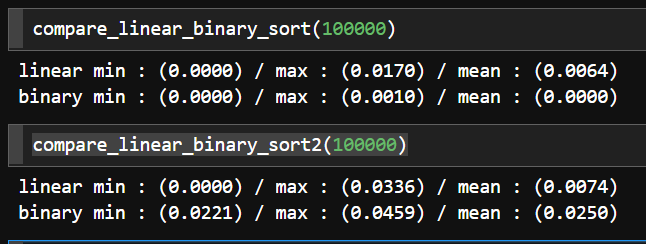
위의 함수는 정렬이 되어있는 경우, 아래의 함수는 정렬이 되어있지 않은 경우에 대한 시간 비교이다. 랜덤으로 10만의 크기를 갖는 리스트를 랜덤의 위치를 찾을 때 시간을 비교해 봤다. (이 크기 보다 작을 때는 0초였다...)
정렬이 되어있을 때는 이진탐색이 압도적으로 빠르지만 정렬이 되어있지 않을 때는 정렬하는 시간까지 합치기 때문에 선형탐색이 더 빠른 것을 확인할 수 있었다.