python에는 기본적으로 제공하는 자료형이 있다.
int, str, list, dictionary 등 우리가 사용할 수 있는 다양한 자료형이 있지만 다뤄야하는 데이터가 많아지고 문제가 복잡해지면 내장된 자료형만으로는 효율적인 코드를 작성할 수 없다. 이때 필요한 것이 바로 자료 구조(data stucture)이다.
자료 구조가 뭔데?
자료 구조는 이름에서 뜻하는 것처럼 데이터를 구조적으로 모은 것을 말한다. 각 원소들이 논리적으로 정의된 규칙에 의해 나열되며 자료에 대한 처리를 효율적으로 하기 위해 데이터에 적용할 수 있는 연산을 가지고 있는 구조이다.
연산에 사용되는 메모리 자원은 매우 한정적인데 처리해야 할 데이터가 무수히 많아서 메모리 공간을 효율적으로 사용해야 할 때, 빠른 시간안에 처리해야 하는데 데이터가 무수히 많아서 실행 시간을 효율적으로 사용해야 할 때 자료 구조를 사용한다.
위의 내용을 읽다보면, "이런건 알고리즘 문제 아니야?" 라고 생각할 수 있다. 알고리즘과 자료 구조는 떨어질 수 없는 관계이다. 알고리즘이란, 주어진 문제의 해결을 위한 자료 구조와 연산 방법에 대한 선택이라고 할 수 있다. 해결하고자 하는 문제에 따라 최적의 해법은 모두 다르기 때문에 다양한 자료 구조의 형태와 장단점을 알고 있어야 한다.
내가 어떤 자료 구조를 택해서 어떤 특정한 문제를 풀 것인가?
풀어야 하는 문제를 파악하고 내가 이용하고자 하는 자료 구조가 어떤 성질을 가져야 하는지에 대해 파악하는 것이 알고리즘 문제를 풀 때 해야하는 첫 번째 생각이다.
자료 구조 종류
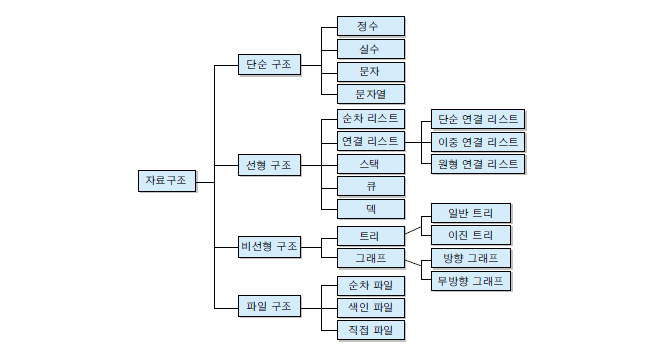
자료 구조의 아래의 그림처럼 여러가지 종류가 있다.
하나하나 차근차근 정리를 해보자.
(하나하나 추가할 예정!)
선형 배열(Linear Arrays)
단순하게 말하자면 원소들을 순서대로 늘어놓은 것이다.
python에서는 list를 사용하고, 다른 언어들과는 다르게 데이터 타입과 길이를 통일하지 않아도 된다.
배열은 정적(static) 자료구조로써 정해진 크기만큼 데이터가 일렬로 저장이 된다. 해당 크기만큼 연속된 메모리 주소를 할당받게 되고 각 요소에 대한 인덱스를 가지고 있다.
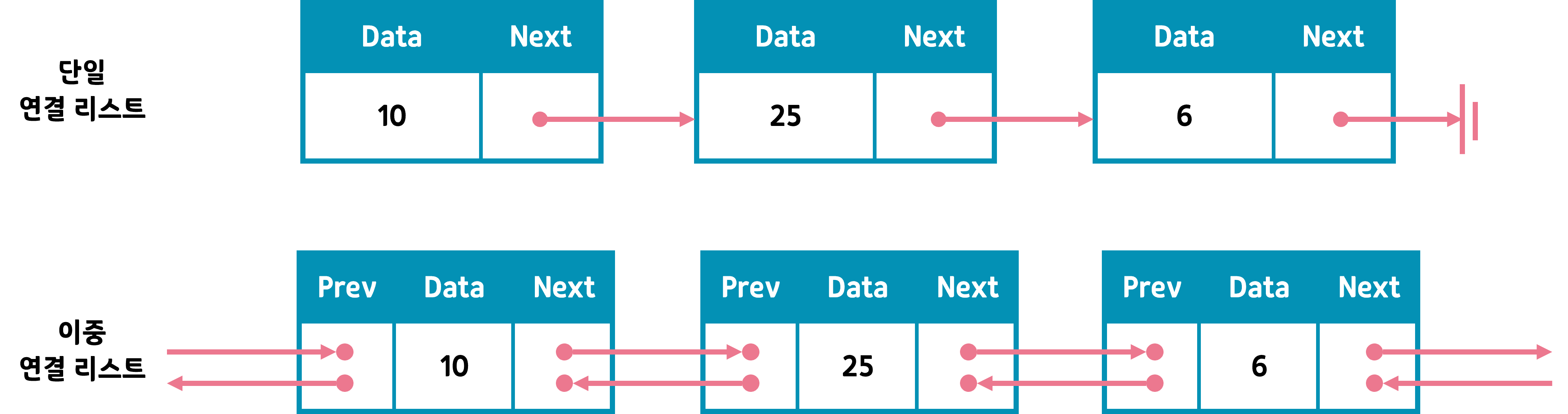
연결 리스트(Linked List)
연결 리스트는 각 원소들을 줄줄이 엮어서 관리한다.
대표적인 선형 자료구조 중 하나로, 배열과 달리 크기가 정해져 있지 않은 동적(dynamic) 자료구조이다. 여러 개의 노드(Node)로 구성되어 있고 각 노드는 데이터(data)와 앞/뒤 노드를 연결해주는 링크(Link)을 가지고 있다. 이런 Node를 이용하여 데이터의 삽입/삭제를 보다 빠르게 할 수 있다는 장점을 가지고 있다.
연결 리스트는 크게 3가지 종류가 있다.
1) 단방향 연결 리스트(Singly Linked List)
2) 양방향 연결 리스트(Doubly Linked List)
3) 원형 연결 리스트(Circular Linked List)
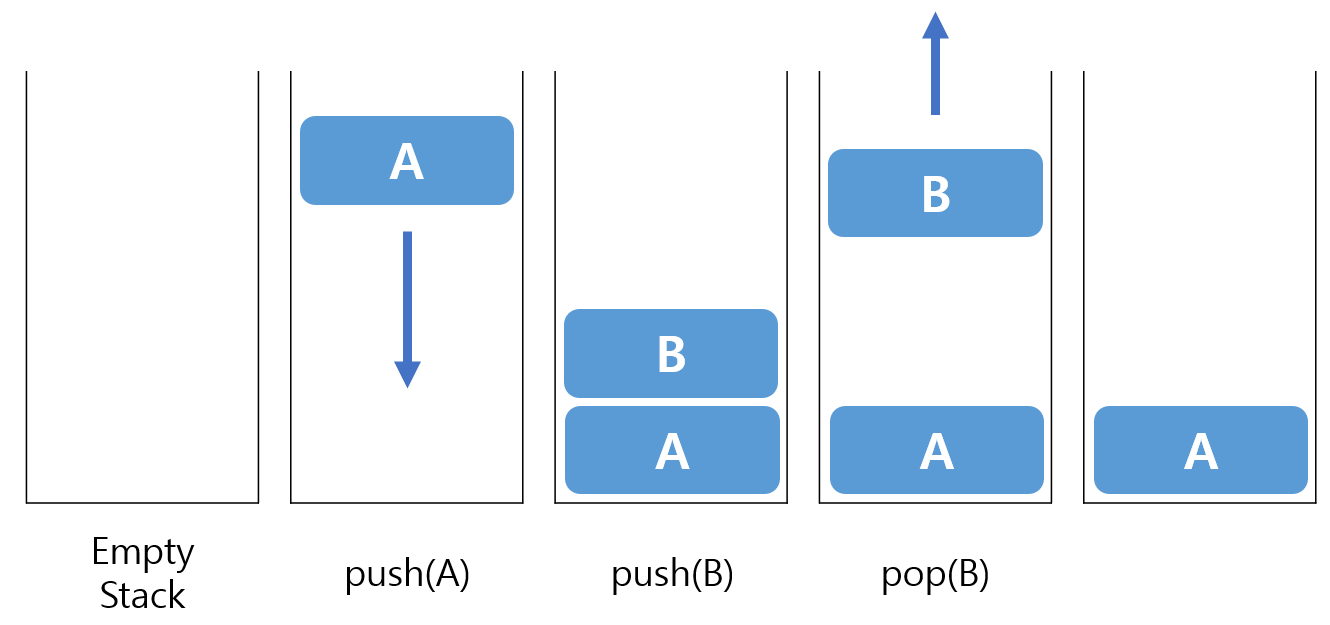
스택(Stack)
스택은 말그대로 데이터를 쌓아서 보관하는 구조이다. 단, 넣을 떄에는 한 쪽 끝에서 밀어 넣어야 하고(push), 꺼낼 때에는 같은 쪽에서 뽑아 꺼내야 한다(pop). 간단히 말해서 원통에 뚜껑을 열고 과자를 차례로 넣었다가 위에서 빼내가는 형태이다. 이것을 LIFO(Last In First Out, 후입선출) 형태라고 부른다.
이런 성질을 이용하여 중위 표기법을 후위 표기법으로 전환하여 계산할 수 있다.
큐(Queue)
큐는 데이터가 순차적으로 들어왔다가 나가는 형태로, 넣을 때에는 한쪽 끝에서 밀어넣고(enqueue) 꺼낼 때는 반대 쪽에서 뽑아 꺼내야(dequeue)한다. 쉽게 생각하면 위 아래가 모두 뚫린 원통에 과자를 집어넣고 반대로 꺼내는 것이다. 이것은 FIFO(First in, First Out, 선입선출) 구조라고 부른다.
큐는 React의 렌더링 실행 순서에 사용되며, OS의 구조에서 많이 보인다. 특히, 비동기적으로 일어나는 작업에 사용한다.
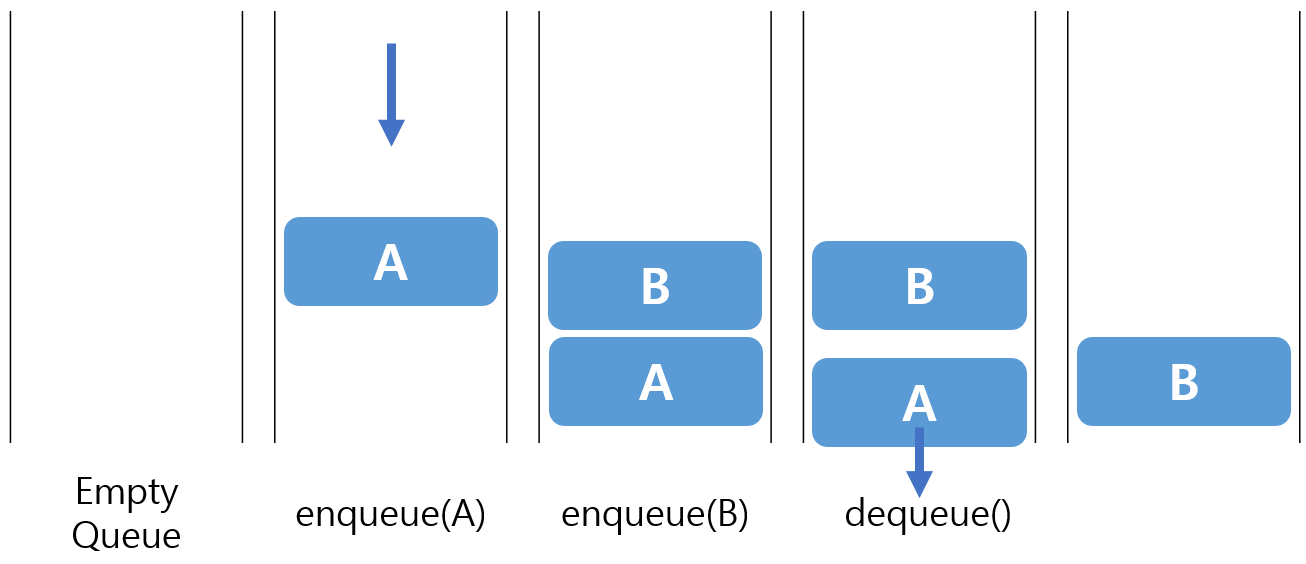
큐 또한 여러 종류를 가지고 있다.
1. 선형 큐 (Queue)
2. 환형 큐 (Circular Queue)
3. 우선순위 큐 (Priority Queue)
트리(Tree)
트리는 대표적인 2차원 구조의 자료 구조이다. 트리는 그래프의 한 종류인데, 계층적인 관계를 표현할 때 사용한다.
정점(Node)과 간선(edge)를 이용하여 데이터의 배치 형태를 추상화한다. 트리구조는 HTML 구조의 뼈대이기 때문에 잘 알아둘 필요가 있다.
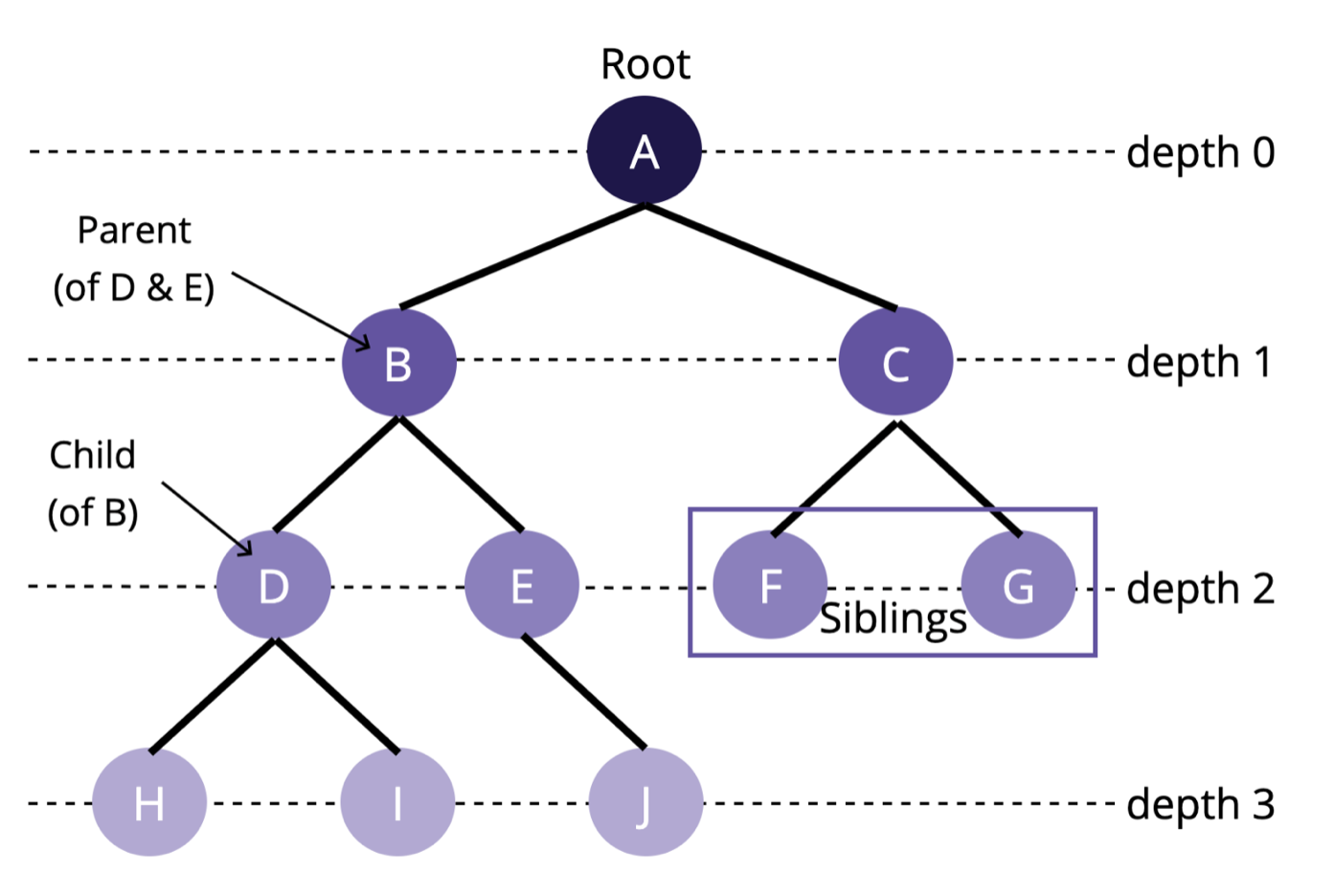
트리 중 자식 노드가 최대 2개인 트리를 이진 트리(Binary Tree)라고 부른다. 이진 트리는 2가지 종류가 있다.
1. 완전 이진 트리(Complete Binary Tree)
2. 포화 이진 트리(Perfect Binary Tree)