원본은 여기!
접근
아직 문제마다 어떤 알고리즘을 써야 할지 잘 모르겠어서 DP면 DP, 그래프면 그래프, 이런 식으로 주제를 정해놓고 잘 알려진 문제들 먼저 쭉 풀어보고 있다.
간단한 DP 문제를 풀다가 여기서 막혔는데, 처음엔 숫자가 100자리라길래 리스트에 100자리, 그러니까 0부터 999...999까지의 답을 기록해놓고 bottom-up 해야 하는건가? 싶어서 살짝 당황했었다.
그런데 아무리 생각해도 그건 좀 아닌 것 같아서 자릿수별 답을 저장해 놓고 bottom-up 하는 접근 방법을 생각해봤었다. 그럼 DP 리스트의 길이가 100이면 될거고,, 하는 식으로 접근하는데 이번에도 묘한 패턴만 보일 뿐 딱히 진전이 없는 것 같았다. (사실 여기서 어느정도 아이디어는 얻어 놓은 것 같다.)
0으로 시작하는 계단 수는 취급하지 않는다고 하니까, bottom에 있는 값은 한 자리의 계단 수 개수인 9개(1~9)로 생각하고 풀이를 시작했다.
mem = [0 * 101] # 1자리 계단수의 개수를 mem[1]로 접근하려고 이렇게 씀!
mem[1] = 9다음으로 2자리의 계단수의 개수를 구하기 위해 하나씩 케이스를 써보면,,
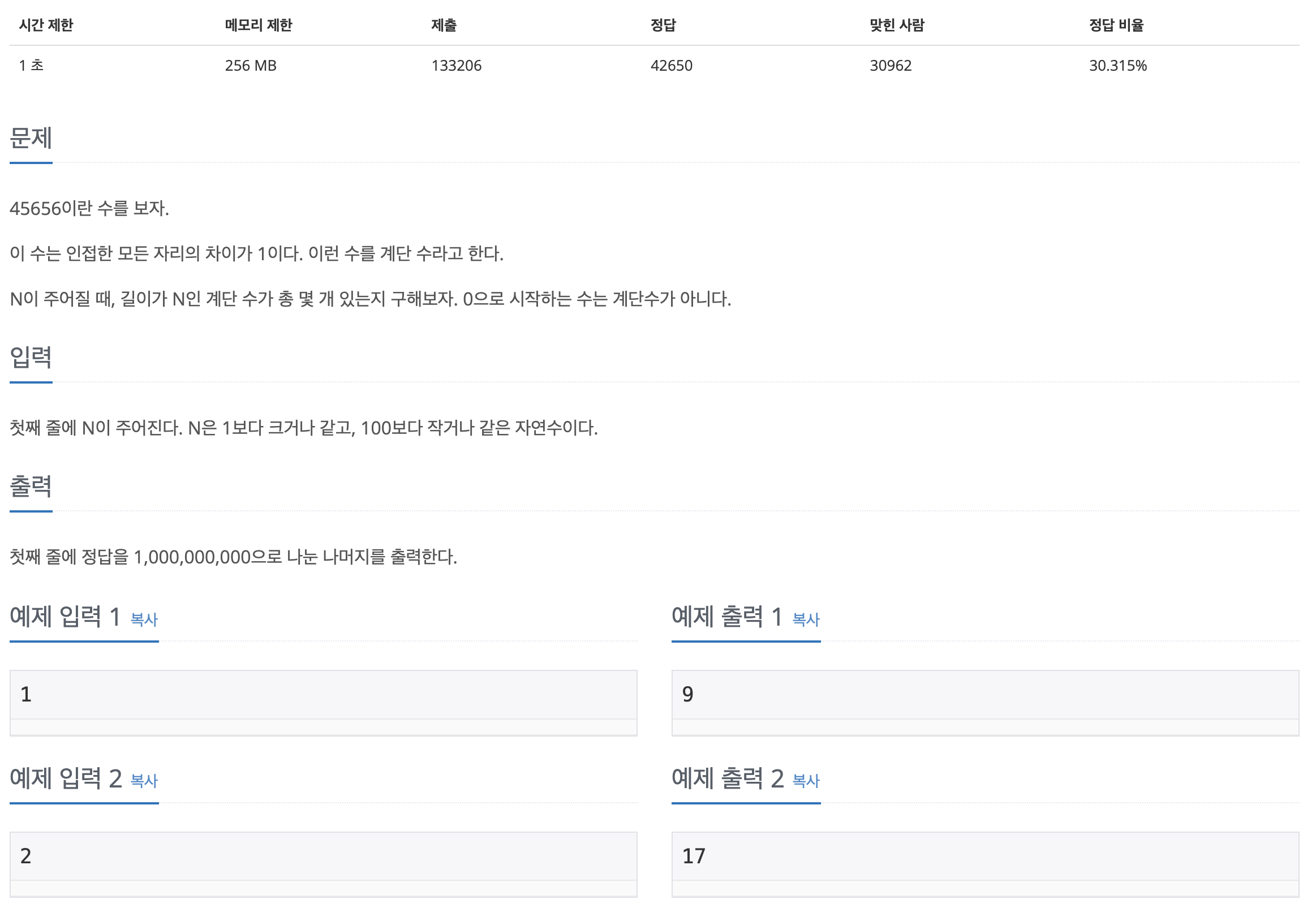
2자리이면서 0으로 끝나는 계단 수는 10으로 한 개 밖에 없으므로, mem[2]에 1을 더한다. (mem[2] = 1)
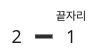
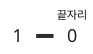
2자리이면서 1로 끝나는 계단 수도 21으로 한 개 밖에 없으므로, mem[2]에 1을 더한다. (mem[2] = 2)
2자리이면서 3으로 끝나는 계단수는 13과 32로 두 개가 있고, 이 패턴이 2자리이면서 8로 끝나는 78과 98까지 이어진다. 그러므로 2~8로 끝나는 계단 수의 개수는 2*7=14개, 즉 mem[2]에 14를 더해 mem[2] = 2 + 14 = 16이 된다.

2자리 계단 수 중 마지막 9로 끝나는 계단 수는 89밖에 없으므로, mem[2]에 1을 더해 mem[2] = 16 + 1 = 17이 된다. 와!
그런데,,
아마 이렇게 구하다보면 뭐라고 해야 하나, dp 리스트에 'n자리' 까지의 정보만 남아 있지, '맨 마지막 자릿수'에 대한 정보가 빠져 있기 때문에 저런 방법으로 구하는게 가능한지는 둘째치고 계산이 좀 복잡했다.
뭔가 패턴을 잘못 찾은건가 한참 해메고 있다가 어제 친구랑 얘기하던 도중 이 문제 얘기가 나와서 예전 풀이를 잠깐 보여줬는데, 2차원 배열로 dp 테이블을 만들어서 문제를 해결하고 있었다. 오 뭔가,, 보일 것도 같은데,,?
그래서!
dp 테이블에 'n자리' 뿐만 아니라 '맨 마지막 자릿수'에 대한 의미도 남겨 놓기 위해, mem[k][m]에 k자리의 m으로 끝나는 계단 수의 갯수 저장 하도록 생각을 바꿔 풀어봤다.
그럼 한자리의 계단수 갯수는 아래와 같이 초기화할 수 있을 것이다.
# mem[k][m] = k자리이면서 m으로 끝나는 계단수의 개수
mem = [[0] * 10 for _ in range(101)]
# 0은 계단수가 아니므로 (헷갈릴까봐 명시적으로 다시 써줌 ㅎ)
mem[1][0] = 0
# 1~9는 그 자체로 계단수이므로 mem[1][i]는 1 (i>1)
for i in range(1, 10):
mem[1][i] = 1위의 살짝 부족했던 패턴을 반복해서 쓰다보면, 아래와 같은 모양의 테이블로 떨어진다.
| 자리수\끝자리수 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
저 저,, 볼드 처리된 칸만 유독 다른 값을 가지는 이유를 생각해보면, 2자리 기준으로 0으로 끝나는 수는 앞자리가 1인 10 밖에 없고, 1로 끝나는 수는 계단수가 0으로 시작할 수 없기 때문에 21 밖에 없으며, 9로 끝나는 수는 앞자리가 8인 89 밖에 없기 떄문이다.
이외의 수들, 그러니까 끝자리가 2부터 8까지에 해당되는 수들은 각각 끝자리보다 1보다 크거나 작은 값들을 그 앞자리 수로 가지기 때문에 2개씩 갯수가 나오는 것이다.
좀 번거롭긴 하겠지만, 3자리 계단수까지 한 번 구해볼까?
| 자리수\끝자리수 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 |
| 3 | 1 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | 3 | 2 |
슬슬 패턴이 보인다. 예상컨데 자기 대각선 위의 왼쪽, 오른쪽 칸의 값을 더한 값을 자기 칸에 쓰되, 맨 왼쪽(0)과 오른쪽(9)는 각각 자기 대각선 오른쪽 위, 자기 대각선 왼쪽 위를 쓰면 된다.
이게 왜 이렇게 나타나는지는 아까와 같은 그림으로 설명할 수 있다.
아하 DP!
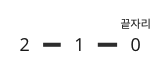
3자리이면서 끝자리가 0인 계단수는 210 밖에 없다. 맨 끝자리인 0과 맞닿아 있을 수 있는 수는 1밖에 없고, 1과 맞닿아 있을 수 있는 자릿수는 2밖에 없기 떄문이다.
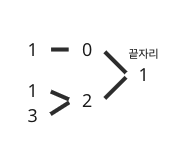
3자리이면서 끝자리가 1인 계단수는 101, 121, 321로 총 3개가 있다. 그런데 이거, 낯익은 부분이 보이는데,,

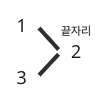
바로 이 부분이다. 아까 2자리의 계단수 갯수를 기록하면서 봤던 그림인데, 끝자리 수가 1인 수의 그 앞자리 수는 0과 2가 올 수 있는데, 그 앞자리 수가 계단수를 유지할 수 있는 경우의 수를 각각 mem[2][0], mem[2][2]에 기록할 수 있으므로 mem[3][1], 그러니까 3자리이면서 끝자리가 1인 계단수의 개수는 mem[2][0] + mem[2][2]가 되는 것이다!
아니 날아가버렸네 (...)
방금 마무리 코드까지 다 썼는데 뒤로가기를 잘못 눌러서 다 날아갔다. 컨디션도 나쁜데 쓰으,,,
요점은, n자리면서 k로 끝나는 계단수에서 맨 끝자리를 제외한 그 앞자리 수들 역시 계단수의 조건을 만족하므로, 그 앞자리의 값(들)을 더해 bottom-up 해주면 풀리는 문제다.
from sys import stdin
input = stdin.readline
def solution(n: int) -> int:
mem = [[0] * 10 for _ in range(101)]
mem[1][0] = 0
for i in range(1, 10):
mem[1][i] = 1
for digit in range(2, n + 1):
mem[digit][0] = mem[digit - 1][1]
for i in range(1, 9):
mem[digit][i] = mem[digit - 1][i - 1] + mem[digit - 1][i + 1]
mem[digit][9] = mem[digit - 1][8]
return sum(mem[n]) % 1000000000
if __name__ == "__main__":
n = int(input())
print(solution(n))컨디션 조절을 잘 하자.
어제 오늘 몸이 좀 으실으실한게 일도 잘 안잡히고 해서 잠깐 머리 풀겸 문제 하나 풀어봤는데, 어째 영 더 안좋은 것 같다(...)
이 글 보고 있는 누군가는 부디 건강 잘 챙기길 바랍니다. 안녕,, 파들파들,,

