LIS : Longest Increasing Subsequence

급식·2023년 11월 14일

알고리즘

목록 보기

6/12

2631 줄세우기라는 문제를 풀다가 핵심 아이디어로 LIS를 구하는 알고리즘이 포함 되어 있다길래, 공부한 내용을 한 번 정리해보려고 한다.

LIS는 Longest Increasing Subsequence, 즉 가장 긴 증가하는 부분 수열이다. 꽤 유명한 문제인지 같은 제목 같은 내용으로 S2짜리 1번부터 P5짜리 5번(!!)까지 있다. 오늘은 2번까지만 풀어볼거긴 한데, 내공을 쌓으면서 혹시 뒷쪽 문제도 풀리면 정리해놓겠다. 알고리즘 풀면서 느끼는건데 간혹 이렇게 엄청 간단해보이는데 풀기 어려운 문제가 왕왕 있는 것 같다. 정진,, 또 정진,,

가장 쉬운 접근 : DP

1번 난이도로, 11053번 문제에 해당된다.

LIS의 정의가 짧게 설명되어 있는데, 저게 전부다. 'Substring' 이 아니라 'Subsequence' 이기 때문에 요소들이 붙어있을 필요가 없고, 그저 요소들이 증가하는 순서대로 배열되어 있기만 하면 된다.

가장 간단하고 쉬운 방법은 순서만 지켜지도록 k개(n개~1개)의 요소를 뽑아 subsequence를 만들어 주고, 이 부분 수열이 증가하는지 확인한 다음 맞을 경우 그 값을 반환해주면 된다.

,,물론 이 방법은 가장 간단한만큼 효율이 나쁘다. 당장 순열을 구하는 알고리즘의 시간 복잡도가 O(N!)이기 때문이다.

이 방법의 비효율성은 이전의 정보, 그러니까 이전에 LIS를 발견했다는 사실과 정보를 다시 재활용하지 않기 때문에 발생한다. 그럼 뭐다? DP를 써보면 되겠다!

코드

def solution(arr: List[int]):
    dp = [1 for _ in range(len(arr))]

    for i in range(1, len(arr)):
        base_num = arr[i]
        for j in range(i):
            if arr[j] < arr[i]:
                dp[i] = max(dp[i], dp[j] + 1)

    return max(dp)

코드를 먼저 보니까 좀 어려울 수 있는데, 그림으로 생각해보면 쉽다.

해설

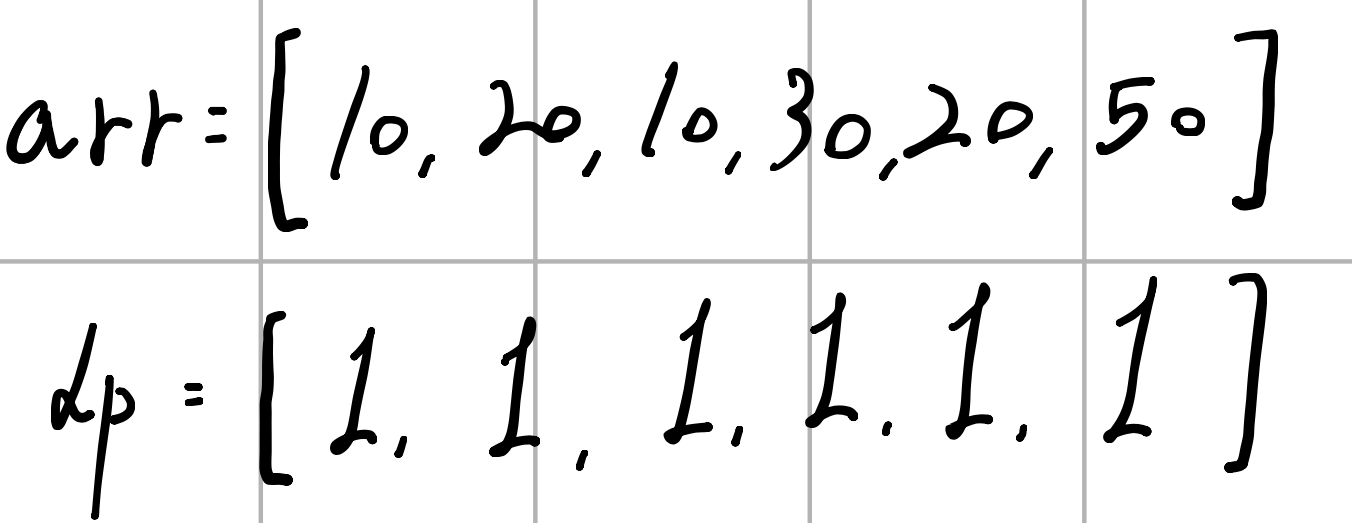
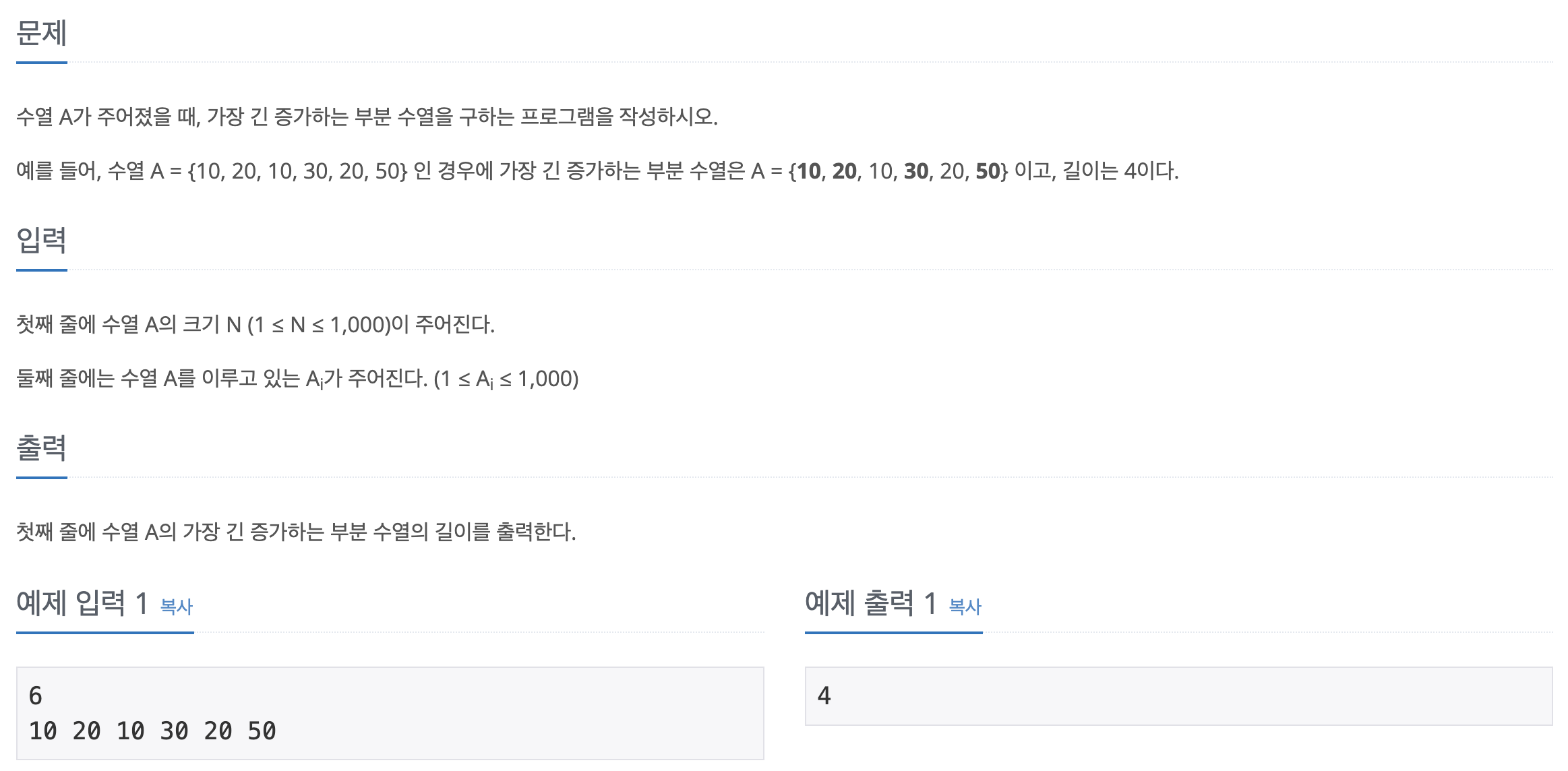
처음엔 이렇게 시작하자. 여기서 dp[x]는 arr[x-1]을 반드시 끝 요소로 하고, arr[0:x+1] 구간에 속해 있는 LIS의 최대 길이이다. 예를 들어 dp[2]은 {.. , 10} 형태인 부분 수열의 길이여야 하는데, 눈으로 훑어 보면 알겠지만 그런 조건을 만족하는 LIS는 없으므로 dp[2]는 1이 될 것이다. {10, 20}은 조건을 만족하지 않는다!!!!

그리고 base_num이라는걸 쓰고 있는데, 이건 보다시피 앞에서부터 다른 수들과 비교할 기준 수이다. 그 다음 j에 대한 for문을 살펴보면 [0, i) 범위에 대해 반복하도록 되어 있는데, i=0이면 반복이 없으니까 i=1, i=2, i=3까지 손으로 실행 흐름을 옮겨보자.

타란,, 위에서 볼드체로 강조한 이유가 있다. 여기서 재활용한 정보는 바로 이전 구간까지의 최대 LIS 길이이다. 단 arr[j] < base_num에서 알 수 있듯 반드시 LIS의 맨 끝 요소가 arr[j]여야 한다. 그래야 base_num을 해당 LIS의 끝에 붙일 수 있는지 없는지를 해당 조건문 하나만 확인해서 결정할 수 있기 때문이다.

이를테면 i=3일 때,j=0, arr[0]=10이고, (arr[0]=10) < (arr[3]=30)이다. 이는 즉 {10}이라는 LIS의 맨 마지막 값이 10임을 알고 있으므로, 앞의 모든 수를 다 확인할 필요 없이 해당 LIS의 가장 큰 값이 10임을 알 수 있다. 이때 조건문을 통해 30이 해당 LIS의 끝 요소가 될 수 있는지 확인해본 결과 가능하므로, 기존 LIS의 길이에 1만큼 더해진 값(dp[0]+1)으로 dp[3]이 갱신된 것이다.

또 i=3, j=1일 때 arr[1]=20이므로, (arr[1]=20) < (arr[3]=30)이다. 이는 마찬가지로 20을 맨 끝으로 가지는 LIS의 가장 긴 길이가 2였음을 의미하므로({10, 20}) 20과 30만 비교해서 이 LIS에 30을 추가할 수 있는지 확인할 수 있다.

물론 추가할 수 있으므로 길이를 구해주고(dp[2]+1=3), 이 값이 기존의 LIS인 {10, 30}보다 길기 때문에 이 값으로 갱신해주면 된다.

처음엔 생각 없이 반복이 모두 끝난 후 dp[len(arr)-1]를 결과로 반환했는데, 이러면 안된다. arr[-1]을 가장 끝 수로 하는 LIS의 길이가 가장 길다고 확신하여 결과로 반환한 셈인데, 이런 논리면 {10, 20, 30, 40, 50, 10}의 결과가 5가 아닌 1이 나오겠지?

분석

위에서 LIS의 최대 길이를 구하기 위해 사용한 계산은 얼마나 많을까?

for문이 2개인 시점에서 알 수 있듯 일단 O(N^2)이고, Big-O notation이므로 묻히겠지만 맨 마지막의 max 함수 호출을 통해 N번의 비교가 추가적으로 필요할 것이다.

이전의 무식한 O(N!) 해결법보단 많이 나아졌으므로, 목표로 한 Silver 2 난이도는 무사히 통과할 수 있다. 예!

Binary Search

룰루,, 이 알고리즘을 들고 Gold 3 난이도에 같은 제목, 같은 내용인 12738번에 제출하면 가차없이 시간 초과가 뜬다.

솔직히 알고리즘 문제를 해결하면서 '아 이건 이진 탐색이 들어가면 좋겠다!' 싶었던 때가 많이 없었는데, 한참 헤메다가 풀이를 보고 나서 문제를 보는 시각이 아주아주 약간은 넓어진 것 같다.

bisect

문제를 풀기 전에 Python의 내장 라이브러리인 bisect의 주요 기능을 먼저 정리해보자. 물론 직접 구현할 줄도 알아야겠지만, 쓰라고 준건데 써줘야 하지 않겠나! 호호!

bisect는 ~~말 그대로 이진 탐색을 구현한 파이썬 내장 라이브러리이다.~~ (<- 이건 아래서 정정하겠다!) 사용하는 패턴이 heapq와 비슷한데, 이진 탐색을 위한 클래스가 따로 제공되는게 아니라 len과 get item 연산이 지원되는 특정 객체와 탐색할 요소를 인자로 넘겨주는 방식이다.

아래는 bisect.bisect_left에 대한 VSC 설명이다.

이게 어떻게 작동하는건지 구체적으로 생각해보고 싶으면 Duck typing과 관련된 글을 찾아서 읽어보자.

여기서 눈치챘겠지만 해당 모듈은 인자로 받는 시퀀스가 정렬되어 있음을 가정한다. 정렬되어 있지 않은 상태로 인자를 넘겨주면 그냥 이상한 값을 반환 받는다는 뜻이지,,

구체적인 실행 결과는 다음과 같다.

from bisect import bisect_left

arr = [10, 20, 30, 40, 50, 60]

# 존재하는 값 : 0
find_10 = bisect_left(arr, 10)
print(find_10)

# 존재하는 값 : 5
find_60 = bisect_left(arr, 60)
print(find_60)

# 존재하지 않는 값 : 2
find_35 = bisect_left(arr, 35)
print(find_35)

# 존재하지 않는 값 : 0
find_minus_1 = bisect_left(arr, -1)
print(find_minus_1)

# 존재하지 않는 값 : 6
find_70 = bisect_left(arr, 70)
print(find_70)

만약 사용 방법을 알고 있다면 다음 절로 넘어가도 된다.

사실 생각 없이 bi,, 어쩌구니까 binary search를 구현했겠구나 싶었는데 결과를 정리하면서 뭔가 이상하단 생각이 들었다. 진짜 탐색이었으면 시퀀스에 없는 결과일 경우 -1이나 에러를 뱉어야 하는데 그것도 아니고, 애초에 이름부터가 bisect로 binary search를 줄였다기엔 어색하다.

그래서 찾아봤는데 이분법(Bisection algorithm)을 구현한 모듈이라고 한다. 그럼 그렇지!
위키피디아에 의하면, 이분법은 다음과 같이 정의된다.

수학에서 이분법(二分法, Bisection method)은 근이 반드시 존재하는 폐구간을 이분한 후, 이 중 근이 존재하는 하위 폐구간을 선택하는 것을 반복하여서 근을 찾는 알고리즘이다.

우리 케이스에 맞게 풀어서 설명하자면, 인자로 전달되는 시퀀스가 정렬되어 있음이 자명하므로 이진 탐색에서 그랬던 것처럼 지금 관심을 가지고 있는 구간의 정중앙의 값이 만약 탐색하려는 값이 아닌 경우 해당 값을 기준으로 더 작은 쪽(왼쪽)과 큰 쪽(오른쪽)으로 탐색 구간을 이분할 수 있다는 의미이다.

bisect_left는 결론부터 말하자면 이분법을 사용해서 특정 요소가 삽입되었을 때 정렬 상태가 깨지지 않는 위치를 반환한다. 일부러 좀 모호하게 설명을 덧붙였는데, 아래 예시를 한 번 보자.

arr = [10, 20, 30, 40, 50, 60]

idx_10 = bisect_left(arr, 10) # 0
arr.insert(idx_10, 10)
print(arr) # [10, 10, 20, 30, 40, 50, 60]

idx_25 = bisect_left(arr, 25) # 3
arr.insert(idx_25, 25)
print(arr) # [10, 10, 20, 25, 30, 40, 50, 60]

idx_70 = bisect_left(arr, 70) # 8
arr.insert(idx_70, 70)
print(arr) # [10, 10, 20, 25, 30, 40, 50, 60, 70]

보다시피 위의 경우 정렬 상태가 깨지지 않도록 10을 삽입하려면 0번 위치에 삽입해야 하고, 그럼 0번부터 맨 뒤까지 요소가 하나씩 밀린다.

마찬가지로 25를 삽입하려면? 20과 30의 사이에 삽입되어야 하므로 20과 30 사이, 인덱스 기준으로는 2와 3 사이에 삽입되면 된다. 그러므로 인덱스가 3인 부분에 삽입해서 30부터 그 뒷 숫자들을 하나씩 밀어주면 정렬 상태가 깨지지 않게 되는 것이다.

마지막 70의 경우 삽입 전 리스트의 길이가 8이므로 가장 마지막 요소의 인덱스는 7인데, 리스트에서 60이 가장 큰 수이므로 맨 뒤에 70을 삽입해야 한다. 그러므로 idx_70은 8이 된다.

물론 left가 있으면 right도 있어야겠지? bisect_left만 bisect_right로 바꿔서 결과를 확인해보자.


arr = [10, 20, 30, 40, 50, 60]

idx_10 = bisect_right(arr, 10)  # 1 <- 여기!
arr.insert(idx_10, 10)
print(arr)  # [10, 10, 20, 30, 40, 50, 60]

idx_25 = bisect_right(arr, 25)  # 3
arr.insert(idx_25, 25)
print(arr)  # [10, 10, 20, 25, 30, 40, 50, 60]

idx_70 = bisect_right(arr, 70)  # 8
arr.insert(idx_70, 70)
print(arr)  # [10, 10, 20, 25, 30, 40, 50, 60, 70]

25와 70에 대해서는 결과가 같은데, 맨 첫 요소인 10에 대해서는 결과가 다르다. 두둥,,

뇌 빼놓고 결과만 놓고 보면 arr에 포함되어 있는 값을 인자로 줄 경우 값이 달라지는 것 같은데, 아래 상황을 놓고 비교해보자.

arr = [10, 20, 30, 40, 50, 60]

# 0
idx_left_10 = bisect_left(arr, 10)
print(idx_left_10)

# 1
idx_right_10 = bisect_right(arr, 10)
print(idx_right_10)

# 2
idx_left_30 = bisect_left(arr, 30)
print(idx_left_30)

# 3
idx_right_30 = bisect_right(arr, 30)
print(idx_right_30)

~~좌우 대립~~

left와 right가 서로 다른 값을 반환하는데, 어떻게 된 일일까? 어느 쪽이 맞는 말을 하고 있는거지?

..둘 다 맞다! 왜냐하면, idx_left_10에 10을 삽입해도 10부터 맨 뒤까지 밀리기 때문에 순서가 맞고, idx_right_10에 10을 삽입해도 20부터 맨 뒤까지 밀리기 때문에 순서가 맞다.
idx_left_30과 idx_right_30도 마찬가지로 각각의 인덱스에 30을 삽입해도 20부터 60까지, 30부터 60까지 밀려 순서가 맞다.

이를 통해 만약 삽입 가능한 위치가 특정 요소 위치의 양옆일 경우, 둘 중 어느쪽을 반환할건지 차이만 있음을 알 수 있다.

더 알아보기

문제 풀이만 보려면 다음 장으로 넘겨도 좋다. 그냥 겸사겸사 알아두면 좋을 것 같아서 bisect 모듈의 다른 메서드까지 어떻게 작동하는지 한 번 보려고 한다.

좌우가 있다면 중앙도 있어야겠지? 실제로 bisect.bisect 함수가 있다.

여기서 잠깐! 위의 left, right 탐색에 대해서는 lo, hi 인자를 따로 주지 않았는데 이건 그냥 탐색 구간을 결정하는 값이다. 따로 주지 않았기 때문에 시퀀스의 전구간을 대상으로 탐색을 시작한건데, 만약 그럴 필요가 없으면 해당 값을 조정해주면 되겠다.

여하튼 bisect.bisect는 어떻게 작동할까? 묶어서 한 번에 보자.

from bisect import bisect_left, bisect_right, bisect

arr = [10, 20, 30, 40]

left_10 = bisect_left(arr, 10)
mid_10 = bisect(arr, 10)
right_10 = bisect_right(arr, 10)
print(left_10, mid_10, right_10) # 0 1 1

left_20 = bisect_left(arr, 20)
mid_20 = bisect(arr, 20)
right_20 = bisect_right(arr, 20)
print(left_20, mid_20, right_20) # 1 2 2

left_40 = bisect_left(arr, 40)
mid_40 = bisect(arr, 40)
right_40 = bisect_right(arr, 40)
print(left_40, mid_40, right_40) # 3 4 4

left_25 = bisect_left(arr, 25)
mid_25 = bisect(arr, 25)
right_25 = bisect_right(arr, 25)
print(left_25, mid_25, right_25) # 2 2 2

보면 알겠지만 bisect_right와 동일하게 작동한다. 개인적으로 bisect와 bisect_right가 같은 작동을 한다면, 가독성을 위해 후자를 써주는 편이 좋다고 생각한다. 어떤 의도를 가지고 이 코드를 작성한건지 코드만 보고도 가늠할 수 있도록 하는게 최고!

또한 위의 예제에서 list.insert 메서드를 썼던 데서 유추할 수 있다시피 아예 삽입까지 원큐로 수행해주는 기능 역시 존재한다.

사용 방법은 인덱스 반환 함수를 잘 이해하고 있다면 너무 직관적이라 더 설명할게 없는데, O(log n) 검색이 느린 O(n) 삽입 단계에 가려짐에 유념하십시오. 부분을 잘 읽어봐야 한다. 대개 그렇지만 Python list의 삽입 연산은 해당 위치의 뒤쪽에 있는 요소들을 한칸씩 뒤로 밀어주는 방식이기 때문에 O(N)의 시간 복잡도를 가지기 때문으로, 탐색이 아무리 빨라봐야 이 태생적인 한계는 어떻게 해줄 수 없다는 의미이다.

그래서, 코드!

길었다. 12015번을 풀어보자!

여러 글을 찾아봤는데 개인적으로 이 분의 글에 가장 설명이 잘 되어 있는 것 같아 코드부터 해설까지 많이 참고했다. 내 포스트로 부족하다 싶으면 저 분 블로그를 한 번 읽어보시는걸 추천한다!

from bisect import bisect_left

def solution(arr: List[int]):
    LIS = [arr[0]]

    for base_num in arr[1:]:
        if LIS[-1] < base_num:
            LIS.append(base_num)
        else:
            insert_idx = bisect_left(LIS, base_num)
            LIS[insert_idx] = base_num

    return len(LIS)

아름답다. 우아하게 논리를 담아냈다.
..그렇지만 많은 명작이 그러하듯 숨은 의미는 조금 난해하다. 살살 뜯어보자,,

해설

풀이에 앞서 함수의 반환 부분을 먼저 비교해보자.

앞의 S2 난이도 풀이에서는 반환 값이 max(dp)인 반면, 뒤의 G2 난이도 풀이에서는 len(LIS)이다. 전자는 O(N)의 시간 복잡도를 가지는 반면, 후자는 Duck typing 덕분에 O(1)이다. (잘 설명된 글이 있어 따로 설명 않겠다.)

이는 즉, LIS의 최대 길이라는 값의 모든 기록을 보려는게(O(N)) 아니라 반복에 의해 축적된 맨 마지막 상태(O(1))인 길이만 보려고 하겠다는 의미와 같다. 이 부분에서 감탄했다. 뭐랄까 PS적인 사고력이 이런걸 얘기하는거구나 싶어서,,

알고리즘의 세세한 작동 원리를 보기 전에 실눈뜨고 큰 개요만 보자면, arr에 대해 순회하는 루프 안에서 bisect_left가 호출되고 있으므로 이 풀이의 시간 복잡도는 O(N*logN)임을 알 수 있다. 루프가 하나 줄었으니 N이 logN이 된 것이다. 어떻게 가능한걸까?

루프를 시작하기 전 LIS에는 arr의 맨 앞 요소만 담긴다. 이건 문제 조건에 arr의 길이가 1 이상으로 정의되었으므로 별 고민 없이 해도 된다. 길이가 1인 배열의 경우 LIS 역시 같은 값을 가지는 배열이기 때문이다.

여기서 눈치챘겠지만 LIS는 말 그대로 LIS의 조건을 계속 만족할 것이다. 그렇기 때문에 base_num에 대한 반복이 끝난 후 len(LIS)를 반환한게 곧 정답이 된다.

그림을 그려보자. 단, 문제와 arr 값을 살짝 다르게 조정했다.

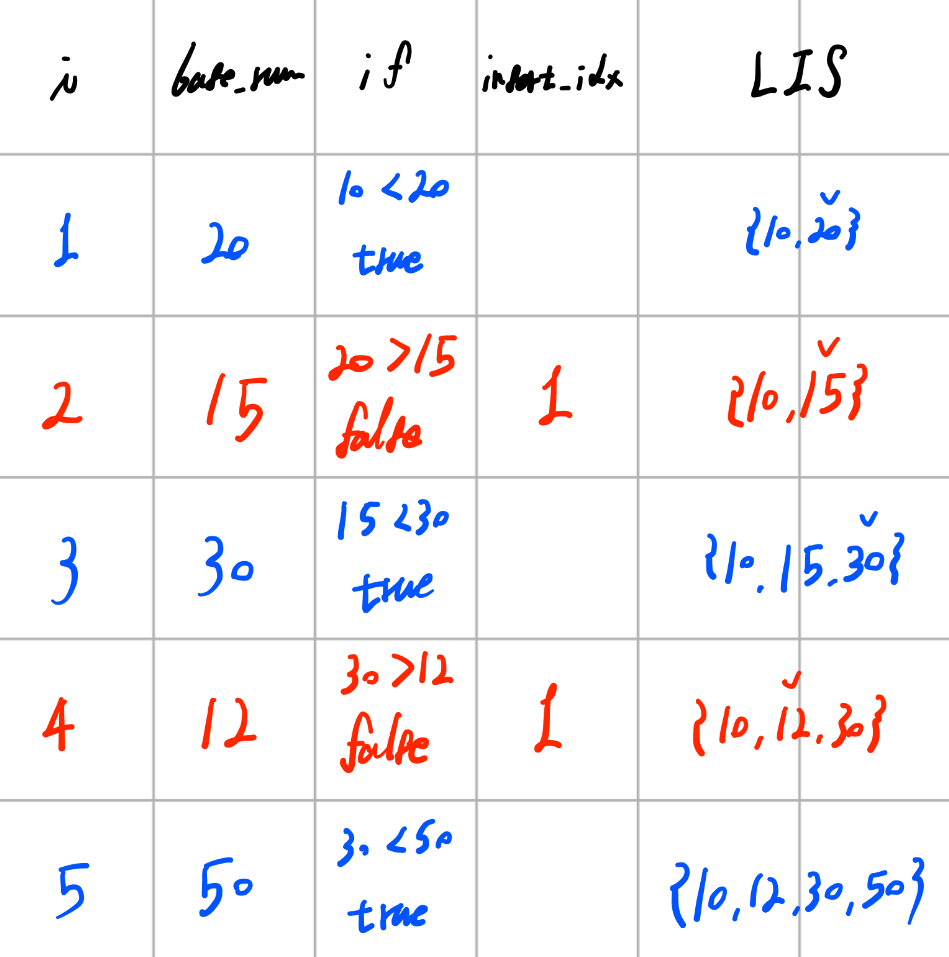
파란색 부분은 if문에서 True로 통과된 경우, 빨간색 부분은 else문으로 빠진 경우이다.

한 줄씩 보자면,,

i	base_num	if	insert_idx	LIS
0				{10}

이건 초기 상태이다. 위에서 언급했듯 길이가 1인 배열은 해당 배열의 LIS와 같은 모양임을 명심하자.

i	base_num	if	insert_idx	LIS (after)
1	20	10 < 20 (true)		{10, 20}

i가 1, base_num이 20인 상황으로, 크게 고민할 것 없이 LIS의 맨 끝값이 10으로 20보다 작기 때문에 LIS의 끝에 그대로 추가해 주어도 LIS는 여전히 LIS의 조건을 만족한다.

i	base_num	if	insert_idx	LIS (after)
2	15	20 > 15 (false)	1	{10, 15}

짜잔,, 여기부터 흥미롭다. 15는 LIS의 맨 끝 수인 20보다 작으므로 뒤에 바로 추가할 수 없는 것까지는 너무 당연한데, 15가 들어갈 자리를 찾아 해당 자리에 15를 써버렸다. 그 결과 LIS의 끝 수는 20에서 15가 되었는데, 이렇게 값을 덮어 써도 LIS는 여전히 조건을 만족한다. 이게 과연 문제가 없을까?

없다! 만약 LIS가 여러개일 수 있어서 모든 경우를 모두 반환해야 한다면 다른 풀이가 필요하겠지만, 최소한 여기서는 LIS 자체가 아닌 LIS의 최대 길이라는 상태를 필요로 하기 때문에 상관이 없는 것이다.

이게 왜 가능한건지 위에서 '잘 설명된 글'이라고 링크를 걸어놓은 분의 해설을 옮겨보자면,,

다음 훑는 원소가 LIS 수열의 마지막 원소보다 작은 경우, LIS 수열을 이루는 원소 중 탐색 원소와 '가장 차이가 안나면서 더 큰' 원소를 찾는다.

"우리는 현재 LIS 구성 상태에 관심있는 것이 아니라, 그 길이에 관심이 있다. 즉, 이 '대체'는 '현재까지의 LIS 길이를 보전하면서, 동시에, 미래의 새로운 LIS가 생기는 것을 대비하기 위함이다.

또 다른 분께서 잘 설명해놓으신 부분을 같이 보면 더 이해가 잘 된다.

LIS, 즉 가장 긴 증가하는 부분 수열이라함은 결국 중점이 '증가' 한다는 것과 '가장 길다' 는 것이다.

증가한다는 것은 선행 원소보다 후행 원소가 커야한다는 것이고, 가장 길다는 것은 제한 된 수의 범위 내 볼 때 상호 원소간 값의 차이가 적어야한다는 의미다.

그러나 앞서 필자가 두 가지 키워드를 말했었다. 그 중 하나가 바로 상호 원소간 값의 차이가 적어야한다는 것이다. 그래야 최대한 많이 배치할 수 있으니깐 말이다.

그럼 어떻게 해야할까?
바로 좀 더 작은 값으로 큰 값을 대치하는 것이다. 좀 더 풀어서 말하면 탐색 값보다 큰 값중 가장 가까이에 있는 수와 맞바꾼다는 것이다.

공통적으로 '가장 차이가 적은' 값을 찾아 기존의 값을 대치한다는데, 결과만 놓고 보자면 LIS는 이미 정렬되어 있음이 보장되기 때문에 선형 탐색을 통해 후보를 찾을 필요가 없다. 위에서 살펴본 bisect를 활용한 이분 탐색 기법을 사용하면 시간 복잡도를 O(N)에서 O(logN)으로 개선할 수 있다는 의미이다.

그럼 이 풀이의 핵심, 왜 가장 차이가 적어야 하며, 왜 대체해도 문제가 없다는걸까?
우리 예시의 경우 {10, 20}의 맨 끝인 20이 15보다 큰 수 중 가장 작은 수였으므로, 이 값을 15로 대체하여 {10, 15}가 되었다. 만약 이걸 갱신하지 않고 그냥 끌고 간다고 가정하고, 음,, 잠깐 15와 20 사이의 값인 17을 삽입해보자.

우선 대체하지 않을 경우 다음과 같다.

i	base_num	if	insert_idx	LIS (after)
3	17	20 > 17 (false)	1	{10, 20}

따로 대체가 발생하지 않기 때문에 i=3에 대한 반복을 마쳐도 여전히 LIS는 {10, 20}이다.

반면 대체가 발생할 경우 아래와 같다.

i	base_num	if	insert_idx	LIS (after)
3	17	15 < 20 (true)		{10, 15, 17}

결과를 놓고 보면 후자가 옳다. {10, 15, 20, 17}의 최대 길이 LIS는 {10, 15, 17}이니까!

또 다른 예시로, {10, 15, 20, 5}을 각각 대체가 발생할 때와 아닐 때로 나누어 생각해보자.

대체하지 않을 경우 다음과 같다.

i	base_num	if	insert_idx	LIS (after)
3	5	20 > 5 (false)	1	{10, 20}

마찬가지로 5가 끼어들 구석이 없다. 반면 대체가 발생할 경우 아래와 같다.

i	base_num	if	insert_idx	LIS (after)
3	5	15 > 5 (false)	0	{5, 15}

5을 삽입하기 전의 LIS는 대체가 발생하여 {10, 15}였고, 삽입 후에는 {13, 15}가 되었다.

위의 설명과 결과를 풀어서 정리하자면, 대체를 통해 LIS의 조건을 만족시키면서 이후 원소가 더 많이 들어올 수 있도록 해준 것이라 할 수 있겠다. 대체되어도 bisect_left 특성상 LIS 규칙을 깨지 않으며, 우리가 궁금한 것은 LIS의 요소 하나하나가 아닌 LIS의 최대 길이이므로 다음 LIS를 결과값이 아닌 다음 LIS를 더 효율적으로 구하기 위한 부가 정보로 생각하자는 의미이다.

물론 base_num에 대한 순회를 마친 후 LIS가 조건을 만족하기는 하지만, 궁극적으로 궁금한 것은 가능한 LIS의 최대 길이이기 때문에 이러한 접근이 유효할 수 있다.

bisect_right는 웨안되?

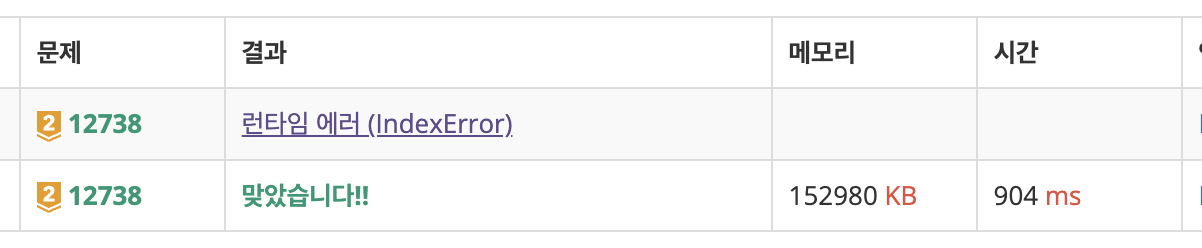
더 깊은 이해를 위해 bisect_left를 bisect_right로 바꿔서 제출해보면 위와 같이 IndexError가 뜬다.

이건 먼저 예시를 보면 좋을 것 같은데, arr을 [10, 10]으로 놓으면 바로 이유가 나온다.

i	base_num	if	insert_idx	LIS (after)
1	10	10 == 10 (false)	1	IndexError

보이는가! bisect_right는 해당 위치에 값을 삽입해도 정렬 상태가 깨지지 않는 오른쪽 위치를 반환한다. 만약 bisect_left를 썼다면 1이 아닌 0이 반환되었을 것이므로 그냥 LIS의 첫 요소가 (무의미하게) 같은 값인 10으로 대체되었겠지만, 여기서는 1이 반환되었기 때문에 LIS의 길이 바깥의 위치인 1에 접근하여 IndexError가 발생한 것이다.