어제 Base & Bound 기법을 통해 프로세스가 사용할 가상의 주소 공간을 실제 물리 메모리에 옮기는 방법을 공부했는데, 끝에서 얘기했다시피 Base & Bound 기법에는 Internal Fragmentation 문제가 있다.

저어기 32~48KB 구간을 보면, Heap과 Stack 사이 영역이 전혀 사용되고 있지 않은데도(allocated but not in use) 프로세스가 이 메모리 공간까지 점유하여 낭비가 되고 있는데, 이걸 Internal fragmentation이라고 한다. 내부 단편화!
또한 지난 장에서 세운 가정인 '주소 공간이 물리 메모리보다 큰 경우'에도 대처할 수 없는 구조이다. 만약 한 프로세스에게 주어지는 주소 공간이 위의 64KB 메모리에 연속적으로 할당할 수 없는 100KB라면 Base & Bound 방법으로는 Memory Virtualization이 불가능하다. (물론 주소 공간만 100KB이고, 실제로 사용되는 데이터는 물리 메모리의 가용한 공간보다는 적어야 하겠지만,, 이마저도 나중엔 디스크의 swap 영역을 통해 극복한다.)
책에는 이걸 Base & Bound 기법이 유연성이 없다고 표현했는데, 오늘 배울 Segmentation은 얼마나 쫄깃쫄깃할지 한 번 뜯어보자!

16.1. Segmentation: Generalized Base/Bounds
이런 Base & Bound의 뻣뻣함을 해결하기 위해 고안된 Segmentation 기법을 아래와 같이 설명할 수 있다.
일단 Segment란, 주소 공간 안에 포함되는 특정 길이의 연속적인 주소 공간으로 정의할 수 있다.
이는 주소 공간의 시작 주소와 끝 주소를 기록하는 Base & Bound 방식과 다르게 주소 공간 안에 더 작은 단위(Segment)를 만들어서, 각각의 단위에 해당하는 주소 공간을 표현하기 위한 시작 주소, 끝 주소를 Segment마다 두어 관리하겠다는 것이다!
이 Segment는 Code, Stack, Heap의 세 종류가 있어 이전과 달리 굳이 이 세 덩어리를 저장하기 위해 물리 메모리 상에 연속적으로 배치할 필요도 없고, 위의 Internal Fragmentation 같은 낭비가 발생할 일도 없다.
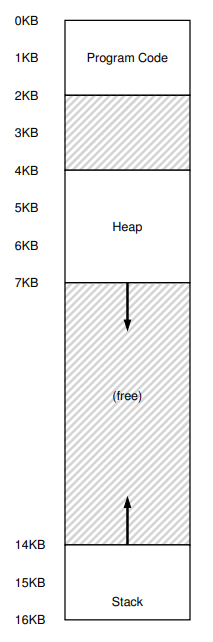
만약 위와 같은 주소 공간을 이전의 방법으로 물리 메모리 위에 올려준다면, 쓸데없이 사용되고 있지 않은 2~4KB, 7~14KB, 총 9KB.. 절반 이상의 영역이 사용되지도 않은 채로 멀뚱멀뚱 낭비되었을 것이다.


그런!데! Code, Heap, Stack을 저장하기 위해 메모리를 연속적으로 할당하지 말고, 위와 같이 각 Segment에 Base와 Bound를 두어 따로 관리해주면, 전에 발생했던 Internal Fragmentation이 사라졌음을 확인할 수 있다. 심지어 메모리가 위치하던 순서도 주소 공간과 물리 메모리가 서로 다르다.
위와 같이 사용되지 않는 구간이 많은 듬성듬성한 메모리 공간을 Sparse address space라 하는데, 메모리가 알뜰하게 잘 쓰이고 있는 상황이었어도 그렇겠지만 빈 공간이 많은 이런 sparse address space에서는 internal fragmentation이 정말 뼈아플 것이다.
참고로 저 Segment를 나눈 기준은 막 정한 것이 아니라, 주어진 주소 공간을 절반씩 나누어 경계를 정하는 것이라고 한다. 예를 들어 2구간으로 주소 공간을 Segment로 분리하면 0~8KB, 8~16KB의 두 세그먼트가 나오는 것이고, 이걸 또 절반으로(2^2) 분리하면 0~4KB, 4~8KB, 8~12KB, 12~16KB의 네 세그먼트가 나오는 것이다.
아래서 다루겠지만 이 각각의 Segment 구간을 표현하기 위해 2^n개의 Segment를 가지는 주소 공간에서는 n bit가 필요한데, 위와 같이 Code, Heap, Stack의 세 Segment를 표현하기 위해 주소 공간을 최소 4개의 Segment로 분할해야 하므로, 2bit를 사용해 각각의 Segment를 아래와 같이 표현할 수 있다.
| Segment 번호 | 시작 주소 | 끝 주소 | 용도 |
|---|---|---|---|
| 00 | 0KB | 4KB | Code |
| 01 | 4KB | 8KB | Heap |
| 10 | 8KB | 12KB | 미사용 |
| 11 | 16KB | 12KB | Stack |
처음에는 Stack이 좀 의아했는데(그래서 주소 변환 방법도 쪼금 다르다), Stack이 Heap과 반대 방향으로 성장한다는 사실을 생각하면서 아래 주소 변환 예제를 풀어 보면 슥 이해할 수 있을 것이다. 호호!
Segmentation에서의 주소 변환
Base & Bound의 일반화된 형태가 Segmentation이므로, 가상 주소를 실제 메모리 주소로 변환하는 주소 변환 역시 비슷한 방법으로 이루어진다.
Code Segment에서의 주소 변환
위의 예제에서 가상 주소 100B에 접근하는 코드가 있다면, 일단 이 메모리 접근이 정해진 영역을 벗어나지는 않는지부터 확인해야 한다. 여기서는 0~2KB 구간이 Code 영역(00)이므로 다른 영역을 침범하고 있지 않으니, 위의 Segment Table을 참고하여 가상 주소 100B가 포함된 코드 영역의 Base인 32K에 100B만큼 더해준 32,868B가 실제 물리 메모리 주소가 된다.
Base & Bound 기법에서 주소 변환을 수행하기 전에 이미 점유되고 있는 메모리 공간에 접근하려는 시도가 있을 경우 Out of bounds 예외가 발생한다고 했는데, 여기서도 마찬가지로 각각의 Segment에 Base, Size 쌍이 있어 이 범위를 침범하는 메모리 접근이 있을 경우 그 유명한 Segmentation Fault가 발생하게 된다.
💡Heap Segment에서의 주소 변환💡
Code 영역은 Base & Bound와 같은 방법으로 주소 변환이 되어서 놓치기 쉬운데, 그렇다고 해서 주소 공간을 Segment로 나누지 않고 연속된 메모리 공간으로 생각하고 계산하면 Heap의 주소 변환을 잘못 계산하게 된다.
예를 들어 가상 주소 공간의 4200B에 해당하는 주소가 Heap Segment(01)에 포함되므로, 그냥 Heap의 Base인 34K에 4200B를 더하면 될 것 같지만 참조하려는 4200B이 Heap Segment의 Base로부터 얼만큼 떨어져 있는지를 계산하여 Offset으로 사용해야 한다.
물리 주소를 알고 싶은 4200B가 주소 공간 안에서 Heap Segment의 Base인 4096B로부터 104B만큼 떨어져 있으므로, 주소 변환시 물리 메모리에서 Heap Segment의 Base인 34KB에 Offset 104B를 더한 34,920B가 주소 변환의 결과가 된다.
💡Stack Segment에서의 주소 변환💡
아래 16.3절에서 다뤄보겠다. 기대하시라!
16.2. Which Segment Are We Referring To?
이 좋은 Segment를 컴퓨터에서는 어떻게 표현하고 다룰 수 있을까? 14bit 길이의 가상 주소를 가정해보자.
위에서 이미 얘기하긴 했는데, 이 경우 3개의 Segment가 필요하고, 주소 공간을 반씩 나누어 Segment로 분리하는 것이므로 최소 4개의 Segment로 나누어져야 하기 때문에 이를 2bit를 사용해 주소 공간을 아래와 같이 표현할 수 있다.
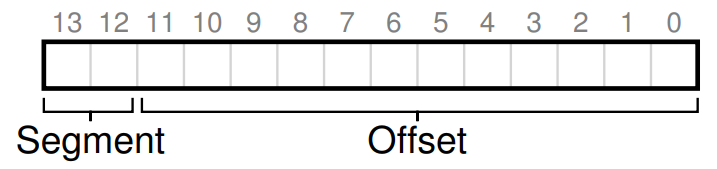
저 상위 2bit의 Segment bit가 바로 주소 공간 안에서 segment를 구분하기 위한 성분이고, 아래 Offset은 Segment Base로부터 얼만큼 떨어져 있는지 표시하기 위한 bit이다.

예를 들어 위와 같은 주소 공간(10진수로 4200에 해당)은 아래와 같이 주소 변환된다.
- Segment bit가 01이므로, Heap Segment 내부의 주소를 의도한 것임을 알 수 있다.
- 또한 Offset이 1101000(2) = 8 + 32 + 64 = 104B임을 알 수 있다.
- 어차피 Offset은 Base로부터 얼만큼 떨어져 있는 지점의 주소인지를 나타내기 위한 것이므로, Segment table을 참고해 Bound보다 작은지만 검사해주면 된다. 따라서 Bound 값이 3KB였으므로, 여기선 Segmentation fault가 발생하지 않는다!
- Heap Segment의 물리 메모리에서 Base가 34KB임을 알고 있으므로, 34KB + 104B = 34,920B가 주소 공간에서 4200B에 대응하는 위치임을 계산해냈다! 와!

이 주소 변환 작업은 CPU의 MMU에서 수행되는데, 위의 수도 코드의 의미는 다음과 같다.
- 2) 여기서 VirtualAddress는 10진수 4200의 binary bit 표현으로, SEG_MASK가 0x3000 = 0011 0000 0000 0000이므로 (VirtualAddress & SEG_MASK)는 12, 13번째 bit를 제외한 나머지 bit를 모두 0으로 바꿔준 값이다.
다음으로 이 Segment bit만 남은 bits를 SEG_SHIFT, 그러니까 12만큼 오른쪽으로 Shift 해주면? 0000 0000 0000 0001과 같이 오른쪽으로, 낮은 자리로 Segment bit가 밀리게 된다. - 4) Offset 역시 마찬가지로, OFFSET_MASK가 0000 1111 1111 1111이므로 (VirtualAddress & OFFSET_MASK)는 Segment bit는 사라지고 Offset만 남긴 0000 0000 0110 1000과 같은 형태로 변환된다.
- 5) Bounds[Segment]가 해당 Segment의 Bound 크기를 의미하므로, 만약 여기서 구한 Offset이 이 경계 주소에 걸쳐 있거나 그보다 큰 경우 허락되지 않은 다른 메모리에 침범하는 것과 마찬가지이므로 PROTECTION_FAULT를 발생시킨다.
- 6) 만약 접근하려는 주소가 다른 영역을 침범하지 않은 유효한 접근이라면, 위에서 해봤던 방법 그대로 해당 Segment의 Base 값에 Offset을 더해 실제 물리 메모리에 접근하면 된다!
Segment 표현에 관한 여러 이슈들
어째 Internal fragmentation을 없애보려고 위와 같이 주소 공간을 Segment로 분리해서 따로 관리한건데, 3개의 Segment를 위해 주소 공간을 4분할하게 되면 아까부터 신경쓰이던 Segment 10에 해당하는 25%의 메모리 공간은 계속 놀게 되기 때문에, 어떤 시스템에서는 Code Segment와 Heap Segment를 하나로 합친 Segment와 Stack Segment만 사용해 1bit로 각각의 Segment를 구분하기도 한단다.
또,, 필요 이상으로 Segment를 여러 개 사용하게 되면, 사용할 수 있는 주소 공간의 크기가 한정되어 있으니 Segment 개수에 반비례하여 각각의 Segment Size가 작아질 수 밖에 없다. Code Segment야 프로그램 실행 도중에 크기가 변할 리가 없으니 프로세스 시작 전에 적당한 크기를 정해주면 되지만, Stack과 Heap Segment는 얼만큼 크기가 늘어날지 알 수 없기 때문에 너무 많은 Segment로 주소 공간을 분리하지 않도록 주의해야 할 것이다.
오 이건 좀 신선한데, 위의 방식처럼 Explicit하게 Segment bit를 사용해 각 segment를 구분하는 것이 아니라 예를 들어 주소가 PC에서 생성(Instruction fetch)되었다면 이 주소를 Code segment 내부에 있는 것으로 보고, Stack/Base Pointer를 기준으로 생성되었다면 Stack segment, 이외의 주소는 Heap segment에서 생성된 것으로 취급하는 등 HW를 사용한 Implicit한 접근 방식도 있다고 한다.
16.3. What About The Stack?

위의 Segment Table에서 봤다시피, Stack segment의 Base와 메모리 성장 방향은 Code, Heap Segment와 반대로 되어 있다.
사람이야 그냥 '아~~ 반대로 되어 있구나~~' 하고 생각할 수 있는데, 시키는 것밖에 못하는 바보 멍충이 컴퓨터는 이 '반대'라는 개념을 명시적인 값으로 알려주어야 한다.

아까 봤던 Segment Table에 'Grow Positive?' Column이 추가되었는데, 이 값이 1이면 메모리가 양의 방향으로 커지고, 0이면 메모리가 음의 방향으로 커지는 것을 의미한다.
이 정보를 가지고, 하드웨어는 아래와 같이 주소 변환을 수행한다.
💡Stack Segment에서의 주소 변환💡
Heap이나 Code Segment와는 달리, Stack Segment의 Grows Positive? bit가 0이므로 아래와 같이 주소 변환을 수행해 주어야 한다.
예를 들어 주소 공간에서 Stack 영역에 속하는 15KB 주소에 접근한다고 생각해보자. Stack의 시작 지점이 낮은 자리가 아니라 높은 자리이기도 하고, 메모리가 크는(?) 방향도 반대여서 좀 헷갈릴 수도 있는데 Heap segment와 마찬가지로 그냥 Stack Segment의 Base로부터 얼만큼 떨어져 있는지를 생각해보고 계산하면 된다.
위에서 16KB 주소 공간을 4개의 Segment로 나누어 Stack segment(11)의 Base를 16KB(12KB 아니다!)로 정했으니, 15KB이 16KB로부터 -1KB만큼 떨어져 있으므로 Offset을 -1KB로 생각하면 된다. 그럼 물리 메모리에서 Stack segment의 Base가 28K이므로, 여기에 -1KB를 더해주면 27KB로 주소 변환이 완료된다. 휴!
16.4. Support for Sharing
전에 Process API에서 fork() System call을 통해 자신과 동일한 자식 프로세스를 생성할 수 있음을 배웠는데, 이 경우 exec() System call을 통해 아예 다른 프로세스로 전환되지 않는 이상 부모 프로세스와 자식 프로세스가 같은 Code 영역을 공유해도 상관이 없다. 오히려 좋다! 같은 정보를 두 번 저장하지 않는다는 얘기니까.
Code 영역은 프로그램 실행 중에 읽기(r), 쓰기(w), 실행(x) 중 읽기(r)와 쓰기(x)만 가능하다는 전제 하에 프로세스끼리 공유할 수 있는 것인데, 이를 좀 더 일반적으로 정의하기 위해 HW에 Protection bit를 추가하여 아래와 같이 표현할 수 있다.
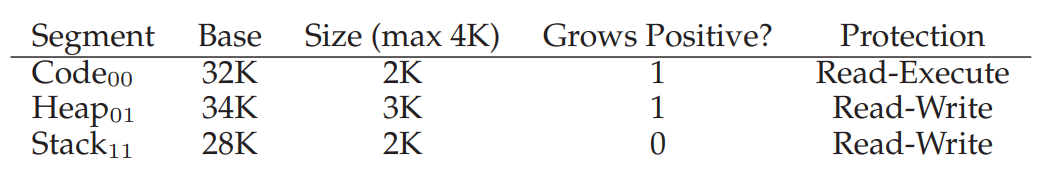
이렇게 명시적으로 Code segment에 Write가 불가능하다고 달아주면, 다른 프로세스가 이 메모리에 접근하던가 말던가 고민할 필요 없이 나만 이 Segment에 접근하고 있는 것처럼 그냥 사용할 수 있게 되는 것이다.
물론 Read만 가능한 Segment에 Execute나 Write를 수행하려는 등의 잘못된 접근을 막기 위한 추가적인 Trap Handling logic 역시 추가되어야 할 것이다.
16.5. Fine-grained vs Coarse-grained Segmentation
Fine-grained Segmentation은 말 그대로 주소 공간을 잘게 나누는 것이고, Coarse-grained Segmentation은 거칠게, 뭉텅뭉텅 주소 공간을 나누는 것을 의미한다. (방금까지 살펴본 4개의 4KB Segment로 나눈 상황이 coarse-grained segmentation이라 할 수 있다.)
둘 다 장단점이 있는데, Segmentation을 작게, 많이 나누게 되면 아무래도 메모리를 작은 단위로 좀 더 유연하게 조작할 수 있지만 이걸 일일이 관리하는게 더 어려워지고, Segmentation을 크게, 조금 나누게 되면 Segmentation의 수가 줄어 관리는 편해지지만 반대로 유연성이 좀 떨어지게 된다.
16.6. OS Support
Base & Bound가 주소 공간을 연속적으로 프로세스에 할당해주는 바람에 Internal fragmentation이 발생했던 문제를 Segmentation에선 각 segment가 독립적으로 base와 bound를 가지게 하여 해결했었는데, 위에서 MMU 내부의 주소 변환 Mechanism을 다루었으니 이번엔 segmentation을 지원하려면 OS가 어떤 것을 지원해야 할지 생각해보자.
첫째로, Base & Bound 방법과 마찬가지로 Context switching시 이 주소 변환을 위한 정보, 여기서는 Segment table을 저장/복원하는 기능을 지원해야 한다. 아무래도 Base, Bound register 두 개만 저장하면 되는 Base & Bound 기법보다는 좀 더 관리할 대상이 많아질 것이다.
둘째로, Heap으로부터 메모리를 할당받는 malloc() API 등을 통해 segment의 일부를 떼어주는 기능과 동시에 할당받은 segment 이상으로 메모리가 커질 경우 UNIX의 sbrk() System call 등을 사용해 Heap segment 자체의 크기를 늘려줄 수 있는 등의 기능이 필요하다. 물론 물리 메모리 자체가 부족한 상황이나 너무 잦게 메모리 추가를 요청하는 경우에는 OS가 이 요청 자체를 거부해버릴 수도 있다.
마지막으로, Base & Bound에서의 Free list처럼 비어 있는 물리 메모리 공간을 관리하기 위한 방법이 필요하다. 이전과 다른 점이 있다면 빈틈없이 나누어져 있는 물리 메모리를 고정된 크기로 할당해주는 것이 아니라 Segment의 Size에 따라 각각 다르게 할당해주어야 한다는 것이다.
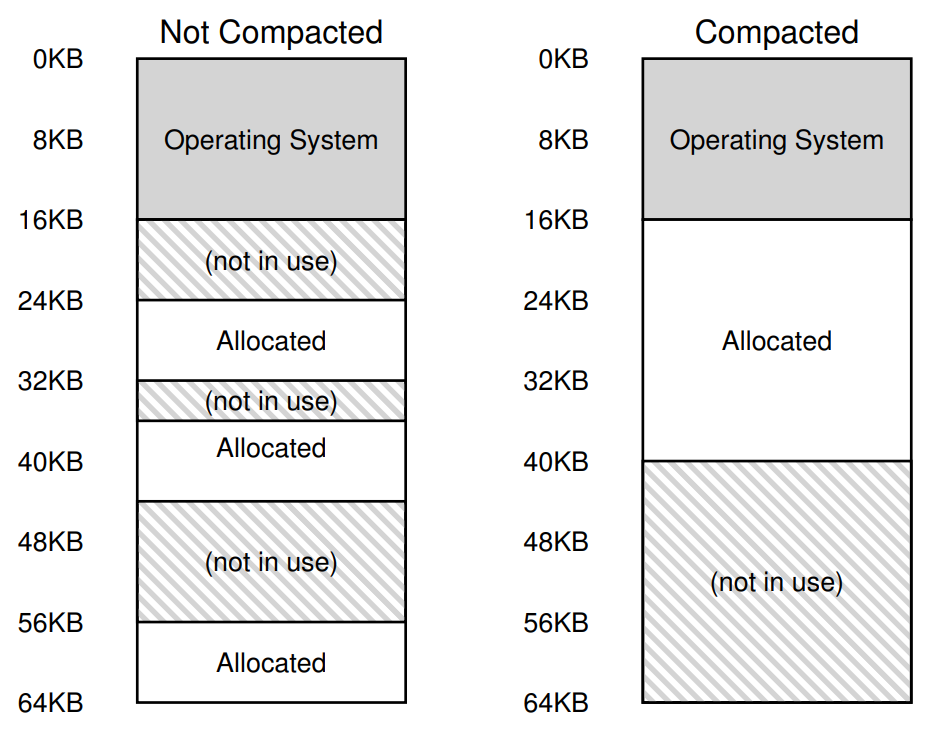
여기서 문제가 하나 발생하는데, 바로 External fragmentation이다. 뭔가 Internal fragmentation과 비슷할 것 같지 않은가?
Internal fragmentation이 연속적으로 할당된 메모리 내부에 사용하지 않는 자투리 공간이 남는 문제였다면, External fragmentation은 할당된 메모리 외부에 메모리 낭비가 발생하는 문제를 의미한다.
예를 들어 왼쪽의 Not Compacted 메모리 상태에서, 20KB만큼의 주소 공간을 요구하는 프로세스를 생성하려면 어떻게 해야 할까?
빈 공간을 다 합치면 24KB가 나오기는 하는데, 이게 20KB만큼 연속적으로 모여 있는게 아니라 20KB보다 작은 크기로 다 드문드문 떨어져 있기 때문에(이걸 chunk라고 한다) 다 모아 놓으면 충분히 프로세스에 메모리를 할당할 수 있음에도 불구하고 메모리 할당을 수행할 수 없다. 이게 외부 단편화, External fragmentation이다.
그럼 이 흩어져 있는 chunk들을 모아주면 될 것 아니겠는가!
따라서 OS는 이 흩어져있는 chunk들을 모아주는 Compact 기능을 제공해야 하는데, external fragmentation으로 인해 프로세스에 메모리를 할당할 수 없는 경우 방해가 되고 있는 프로세스를 잠깐 멈춘 뒤 다른 곳으로 치우는 방식(Segment 정보도 물론 갱신해주어야 하고!)을 반복함으로써 오른쪽과 같이 연속된 큰 물리 메모리 구간을 만들어내는 작업을 의미한다.
다만 이것도 공짜로 되는 작업이 아니고, 메모리를 통째로 다른 어딘가에 복붙하는 연산 자체가 매우 비용이 큰 일임을 명심해야 한다.
이게 좀 복잡하다 싶으면, 처음부터 빈 공간을 관리하기 위한 Free list를 사용하면 된다.
이때 빈 공간을 내어주는 알고리즘으로 best-fit, worst-fit, first-fit, buddy algorithm 등이 있는데, 다음 장에서 배울 것이다.
물론 이런 방법들을 사용한다고 해서 완벽하게 External fragmentation을 제거할 수는 없고(시스템을 만들 때부터 모든 프로그램에 대한 메모리 할당이 External fragmentation을 유발하지 않도록 한다고?), 이를 최소화하는 것을 목표로 해야 한다.
마무리
이번 장에서는 Base & Bound 방법에서 발생하는 Internal fragmentation 문제와 할당하려는 주소 공간이 물리 메모리보다 클 때 이에 대처할 수 없는 문제를 해결하기 위한 Segmentation 기법을 배웠다!
다만 Segmentation 방법으로 해결하지 못한 문제가 둘 남아있다.
첫째로, Segmentation 특성상 구간을 빈틈없이 일정한 구간으로 나누지 않고 가변 크기의 Segment로 분리했기 때문에 발생하는 External fragmentation 문제가 발생했다.
둘째로, 주소 공간이 듬성듬성 사용되는 Sparse address space에서 사용하기에는 아직 충분히 유연하지 못하다. 예를 들어 Heap segment를 크게 할당 받았는데 그 Heap이 듬성듬성 사용되고 있다면? 이 역시 공간 낭비일 것이다.
...
아휴. 지쳐. 혼자 피식피식 웃으면서 해보려고 전에는 어디서 요상한 사진도 줏어오고 그랬는데 지금은 기력이 없어서 그것도 힘들다 ㅋㅋㅋㅋㅋㅋㅋㅋㅋ ㅠ
약간,, 재밌는 시리즈 영화를 1편부터 500편까지 한 번에 몰아서 보는 기분이랄까,, 흥미롭고 즐거운데 분량이 너무 많아서 좀 괴롭다. 오늘 내일은 하나씩만 쓰고, 주말에 두개씩 써봐야겠다. 중간 시험 범위까지 6개 남았다! 아ㅏ아아ㅏㄱ!

