이분 탐색 박살내기 1 : BOJ 1920 수 찾기 (S4)

급식·2024년 6월 9일
Binary Searchps
0

알고리즘

목록 보기
8/12
post-thumbnail

알하,, 거의 9개월만에 쓰는 알고리즘 포스팅이구만.

저번에 정말 가고 싶었던 기업 면접도 떨어지고, 그 소식 듣자마자 모 기업 코테를 봤는데 멘탈이 아주 작살이 나버려서 한 문제도 손을 못댔다. 다 안되니까 너무 무기력해서 몇 일을 그냥 팽팽 놀았는데, 이렇게 살면 진짜 이렇게 끝날 것 같아서 잡페어 끝날 때까지 알고리즘 공부를 각잡고 해보려고 한다.

먼저 알고리즘 스터디에서 뽑아준 문제(BOJ 1300, K번째 수)를 하나 풀어보려는데 대강 제곱씩 줄여서(?) 풀면 되나보다 싶으면서도 도저히 풀이 방법이 생각이 안났다. 찾아보니 이분 탐색 응용 문제였고, 예전에 lower bound와 upper bound를 제대로 이해 못한 상태에서 얼렁뚱땅 넘어갔던 것 같아 아예 기본부터 다시 짚어보려고 한다.

마침 이분 탐색을 다루는 백준 문제집이 있어서 이걸 쭉 풀어볼건데, 다시 읽어봤을 때 전부 끄덕끄덕 하면서 읽을 수 있도록 최대한 쉽게 풀어서 써볼 것이다. 해보자 해보자!

접근 1 : Set과 visited 배열

말했다시피 S4 난이도의 수 찾기 문제이다. 가능하면 문제를 캡쳐하기 보단 링크를 올려줬으면 한다는 안내를 본 것 같아서 앞으로 가급적이면 링크만 올리려고 한다.

아무튼 S4 난이도인 만큼 문제 자체는 쉽다. 존재 여부를 확인해야 할 때 나는 제일 먼저 Set과 Boolean 배열을 떠올려왔는데, 가장 마지막 풀이를 보니 역시 아래와 같이 풀었었다.

구현 1 - Set을 활용한 풀이

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.HashSet;
import java.util.Set;
import java.util.StringTokenizer;

public class Main {
    static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    static StringBuilder out = new StringBuilder();

    public static void main(String[] args) throws Exception {
        final int ARRAY_LENGTH = Integer.parseInt(in.readLine());
        Set<Integer> set = new HashSet<>();

        StringTokenizer st = new StringTokenizer(in.readLine());
        for (int idx = 0; idx < ARRAY_LENGTH; idx++) {
            int num = Integer.parseInt(st.nextToken());
            set.add(num);
        }

        final int SEARCH_CNT = Integer.parseInt(in.readLine());
        st = new StringTokenizer(in.readLine());
        for (int idx = 0; idx < SEARCH_CNT; idx++) {
            int target = Integer.parseInt(st.nextToken());
            if (set.contains(target)) {
                out.append(1).append('\n');
            } else {
                out.append(0).append('\n');
            }
        }
        System.out.println(out);
    }
}

별 거 없다! 그냥 Set 자료형에 숫자를 넣어서 있는지 없는지 확인하는 코드고, 496ms에 60464KB를 썼다.

또 혹시나 Boolean 배열을 쓰는 풀이는 또 뭔가,, 싶은 사람이 있을까 싶어서 남기는건데 내가 알기론 이 방법으론 못 푼다. 흔히 DFS, BFS 같은 탐색 문제에서 특정 노드에 방문했는지 확인하기 위해 visited 같은 이름의 배열을 쓰는 방법과 동일한데, 우선 하나의 배열로는 불가능한게 정수가 [-2^31, 2^31) 범위 안에 있기 때문이다.

풀어서 설명하자면 4바이트의 int 타입이 표현할 수 있는 범위는 4바이트 = 32비트이므로 부호를 표현하기 위한 MSB에 1비트를 제외한 31비트를 부호를 제외한 숫자 표현에 사용할 수 있다. 따라서 [-2^31, 2^31-1], 즉 [-2^31, 2^31) 범위의 수만 표현할 수 있는데, 오른쪽에 붙은 -1은 0을 표현하기 위해 경계가 왼쪽으로 하나 줄어든 것으로 생각하면 된다.

또한 JVM 내부 구현 상 Long type 크기를 가지는 배열을 선언할 수 없기 때문에, [-2^31, 2^31) 범위를 하나의 배열로 존재 유무를 체크할 수 없음을 알 수 있다.

그럼 범위를 둘로 나누어서 양수, 음수 각각 절댓값을 인덱스로 하는 배열 두 개를 쓰면 안되나? 싶을 수도 있겠지만 노트북으로 실행해봤을 때 OutOfMemoryError가 발생한다. 물론 JVM 옵션을 이래저래 만져서 최대로 할당할 수 있는 메모리의 상한을 올려주는 식으로 가능할지도 모르겠지만,, 좋은 방법은 아닌 것 같다.

왜냐? 문제에서 주어지는 정수의 개수는 100,000개인데 이 수들이 있는지 없는지 확인하기 위해 2^32개 중 최대 100,000개(모든 수가 다른 경우)를 쓴다고 해도 99.999997... 퍼센트의 공간을 낭비하는, 희소 행렬쯤 되는 성긴 배열이기 때문이다. 이럴 바에는 충돌을 감수하더라도 Set을 써주는 쪽이 차라리 합리적일 것이다.

접근 2 : 이분 탐색

물론 Set으로도 풀리지만, 이분 탐색을 써서 풀 수도 있다. 개인적인 소감이지만 문제 풀 때 Set보단 Binary Search가 필요할 때가 훨씬 많았던 것 같다.

이걸 찾아 보고 있을 정도라면 이분 탐색이 뭔지 정도는 구경해봤을 것 같아 자세한 설명은 따로 안한다. 혹시 가물가물하다면 바킹독님의 알고리즘 강의 중 이분 탐색 파트를 들어보면 좋을 것 같다. 이 분 진짜 설명 잘 해주신다.

내가 이해한 바로는 이렇다. 정렬된 배열에 대해, 특정 구간의 양 끝인 [low, high]를 기준으로 정중앙 mid에 놓인 값이 내가 찾으려던 그 값일 때까지 탐색을 계속한다. 하지만 아니라면?

  1. 만약 그 값이 내가 찾으려던 값보다 작다면, 그보다 작거나 같은 왼쪽은 더 볼 필요가 없다. 따라서 [mid+1, high] 구간에서 다시 정중앙 값을 확인한다.
  2. 만약 그 값이 내가 찾으려던 값보다 크다면, 그보다 크거나 같은 오른쪽은 더 볼 필요가 없다. 따라서 [low, mid-1] 구간에서 다시 정중앙 값을 확인한다.

결과를 찾지 못할 때마다 탐색 범위를 반씩 잘라내기에 이분 탐색이라고 부르는데, 어떤 수가 배열에 존재하는지 확인하는 알고리즘의 시간 복잡도는 O(정렬_시간복잡도+logN)이다. 컴퓨터 과학 분야에서 로그의 밑을 따로 표현하지 않는다면 일반적으로 밑이 2인 로그인데, 찾는 수를 low == high가 될 때까지 찾아야 하는 최악의 경우를 따져 시간 복잡도를 구해보자.

  1. 배열의 크기가 N일 때, 첫 탐색에서 찾지 못했다면 탐색 범위는 N/2가 된다.
  2. 두 번째 탐색에서 찾지 못했다면 탐색 범위는 N/2^2가 된다.
  3. 세 번째 탐색에서 찾지 못했다면 탐색 범위는 N/2^3이 된다.
  4. k번째 탐색에서 찾지 못했다면 탐색 범위는 N/2^k가 된다.
  5. 이 k번째 탐색에서 low == high가 되었다면, 범위의 크기가 1이 되었다는 의미이다.
  6. 따라서 N/2^k ≈ 1이므로, 양 변에 2^k를 곱해 N ≈ 2^k와 같이 표현할 수 있다.
  7. 여기서 양 변에 밑을 2로 하는 로그를 취해주면 K ≈ logN이 된다.
  8. 여기서!! K가 최악의 경우 탐색해야 하는 횟수라 했으므로, Big O 표기법으로 O(logN)으로 표현할 수 있는 것이다.

그런데 만약 배열 안에 내가 찾는 수가 없다면 어떨까? 밑도 끝도 없이 어떤 수를 찾기 위해 low와 high를 갱신하기만 한다면 탐색이 끝나질 않을 것이다. 나는 이 부분이 항상 헷갈렸었는데 결론부터 말하자면 while (low <= high)를 탐색 루프로 사용한다.

왜냐! 아래와 같은 배열에서 40을 찾는다고 생각해보자.

Index012345
Number102030405060
  1. 탐색 범위 [0, 5], mid=(0+5)/2=2, arr[2] = 30, 찾으려는 40보다 작으므로 왼쪽 절반 버림
  2. 탐색 범위 [3, 5], mid=(3+5)/2=4, arr[4] = 50, 찾으려는 40보다 크므로 오른쪽 절반 버림
  3. 탐색 범위 [3, 3]...

여기서 만약 while (low < high)였으면 3번째 탐색은 일어날 수 없으므로 배열 안에 40이 없다는 결론이 날 것이다. 문제 풀 때 헷갈리면 직접 써보면 된다!

구현 2-1 : ArrayList 구현

몇 단계에 걸쳐 코드를 고쳐볼건데, 일단 제일 먼저 List 인터페이스를 가지는 ArrayList를 써봤다.

static boolean isExistIn(List<Integer> numbers, int targetNum) {
    int low = 0;
    int high = numbers.size() - 1;

    // low와 high가 엇갈려서 순서를 유지하며 mid를 찾을 수 없게 되면 탐색 종료
    while (low <= high) {
        // low, mid, high의 순서로 low와 high 중앙의 위치
        int mid = (low + high) >> 1;
        // 대조해볼 값
        int candidate = numbers.get(mid);

        // 찾으려는 값보다 작다면, 그보다 작거나 같은 왼쪽은 볼 필요가 없음
        if (candidate < targetNum) {
            low = mid + 1;
        }
        // 찾으려는 값보다 크다면, 그보다 크거나 같은 오른쪽은 볼 필요가 없음
        else if (candidate > targetNum) {
            high = mid - 1;
        }
        // 값을 찾았으면 찾았음을 알리며 탐색 종료
        else {
            return true;
        }
    }

    return false;
}

다른쪽은 크게 볼게 없어서 이분 탐색 부분만 찾아왔다(물론 이분 탐색을 수행해야 하므로 numbers는 정렬되어 있는 상태!).

Arrays.sort vs Collections.sort

Array가 아니라 numbers를 쓴 건, 오늘 SSAFY 알고리즘 단톡에서 배열에 대한 정렬인 Arrays.sort와 리스트에 대한 정렬인 Collections.sort의 성능 차이가 있을 수 있다는 말을 들어서 그랬다. (정렬 알고리즘에 대한 설명을 하는건 주제에 너무 벗어나므로, stable 등의 측면은 다른 포스트에서 다루겠다!)

뭔 말인가 싶어서 찾아봤는데, 우선 Arrays.sort가 int 같은 Primitive 타입을 요소로 하는 정렬을 수행할 때는 Dual pivot quick sort라는 알고리즘을 사용한다고 한다. 말 그대로 pivot을 두 개 사용하기 때문에 Quick sort와 달리 구간을 3개로 나누므로 밑이 2에서 3으로 증가, 더 효율적인 시간 복잡도를 기대할 수 있다. 하지만 Quick sort 자체가 가지는 한계, 즉 pivot을 잘못 선택하는 경우 발생할 수 있는 최악의 시간 복잡도인 O(N^2)은 피할 수가 없다고 한다.

반면 Arrays.sort에 Reference 타입을 요소로 하는 정렬이 수행될 때는 Tim sort를 사용한다. 삽입 정렬과 병합 정렬을 적절히 활용한 똑똑한 알고리즘인데, 최적의 경우 O(N), 평균과 최악의 경우 둘 다 O(NlogN)의 시간 복잡도가 보장된다.

Collections.sort의 경우,, 내가 이해한대로라면 List의 제네릭 타입으로 reference type이 들어가는데, 내부에서 어차피 Tim sort를 수행하기 때문에 항상 최악의 경우에도 O(NlogN)의 시간 복잡도가 보장된다는 것 같다.

더 찾아보면 자료 구조의 특성에 따른 캐시의 특성처럼 뭔가 심연이 비치는 것 같은데 이런 부분까지 저격해서 내면 지금으로선 틀릴 것 같다 ㅎ 기억해두고 있다가 도저히 안 될 때 한 번 시도해볼 것 같아서,, 언젠가 다룰 Dual pivot quick sort, Tim sort 포스트에서 자세히 살펴보련다.

아 그래도 Arrays.sort를 써서 한 번 비교해볼까?

static boolean isExistIn(int[] numbers, int targetNum) {
    int low = 0;
    int high = numbers.length - 1;

    // low와 high가 엇갈려서 순서를 유지하며 mid를 찾을 수 없게 되면 탐색 종료
    while (low <= high) {
        // low, mid, high의 순서로 low와 high 중앙의 위치
        int mid = (low + high) >> 1;
        // 대조해볼 값
        int candidate = numbers[mid];

        // 찾으려는 값보다 작다면, 그보다 작거나 같은 왼쪽은 볼 필요가 없음
        if (candidate < targetNum) {
            low = mid + 1;
        }
        // 찾으려는 값보다 크다면, 그보다 크거나 같은 오른쪽은 볼 필요가 없음
        else if (candidate > targetNum) {
            high = mid - 1;
        }
        // 값을 찾았으면 찾았음을 알리며 탐색 종료
        else {
            return true;
        }
    }

    return false;
}

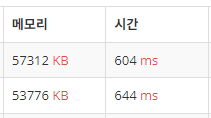
위의 풀이가 Arrays.sort, 아래 풀이가 Collections.sort인데 극적인 차이는 없는 것 같다. 다행,,

구현 2-2 : 내장 함수 활용 구현

사실 직접 구현할 필요는 없고, 배열과 리스트 모두 .binarySearch라는 메서드가 각각 지원된다. 마지막 구현이었던 배열을 기준으로 적용해보면 아래와 같다.

static boolean isExistIn(int[] numbers, int targetNum) {
    int targetIdx = Arrays.binarySearch(numbers, targetNum);
    return targetIdx >= 0;
}

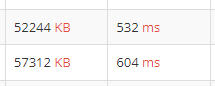
위의 제출이 위의 코드인데,, 쓸 수 있다면 내장 함수를 쓰는 쪽이 이로울 것 같다.

여하튼 결과가 좀 이상한데, 존재 여부가 아니라 배열 안에서 targetNum의 위치를 찾아준다. 하긴 위치를 특정할 수 있다는 건 배열 안에 무조건 있다는 뜻이니까 범용성을 생각하면 위치를 반환해주는 쪽이 나을 것 같기는 하다.

그럼 배열에 없을 땐? 흔히 하는 구현처럼 -1을 반환할까? 아니다. 문서를 보자.

뭔가 장황한데 배열 안에 원하는 값이 없다면 (-(insertion point) - 1)을 반환한다고 한다. 이게 뭔지 이해하려면 이따 낮에 쓸 upper bound과 lower bound에 대해 먼저 배우는게 좋을 것 같다.

마무리

여기까진 얼추 자료 안보고도 할 수 있는 쉬운 부분이라 빠르게 살펴볼 수 있었다.

시간이 너무 늦기도 해서,, 다음 부분인 upper&lower bound는 낮에 써봐야겠다. 빠세!

참고한 자료

profile
급식
뭐 먹고 살지.
이전 포스트

BOJ 6198. 옥상 정원 꾸미기 (G5)

다음 포스트

이분 탐색 박살내기 2 : BOJ 10816 숫자 카드 2 (S4)

1개의 댓글

comment-user-thumbnail
JohnSik
약 2시간 전

혹시 보신곳이 하이퍼센트 인가요

답글 달기