Texture Synthesis by Non-parametric Sampling

A. A. Efros and T. K. Leung, "Texture Synthesis by Non-parametric Sampling" 논문을 요약, 정리해보는 시간을 갖겠습니다.

Abstract

Texture synthesis는 초기의 기준점(seed)을 이용해 한번에 한 픽셀씩 합성(생성)시켜 새로운 이미지를 만들어내는 것을 의미합니다.

논문에서는 마르코프 랜덤 필드(MRF)를 이용하고, synthesize할 픽셀의 주변 값들과 유사한 이미지 패치를 샘플 이미지에서 모두 찾아 픽셀의 조건부 분포(conditional distribution)를 추정합니다.

무작위 정도(만들어지는 이미지의 무작위 정도; 규칙적인 texture로 이루어져 있는가 아닌가)는 인간의 인지능력에 직관적인 파라미터 하나만을 이용해 조절합니다.

논문에서는 Non-parametric method를 제안하며, 이 method는 이미지의 local structure을 최대한 보존하고 다양한 종류의 synthesis와 real-world에서도 좋은 결과를 내는 것에 집중했습니다.

Introduction

Texture synthesis 문제는 다음과 같이 정형화할 수 있습니다.

무한한 2D 평면에 어떤 크기, 정적 분포(stationary distribution)를 띄고 있는 한 texture가 있다고 가정한다. 유한한 sample들이 주어졌을 때, 그 sample을 이용해 동일한 texture의 다른 sample들을 synthesize 문제이다.

추가적인 조건이 없다면, 이 문제는 ill-posed 문제가 됩니다. sample이 무한한 2D 평면의 어떤 texture에서 왔는지 알 수가 없기 때문입니다.

보통 texture의 특성과 texture elements의 크기, 이 둘을 알 만큼 충분한 크기의 sample image를 추가적인 조건으로 사용합니다.

texture는 2가지로 분류됩니다

Regular : texture elements의 반복으로 이루어진 texture
Stochastic : 명확한 texture elements 없이 뭔가 무작위적인 texture

하지만 real-world에 존재하는 texture는 정확히 한쪽으로 분류되지 않습니다.

논문에서는 이미지의 공간적인 locality를 기반으로 한 non-parametric model을 제시하고 hole-filling과 같은 texture synthesis에서 좋은 효과를 보이는 알고리즘을 제시합니다.

Previous work

Texture synthesis에 관한 선행연구들을 말하고 있습니다. Probability distribution을 이용한 방법들 등 여러가지 선행연구에 관해 간단하게 설명하고 있습니다.

Our Approach

여러 선행연구를 고려해 3가지의 주요 challenge를 얻을 수 있습니다.

1. synthesize 할 unit과 unit의 context를 어떻게 정의할 것 인지
2. Probability distribution을 어떻게 구축할 것 인지
3. 2D에서의 synthesis 과정을 어떻게 선형화시킬 것 인지

논문에서 제시하는 알고리즘은 첫 seed에서 시작해서 픽셀 단위로 확장시키는 형태입니다.

임의의 픽셀 p를 synthesize 할 unit으로, p를 중심점으로 하는 길이 w의 square window( square image patch)를 context로 선정합니다.

synthesis를 수행하기 위해서는, 픽셀 p의 모든 경우의 수에 관한 확률 분포표가 필요합니다. 알고리즘에서는 픽셀 p가 가질 수 있는 모든 값에 대한 히스토그램을 이용해 p의 분포를 얻습니다.
아래 그림은 알고리즘을 표현한 그림입니다.

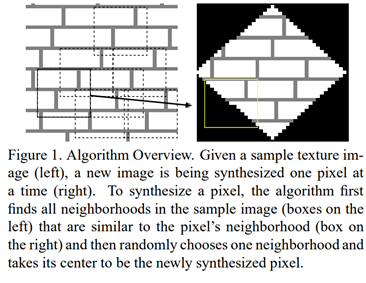
The Algorithm

논문에서는 texture를 MRF(Markov random field)로 모델링합니다.

즉, 한 픽셀에 대해 이웃의 밝기값이 주어져있다고 가정했을 때 픽셀의 밝기값에 대한 확률 분포는 전체에서 픽셀과 그 이웃을 제외한 나머지의 영향을 받지 않는다(독립적이다)는 말입니다.

여기서 이웃은 위에서 언급한 것처럼 unit 픽셀을 중심으로 한 square window를 칭합니다. 이 window의 크기는 free parameter 인데, user가 생각하기에 생성될 texture가 얼마나 stochastic 한지에 따라 정해집니다.

위의 이미지는 window의 크기에 따른 synthesize 결과차이 입니다.

Synthesizing one pixel

$I$ = 합성으로 만들 이미지
$I_s$$_m$$_p$ = 샘플이미지
$I_r$$_e$$_a$$_l$ = real infinite texture
$p$ = synthesize 대상 픽셀
$w(p)$ = p를 중심으로 하는 square window(image patch)
$d(w_1, w_2)$ = 두 개의 image patch 사이의 perceptual distance

우선 $I$ 에서 $p$ 를 제외한 모든 픽셀 값을 알고있다고 가정한 뒤, $p$ 값을 synthesize 하기 위해 조건부 확률 분포 $P(p|w(p))$에 대한 근사치를 구축하고 그 분포에서 sampling 하면 됩니다.

다음과 같은 수식을 하나 정의할 수 있습니다.

$\Omega(p)$ = $\{$$w'$ $\subset$ $I_r$$_e$$_a$$_l$ : $d(w', w(p)) = 0\}$

이는 $I_r$$_e$$_a$$_l$ 에 존재하는 $w'$ $(w(p)$와 차이가 없는 image patch)) 의 집합이고, 이를 이용해 $p$ 의 조건부 확률 분포를 추정할 수 있습니다($w'$ 에서 중심 픽셀이 어떤 값을 가지는지를 통해).

하지만 우리에겐 $I_r$$_e$$_a$$_l$ 이 아닌 $I_s$$_m$$_p$가 주어져 있으므로 $\Omega(p)$를 대체할 수 있는 $\Omega'(p)$ 를 찾아야 합니다.
$\Omega'(p)$ 를 찾는 과정은 다음과 같습니다.

1. $w_b$ = $argmin_w$ $d(w(p), w)$ $\subset$ $I_s$$_m$$_p$
2. $\Omega'(p)$ = $\{$$w$ $\subset$ $I_s$$_m$$_p$ : $d(w, w(p))$ $<$ (1+$\epsilon$)$d(w(p), w_b)$$\}$

논문에서는 $\epsilon$을 0.1로 설정했습니다.
따라서 $w$의 집합 $\Omega'(p)$ 에 의해 $p$ 의 조건부 확률 분포를 추정할 수 있습니다.

distance 함수

perceptual distance인 $d$ 함수는 normalized sum of squaerd differences를 사용하는데 이미지의 local structure를 보존하기 위해 2차원 Gaussian kernel을 곱해주는 형태로 정의됩니다(image patch 중심부의 error를 더 부각시키기 위함).

따라서 $d$ 함수의 최종형태는 아래와 같습니다.

$d$ = $d_S$$_S$$_D$ $*$ $G$

Synthesizing texture

이전 단계에서는 주위 픽셀값들을 전부 알고 있다는 가정하에 한 픽셀을 synthesize 하는 방법에 대해 논의했습니다.

하지만 실질적으로 synthesize를 해야 할 이미지에서는 한 픽셀만 비어있고 나머지 값은 다 알고있는 경우는 없습니다.

즉 $p$ 를 synthesize 해야하는데, $w(p)$의 값 중 일부만 알고있는 경우입니다. 따라서 $p$의 조건부 확률 분포를 구하는 알고리즘을 조건에 맞춰 수정해야합니다.

수정된 알고리즘은 다음과 같습니다.

1. $w(p)$에서 알고있는 픽셀값들만 비교를 한다.
2. 비교를 통해 발생된 error(distance)를 값을 알고있는 픽셀들의 개수로 normalize 한다.
3. normalize된 error를 이용해 이전 알고리즘과 같이 $p$ 의 확률 분포를 구한다.

이때 구한 $p$의 확률 분포가 $w(p)$의 값이 어느정도 채워졌을 때에도 유효한지에 대한 의문이 생기는데, 논문에서는 좋은 근사치를 보여줬다고 말합니다.

Results

알고리즘은 다양한 texture에서 좋은 성능을 보였습니다.


첫번째 이미지는 real-world texture, 두번째 이미지는 contrained texture(ex:hole filling synthesis) 에 대한 synthesis 결과를 보여줍니다.

또한 선행연구( J. S. D. Bonet. "Multiresolution sampling procedure for analysis and synthesis of texture images")와 synthesis 결과를 비교해봐도 좋은 모습을 확인할 수 있었습니다.

Limitations and Future Work

이 알고리즘의 문제점은 어떤 texture 에서는 가끔 잘못된 픽셀 값을 찾아서 수행되거나 혹은 한 context에만 갇혀서 의미없는 복사-붙여넣기가 수행되는 경우가 있습니다.

이런 문제점들은 texture가 너무 다른 type의 elements로 이루어져 있거나 혹은 같은 elements 지만 조명에 의해서 다르게 보이는 경우에 square window와 비슷한 context를 sample 이미지에서 찾기 어려워져 생깁니다.

아래는 이런 문제가 일어난 결과 이미지입니다.

이런 문제들은 sample 이미지가 크면 클수록 생기지 않습니다.

논문에서는 window size를 automatic으로 설정하는 법, window의 모양을 다양하게 설정해보는 법(정사각형을 제외한)과 같은 다양한 후속연구를 진행하고 있음을 알립니다.

Applications

이 알고리즘은 synthesize 할 region의 모양이나 혹은 sampling 할 region의 모양에 구애를 받기 때문에(pixel 단위로 수행하기 때문) 많은 곳에 이용될 수 있습니다.

또한 이미지의 local structure(ex : 직선의 유지 등) 도 고려되었기 때문에 synthesized image에서 시각적으로 어색하지 않습니다.

이 밖에도 많은 분야(motion synthesis 등)에서 사용될 수 있음을 말하며 논문이 마쳐집니다.

참고자료

A. A. Efros and T. K. Leung, “Texture synthesis by non-parametric
sampling,” in Proceedings of the seventh IEEE international conference
on computer vision, vol. 2. IEEE, 1999, pp. 1033–1038.

마르코프 랜덤 필드의 성질 - http://cv.jbnu.ac.kr/index.php?mid=ml