distortion correction(3)

전통적인 왜곡 보정 방법에 관한 논문 두 가지를 간략하게 리뷰해보는 시간을 갖겠습니다.

비대칭 왜곡 어안렌즈를 위한 영상 손실 최소화 왜곡 보정 기법

이 논문에서는 왜곡 보정을 위해 왜곡 모델이 포함된 카메라 모델을 설정하고 캘리브레이션 과정을 통해 카메라 파라미터를 구해 왜곡이 보정된 이미지를 생성하는 과정을 이용했음.

왜곡 모델이 포함된 카메라 모델

왜곡렌즈로 만들어진 이미지의 경우 수평 화각이 수직 화각에 비해 크게 설계 되어 있음.

이로 인해 캘리브레이션 전에 두 화각을 일치시킬 필요가 있음.

따라서 이 화각을 일치시킬 계수를 구하여 이미지의 장축과 단축을 일치시켜줌.

$S_{pre\_x}$ = $E_x/E_y$

이때 $S_{pre\_x}$는 일치시킬 계수(스케일링 인자)이며 $E_x$, $E_y$는 이미지의 장단축 비율을 나타냄.

이 계수를 이미지의 특징점에 곱하여 이미지의 장단축을 일치시켜줌.

또한 이미지에서 추출한 특징점을 이용해 카메라 파라미터 값을 추정하고, 이 추정한 값을 이용해 카메라 모델을 생성함.

생성한 카메라 모델에 대해 왜곡을 가하는데 이때 사용되는 왜곡 함수는

$r_d = (1/w) arctan(2r_u* tan(w/2))$

함수가 사용되고 이때 $r_u$ 는 왜곡이 없을 때의 영상 중심으로부터 거리, $r_d$는 왜곡되었을 때의 영상 중심으로부터 거리를 의미함.

캘리브레이션 이원화

앞서 말한 카메라 캘리브레이션 과정 중 캘리브레이션이 수행될 때 내외부 파라미터를 계속적으로 동시에 구하면 연산속도가 느린 단점이 있음.

이를 개선하기 위해 캘리브레이션 과정을 내부 파라미터를 구하는 과정과, 외부 파라미터를 구하는 과정으로 나누었음.

카메라 내부 파라미터를 먼저 계산하고, 다른 위치와 각도에서 얻은 이미지에 대해 캘리브레이션을 수행할 때 앞서 구한 내부 파라미터를 입력값으로 사용하면 지속적으로 내외부 파라미터를 구할 필요가 없고 외부 파라미터만 구하면 되며, 연산속도에서 이점이 생김.

왜곡 보정 이미지 생성

왜곡 보정을 위해 왜곡 이미지 좌표에서 앞서 말한 왜곡 함수의 역함수를 이용해 왜곡 보정을 진행하면 보정 이미지에 공백 픽셀이 발생하게 됨.

이를 막기 위해 보정된 이미지가 있다고 가정하여 보정된 이미지의 좌표를 앞서 구한 왜곡 함수에 적용해 왜곡 이미지 좌표를 구하고, 해당 좌표의 픽셀값을 보정된 이미지의 좌표에 적용함.

시야각 손실을 줄이기 위한 방법

왜곡 보정후 영상의 크기가 ($U_x, U_y$)라고 가정하면, 보정된 영상 좌표에 대하여 해당 좌표 위치에 대한 비율을 구할 수 있음.

$U_{ratio}$ = $\sqrt{X_u^2 + Y_u^2} / \sqrt{(U_x/2)^2 + (U_y/2)^2}$

이 비율을 이용해 중심점에서 먼 좌표는 보정 비율을 작게, 중심점에서 가까운 좌표는 보정 비율을 크게 하여 시야각에 대한 손실을 줄일 수 있음.

FOV 모델과 2D 패턴을 이용한 왜곡 중심 추정 기법

이 논문에서는 이전까지의 왜곡 보정 기법은 왜곡 중심에 대한 추정이 없었기 때문에 왜곡 보정의 정확도가 떨어질 수 있음을 지적하며 왜곡 중심을 추정하고 이에 알맞게 왜곡 보정을 진행하는 방법을 제시.

보정 순서는 다음과 같음.

1. FOV 모델을 이용해 왜곡 계수 추정

2. 추정된 왜곡 계수와 직선 불변 법칙을 이용해 왜곡 중심점 추정

3. 추정된 왜곡 계수와 중심점을 이용해 왜곡 이미지 보정

왜곡 계수 추정

FOV 모델의 경우 앞서 리뷰한 논문에서 등장한 왜곡 함수

$r_d = (1/w) arctan(2r_u* tan(w/2))$

를 사용.

왜곡 이미지 모든 픽셀에 대해 앞서 언급한 함수의 역함수를 적용해 왜곡 계수를 각각 추정하며 이때 모든 픽셀에 대해 오차가 최소가 되는 왜곡 계수를 추정함.

왜곡 중심점 추정

왜곡 중심점을 추정하기 위해서 2D 패턴(체커보드 패턴)을 이용함.

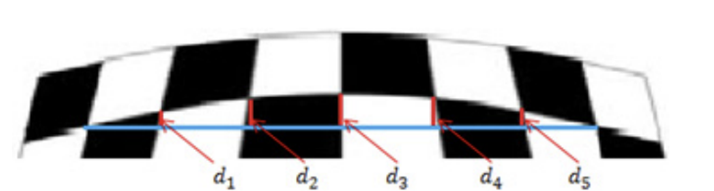
그림과 같이 해당 체커보드에 대하여 직선의 왜곡 오차($d_n$)를 구함.

이 직선의 왜곡 오차가 최소화 되는 구간을 찾아 해당 구간에서 왜곡 중심을 구함.

마무리

오늘은 전통적인 왜곡 보정에 관한 논문 두 가지를 리뷰했습니다.

다음 포스팅에서 뵙겠습니다.

감사합니다.