문제 설명

건설회사의 설계사인 죠르디는 고객사로부터 자동차 경주로 건설에 필요한 견적을 의뢰받았습니다.
제공된 경주로 설계 도면에 따르면 경주로 부지는 N x N 크기의 정사각형 격자 형태이며 각 격자는 1 x 1 크기입니다.
설계 도면에는 각 격자의 칸은 0 또는 1 로 채워져 있으며, 0은 칸이 비어 있음을 1은 해당 칸이 벽으로 채워져 있음을 나타냅니다.
경주로의 출발점은 (0, 0) 칸(좌측 상단)이며, 도착점은 (N-1, N-1) 칸(우측 하단)입니다. 죠르디는 출발점인 (0, 0) 칸에서 출발한 자동차가 도착점인 (N-1, N-1) 칸까지 무사히 도달할 수 있게 중간에 끊기지 않도록 경주로를 건설해야 합니다.
경주로는 상, 하, 좌, 우로 인접한 두 빈 칸을 연결하여 건설할 수 있으며, 벽이 있는 칸에는 경주로를 건설할 수 없습니다.
이때, 인접한 두 빈 칸을 상하 또는 좌우로 연결한 경주로를 직선 도로 라고 합니다.
또한 두 직선 도로가 서로 직각으로 만나는 지점을 코너 라고 부릅니다.
건설 비용을 계산해 보니 직선 도로 하나를 만들 때는 100원이 소요되며, 코너를 하나 만들 때는 500원이 추가로 듭니다.
죠르디는 견적서 작성을 위해 경주로를 건설하는 데 필요한 최소 비용을 계산해야 합니다.
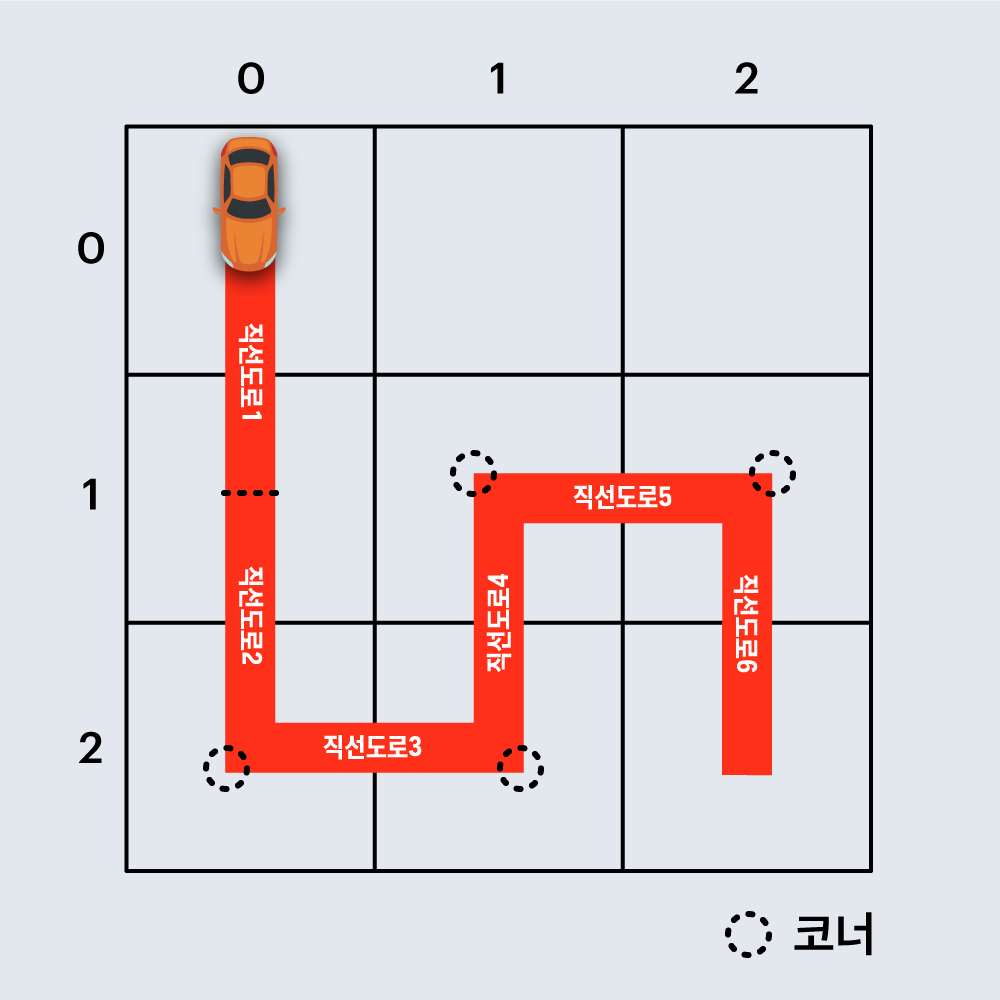
예를 들어, 아래 그림은 직선 도로 6개와 코너 4개로 구성된 임의의 경주로 예시이며, 건설 비용은 6 x 100 + 4 x 500 = 2600원 입니다.
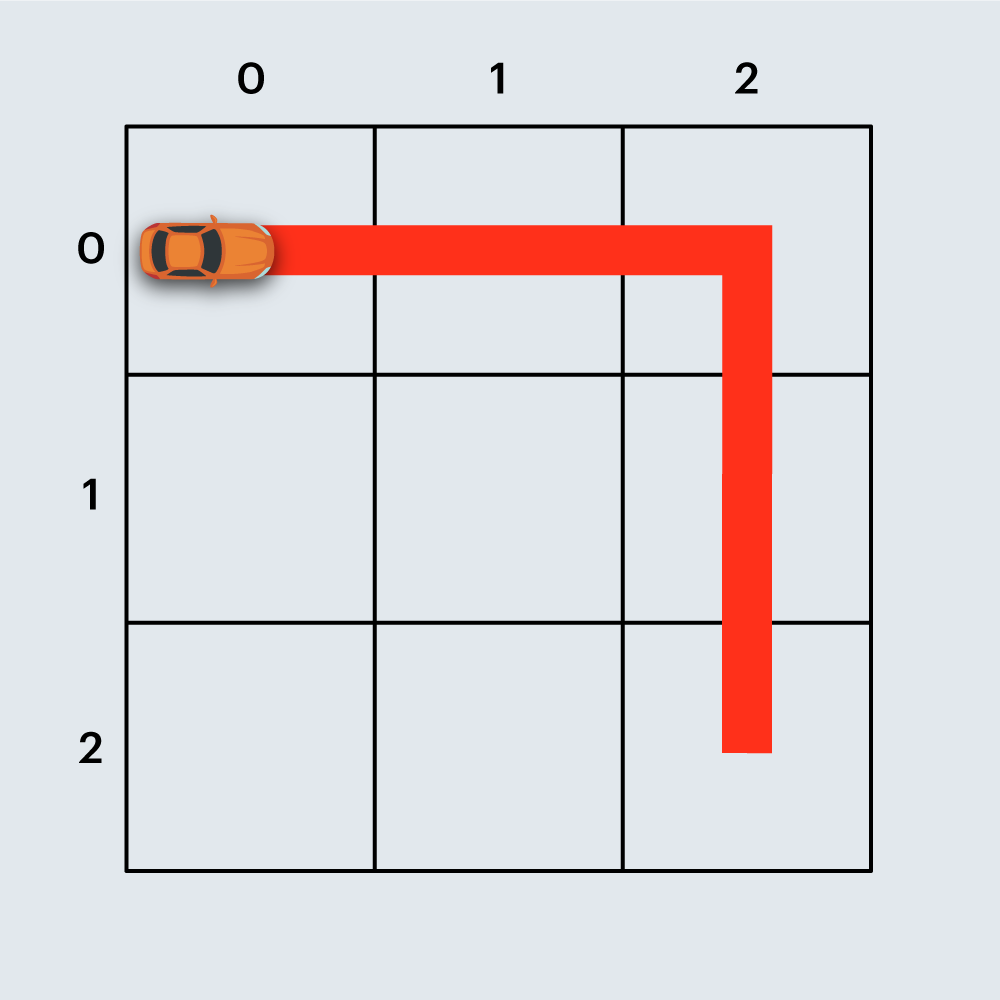
또 다른 예로, 아래 그림은 직선 도로 4개와 코너 1개로 구성된 경주로이며, 건설 비용은 4 x 100 + 1 x 500 = 900원 입니다.
도면의 상태(0은 비어 있음, 1은 벽)을 나타내는 2차원 배열 board가 매개변수로 주어질 때, 경주로를 건설하는데 필요한 최소 비용을 return 하도록 solution 함수를 완성해주세요.
[제한사항]
- board는 2차원 정사각 배열로 배열의 크기는 3 이상 25 이하입니다.
- board 배열의 각 원소의 값은 0 또는 1 입니다.
- 도면의 가장 왼쪽 상단 좌표는 (0, 0)이며, 가장 우측 하단 좌표는 (N-1, N-1) 입니다.
- 원소의 값 0은 칸이 비어 있어 도로 연결이 가능함을 1은 칸이 벽으로 채워져 있어 도로 연결이 불가능함을 나타냅니다.
- board는 항상 출발점에서 도착점까지 경주로를 건설할 수 있는 형태로 주어집니다.
- 출발점과 도착점 칸의 원소의 값은 항상 0으로 주어집니다.
입출력 예
| board | result |
|---|---|
| [[0,0,0],[0,0,0],[0,0,0]] | 900 |
| [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]] | 3800 |
| [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]] | 2100 |
| [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]] | 3200 |
풀이
다익스트라로 풀 수 있는 쉬운 문제였다.
다만, 내가 간과한 점이 이 문제에서는 시작할 수 있는 경우의 수가 2개가 존재하는데 (오른쪽으로 출발하는 경우, 아래쪽으로 출발하는 경우) 이 것을 하나의 큐에 넣고 다익스트라로 구했더니 몇 개의 테스트 케이스에서 오답이 발생했다.
최단 거리를 갱신할 때, 최소값과 같은 경우도 큐에 넣어줬는데 틀리더라..
거리값 계산은 (횡 → 횡), (종 → 종) 은 +100, 직선도로만 건설하면 되므로, (횡 → 종), (종 → 횡) 은 +600, 코너와 직선도로를 함께 건설해야 한다.
그래서 풀이를 찾아보니까, 두 번의 BFS로 나눠서 답을 구하는 것 같았다.
다음에 유사한 문제가 나온다면, 꼭 ! 꼭 ! 맞춰야지.
코드
from collections import deque
N = 0
def get_cost(d1, d2, cost):
if (d1 == 'R' or d1 == 'L') and (d2 == 'L' or d2 == 'R'):
return cost + 100
elif (d1 == 'D' or d1 == 'U') and (d2 == 'D' or d2 == 'U'):
return cost + 100
elif (d1 == 'R' or d1 == 'L') and (d2 == 'D' or d2 == 'U'):
return cost + 600
elif (d1 == 'U' or d1 == 'D') and (d2 == 'L' or d2 == 'R'):
return cost + 600
def bfs(x, y, cost, direct, answer, board):
global N
q = deque([(x, y, cost, direct)])
check = [[0 for _ in range(N)] for _ in range(N)]
check[y][x] = 1
while q:
x, y, cost, cur_dir = q.popleft()
if x == N - 1 and y == N - 1:
answer.append(cost)
continue
for dy, dx, new_dir in (0, 1, 'R'), (1, 0, 'D'), (0, -1, 'L'), (-1, 0, 'U'):
ny, nx = y + dy, x + dx
if (0 <= ny < N and 0 <= nx < N) and not board[ny][nx]:
new_cost = get_cost(cur_dir, new_dir, cost)
if not check[ny][nx] or new_cost < check[ny][nx]:
check[ny][nx] = new_cost
q.append((nx, ny, new_cost, new_dir))
def solution(board):
global N
answer = []
N = len(board)
bfs(0, 0, 0, 'R', answer, board)
bfs(0, 0, 0, 'D', answer, board)
print(answer)
return min(answer)