[ 카카오 / Python ] 2023 KAKAO BLIND RECRUITMENT - 1, 2, 3 떨어트리기

문제 설명

춘식이는 트리의 1번 노드에 숫자 1, 2, 3 중 하나씩을 계속해서 떨어트려 트리의 리프 노드1에 숫자를 쌓는 게임을 하려고 합니다.
아래 그림은 게임의 예시를 나타냅니다.

트리의 모든 간선은 부모 노드가 자식 노드를 가리키는 단방향 간선입니다.
모든 부모 노드는 자식 노드와 연결된 간선 중 하나를 길로 설정합니다.
실선 화살표는 길인 간선입니다.
점선 화살표는 길이 아닌 간선입니다.
모든 부모 노드는 자신의 자식 노드 중 가장 번호가 작은 노드를 가리키는 간선을 초기 길로 설정합니다.
[게임의 규칙]은 아래와 같습니다.

1. 1번 노드(루트 노드)에 숫자 1, 2, 3 중 하나를 떨어트립니다.
   2.숫자는 길인 간선을 따라 리프 노드까지 떨어집니다.
2. 숫자가 리프 노드에 도착하면, 숫자가 지나간 각 노드는 현재 길로 연결된 자식 노드 다음으로 번호가 큰 자식 노드를 가리키는 간선을 새로운 길로 설정하고 기존의 길은 끊습니다.
   • 만약 현재 길로 연결된 노드의 번호가 가장 크면, 번호가 가장 작은 노드를 가리키는 간선을 길로 설정합니다.
   • 노드의 간선이 하나라면 계속 하나의 간선을 길로 설정합니다.
3. 원하는 만큼 계속해서 루트 노드에 숫자를 떨어트릴 수 있습니다.
   • 단, 앞서 떨어트린 숫자가 리프 노드까지 떨어진 후에 새로운 숫자를 떨어트려야 합니다.

[게임의 목표]는 각각의 리프 노드에 쌓인 숫자의 합을 target에서 가리키는 값과 같게 만드는 것입니다.
예를 들어, target이 [0, 0, 0, 3, 0, 0, 5, 1, 2, 3]일 경우 아래 표와 같은 의미를 가집니다.

노드 번호	노드에 쌓인 숫자의 합
1	0
2	0
3	0
4	3
5	0
6	0
7	5
8	1
9	2
10	3

target대로 리프 노드에 쌓인 숫자의 합을 맞추기 위해서는 [2, 1, 2, 2, 1, 3, 3]순으로 숫자를 떨어트리면 됩니다.

아래 두 그림은 순서대로 1, 2번째 숫자 [2, 1]을 떨어트린 뒤의 길 상황을 나타냅니다.

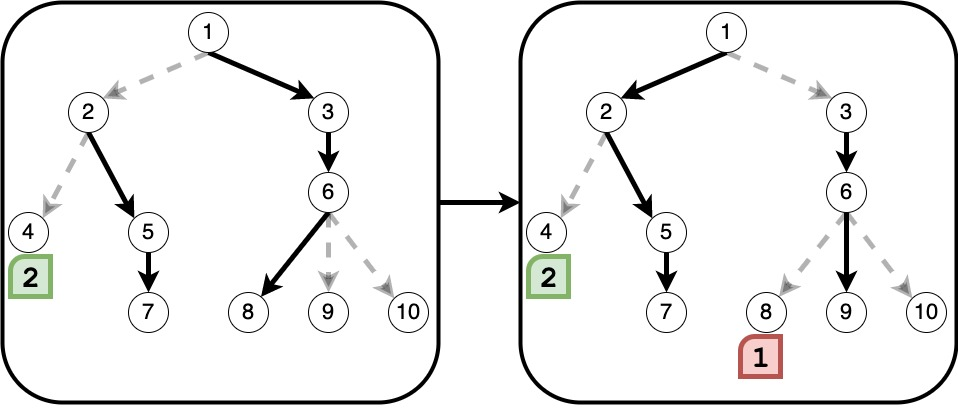
• 숫자 2는 떨어지면서 1번 노드와 2번 노드를 지나갔습니다.
  • 1번 노드는 3번 노드를 가리키는 간선을 길로 설정합니다.
  • 2번 노드는 5번 노드를 가리키는 간선을 길로 설정합니다.
• 숫자 1은 떨어지면서 1번 노드, 3번 노드, 6번 노드를 지나갔습니다.
  • 1번 노드는 3번 노드보다 번호가 큰 노드를 가리키는 간선이 없으므로 다시 2번 노드를 가리키는 간선을 길로 설정합니다.
  • 3번 노드는 간선이 하나이므로 계속해서 6번 노드를 가리키는 간선을 길로 설정합니다.
  • 6번 노드는 9번 노드를 가리키는 간선을 길로 설정합니다.

아래 두 그림은 순서대로 3, 4번째 숫자 [2, 2]를 떨어트린 뒤의 길 상황을 나타냅니다.

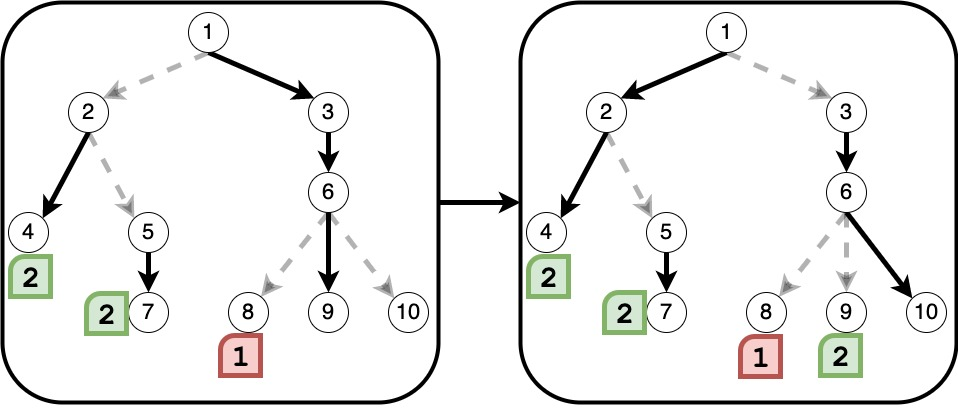
아래 세 그림은 순서대로 5, 6, 7번째 숫자 [1, 3, 3]을 떨어트린 뒤의 길 상황을 나타냅니다.

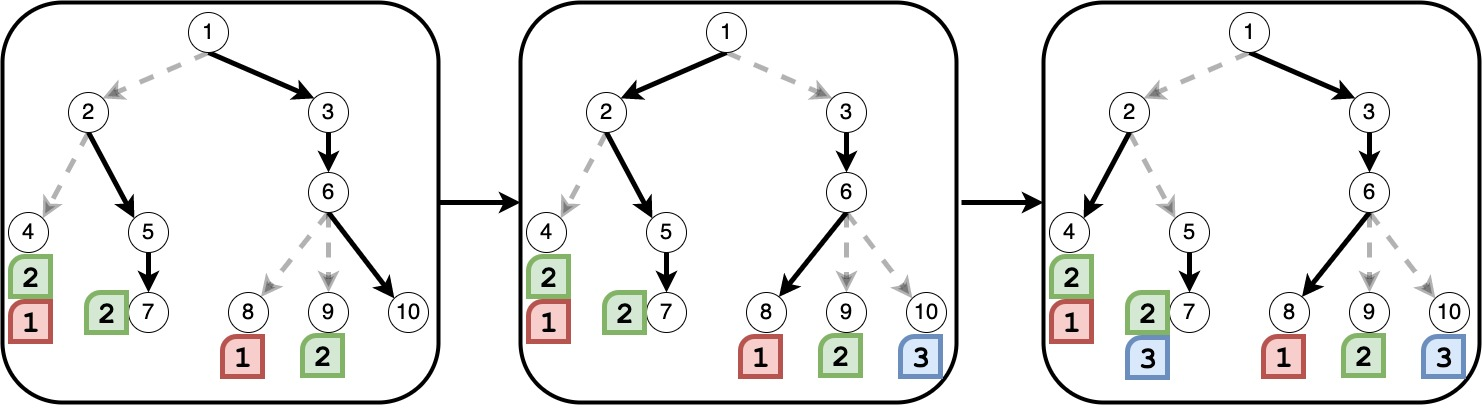
각 리프 노드에 쌓인 숫자를 모두 더해 배열로 나타내면 target과 같습니다.

트리의 각 노드들의 연결 관계를 담은 2차원 정수 배열 edges, 각 노드별로 만들어야 하는 숫자의 합을 담은 1차원 정수 배열 target이 매개변수로 주어집니다. 이때, target 대로 리프 노드에 쌓인 숫자의 합을 맞추기 위해 숫자를 떨어트리는 모든 경우 중 가장 적은 숫자를 사용하며 그중 사전 순으로 가장 빠른 경우를 1차원 정수 배열에 담아 return 하도록 solution 함수를 완성해주세요. 만약, target대로 숫자의 합을 만들 수 없는 경우 [-1]을 return 해주세요.

제한사항

• 1 ≤ edges의 길이 ≤ 100
  • edges[i]는 [부모 노드 번호, 자식 노드 번호] 형태로, 단방향으로 연결된 두 노드를 나타냅니다.
    • 1 ≤ 노드 번호 ≤ edges의 길이 + 1
  • 동일한 간선에 대한 정보가 중복해서 주어지지 않습니다.
  • 항상 하나의 트리 형태로 입력이 주어지며, 잘못된 데이터가 주어지는 경우는 없습니다.
  • 1번 노드는 항상 루트 노드입니다.
• target의 길이 = edges의 길이 + 1
  • target[i]는 i + 1번 노드에 쌓인 숫자의 합으로 만들어야 하는 수를 나타냅니다.
    • 0 ≤ 리프 노드의 target값 ≤ 100
    • 리프 노드를 제외한 노드의 target값 = 0
  • target의 원소의 합은 1 이상입니다.

입출력 예

edges	target	result
[[2, 4], [1, 2], [6, 8], [1, 3], [5, 7], [2, 5], [3, 6], [6, 10], [6, 9]]	[0, 0, 0, 3, 0, 0, 5, 1, 2, 3]	[1, 1, 2, 2, 2, 3, 3]
[[1, 2], [1, 3]]	[0, 7, 3]	[1, 1, 3, 2, 3]
[[1, 3], [1, 2]]	[0, 7, 1]	[-1]

풀이

참 어려운 문제인 것 같다.

문제를 이해해서 어떻게 노드에 숫자가 쌓이는지 까지는 구현을 했는데..

그러니까 방문하는 노드의 순서와 최소 몇번 이상 방문해야하는지, 혹은 최대로 몇번 방문할 수 있는 지 까지는 어떻게 혼자서 할 수 있었다.

그런데, 2번을 예로 들었을 때 노드를 [2, 3] 순서로 방문하고 최소 [2, 3, 2] 횟수로 방문해야 하며, 최대 [2, 3, 2, 3, 2, 3, 2] 방문 할 수 있다.

정확히 여기까지는 풀었는데...

여기서 부터 막혔다.
저 범위 안에서 노드에 숫자를 넣어야 하는데, 하나씩 다 넣고 맞춰보고 틀리면 다시 빼고 이런 식으로 하나씩 다하면 무조건 시간초과가 날테이니..

푸는 방법이 존재할 거라고 판단했고.

나는 답을 보지 않으면 절대로 그 방법을 생각 해낼 수 없다고 판단했따.

우선, 정답 풀이를 하자면 각 노드당 최소 최대 방문 횟수를 구하고 필수로 돌아야 하는 횟수가 최소 방문 횟수의 합이니, 최소 방문 횟수만큼은 움직인다.

대신 리프 노드는 방문하는 순서가 정해져 있으므로, 최소 방문 횟수안에서 중복으로 방문하는 경우가 발생한다.

이 때, 최대 방문 횟수보다 방문 횟수가 많아지면 정답을 만들 수 없다는 이야기이니 [-1] 을 리턴해준다.

그러면 최소 움직임일 때, 각 노드에 방문하는 횟수들이 정해진다.

이제는 노드들의 방문 횟수를 가지고, [1, 2, 3] 을 조건에 맞게 배치하여야 한다.

약간의 수학적 사고를 통해서 숫자를 배치한다.

예를 들어, 우리가 만들어야하는 숫자가 7일 때 우리가 방문하는 횟수는 3이라면..

[1, 3, 3], [2, 2, 3], [2, 3, 2], [3, 3, 1] 의 경우로 만들어 낼 수 있을 것이다.

이 중 사전적으로 가장 빠른 [1, 3, 3] 이 정답이 되겠다.

그럼 여기서 사전적으로 가장 빠르려면 3을 최대한 많이 써야 1을 2보다 많이 사용하게 된다.

그래서 만드려는 숫자 7에서 우리가 방문할 수 있는 횟수 3을 빼면 4가 남고, 이 4를 2로 나누면 2가 나온다.

즉 우리는 무조건 3번 방문해야하므로 [1, 1, 1] 을 기본으로 깔아놓고 시작한다.

그러면 우리는 4를 적절히 나눠 배치 해야하는데, 최대 숫자가 3이므로 1을 더하거나, 2를 더하거나 둘 중 하나만 선택해야한다.

그래서 3을 최대한 많이 만들기 위해서 2를 나누는 것이다.

만약 2로 나눴을 때 나머지가 생기면, 그 경우는 1을 더해야 하는 경우이므로 실제로는 2가 배치된다.

코드로 위 과정을 수행하게 되면
[] 빈 배열로 시작해서,
(7 - 3) / 2의 몫 만큼 3을 추가하고 → [3, 3]
나머지가 없으므로 2를 추가하는 것은 패스.
그럼 최소 방문 횟수를 맞춰줘야 하므로 1을 계속 추가한다. → [3, 3, 1]

이렇게 실제로는 마지막 숫자부터 추가가 되게 된다.

이걸 정답에 추가할 때, 우리가 위에서 구한 리프 노드 방문 순서대로 뒤에서 부터 꺼내어 추가하면 그게 답이다.

참.
어.
렵.
다.
.
.
.

코드

from collections import defaultdict, deque


def solution(edges, target):
    answer = []

    tree = defaultdict(list)
    for s, e in edges:
        tree[s].append(e)
    for i in tree.keys():
        tree[i].sort()

    min_visit, max_visit = create_min_max(target)
    node_visit, visit = create_node_visit(tree, min_visit, max_visit)
    if node_visit == [-1]:
        return [-1]
    node_nums = create_node_nums(target, node_visit)

    for node in visit:
        answer.append(node_nums[node].pop())

    print(answer)

    return answer


def create_min_max(target):
    min_visit = defaultdict(int)
    max_visit = defaultdict(int)

    for node, visit in enumerate(target, 1):
        max_visit[node] = visit

        quotient, remainder = divmod(visit, 3)
        if remainder:
            quotient += 1
        min_visit[node] = quotient

    return min_visit, max_visit


def create_node_visit(tree, min_visit, max_visit):
    node_child_index = defaultdict(int)
    node_visit = defaultdict(int)
    required_visit = sum(min_visit.values())
    visit = []
    while required_visit:
        parent = 1
        while tree[parent]:
            index = node_child_index[parent]
            child = tree[parent][index]
            index += 1

            if index == len(tree[parent]):
                index = 0

            node_child_index[parent] = index

            parent = child

        node_visit[parent] += 1
        visit.append(parent)
        if node_visit[parent] <= min_visit[parent]:
            required_visit -= 1

        elif max_visit[parent] < node_visit[parent]:
            return [-1], visit

    return node_visit, visit

def create_node_nums(target, node_visit):
    node_nums = defaultdict(list)
    for node, t in enumerate(target, 1):
        nums = []
        three, two = divmod(t - node_visit[node], 2)

        for _ in range(three):
            nums.append(3)
        if two:
            nums.append(2)

        while len(nums) < node_visit[node]:
            nums.append(1)

        node_nums[node] = nums

    return node_nums