프로그래머스 숫자 변환하기 JAVA

문제

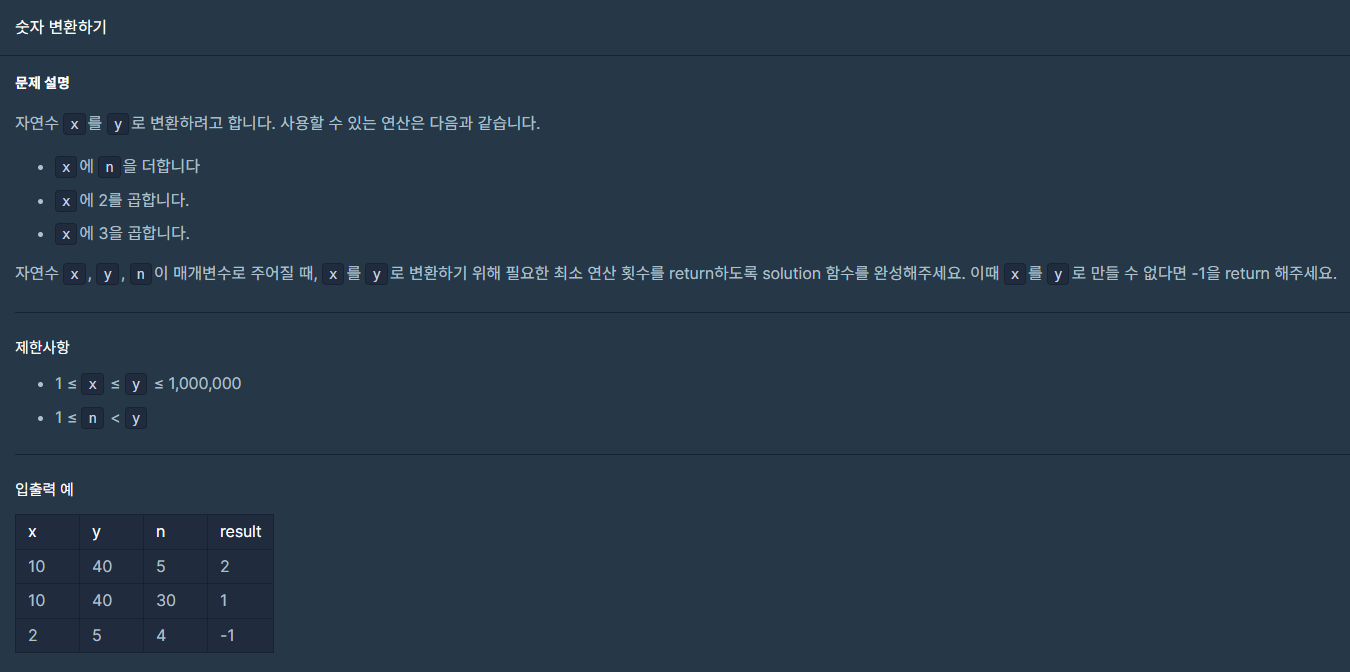
리뷰

처음에는 bfs로 풀어야 하나 싶었다.
그런데 bfs로 풀려면 재귀함수가 백트래킹 조건이 필요한데, 백트래킹 조건을 어떻게 세워야 하는가에서 막혔다.
x*2,x*3,x+5 이런식으로 x에서 더하거나 곱해나간다는 전제로 생각해서 더 그랬던거 같다.
결국 생각해보다가 dp로 풀이된게 있어서 그걸 참고했다.

x부터 1씩 숫자를 증가시켜 가면서 해당 숫자가 각 연산 방법에 의해 만들어질 수 있다면,
그 숫자를 만들기 위해 필요한 연산 횟수 중에 최소 횟수를 누적해 가면 된다.
여기서 각 숫자에 대한 연산 횟수를 저장하기 위한 배열이 필요하다.

이해는 했지만 비슷한 문제가 나온다면 내가 응용해서 풀 수가 있을까...?
 

풀이

	// i가 만들어질 수 없는 수일 때 max값을 저장
	static int MAX = Integer.MAX_VALUE;

    public int solution(int x, int y, int n) {
        int answer = 0;
		
        //y만큼의 크기를 가진 배열을 선언
        int dp[] = new int[y+1];
		
        // x를 1씩 증가시킬 때 각 숫자가 연산 방법에 의해 만들어질 수 있는 수인지 확인하기 위한 반복문
        for(int i = x+1; i < y+1; i++){
        	// i가 x*2 연산으로 만들어질 때를 저장할 변수
            int a = MAX;
            // i가 x*3 연산으로 만들어질 때를 저장할 변수
            int b = MAX;
            // i가 x+5 연산으로 만들어질 때를 저장할 변수
            int c = MAX;
			
            // i가 2로 나눠지고, 그 숫자가 x보다 클 때
            // (x보다 작은 숫자는 연산 방법으로 만들어질 수 없으므로)
            if(isDivide(i, 2) && ((i/2) >= x)){
                a = dp[i/2];
            }
            if(isDivide(i,3) && ((i/3) >= x)){
                b = dp[i/3];
            }
            if((i-n) >= x){
                c = dp[i-n];
            }
			
            // 해당 숫자를 만드는 방법 중 최소한의 연산 수를 저장해야하기 때문에 min메서드를 사용하여 비교
            int min = Math.min(a,b);
            min = Math.min(min,c);
			
            // 해당 숫자가 각 연산 방법으로 만들어지는 수일 때 기존 연산 수 +1을 현재 위치에 저장
            // 만들어지지 않을 경우 최대값 저장
            dp[i] = (min < MAX) ? min+1 : MAX;
        }
        
		// dp[y]의 값이 최대값보다 작다면 y는 연산에 의해 만들어질 수 있는 수이므로 dp[y]를 출력
        // 최대값이라면 만들어질 수 없는 숫자이므로 -1을 출력
        answer = (dp[y] < MAX) ? dp[y] : -1;

        return answer;
    }
	
    
    // x부터 1씩 증가하는 변수인 i가 각 연산에 의해 나올 수 있는 수인지 확인하는 메서드
    public static boolean isDivide(int i, int n){
        if(i/n > 0 && i%n == 0){
            return true;
        }
        return false;
    }