Algorithm(빅오 표기법:Big-O Notation)

Big-O 표기법이란?

• 알고리즘의 효율성을 수학적으로 표기하는 방식
• 시간과 공간 복잡도를 표현
• 데이터 증가에 따른 알고리즘 성능 측정에 목적

Big-O 표기법의 종류

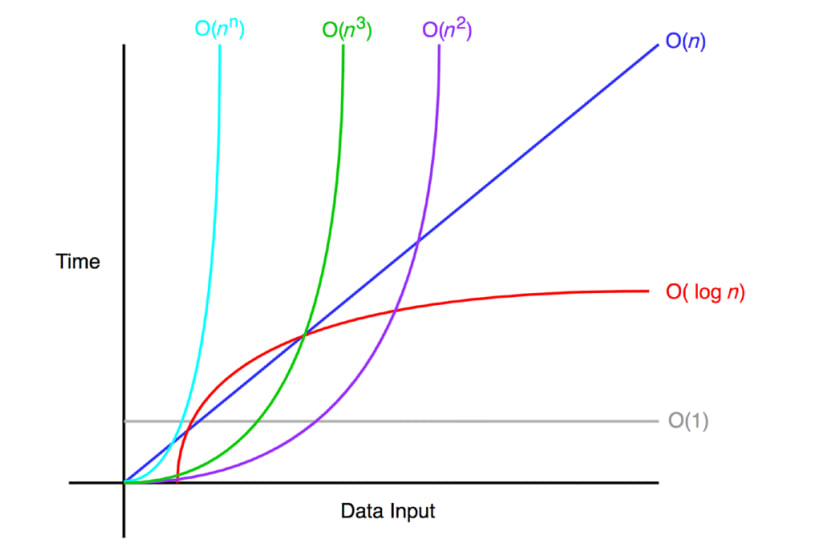
O(1)

각 인풋 공간에 변화가 없다.
그래서 constant(변함없는) time라 부른다.

function exampleConstant(n) {
    return n*n;
}

O(N)

linear time이라고 하며, 최악의 경우 n개의 연산을 수행해야 할 경우 적용된다.
대부분 간단한 반복문 안에서 constant time연산을 하는 경우이다.

function exampleLinear(n) {
    for (var i = 0 ; i < n; i++ ) {
        console.log(i)
    }
}

O(log(n))

Logarithmic time 함수는 실행시간이 입력크기의 로그에 비례한다.

function log(n) {
    for (let i = 1; i < n; i*=2) {
        const result = i;
        console.log(result);  
    }
}

위 코드에서 어떤 반복에서도 i = 2n의 값을 볼 수 있으므로 n번째 반복에서는 i = 2n의 값을 볼 수 있다.
또한, i의 값이 항상 루프 자체의 크기(N)보다 작다는 것을 알고 있다.

그러므로 이 결과를 추론할 수 있다.
2n < N
log(2n) < log(N)
n < log(N)

반복횟수가 항상 입력크기에 대한 로그보다 적다는 것을 알 수 있다.
그러므로, 알고리즘의 최악의 경우는 O(logN)이다.
Logarithmic 시간 복잡도의 효율성은 백만개의 인풋같이 큰 경우 명백하게 드러난다.

O(n2)

Quadratic time 알고리즘에서는 시간복잡도의 어두운 면을 보게 된다.
이름에서 알 수 있듯이, 인풋의 크기에 따라 2차식으로 속도에 영향을 끼친다.
가장 평범한 예시는 이중 반복문이다.

for (int i = 0; i <n; i += c) {
    for (int j = 0; j < n; j += c) {
    // some O(1) expressions
    }
}

안에 있는 반복문은 밖에 있는 반복문의 값과 상관없이 항상 n번 실행된다.
그러므로 O(n2)의 시간 복잡도를 갖는다.

Reference

• understanding big O notation with js
• 빅오표기법 완전정복