
🔥 짧고 굵은 python 전용 코테 cheat sheet 입니다. 정리 및 리마인드겸 작성했습니다.
🔥 [25.07월 최종 수정]
Coding Test Algorithm
빠른 찾기와 리마인드를 위한, python 코딩테스트 전용 cheat sheet
설명을 위한 글X, 스크롤 압박 주의!!
1. 초중급 알고리즘 종류, intro
- PS분야 관점보다는 철저하게 코딩테스트 관점에서 나오는 자료구조, 알고리즘 종류들
- 사실 자료구조 자체가 기초 알고리즘을 기반으로 설계되었기 때문에 둘을 완전 분리하는 것은 어불성설 일 수 있으나, 기본적으로 바로 활용가능한 자료구조는 알고리즘과 구분했다.
1) Stack/Queue
- 알고리즘 종류라기 보단 자료구조다.
- Que는 python에서
deque쓰는게 좋음 - 괄호 없애기, 후위 연산 / 시계 방향의 배열 순환 거의 큐 (공주 구하기)
from collections import deque
# Stack - 괄호 검증
def is_valid_parentheses(s):
stack = []
pairs = {'(': ')', '[': ']', '{': '}'}
for char in s:
if char in pairs:
stack.append(char)
elif stack and pairs[stack[-1]] == char:
stack.pop()
else:
return False
return not stack
# Queue - 요세푸스 문제 (공주 구하기)
def josephus(n, k):
queue = deque(range(1, n + 1))
while len(queue) > 1:
for _ in range(k - 1):
queue.append(queue.popleft())
queue.popleft()
return queue[0]2) Hash
- 알고리즘 종류라기 보단 자료구조다.
- 중복 제거, 최적화,
- 완주하지 못한 선수
# 완주하지 못한 선수
def solution(participant, completion):
hash_dict = {}
for person in participant:
hash_dict[person] = hash_dict.get(person, 0) + 1
for person in completion:
hash_dict[person] -= 1
for person in hash_dict:
if hash_dict[person] > 0:
return person
# 두 수의 합
def two_sum(nums, target):
hash_map = {}
for i, num in enumerate(nums):
complement = target - num
if complement in hash_map:
return [hash_map[complement], i]
hash_map[num] = i3) Heap (P.Q)
- 알고리즘 종류라기 보단 자료구조다.
- 완전 이진 트리의 성질을 만족하는 자료구조, 우선순위 큐를 위하여 만들어진 자료구조이다. -> 여러 개의 값들 중에서 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
- insert 하는 순간에 대소비교를 하며 노드추가를 하니 최악은 O(logN) 이다. 그래서 P.Q를
for loop하나와 같이 응용하는 경우O(NlogN)이며 중첩for loop대신(O(N^2))최적화를 한다고 생각하자. - python P.Q는 기본라이브러리
heapq를 활용
import heapq
# 최소 힙 - K번째 최소값 찾기
def find_kth_smallest(nums, k):
heapq.heapify(nums)
for _ in range(k - 1):
heapq.heappop(nums)
return heapq.heappop(nums)
# 최대 힙 - K번째 최대값 찾기 (음수 활용)
def find_kth_largest(nums, k):
max_heap = [-num for num in nums]
heapq.heapify(max_heap)
for _ in range(k - 1):
heapq.heappop(max_heap)
return -heapq.heappop(max_heap)4) Sorting
- 선택, 삽입, 버블, 합병(병합), 힙(tree), 퀵 까지는 기본 소양이다.
- n^2 / nlogn / 메모리 복잡도에 대한 개념은 있어야 한다.
- sorting 자체의 문제보다는 PS에 데이터 정렬이 필요한가? 정도를 알아차리는게 또 중요한 것 같다.
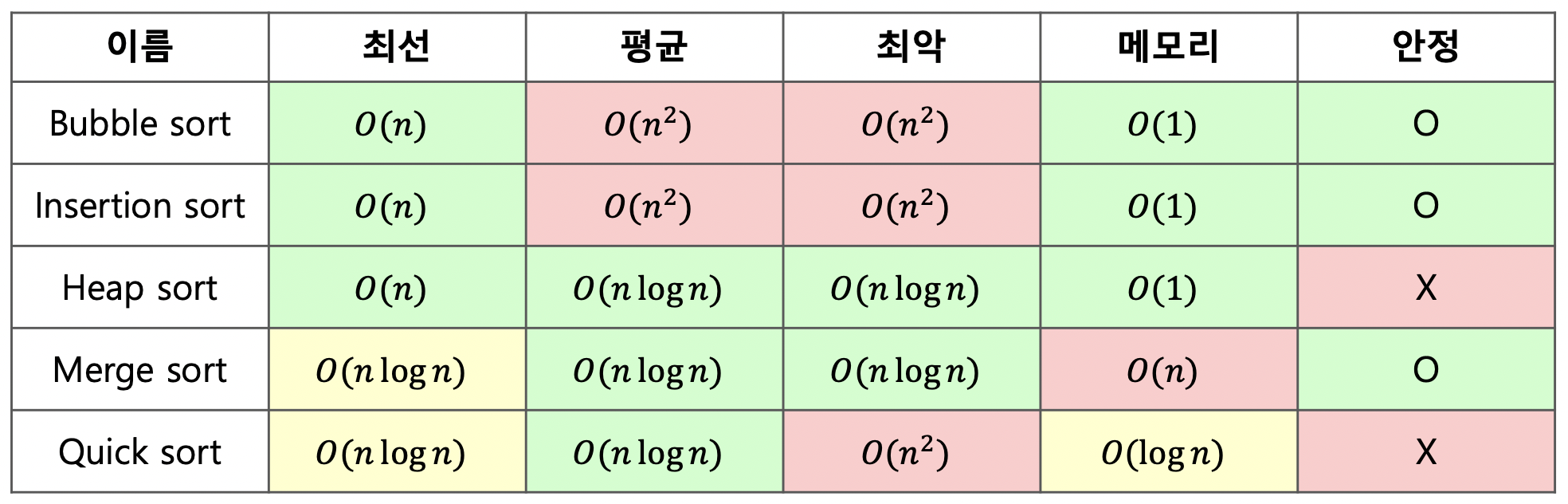
- 또 추가로 생각할 부분은, 메모리 복잡도가 크지 않다면, 계수 정렬 를 (index + counter) 사용하는 접근 법도 좋다.
O(N)
# 퀵 정렬
def quick_sort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2]
left = [x for x in arr if x < pivot]
middle = [x for x in arr if x == pivot]
right = [x for x in arr if x > pivot]
return quick_sort(left) + middle + quick_sort(right)
# 병합 정렬
def merge_sort(arr):
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result5) implementation, simulation
- Brute force / 완전 탐색의 형태가 많다. 단순 완탐의 접근법에 대해 기본적으로 다 알고 있어야 한다. 사실 단순 구현은 거의 보기 힘들고, 구현 + 다른 알고리즘 개념이 대부분이다.
- "simulation" 은 "문제에서 제시한 방법을 step by step 으로 직접 수행"하는 경우를 말한다.
- 어떻게 되었든 "구현"은 피지컬이 꽤 중요하다. 하지만 python에서는 자료형을 명시하지 않기 때문에 데이터 개수 - list 길이에 따라 얼마나 메모리 복잡도가 높은지 꼭 기억하고 있어야 한다.
- 1,000 - 약 4KB / 1,000,000 - 약 4MB / 10,000,000 - 약 40MB
- 나이트가 움직일 수 있는 경우의 수
# 나이트 이동 경우의 수
def knight_moves(x, y, n):
moves = [(2, 1), (2, -1), (-2, 1), (-2, -1),
(1, 2), (1, -2), (-1, 2), (-1, -2)]
count = 0
for dx, dy in moves:
nx, ny = x + dx, y + dy
if 0 <= nx < n and 0 <= ny < n:
count += 1
return count
# 시뮬레이션 - 로봇 이동
def robot_move(commands, obstacles):
x, y = 0, 0
direction = 0 # 0: 북, 1: 동, 2: 남, 3: 서
dx = [0, 1, 0, -1]
dy = [1, 0, -1, 0]
obstacle_set = set(map(tuple, obstacles))
for command in commands:
if command == "G":
nx = x + dx[direction]
ny = y + dy[direction]
if (nx, ny) not in obstacle_set:
x, y = nx, ny
elif command == "L":
direction = (direction - 1) % 4
elif command == "R":
direction = (direction + 1) % 4
return [x, y]6) Greedy (탐욕법)
- "그 순간 최선"을 다하는게 "최적"이라는, 내가 생각하기에 가장 어려운 개념을 가진 유형이다.
- 그리디 해결이 어떻게 항상 최적의 해를 보장할 수 있는지, "정당한지 검토할 수 있는 것" 이 핵심
- "교환 논증(Exchange Argument)", 귀납적으로 증명되는 개념 - 위키
- 거스름돈 (큰 단위가 항상 작은 단위의 배수 -> 작은 단위 종합해 다른 해가 나올 수 없기 때문) / 강의실 배정
# 거스름돈 문제
def min_coins(amount, coins):
coins.sort(reverse=True)
count = 0
for coin in coins:
count += amount // coin
amount %= coin
return count if amount == 0 else -1
# 회의실 배정
def meeting_rooms(meetings):
meetings.sort(key=lambda x: x[1]) # 끝나는 시간 기준 정렬
count = 0
last_end_time = 0
for start, end in meetings:
if start >= last_end_time:
count += 1
last_end_time = end
return count7) DP
- 큰 문제를 작게 나누고, 같은 문제는 한 번만 풀자 / 최적화를 "메모리 관점"에서 가져가는 것, 중복되는 연산을 줄이는 것 / dynamic programing, 그리고 이를 위한 memoization(caching). 접근법은 top-down, bottom-up이 있다.
- 간단한 점화식 세우기는 쉬울지 몰라도 DP를 기본개념으로 상위 개념의 알고리즘까지 쭉 관통하는 개념이라 상대적으로 어렵다고 생각한다.
- 그리고 좀 더 복잡한 알고리즘 (완전탐색 + DP, 중복 방문-탐색에 대한 제한, DP) 을 나아가기위한 초석이다.
- 피보나치, 수열, n번째 수, 1로 만들기, 개미 전사, 바닥 공사 (타일링 문제), 효율적 화폐 구성(그리디 인척) 등
# 피보나치 수열
def fibonacci(n):
if n <= 1:
return n
dp = [0] * (n + 1)
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
# 1로 만들기
def make_one(n):
dp = [0] * (n + 1)
for i in range(2, n + 1):
dp[i] = dp[i-1] + 1
if i % 2 == 0:
dp[i] = min(dp[i], dp[i//2] + 1)
if i % 3 == 0:
dp[i] = min(dp[i], dp[i//3] + 1)
return dp[n]8) Graph
- 알고리즘 종류라기 보단 자료구조다.
- 그래프는 쉽게 말하자면 "노드와 노드를 연결하는 간선(edge)" 으로 이뤄진 자료구조다. 인접행렬과 인접 연결리스트 형태로 표현이 가능하다. 조금 더 상위 자료구조로 가기위한 첫 스탭.
- 종류가 워낙다양하고 그래프 자체만 문제로 나오진 않는다. 가장 흔하게는 그래프에서 [ DFS/BFS 탐색 + 조건 ] 정도 형태이다. 가중치가 있는 것은 탐색 순서에도 영향을 주니 기억!
- 주기(cycle, 경로의 시작과 끝 노드가 같은 경로)가 없는 연결된 그래프를 "트리(tree)"라고 한다.
# 인접 리스트로 그래프 표현
def create_graph(edges, n):
graph = [[] for _ in range(n)]
for a, b in edges:
graph[a].append(b)
graph[b].append(a) # 무방향 그래프
return graph
# 인접 행렬로 그래프 표현
def create_matrix_graph(edges, n):
graph = [[0] * n for _ in range(n)]
for a, b in edges:
graph[a][b] = 1
graph[b][a] = 1 # 무방향 그래프
return graph9) DFS / BFS
- 깊이 우선 탐색 (stack, recursive)과 너비 우선 탐색 (queue, - deque) / "완전 탐색" 이 기본 원리임을 잊으면 안된다.
- 단순 탐색은 거의 안보이고 "map형태에서 상-하-좌-우 탐색 + 조건"의 문제가 가장 흔하다.
from collections import deque
# DFS - 재귀
def dfs_recursive(graph, start, visited):
visited[start] = True
print(start, end=' ')
for neighbor in graph[start]:
if not visited[neighbor]:
dfs_recursive(graph, neighbor, visited)
# BFS
def bfs(graph, start):
visited = [False] * len(graph)
queue = deque([start])
visited[start] = True
while queue:
node = queue.popleft()
print(node, end=' ')
for neighbor in graph[node]:
if not visited[neighbor]:
visited[neighbor] = True
queue.append(neighbor)
# 미로 탈출 (BFS)
def maze_escape(maze):
n, m = len(maze), len(maze[0])
queue = deque([(0, 0, 1)]) # (x, y, distance)
visited = [[False] * m for _ in range(n)]
visited[0][0] = True
dx = [-1, 1, 0, 0]
dy = [0, 0, -1, 1]
while queue:
x, y, dist = queue.popleft()
if x == n-1 and y == m-1:
return dist
for i in range(4):
nx, ny = x + dx[i], y + dy[i]
if (0 <= nx < n and 0 <= ny < m and
maze[nx][ny] == 1 and not visited[nx][ny]):
visited[nx][ny] = True
queue.append((nx, ny, dist + 1))
return -110) Binary Search
- 순서가 이미 있는, 즉 정렬되어 있는 배열(또는 object, list) 대상으로 해당 값을 가지는 Index를 찾는 알고리즘
- 검색 범위를 절반씩 줄여서 접근하여
O(N)이 걸릴 탐색을O(logN)으로 줄여준다. - Parametric Search 는 "주어진 범위 내에서 원하는 값 또는 원하는 조건에 가장 일치하는 값을 찾아내는 알고리즘" 이다. 최적화 문제를 결정 문제로 바꾸는 것. 이런 형태의 문제를 이진 탐색으로 해결한다.
- 떡볶이 떡 만들기, 2개 짝 세기 (아래)
# 기본 이진 탐색
def binary_search(arr, target):
left, right = 0, len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
class Solution:
def countFairPairs(self, nums: List[int], lower: int, upper: int) -> int:
nums.sort() # O(n log n)
result = 0
for i in range(len(nums)):
# nums[i] + nums[j] >= lower => nums[j] >= lower - nums[i]
# nums[i] + nums[j] <= upper => nums[j] <= upper - nums[i]
min_val = lower - nums[i]
max_val = upper - nums[i]
# i+1부터 끝까지의 범위에서 [min_val, max_val] 사이의 값 개수 찾기
left_bound = bisect.bisect_left(nums, min_val, i + 1)
right_bound = bisect.bisect_right(nums, max_val, i + 1)
result += right_bound - left_bound
return result11) Binary Search Tree
- Tree중에 자식노드가 최대 두 개인 노드들로 구성된 트리를 "이진트리"라고 한다.
- 이진트리에는 정이진트리(full binary tree), 완전이진트리(complete binary tree), 균형이진트리(balanced binary tree) 등이 있다.
- 모든 왼쪽 자식의 값이 루트나 부모보다 작고, 모든 오른쪽 자식의 값이 루트나 부모보다 큰 값을 가지는 특징을 가지는 이진트리가 "이진 탐색 트리"
- 왼쪽 자식 노드 값 < 부모 노드 값 < 오른쪽 자식 노드 값
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class BST:
def __init__(self):
self.root = None
def insert(self, val):
self.root = self._insert(self.root, val)
def _insert(self, node, val):
if not node:
return TreeNode(val)
if val < node.val:
node.left = self._insert(node.left, val)
else:
node.right = self._insert(node.right, val)
return node
def search(self, val):
return self._search(self.root, val)
def _search(self, node, val):
if not node or node.val == val:
return node
if val < node.val:
return self._search(node.left, val)
else:
return self._search(node.right, val)12) Backtracking
- 해를 찾는 도중 해가 아니어서 막히면, 되돌아가서 다시 해를 찾아가는 기법
- 그 해를 찾는 과정 중에 어긋나면 아예 그 길로 가지 않는다는 원리다. 최적화 에서 중요하다. DFS의 예로, 깊이로 가는 중 하나라도 어긋나면 그 깊이까지 갈 이유가 전혀 없어진다. 이렇게 경우의 수를 확실하게 줄여 최적화를 한다. -> 모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만 살펴보는 것 / promising 이라고 표현한다.
- N번째 Queen
# N-Queen 문제
def n_queens(n):
def is_safe(board, row, col):
for i in range(row):
if board[i] == col or \
board[i] - i == col - row or \
board[i] + i == col + row:
return False
return True
def solve(board, row):
if row == n:
return [board[:]]
solutions = []
for col in range(n):
if is_safe(board, row, col):
board[row] = col
solutions.extend(solve(board, row + 1))
return solutions
return solve([0] * n, 0)
# 부분집합 생성
def generate_subsets(nums):
result = []
def backtrack(start, path):
result.append(path[:])
for i in range(start, len(nums)):
path.append(nums[i])
backtrack(i + 1, path)
path.pop()
backtrack(0, [])
return result13) LIS / LCS
- Longest Increasing Subsequence(최장 증가 부분 수열) / Longest Common Subsequence(최장 공통 부분 수열) / 개념은 간단하지만 어떨때 해당 해법을 활용할지 판단하는게 쉽지않다.
- 기본적으로 부분 수열 구하기에 DP를 얹은 형태다. 하지만 그래도
O(N^2)이다. 그래서 이분탐색 을 활용해 최적화를 한다. - 반도체 설계
# LIS - O(N^2) DP 버전
def lis_dp(arr):
n = len(arr)
dp = [1] * n
for i in range(1, n):
for j in range(i):
if arr[j] < arr[i]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
# LIS - O(N log N) 이진탐색 버전
# tails[i]는 길이 i+1인 증가 부분수열의 가장 작은 마지막 원소를 저장.
# 새 원소가 오면 이진탐색으로 교체할 위치를 O(log n)에 찾음
import bisect
def lis_binary_search(arr):
tails = []
for num in arr:
pos = bisect.bisect_left(tails, num)
if pos == len(tails):
tails.append(num)
else:
tails[pos] = num
return len(tails)
# LCS
def lcs(text1, text2):
m, n = len(text1), len(text2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if text1[i-1] == text2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[m][n]14) Dijkstra / Floyd-Warshall
- 보통 "최단거리"를 구하기 위해서 사용하는 알고리즘이다.
- 다익스트라는 한 지점에서 다른 특정 지점(모든 다른 지점)까지 최단 경로 인 반면, 플로이드워셜은 모든 지점에서 다른 모든 지점까지의 최단 경로 에 대해 알 수 있다.
- 다익스트라는 "그리디" 특성을 가지고, 플로이드워셜은 "DP"의 특성을 가진다.
import heapq
# 다익스트라 알고리즘
def dijkstra(graph, start):
distances = {node: float('inf') for node in graph}
distances[start] = 0
pq = [(0, start)]
while pq:
current_distance, current_node = heapq.heappop(pq)
if current_distance > distances[current_node]:
continue
for neighbor, weight in graph[current_node]:
distance = current_distance + weight
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(pq, (distance, neighbor))
return distances
# 플로이드-워셜 알고리즘
def floyd_warshall(graph):
n = len(graph)
dist = [[float('inf')] * n for _ in range(n)]
# 초기화
for i in range(n):
dist[i][i] = 0
for i in range(n):
for j in range(n):
if graph[i][j] != 0:
dist[i][j] = graph[i][j]
# 플로이드-워셜
for k in range(n):
for i in range(n):
for j in range(n):
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])
return dist15) Divide and Conquer
- 분할정복, 큰 부분을 작은 부분으로 나누어 해결하고, 작은 부분의 각 해결을 결합해 결국 전체 문제를 해결하는 방식, 아래 3가지 단계를 따른다. 알고리즘 분류의 큰 패러다임 중 하나다.
- 분할(
Divide): 원래 문제를 동일한 유형의 작은 하위 문제로 분할합니다. - 정복(
Conquer): 각 하위 문제를 재귀적으로 해결합니다. 하위 문제가 충분히 작으면 직접적인 방법으로 해결합니다. - 결합(
Combine): 하위 문제의 해결 방법을 결합하여 원래 문제의 해결 방법을 도출합니다.
- 퀵 정렬(Quick Sort), 이진 검색(Binary Search), 합병 정렬(Merge Sort), 최대 부분 배열 문제(Maximum Subarray Problem)
# 최대 부분 배열 합 (Maximum Subarray)
def max_subarray(nums):
def divide_conquer(left, right):
if left == right:
return nums[left]
mid = (left + right) // 2
# 왼쪽 최대값
left_max = divide_conquer(left, mid)
# 오른쪽 최대값
right_max = divide_conquer(mid + 1, right)
# 중간을 포함하는 최대값
left_sum = float('-inf')
total = 0
for i in range(mid, left - 1, -1):
total += nums[i]
left_sum = max(left_sum, total)
right_sum = float('-inf')
total = 0
for i in range(mid + 1, right + 1):
total += nums[i]
right_sum = max(right_sum, total)
cross_max = left_sum + right_sum
return max(left_max, right_max, cross_max)
return divide_conquer(0, len(nums) - 1)
# 거듭제곱 (분할정복)
def power(base, exp):
if exp == 0:
return 1
if exp == 1:
return base
if exp % 2 == 0:
half = power(base, exp // 2)
return half * half
else:
return base * power(base, exp - 1)16) Topological Sort
- 사이클이 없는 방향 그래프에서, "순서가 정해져있는 작업"을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용하는 알고리즘 / 유일해가 아님
- 사이클 검출: Kahn 알고리즘에서 처리된 노드 수가 전체 노드 수보다 적으면 사이클 존재
from collections import deque, defaultdict
def topological_sort(n, edges):
graph = defaultdict(list)
indegree = [0] * n
# 그래프와 진입차수 구성
for a, b in edges:
graph[a].append(b)
indegree[b] += 1
# 진입차수가 0인 노드를 큐에 추가
queue = deque()
for i in range(n):
if indegree[i] == 0:
queue.append(i)
result = []
while queue:
node = queue.popleft()
result.append(node)
# 연결된 노드들의 진입차수 감소
for neighbor in graph[node]:
indegree[neighbor] -= 1
if indegree[neighbor] == 0:
queue.append(neighbor)
return result if len(result) == n else [] # 사이클 존재 시 빈 리스트
# DFS 기반 위상정렬 (역후위순회)
def topological_sort_dfs(graph):
visited = set()
rec_stack = set() # 현재 경로의 노드들
result = []
def dfs(node):
if node in rec_stack: # 사이클 발견
return False
if node in visited:
return True
visited.add(node)
rec_stack.add(node)
for neighbor in graph[node]:
if not dfs(neighbor):
return False
rec_stack.remove(node)
result.append(node) # 후위순회 시점에 추가
return True
# 역순이 위상정렬 결과
return result[::-1] if all(dfs(node) for node in graph) else []17) Union-Find
- 서로소 집합(Disjoint Set)을 효율적으로 관리하는 자료구조로, 특정 원소들이 같은 집합에 속하는지 여부를 빠르게 확인할 수 있다.
Find연산에서 경로 압축(Path Compression),Union연산에서 랭크 기반 병합(Union by Rank) 을 통해 거의 상수 시간에 집합 연산이 가능하다.- "사이클 판별" 문제에서, 그래프의 간선을 하나씩 연결해보면서 이미 연결된 두 노드를 다시 연결하려 할 경우 사이클이 생긴다는 것을 Union-Find로 빠르게 판별할 수 있다.
- ex) 부모 찾기 / 집합의 표현 / 친구 네트워크
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x]) # 경로 압축
return self.parent[x]
def union(self, x, y):
px, py = self.find(x), self.find(y)
if px == py:
return False
# Union by rank
if self.rank[px] < self.rank[py]:
px, py = py, px
self.parent[py] = px
if self.rank[px] == self.rank[py]:
self.rank[px] += 1
return True
def connected(self, x, y):
return self.find(x) == self.find(y)
# 사이클 판별
def has_cycle(n, edges):
uf = UnionFind(n)
for a, b in edges:
if uf.connected(a, b):
return True
uf.union(a, b)
return False18) MST(Minimum Spanning Tree)
- Spanning Tree (신장트리)는 최소 연결 부분 그래프 이다. 최소 연결이란 말은 "간선의 수가 가장 적다"는 말이다. 한 그래프에서 다양한 신장트리가 존재한다.
- Kruskal Algorithm (그리디 특성) / Prim MST Algorithm 을 활용해서 최소 신장 트리를 찾는다.
# Kruskal 알고리즘
def kruskal_mst(n, edges):
edges.sort(key=lambda x: x[2]) # 가중치 기준 정렬
uf = UnionFind(n)
mst = []
total_weight = 0
for a, b, weight in edges:
if uf.union(a, b):
mst.append((a, b, weight))
total_weight += weight
if len(mst) == n - 1:
break
return mst, total_weight
# Prim 알고리즘
def prim_mst(graph):
n = len(graph)
visited = [False] * n
min_heap = [(0, 0)] # (weight, node)
total_weight = 0
mst_edges = []
while min_heap:
weight, node = heapq.heappop(min_heap)
if visited[node]:
continue
visited[node] = True
total_weight += weight
for neighbor, edge_weight in graph[node]:
if not visited[neighbor]:
heapq.heappush(min_heap, (edge_weight, neighbor))
return total_weight19) Trie
- 문자열의 집합을 공통 접두사 기반으로 효율적으로 저장하고 탐색할 수 있는 트리 형태의 자료구조이다.
- 자동완성, 접두사 검색, 사전 정렬 등에 유용하며, 각 노드는 하나의 문자와 자식 노드 포인터들을 갖는다.
- "전화번호 목록" 문제에서, 한 번호가 다른 번호의 접두사가 되는 경우를 빠르게 판별해야 하는데, 이를 단순 비교 대신 Trie를 통해
O(L)시간에 체크할 수 있다. - 전화번호 목록 / 문자열 집합
class TrieNode:
def __init__(self):
self.children = {}
self.is_end = False
class Trie:
def __init__(self):
self.root = TrieNode()
def insert(self, word):
node = self.root
for char in word:
if char not in node.children:
node.children[char] = TrieNode()
node = node.children[char]
node.is_end = True
def search(self, word):
node = self.root
for char in word:
if char not in node.children:
return False
node = node.children[char]
return node.is_end
def starts_with(self, prefix):
node = self.root
for char in prefix:
if char not in node.children:
return False
node = node.children[char]
return True
# 전화번호 목록 문제
def phone_number_validation(phone_numbers):
trie = Trie()
for number in phone_numbers:
trie.insert(number)
for number in phone_numbers:
node = trie.root
for i, char in enumerate(number):
node = node.children[char]
if node.is_end and i < len(number) - 1:
return False # 접두사 발견
return True- 위에서 "공간복잡도 & 최적화" 를 위해 아래와 같이 접근 가능
# 공간복잡도: O(ALPHABET_SIZE × N × M)
# N: 문자열 개수, M: 평균 길이, ALPHABET_SIZE: 알파벳 크기
# 압축 트라이 최적화
class CompressedTrieNode:
def __init__(self):
self.children = {}
self.is_end = False
self.edge_label = "" # 간선에 문자열 저장해 공간 절약
# 메모리 절약:
# - 단일 자식 노드들을 하나로 압축
# - 빈도 기반 허프만 코딩과 유사한 최적화 가능20) Bit Manipulation (비트 연산)
- 자료 구조나 알고리즘이라기 보단 구현 또는 조건 처리에서 가장 빠르게 처리할 수 있는 케이스를 다룬다. (특히 부분집합/상태 표현, 조합 문제에서)
& (AND), | (OR), ^ (XOR), ~ (NOT), <<, >>- ex) 부분집합 생성 (2^N 개), 비트 마스크 DP, 집합 & 조합 문제 (ex. 외판원 순회)
# 부분집합 생성 (비트마스크)
def generate_subsets_bit(nums):
n = len(nums)
subsets = []
for mask in range(1 << n): # 2^n 개의 부분집합
subset = []
for i in range(n):
if mask & (1 << i): # i번째 비트가 1인지 확인
subset.append(nums[i])
subsets.append(subset)
return subsets
# 비트 연산 기본 함수들
def bit_operations(n):
# 특정 비트 설정
def set_bit(num, pos):
return num | (1 << pos)
# 특정 비트 제거
def clear_bit(num, pos):
return num & ~(1 << pos)
# 특정 비트 토글
def toggle_bit(num, pos):
return num ^ (1 << pos)
# 특정 비트 확인
def check_bit(num, pos):
return (num & (1 << pos)) != 0
return {
'set': set_bit(n, 2),
'clear': clear_bit(n, 2),
'toggle': toggle_bit(n, 2),
'check': check_bit(n, 2)
}
# 해밍 거리 (XOR 활용)
def hamming_distance(x, y):
xor = x ^ y
count = 0
while xor:
count += xor & 1
xor >>= 1
return count21) Sliding Window / Two Pointer
- 슬라이딩 윈도우에선 고정 & 가변 크기에 따라 다름
- 고정 크기: 윈도우 크기 K가 주어짐
- 가변 크기: 조건에 따라 윈도우 크기가 동적으로 변함
- 연속된 구간 합, 문자열 길이, 최적 구간 찾기 문제에 최적
O(N^2)brute-force 를O(N)으로 최적화 가능- 투 포인터는 정렬된 배열을 기반으로 하는 경우 많음 (이진탐색과도 잘 어울림)
- ex) 가장 긴 연속 부분 문자열, 특정 합을 만족하는 연속 부분 수열
# 슬라이딩 윈도우 - 최대 길이 부분 문자열
def longest_substring_without_repeating(s):
char_set = set()
left = 0
max_length = 0
for right in range(len(s)):
while s[right] in char_set:
char_set.remove(s[left])
left += 1
char_set.add(s[right])
max_length = max(max_length, right - left + 1)
return max_length
# 고정 크기 패턴
def fixed_window_pattern(arr, k):
window_sum = sum(arr[:k]) # 첫 윈도우 계산
max_sum = window_sum
for i in range(k, len(arr)):
# 슬라이딩: 새 원소 추가, 이전 원소 제거
window_sum += arr[i] - arr[i-k]
max_sum = max(max_sum, window_sum)
return max_sum
# 가변 크기 패턴 (조건 설정 방법)
def variable_window_pattern(arr, condition):
left = 0
for right in range(len(arr)):
# 윈도우 확장
add_to_window(arr[right])
# 조건 위반시 윈도우 축소
while violates_condition():
remove_from_window(arr[left])
left += 1
# 현재 윈도우에서 결과 업데이트
update_result()
# 투 포인터 - 두 수의 합
def two_sum_sorted(nums, target):
left, right = 0, len(nums) - 1
while left < right:
current_sum = nums[left] + nums[right]
if current_sum == target:
return [left, right]
elif current_sum < target:
left += 1
else:
right -= 1
return []
# 특정 합을 만족하는 연속 부분 수열
def subarray_sum(nums, target):
count = 0
current_sum = 0
left = 0
for right in range(len(nums)):
current_sum += nums[right]
while current_sum > target and left <= right:
current_sum -= nums[left]
left += 1
if current_sum == target:
count += 1
return count22) 몬테카를로 시뮬레이션(Monte Carlo Simulation)
- 확률적 문제를 해결하기 위해 무작위 샘플링을 반복적으로 수행하여 근사해를 구하는 통계적 방법
- 해석적으로 풀기 어려운 복잡한 수학적 문제나 확률 문제를 시뮬레이션을 통해 해결
- "큰 수의 법칙에 기반" -> 시행 횟수가 많을수록 이론값에 수렴
- 코딩테스트에서는 확률 계산, 기댓값 추정, 최적화 문제 등에 활용
- 무작위 샘플 생성: 문제 공간에서 랜덤하게 표본 추출
- 조건 검사: 각 샘플이 특정 조건을 만족하는지 확인
- 통계적 추정: 조건을 만족하는 비율로 확률/값 계산
- 수렴 확인: 충분한 시행으로 결과 안정화
import random
import math
# 원주율 π 추정 (가장 유명한 예시)
def estimate_pi(n_samples):
inside_circle = 0
for _ in range(n_samples):
x = random.uniform(-1, 1)
y = random.uniform(-1, 1)
# 원점에서 거리가 1 이하면 원 내부
if x*x + y*y <= 1:
inside_circle += 1
# π ≈ 4 × (원 내부 점의 비율)
return 4 * inside_circle / n_samples
# 확률 계산 (동전 던지기 연속 성공)
def consecutive_heads_probability(n_consecutive, n_trials=100000):
success = 0
for _ in range(n_trials):
consecutive_count = 0
max_consecutive = 0
for _ in range(100): # 100번 던지기
if random.random() < 0.5: # 앞면
consecutive_count += 1
max_consecutive = max(max_consecutive, consecutive_count)
else:
consecutive_count = 0
if max_consecutive >= n_consecutive:
success += 1
return success / n_trials
# 기댓값 계산
def expected_value_dice_sum(n_trials=100000):
total = 0
for _ in range(n_trials):
dice1 = random.randint(1, 6)
dice2 = random.randint(1, 6)
total += dice1 + dice2
return total / n_trials # 이론값: 72. Cheat Sheet
1) 복잡도 계산
시간 복잡도
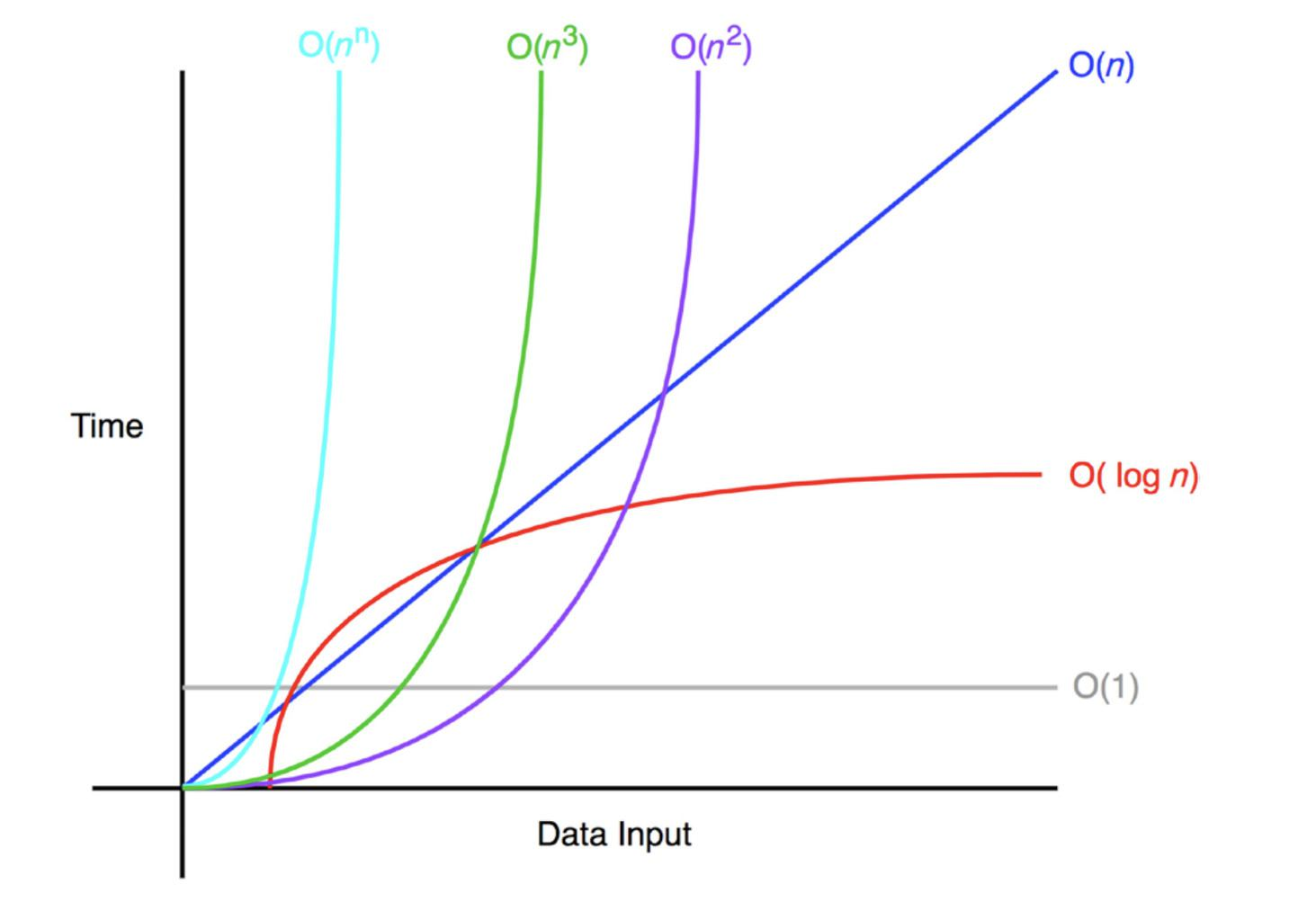

공간 복잡도
a: list[int] = [0] * 1000 # >= 4KB
a: list[int] = [0] * 1000000 # >= 4MB
a: list[list[int]] = [[0] * 2000] * 2000 # >= 16MB2) 코테 테크니컬 python tip
직접 input 받을 때
- 일반적으로 list, map 을 활용
# 공백을 기준으로 구분된 데이터를 입력 받을 떄
data = list(map(int, input().split()))
# 공백을 기준으로 구분된 데이터가 많지 않다면
a, b, c = map(int, input().split())- sys stdin을 활용해 빠른 input 받기 (꼭 직접 입력을 받아야 한다면, 추천)
import sys
# 공백으로 구분된 2개 숫자 입력 받기
N, M = map(int,sys.stdin.readline().split())
# 2차원 리스트 입력 받기
board = [list(map(int,sys.stdin.readline().split())) for _ in range(N)]
# 문자열 입력 받기
data = sys.stdin.readline().rstrip()- 사실 빠른 입출력 (I/O)는 아래와 같이 print, input 함수를 새로운 함수로 바인딩해버리자
import sys
input = sys.stdin.readline
print = sys.stdout.write
# sys.stdin.readline()은 개행문자 "\n"까지 읽어들이기 때문에
# .rstrip()등으로 지워주어야 하고
n = input() # "1"을 입력 할 때,
print(list(n)) # ['1', '\n']
print([int(n)]) # [1]
print(list(n.rstrip())) # ['1']
# print()는 출력 방식이 다음과 같이 바뀌어 버린다.
print("%s\n" % "123") # 123
print("%s\n" % ("12" + "3")) # 123
print("%d + %d = %d\n" % (1, 2, 1 + 2)) # 1 + 2 = 3문자열 아스키코드, 대소 문자
import string
string.ascii_lowercase # 소문자 abcdefghijklmnopqrstuvwxyz
string.ascii_uppercase # 대문자 ABCDEFGHIJKLMNOPQRSTUVWXYZ
string.ascii_letters # 대소문자 모두 abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ
string.digits # 숫자 0123456789
# str method tip
str.isupper()
str.islower()- 파이썬에서는 ljust, center, rjust와 같은 string의 메소드를 사용해 코드를 획기적으로 줄일 수 있습니다.
s = '가나다라'
n = 7
s.ljust(n) # 좌측 정렬
s.center(n) # 가운데 정렬
s.rjust(n) # 우측 정렬ZIP 활용, 2차원 배열, 열과 행 뒤집기
mylist = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
new_list = [[], [], []]
for i in range(len(mylist)):
for j in range(len(mylist[i])):
new_list[i].append(mylist[j][i])
# 위와 동일 #
list(map(list, zip(*mylist)))
# +a zip으로 list 2개 각 key:value 만들기
animals = ['cat', 'dog', 'lion']
sounds = ['meow', 'woof', 'roar']
answer = dict(zip(animals, sounds)) # {'cat': 'meow', 'dog': 'woof', 'lion': 'roar'}
# zip 함수에 서로 길이가 다른 리스트가 인자로 들어오는 경우에는 길이가 짧은 쪽 까지만 이터레이션이 이루어집니다.
def solution(mylist):
answer = []
for number1, number2 in zip(mylist, mylist[1:]):
answer.append(abs(number1 - number2))
return answer
if __name__ == '__main__':
mylist = [83, 48, 13, 4, 71, 11]
print(solution(mylist))
map 활용하기
# list element 모두 int 로 형 변환
list1 = ['1', '100', '33']
list2 = list(map(int, list1))
a = list(map(str, range(10)))
# ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
# input에서 map object 활용하기
>>> a = map(int, input().split())
10 20 (입력)
>>> a
<map object at 0x03DFB0D0>
>>> list(a)
[10, 20]
2차원 배열 1차원으로 만들기
my_list = [[1, 2], [3, 4], [5, 6]]
# 방법 1 - sum 함수
answer = sum(my_list, [])
# 방법 2 - itertools.chain
import itertools
list(itertools.chain.from_iterable(my_list))
# 방법 3 - itertools와 unpacking
import itertools
list(itertools.chain(*my_list))
# 방법 4 - list comprehension 이용
[element for array in my_list for element in array]
# 방법 5 - reduce 함수 이용 1
from functools import reduce
list(reduce(lambda x, y: x+y, my_list))
# 방법 6 - reduce 함수 이용 2
from functools import reduce
import operator
list(reduce(operator.add, my_list))
# 각 원소 길이가 모두 동일한 경우, numpy 사용가능
# 방법 7 - numpy 라이브러리의 flatten 이용
import numpy as np
np.array(my_list).flatten().tolist()
list에서 문자 등장 개수 count
import collections
my_list = [1, 2, 3, 4, 5, 6, 7, 8, 7, 9, 1, 2, 3, 3, 5, 2, 6, 8, 9, 0, 1, 1, 4, 7, 0]
answer = collections.Counter(my_list)
print(answer[1]) # = 4
print(answer[3]) # = 3
print(answer[100]) # = 0
for - (break) - else 구문
- for와 함께 쓰는 else는, for문이 중간에 break 등으로 끊기지 않고, 끝까지 수행 되었을 때 수행하는 코드를 담고 있습니다.
- 코딩을 하다 보면 for문이 중간에 break 되었는지, 되어있지 않는지 판별해야 되는 경우가 많이 있습니다.
테스트 변수(flag)를 둬서 확인하는 등으로 처리합니다. - 파이썬에서는 else의 사용으로 간단하게 해결할 수 있습니다. if문에 else를 사용하듯이 else를 사용 하게 됩니다. else의 들여쓰기는 for와 일치해야 합니다.
import math
if __name__ == '__main__':
numbers = [int(input()) for _ in range(5)]
multiplied = 1
for number in numbers:
multiplied *= number
if math.sqrt(multiplied) == int(math.sqrt(multiplied)):
print('found')
break
else:
print('not found')수 swap 하기
a = 3
b = 'abc'
temp = a
a = b
b = temp
# 아래와 같이 사용가능
a = 3
b = 'abc'
a, b = b, a 무한대와 비교하게, 항상 가장 작게, 항상 가장 크게
- 파이썬이 제공하는 inf 를 사용해보세요. inf는 어떤 숫자와 비교해도 무조건 크다고 판정됩니다.
min_val = float('inf')
min_val > 10000000000
# inf에는 음수 기호를 붙이는 것도 가능합니다.
max_val = float('-inf')진수 변환기
tmp = string.digits + string.ascii_lowercase
def convert(num, base):
q, r = divmod(num, base)
if q == 0:
return tmp[r]
else:
return convert(q, base) + tmp[r]
# --------------------------------------------- #
def solution(n):
tmp = ''
while n:
tmp += str(n % 3)
n = n // 3
answer = int(tmp, 3)
return answerint(문자열, 진수)로 특정 "진수"로 되어있는 "문자열"을 10진수로 바꾼다.
빠르게 문자열 중복 제거
dict.fromkeys()활용
# 기본 사용법
dict.fromkeys(iterable, value=None)
# 예시
dict.fromkeys(['a', 'b', 'a', 'c']) # {'a': None, 'b': None, 'c': None}
dict.fromkeys('hello', 0) # {'h': 0, 'e': 0, 'l': 0, 'o': 0}
# 아래와 같이 함수화 해서 사용하면 bb
def remove_duplicates(s: str | list) -> str:
return ''.join(dict.fromkeys(s))- 퍼포먼스는? 사실 "해시테이블" 을 사용하는 것.
- cpython 기준
dict_fromkeys_impl로 C언어로만 구현되어 있음, https://github.com/python/cpython/blob/d8fa40b08da60a711311751891fa830cb4ae77f3/Objects/dictobject.c#L3200
3) 코테에 필요한 기본 수학 상식
약수: 어떤 수를 나누어떨어지게 하는 수
-
약수가 홀수개인 모든 수는 제곱수
-
제곱수가 아닌 수는 약수가 짝수개
-
소수: 1과 자기 자신만으로 나누어지는 수
# 소수 찾기 아라토테네스의 채
def solution(n):
MAX_NUM = 1_000_000
answer = 0
d = [True]*MAX_NUM
d[0] = False
d[1] = False
d[2] = True
for i in range(2, n + 1):
if d[i]:
answer += 1
for j in range(2, n + 1):
if (j * i) >= MAX_NUM:
break
d[j * i] = False
return answer최대공약수(GCD, Greateast Common Division)와 최소공배수(LCM, Least Common Multiple)

A,B 의 최대공약수를 G, 최소공배수를 L => AB=LG
- 최대 공약수 알면,
AB / G = L
소인수 분해

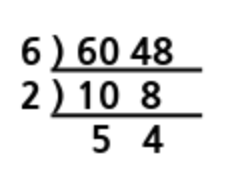
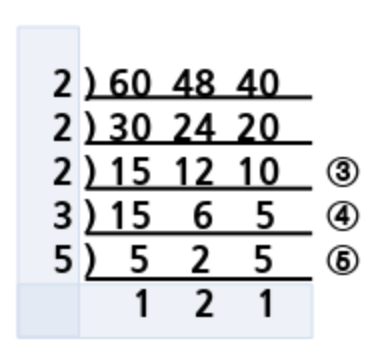
유클리드 호제법
- https://dimenchoi.tistory.com/46
- A를 B로 나눈 몫을 Q라 하고, 나머지를 R이라 하자. 이 때, gcd(A,B)=gcd(B,R)
- A와 B의 최대공약수를 구하기 위해서 A를 B로 나눈 나머지 R1을 구합니다.
- B를 R1으로 나눈 나머지 R2를 구합니다.
- R1을 R2로 나눈 나머지 R3를 구합니다.
- 이 과정을 계속 반복하여, 어느 한 쪽이 나누어떨어질 때까지 반복합니다.
- 이 직전 얻은 나머지가 최대공약수입니다.
등차 등비 수열



- 이때,
a != 0, r != 0이다. - 꼭 첫째 항이 아니더라도, 하나 이상의 항의 값, 몇 번째 항인지, 그리고 공비가 주어지거나 둘 이상의 항의 값, 각각 몇 번째 항인지가 주어지면 등비수열의 일반항을 정할 수 있다.
순열과 조합
https://ourcstory.tistory.com/414
items = ['1', '2', '3', '4', '5']
from itertools import permutations
list(permutations(items, 2))
# [('1', '2'), ('1', '3'), ('1', '4'), ('1', '5'), ('2', '1'), ('2', '3'), ('2', '4'), ('2', '5'), ('3', '1'), ('3', '2'), ('3', '4'), ('3', '5'), ('4', '1'), ('4', '2'), ('4', '3'), ('4', '5'), ('5', '1'), ('5', '2'), ('5', '3'), ('5', '4')]
from itertools import combinations
list(combinations(items, 2))
# [('1', '2'), ('1', '3'), ('1', '4'), ('1', '5'), ('2', '3'), ('2', '4'), ('2', '5'), ('3', '4'), ('3', '5'), ('4', '5')]
# 두 개 이상의 리스트에서 모든 조합
from itertools import product
items = [['a', 'b', 'c,'], ['1', '2', '3', '4'], ['!', '@', '#']]
list(product(*items))
# [('a', '1', '!'), ('a', '1', '@'), ('a', '1', '#'), ('a', '2', '!'), ('a', '2', '@'), ('a', '2', '#'), ('a', '3', '!'), ('a', '3', '@'), ('a', '3', '#'), ('a', '4', '!'), ('a', '4', '@'), ('a', '4', '#'), ('b', '1', '!'), ('b', '1', '@'), ('b', '1', '#'), ('b', '2', '!'), ('b', '2', '@'), ('b', '2', '#'), ('b', '3', '!'), ('b', '3', '@'), ('b', '3', '#'), ('b', '4', '!'), ('b', '4', '@'), ('b', '4', '#'), ('c,', '1', '!'), ('c,', '1', '@'), ('c,', '1', '#'), ('c,', '2', '!'), ('c,', '2', '@'), ('c,', '2', '#'), ('c,', '3', '!'), ('c,', '3', '@'), ('c,', '3', '#'), ('c,', '4', '!'), ('c,', '4', '@'), ('c,', '4', '#')]- (위에 이어서) 곱집합(Cartesian product) 구하기 - product
import itertools
iterable1 = 'ABCD'
iterable2 = 'xy'
iterable3 = '1234'
print(list(itertools.product(iterable1, iterable2, iterable3)))피보나치 DP
def solution(n):
answer = 0
dp = [0]*100_001
dp[0] = 0
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 2] + dp[i - 1]
return dp[n] % 12345671로 만들기 DP
# 5로 나누어지면 /5
# 3으로 나누어지면 /3
# 2로 나우어지면 /2
# X = X -1
# 1로 만드는 최소 연산 수
# 답 = min(/5, /3, /2, -1) + 1 (각 경우의 수 의미)
def solution(n):
d = [0] * 30_001
for i in range(2, n + 1):
d[i] = d[i - 1] + 1
if i % 2 == 0:
d[i] = min(d[i], d[i // 2] + 1)
if i % 3 == 0:
d[i] = min(d[i], d[i // 3] + 1)
if i % 5 == 0:
d[i] = min(d[i], d[i // 5] + 1)
return d[n]2거듭 제곱과 비트 연산
-
특정 값 x를 log(n, 2)를 취하면 2의 거듭제곱인 것을 알 수 있다. 하지만 math.log() 함수는 부동소수점 계산을 수행
-
비트연산의 특이점을 활용한다. 2의 거듭제곱인 숫자는 이진수로 표현했을 때 한 비트만이 1이고, 나머지 비트는 모두 0인 패턴을 가진다.
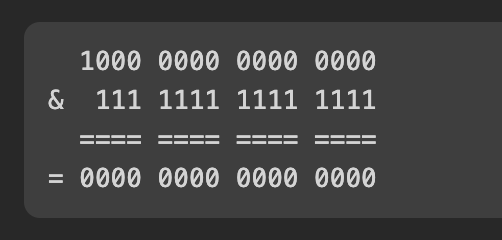
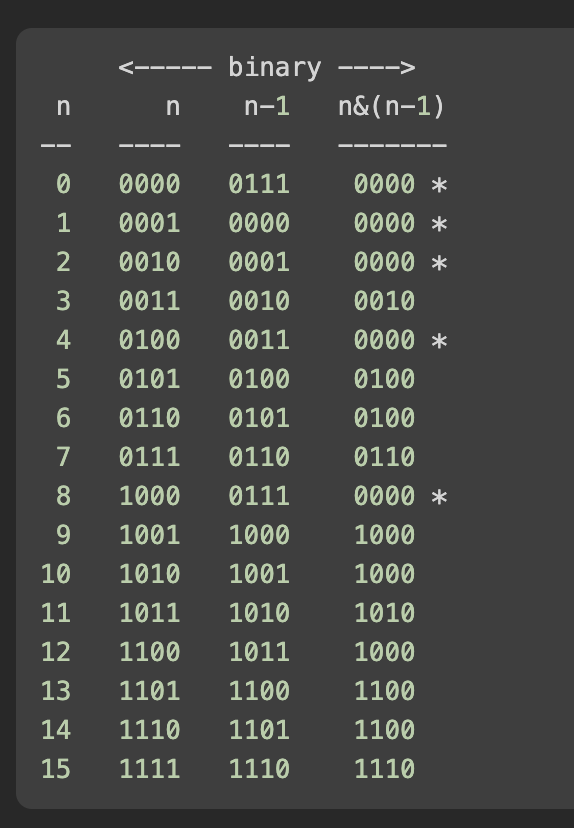
class Solution:
def isPowerOfTwo(self, n: int) -> bool:
return n>0 and n&(n-1)==0digital root
-
음이 아닌 정수의 자릿수근(영어: digital root, 반복적 자릿수합(repeated digital sum)이라고도 함)은 자릿수를 더하는 과정을 방금 구한 그 값의 자릿수합에서 자릿수합을 구하도록 반복해서 얻어지는 (한 자리) 값이다. 이 과정은 한 자리 수가 될 때까지 계속된다.
-
예를 들어, 65,536의 자릿수근은 7이다. 왜냐하면 6 + 5 + 5 + 3 + 6 = 25이고 2 + 5 = 7이기 때문이다.
-
"어떤 수가 9의 배수라면, 그 수의 모든 자릿수의 합도 9의 배수" 라는 규칙을 통해 자릿수근을 쉽게 구할 수 있다.
class Solution(object):
def addDigits(self, num):
if num == 0:
return 0
return num % 9 or 94) 그래프
기본 개념과 구현
-
그래프는 정점(Vertex, 또는 노드(Node)라고도 함) 과 이들을 연결하는 간선(Edge)으로 구성된 자료구조
-
방향성이 있는 방향 그래프(Directed Graph) 와 방향성이 없는 무방향 그래프(Undirected Graph)로 나뉘며, 간선에 가중치(Weight) 가 있을 수도 있다.
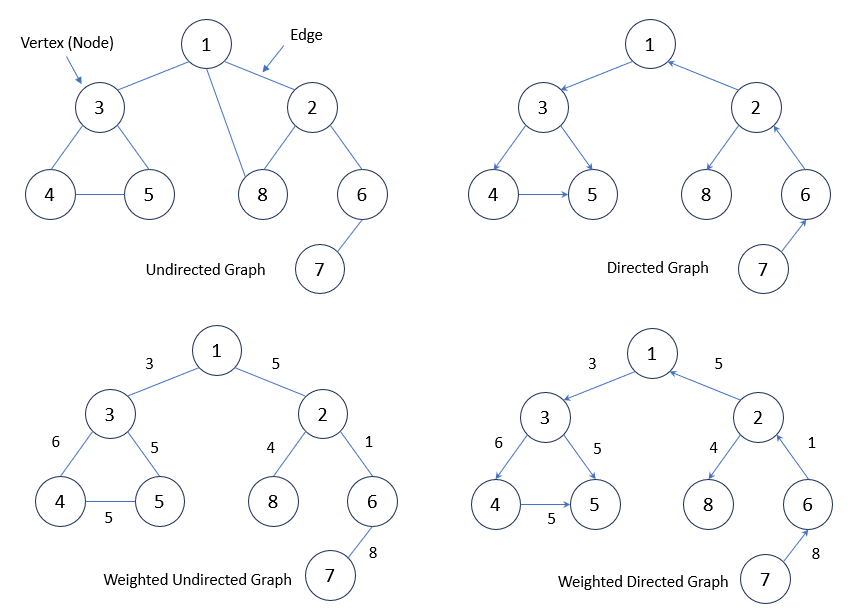
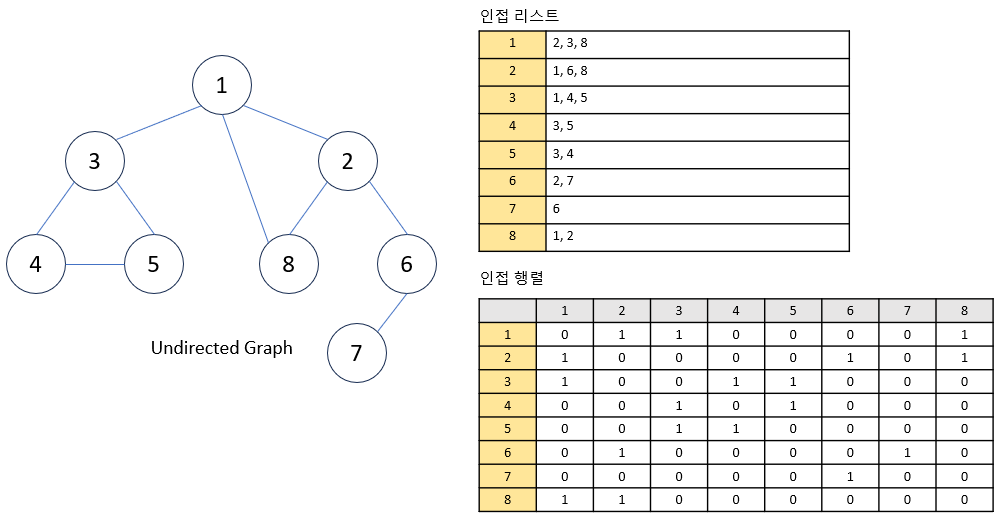
- 그래프를 구현하는 방법으로는 인접 리스트(Adjacency List) 와 인접 행렬(Adjacency Matrix) 을 사용하는 방법이 있다.
-
[인접 리스트] 는 각 정점에 대해 연결된 모든 정점의 리스트를 저장하는 방식 으로, 특정 정점과 인접한 정점들을 바로 알 수 있다는 장점
-
[인접 행렬] 은 2차원 배열을 사용하여 노드 간의 연결 관계를 행렬 형태로 나타내는 방식.
-
노드 간의 연결 여부를 빠르게 확인할 수 있다는 장점이 있지만, 모든 각 정점에 관한 관계를 기록하기 때문에 메모리 소비가 더 크다는 단점이 있다.
-
따라서 인접 행렬은 그래프 간선이 많은 그래프에 주로 사용하고, 인접 리스트는 상대적으로 간선이 적은 그래프에서 주로 사용
DFS, BFS
- 얘들도 기본형태는 "완전탐색" 인 것을 잊지말자
- 보통 배열형태의 "길 찾기", "길 따라가기", "경우의 수" 계산 느낌이다.
from collections import deque
graph = dict(
A=['B', 'C'],
B=['A', 'D'],
C=['A', 'G', 'H', 'I'],
D=['B', 'E', 'F'],
E=['D'],
F=['D'],
G=['C'],
H=['C'],
I=['C', 'J'],
J=['I']
)
def bfs(graph, node, visited=[]):
'''
- deque를 활용한 bfs
'''
# 큐 구현을 위한 deque 라이브러리 활용
queue = deque([node])
if not visited:
visited = [False] * (len(graph) + 1)
visited[node] = True # 현재 노드를 방문 처리
# 큐가 완전히 빌 때까지 반복
while queue:
v = queue.popleft() # 큐에 삽입된 순서대로 노드 하나 꺼내기
sys.stdout.write(str(v)) # 탐색 순서 출력
# 인접한 행렬 체크 여부, 구현하기에 따라 달라짐
if isinstance(graph[v], int):
continue
# 현재 처리 중인 노드에서 방문하지 않은 인접 노드를 모두 큐에 삽입
for i in graph[v]:
if not (visited[i]):
queue.append(i)
visited[i] = True
def dfs_deque(graph, start_node):
'''
- deque 활용한 stack, DFS
'''
visited = []
need_visited = deque()
# 시작 노드 설정해주기
need_visited.append(start_node)
# 방문이 필요한 리스트가 아직 존재한다면
while need_visited:
# 시작 노드를 지정하고
node = need_visited.pop()
# 만약 방문한 리스트에 없다면
if node not in visited:
# 방문 리스트에 노드를 추가
visited.append(node)
# 인접 노드들을 방문 예정 리스트에 추가
need_visited.extend(graph[node])
return visited
def dfs_recursive(graph, start, visited=[]):
'''
- 재귀를 활용한 dfs
'''
sys.stdout.write(str(start))
visited.append(start)
# 인접한 행렬 체크 여부, 구현하기에 따라 달라짐
if isinstance(graph[start], int):
return visited
for node in graph[start]:
if node not in visited:
dfs_recursive(graph, node, visited)
return visited- python으로 기깔나게 DFS simple 순회 숏코드가 가능하다.
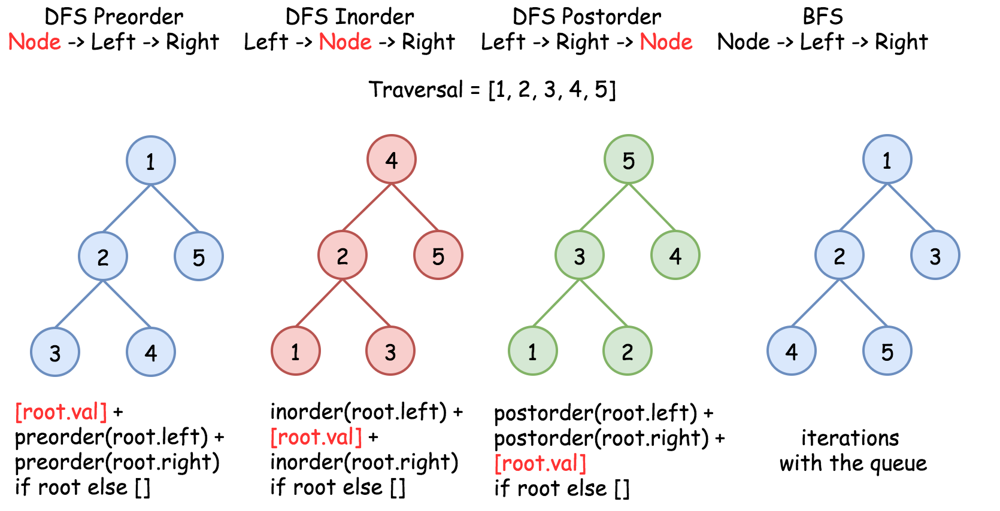
def preorder(root):
return [root.val] + preorder(root.left) + preorder(root.right) if root else []
def inorder(root):
return inorder(root.left) + [root.val] + inorder(root.right) if root else []
def postorder(root):
return postorder(root.left) + postorder(root.right) + [root.val] if root else []Binary Search / 이진 탐색
- 정렬이 되어 있어야 하고, 분할 탐색 형태, 데이터를 나누어서 접근하는 반복-높이가 logN
- 단순 반복문 (while)을 통해 구현하는게 편할 수 있지만, 제귀가 더 단순해진다.
def binary_search(arr, target, low=None, high=None):
low, high = low or 0, high or len(arr) - 1
if low > high:
return -1
mid = (low + high) // 2
if arr[mid] > target:
return binary_search(arr, target, low, mid)
if arr[mid] == target:
return mid
if arr[mid] < target:
return binary_search(arr, target, mid + 1, high)BST
class Node:
def __init__(self, value: int):
self.value = value
self.left: Node = None # 왼쪽 서브노드
self.right: Node = None # 오른쪽 서브노드
class BinarySearchTree:
def __init__(self, root: Node):
self.root = root # root node
def insert_node(self, value):
'''
- 왼쪽 자식 노드 값 < 부모 노드 값 < 오른쪽 자식 노드 값 규칙을 지키면서 append (추가) 하는 method
'''
curr: Node = self.root # 연산의 기준 노드 변수 선언
while True:
# 기준 노드 값이 삽입하고자 하는 값보다 큰 경우 (삽입 값은 좌측 노드로 내려간다)
if curr.value > value:
if curr.left: # 기준 노드의 좌측 자식노드가 존재한다면
curr = curr.left # 다음 연산을 위해 기준노드를 좌측 자식노드로 초기화
else: # 기준 노드의 좌측 자식노드가 존재하지 않는다면
curr.left = Node(value) # 좌측 자식노드에 값 삽입
break
# 기준 노드 값이 삽입하고자 하는 값보다 작은 경우
else:
if curr.right: # 기준 노드의 우측 자식노드가 존재한다면
curr = curr.right # 다음 연산을 위해 기준노드를 우측 자식노드로 초기화
else: # 기준 노드의 우측 자식노드가 존재하지 않는다면
curr.right = Node(value) # 우측 자식노드에 값 삽입
break
def search_node(self, value):
'''
- BST의 특성을 생각하면서 탐색하는 method
'''
curr = self.root # 연산의 기준 노드 변수 선언
while curr: # 기준 노드가 존재하는 동안
if curr.value == value: # 기준 노드의 값이 검색하고자 하는 값과 같다면
return True # True 반환
break
elif curr.value > value: # 기준 노드의 값이 검색하고자 하는 값보다 클 때
if curr.left: # 기준 노드의 좌측 자식노드가 존재한다면
curr = curr.left # 다음 연산을 위해 기준 노드를 좌측 자식노드로 초기화
else: # 기준 노드의 좌측 자식노드가 없다면
return False # False 반환(검색하고자 하는 값이 없음)
elif curr.value < value: # 기준 노드의 값이 검색하고자 하는 값보다 작을 때
if curr.right: # 기준 노드의 우측 자식노드가 존재한다면
curr = curr.right # 다음 연산을 위해 기준 노드를 우측 자식노드로 초기화
else: # 기준 노드의 우측 자식노드가 없다면
return False # False 반환(검색하고자 하는 값이 없음)
def debugPrint(self, start: Node, level: int) -> None:
'''
- 깊이 우선 탐색의 특성으로 그래프 출력하기
'''
print(f'Node: {start.value}, childs:')
for node in [start.left, start.right]:
if not node:
continue
print(' ' * level, end='')
self.debugPrint(node, level+1)LIS / LCS - DP
-
LIS 는 수열에서 항상 증가하는 부분 수열 중 가장 긴 길이를 구하는 문제로, 보통 DP로
O(N²), 이분 탐색으로O(NlogN)에 해결한다. -
LCS 는 두 문자열에서 순서를 유지하면서 공통으로 등장하는 가장 긴 부분 수열의 길이를 구하는 문제이며, 2차원 DP로 접근한다.
def LIS(arr):
dp = [1] * len(arr)
for i in range(len(arr)):
for j in range(i):
if arr[j] < arr[i]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
print(LIS([10, 20, 10, 30, 20, 50])) # 출력: 4def LCS(s1, s2):
dp = [[0]*(len(s2)+1) for _ in range(len(s1)+1)]
for i in range(1, len(s1)+1):
for j in range(1, len(s2)+1):
if s1[i-1] == s2[j-1]:
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
print(LCS("ACAYKP", "CAPCAK")) # 출력: 4Dijkstra / Floyd-Warshall
- 그래프에서 한 정점에서 모든 다른 정점까지의 최단 경로를 구하는 알고리즘으로, 그리디 + 우선순위 큐를 활용해 구현된다.
import heapq
def dijkstra(start, graph):
distance = [float('inf')] * len(graph)
distance[start] = 0
hq = [(0, start)]
while hq:
dist, now = heapq.heappop(hq)
if distance[now] < dist:
continue
for next_node, weight in graph[now]:
cost = dist + weight
if cost < distance[next_node]:
distance[next_node] = cost
heapq.heappush(hq, (cost, next_node))
return distance
graph = [
[], # 0번 노드 없음
[(2, 2), (3, 5), (4, 1)],
[(3, 3), (4, 2)],
[(2, 3), (6, 5)],
[(3, 3), (5, 1)],
[(3, 1), (6, 2)],
[]
]
print(dijkstra(1, graph)) # 1번 노드에서 시작하는 최단거리- 플로이드워셜, 모든 노드 간 최단거리, 모든 정점 간의 최단 거리를 구하는 알고리즘으로, DP를 기반으로 하고 3중 for문을 사용한다.
INF = int(1e9)
def floyd_warshall(n, graph):
for k in range(n):
for i in range(n):
for j in range(n):
graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
return graph
n = 4
graph = [
[0, 5, INF, 8],
[INF, 0, INF, 2],
[INF, 3, 0, INF],
[INF, INF, 1, 0]
]
result = floyd_warshall(n, graph)
for row in result:
print(row)Topological Sort
- 사이클이 없는 방향 그래프에서 작업 순서나 선후 관계를 정하는 데 사용하는 알고리즘으로, 큐 기반 탐색으로 구현한다.
from collections import deque
def topological_sort(n, graph, indegree):
result = []
q = deque([i for i in range(1, n+1) if indegree[i] == 0])
while q:
now = q.popleft()
result.append(now)
for next_node in graph[now]:
indegree[next_node] -= 1
if indegree[next_node] == 0:
q.append(next_node)
return result
n = 6
graph = [[] for _ in range(n+1)]
indegree = [0]*(n+1)
edges = [(1,5),(1,4),(2,4),(3,5),(4,6),(5,6)]
for a, b in edges:
graph[a].append(b)
indegree[b] += 1
print(topological_sort(n, graph, indegree)) # 출력: [1, 2, 3, 4, 5, 6]Union-Find
- 서로소 집합: 공통 원소가 없는 두 집합
- 서로소 집합을 관리하며 두 원소가 같은 집합에 속하는지 확인하고, 합치는 연산을 빠르게 처리할 수 있는 자료구조이다.
def find(parent, x):
if parent[x] != x:
parent[x] = find(parent, parent[x])
return parent[x]
def union(parent, a, b):
a = find(parent, a)
b = find(parent, b)
if a < b:
parent[b] = a
else:
parent[a] = b
parent = [i for i in range(6)] # 0~5
union(parent, 1, 4)
union(parent, 2, 3)
union(parent, 2, 4)
for i in range(1, 6):
print(f"{i}번 노드의 루트: {find(parent, i)}")MST(Minimum Spanning Tree)
- 그래프에서 모든 정점을 연결하면서 간선의 가중치 합이 최소가 되는 트리를 찾는 문제로,
Kruskal또는Prim알고리즘을 사용한다.
def find(parent, x):
if parent[x] != x:
parent[x] = find(parent, parent[x])
return parent[x]
def union(parent, a, b):
a, b = find(parent, a), find(parent, b)
if a != b:
parent[b] = a
edges = [(1, 2, 1), (1, 3, 2), (2, 3, 2), (2, 4, 3), (3, 4, 1)]
edges.sort(key=lambda x: x[2]) # 비용 기준 정렬
parent = [i for i in range(5)] # 0~4
total_cost = 0
for a, b, cost in edges:
if find(parent, a) != find(parent, b):
union(parent, a, b)
total_cost += cost
print("MST total cost:", total_cost)3. 참고하면 좋은 링크 모음
1) 20 of these coding problem patterns (leetcode 기준)
- Sliding Window
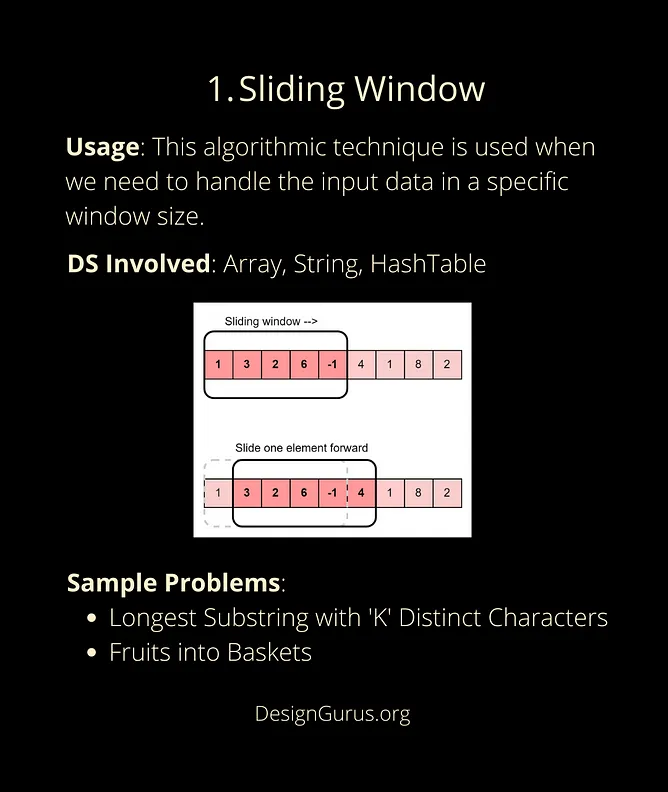
- Islands (Matrix Traversal)

- Two Pointers

- Fast & Slow Pointers

- Merge Intervals
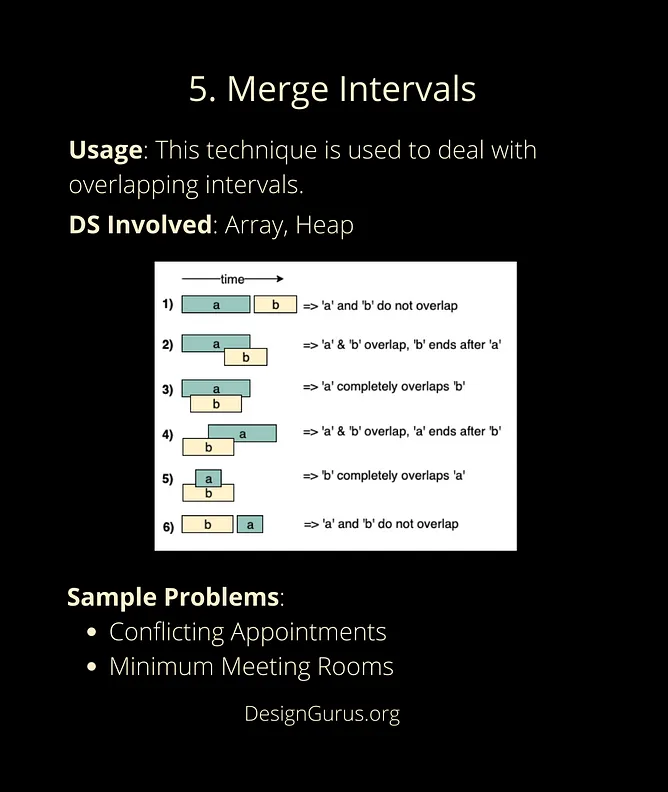
- Cyclic Sort

- In-place Reversal of a LinkedList

- Tree Breadth-First Search

- Tree Depth First Search

- Two Heaps

- Subsets

- Modified Binary Search

- Bitwise XOR

- Top ‘K’ Elements

- K-way Merge

- Topological Sort

- 0/1 Knapsack

- Fibonacci Numbers

- Palindromic Subsequence

- Longest Common Substring
