이번 시간엔 AVL 트리에 대해서 알아보자.
균형 이진 탐색 트리 (Balanced BST)
-
이진 탐색 트리에서 탐색(Search), 삽입(Insert),
삭제(Delete) 등의 연산은 트리의 높이 ℎ에 비례하
는 시간 즉, 𝑂(ℎ) 시간이 소요된다. -
이진 탐색 트리의 높이를 𝑂(log 𝑛)으로 제한할 수
있으면, 위의 연산 모두 𝑂(log 𝑛) 시간에 수행된다. -
높이가 𝑂(log 𝑛)인 이진 탐색 트리를 균형 이진 탐
색 트리라고 한다. -
균형 이진 탐색 트리에는 AVL 트리, 레드-블랙 트
리 등이 있다.
AVL 트리(Tree) 개념 및 구현
- AVL 트리는 스스로 균형을 잡는 이진 탐색 트리다.
-
트리의 높이가 h일 때 이진 탐색 트리의 시간 복잡도는 O(h)다.
-
한쪽으로 치우친 편향 이진트리가 되면 트리의 높이가 높아지기 때문에 이를 방지하고자 높이 균형을 유지하는 AVL 트리를 사용하게 된다.
AVL트리는 다음과 같은 특징을 가진다.
-
AVL 트리는 이진 탐색 트리의 속성을 가집니다.
-
왼쪽, 오른쪽 서브 트리의 높이 차이가 최대 1 입니다.
어떤 시점에서 높이 차이가 1보다 커지면 회전(rotation)을 통해 균형을 잡아 높이 차이를 줄입니다. -
AVL 트리는 높이를 logN으로 유지하기 때문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN) 입니다.
Balance Factor(BF)
Balance Factor(BF)는 외쪽 서브트리의 높이에서 오른쪽 서브트리의 높이를 뺀 값입니다.
Balance Factor (k) = height (left(k)) - height(right(k))
-
BF가 1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 높다는 것을 의미합니다.
-
BF가 0이면 왼쪽 서브트리와 오른쪽 서브트리의 높이가 같다는 것을 의미합니다.
-
BF가 -1이면 왼쪽 서브트리가 오른쪽 서브트리보다 높이가 한단계 낮다는 것을 의미합니다.
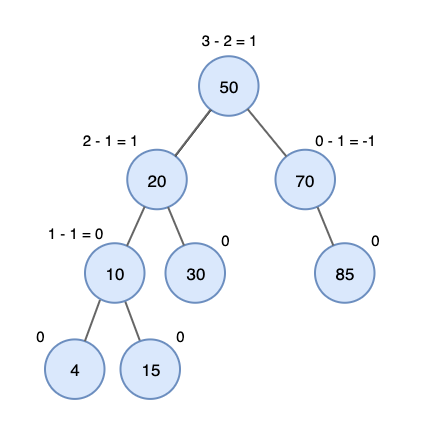
다음은 ALV 트리의 예입니다. BF가 -1과 +1 사이에 있음을 알 수 있습니다.
Q. 𝑛개의 노드를 가진 AVL 트리의 최대 높이는?
높이 ℎ인 AVL 트리의 최소 노드 개수 𝑛ℎ를 구한다.
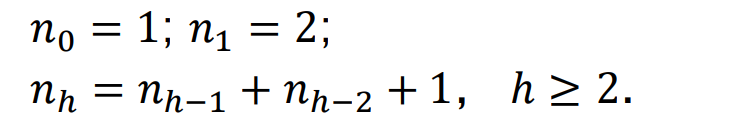
위 점화식을 풀면 다음과 같다. 증명해 보시오.
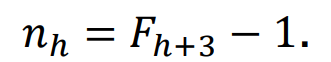

따라서 AVL 트리의 높이는 𝑂(log 𝑛)이다
시간 복잡도 (Time complexity)
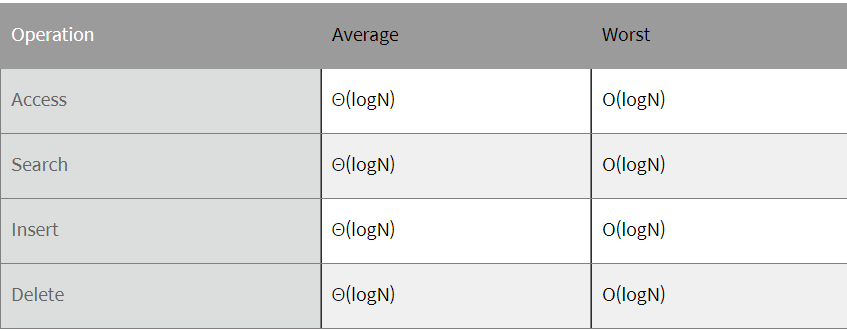
N은 트리의 노드 수입니다.
AVL 트리는 높이를 logN으로 유지하기 때문에 삽입, 검색, 삭제의 시간 복잡도는 O(logN)입니다.
회전 (rotation)
-
AVL 트리에서 이진 탐색 트리의 삽입 알고리즘을 이용하여 노드를 삽입하면 균형 인자가 2 혹은 -2 가 되는 노드가 생길 수 있다.
-
이 경우 AVL 트리를 유지하도록 보정 작업이 필요 한데, LL, LR, RL, RR 등 네 종류의 회전이 있다
LL(Left Left) case
y는 z의 왼쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우 right rotation을 수행하여 균형을 맞춥니다.
right rotation 수행 과정
- y노드의 오른쪽 자식 노드를 z노드로 변경합니다.
- z노드 왼쪽 자식 노드를 y노드 오른쪽 서브트리(T2)로 변경합니다.
- y는 새로운 루트 노드가 됩니다.

Right rotation 코드 구현
struct node *rightRotate (struct node *z) {
struct node *y = z->left;
struct node *T2 = y->right;
// y의 오른쪽 자식 노드를 z로 지정
y->right = z;
// z의 왼쪽 자식 노드를 T2로 지정
z->left = T2;
// 새로운 루트 노드 y를 반환
return y;
}RR(Right Right) case
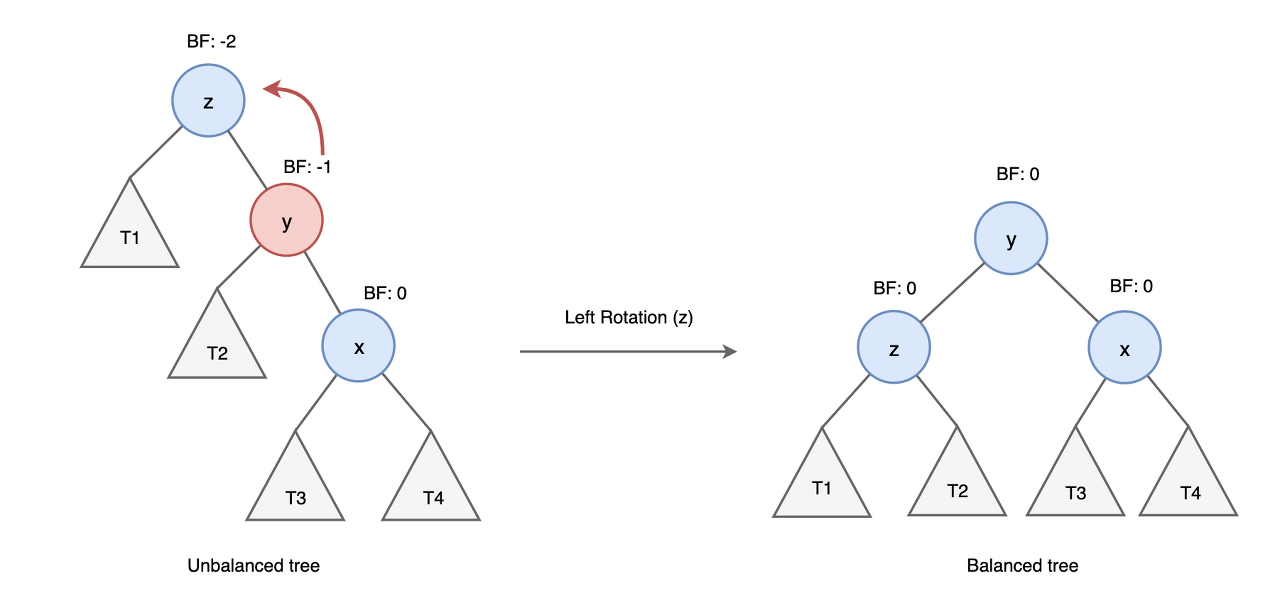
y는 z의 오른쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left rotation을 수행하여 균형을 맞춥니다.
left rotation 수행 과정
- y노드의 왼쪽 자식 노드를 z노드로 변경합니다.
- z노드 오른쪽 자식 노드를 y노드 왼쪽 서브트리(T2)로 변경합니다.
- y는 새로운 루트 노드가 됩니다.
left rotation 코드구현
struct node *lefttRotate (struct node *z) {
struct node *y = z->right;
struct node *T2 = y->left;
// y의 왼쪽 자식 노드를 z로 지정
y->left = z;
// z의 오른쪽 자식 노드를 T2로 지정
z->right = T2;
// 새로운 루트 노드 y를 반환
return y;
}LR(Left Right) case
y는 z의 왼쪽 자식 노드이고, x는 y의 오른쪽 자식 노드인 경우 left , right 순으로 총 두 번의 rotation을 수행하여 균형을 맞춘다.
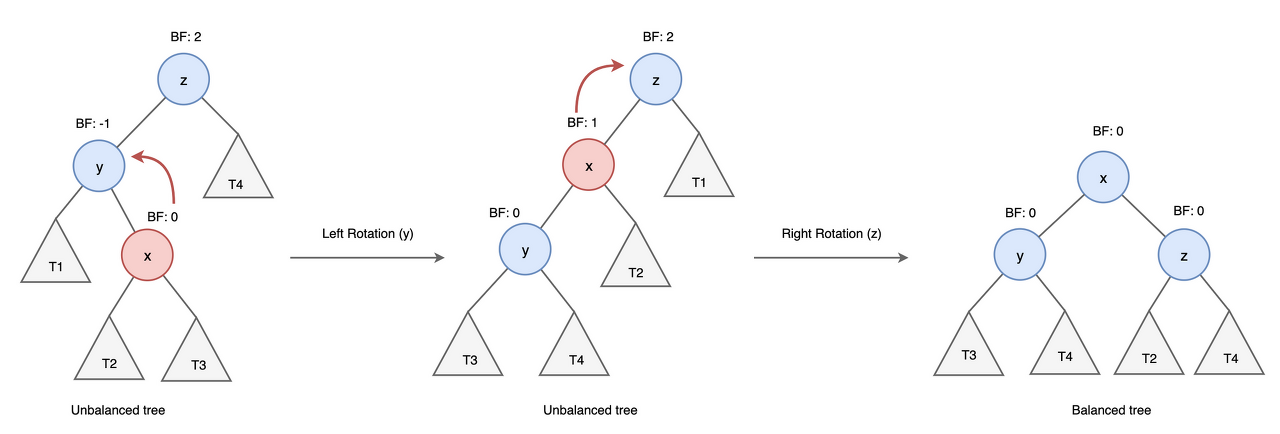
코드 구현
y = z->left;
y = leftRotate(y);
z = rightRotate(z);RL(Right Left) case
y는 z의 오른쪽 자식 노드이고, x는 y의 왼쪽 자식 노드인 경우, right, left 순으로 총 두번의 rotation을 수행하여 균형을 맞춘다.
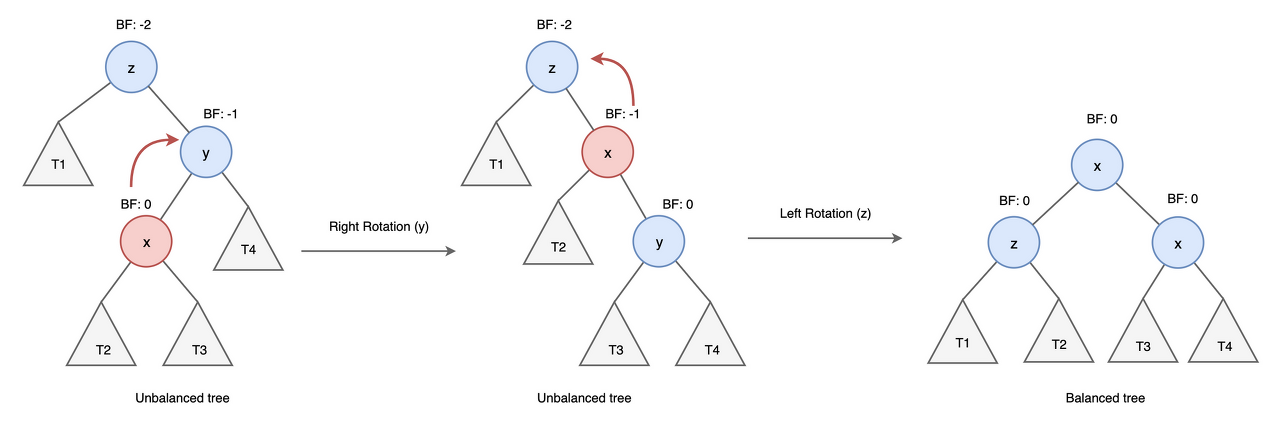
<RL 코드 구현>
y = z->right;
y = rightRotate(y);
z = leftRotate(z);코드
struct node {
int key;
struct node *left, *right;
int height;
};
int max(int a, int b) {
return (a > b)? a : b;
}
struct node* newNode(int key) {
struct node *temp = (struct *node)malloc(sizeof(struct node));
temp->data = key;
temp->left = NULL;
temp->right = NULL;
temp->height = 1;
return temp;
}
struct node *lefttRotate (struct node *z) {
struct node *y = z->right;
struct node *T2 = y->left;
// left 회전 수행
y->left = z;
z->right = T2;
// 노드 높이 갱신
z->height = 1 + max(z->left->height, z->right->height);
y->height = 1 + max(y->left->height, y->right->height);
// 새로운 루트 노드 y를 반환
return y;
}
struct node *rightRotate (struct node *z) {
struct node *y = z->left;
struct node *T2 = y->right;
// right 회전 수행
y->right = z;
z->left = T2;
// 노드 높이 갱신
z->height = 1 + max(z->left->height, z->right->height);
y->height = 1 + max(y->left->height, y->right->height);
// 새로운 루트 노드 y를 반환
return y;
}
// BF(BalanceFactor)값을 가져오는 함수.
int getBalanceFactor(struct node *n) {
if (n == NULL)
return 0;
return n->left->height - n->right->height;
}
// 트리의 높이 균형을 유지하는 함수.
// 4가지 케이스를 가지고 rotate를 수행함.
struct node* rebalance(struct node* root) {
int bFactor = getBalanceFactor(root);
// LL Case
if (bFactor > 1 && key < node->left->key)
return rightRotate(root);
// RR Case
if (bFactor < -1 && key > node->right->key)
return leftRotate(root);
// LR Case
if (bFactor > 1 && key > node->left->key){
root->left = leftRotate(root->left);
return rightRotate(root);
}
// RL Case
if (bFactor < -1 && key < node->right->key){
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// 삽입 함수.
struct node* insert(struct node* root, int key) {
// 삽입 수행
if (root == NULL)
return newNode(key);
if (key > root->data)
root->right = insert(root->right, key);
else if (key < root->data)
root->left = insert(root->left, key);
else
return root;
// 노드 높이 갱신
root->height = 1 + max(node->left->height, node->right->height);
// 노드 균형 유지
root = rebalance(root);
return root;
}