이번 시간에는 BFS(너비 우선 탐색)에 대한 내용이다.

BFS(Breadth First Search, 너비 우선 탐색)
DFS는 스택 자료구조를 활용해 구현했다면, BFS는 Queue를 활용한다.

DFS는 갈 수 있는 곳까지 들어가서 확인하고, 갈 곳이 없으면 다시 되돌아와 다른 길을 찾는 식이다. 이를 깊이 우선 탐색이라고 부른다.

BFS는 시작점의 인접한 정점들을 차례로 모두 방문하고, 방문했던 정점을 시작점으로 해서 다시 인접한 정점들을 차례로 모두 방문하고 하는 방식으로, 너비 우선 탐색이라고 부른다.

왜 BFS를 사용하는가?

너비 우선 탐색의 사용 목적은 시작 정점부터 다른 정점까지의 최단 거리를 구하기 위해 사용한다.

너비 우선 탐색과 많이 비교되는 깊이 우선 탐색은 최대한 깊게 가는 것을 목적으로 구현되기 때문에 값이 존재하는지 확인하기 위해 사용되지만 너비 우선 탐색은 시작 정점을 기준으로 원(?)처럼 퍼져나가기 때문에 목표 지점을 처음 방문하게 되면 가장 짧게 방문하는 케이스가 된다.

이런 이유로 최단 거리를 구할 때 보통 깊이 우선 탐색보다는 너비 우선 탐색을 많이 사용한다

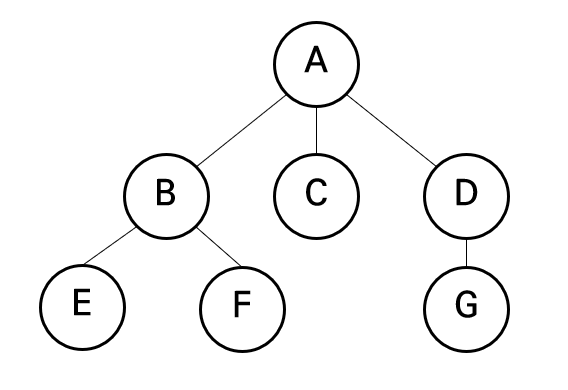
위 그림에서 BFS(너비 우선 탐색)을 진행한다면, 시작점을 A라고 하였을 때 A-B-C-D-E-F 순으로 탐색하게 됩니다

BFS 알고리즘

• 한편 BFS 알고리즘은 큐(Queue)라는 자료구조를 이용해서 어디를 방문할 것인지를 기록합니다. 탐색 진행 방식은 다음과 같습니다.

• BFS에서는 갈 수 있는 모든 정점을 일단 Queue에 넣는다. Queue에 넣는 행위는 '방문했다'라는 것을 의미한다.

• 방문했다는 것을 의미하는 check[i]를 변경하는 시점은 queue에 넣을 정점을 때다.

• queue에 넣어놓고 check[i]를 변경시키지 않으면 방문한 정점이 queue에 중복되어 생기기 때문이다. 이는 모든 정점을 한 번씩 방문하겠다는 그래프의 탐색 목적에 위배된다.

• queue가 비어있으면 BFS 탐색을 완료한다

BFS의 탐색 과정

[1] 처음 시작 노드 방문 (A)

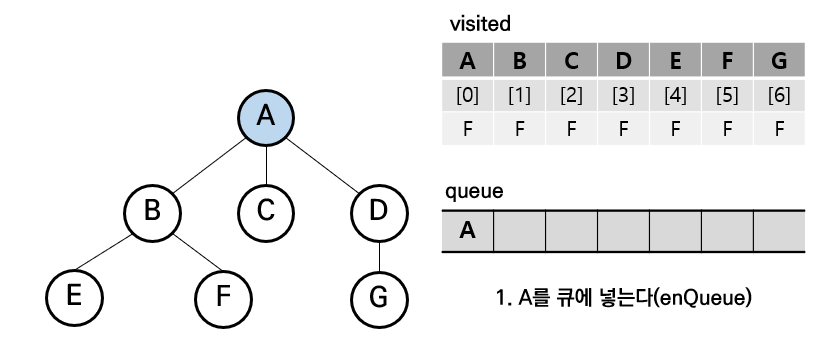
[2] A는 큐에서 삭제 및 방문 표시 후 A의 인접 노드들을 큐에 삽입

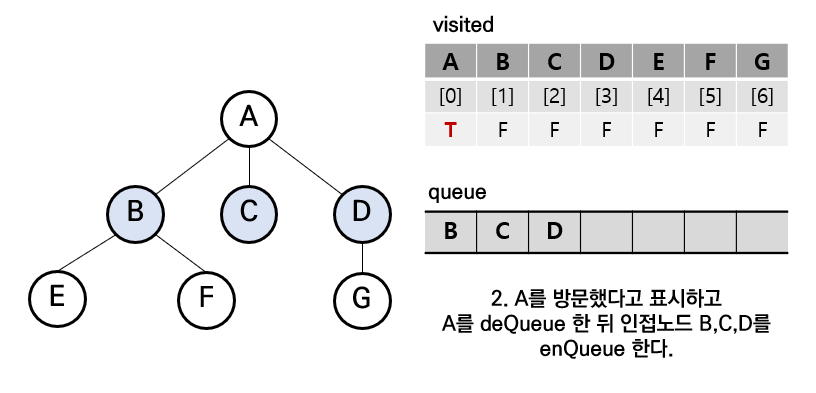
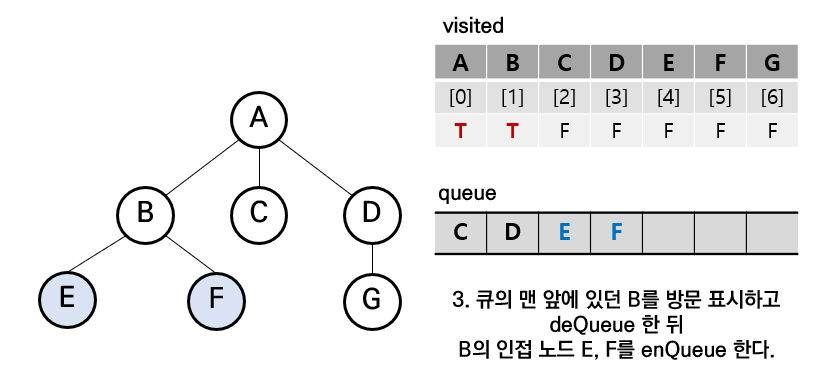
[3] A의 인접노드들 중 가장 큐에 먼저 들어간 B를 큐에서 삭제 및 방문 표시, B의 인접 노드들을 큐에 삽입

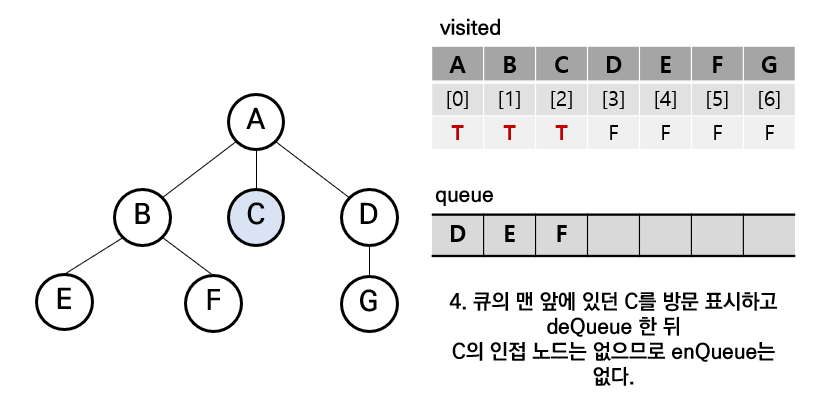
[4] C를 큐에서 삭제 및 방문 표시, C의 인접 노드를 큐에 넣으려 했으나 없으므로 skip

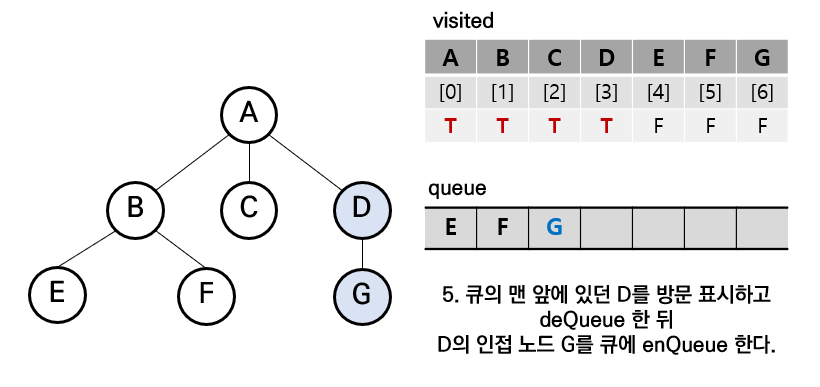
[5] 마찬가지로 D도 큐에서 삭제 및 방문 표시, D의 인접 노드 G를 큐에 삽입

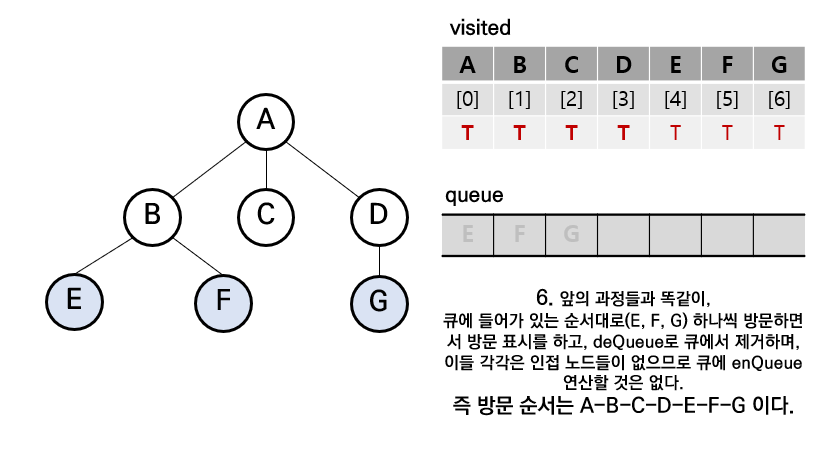
[6] 큐에 남아있는 요소들을 차례대로 위와 같은 방법으로 방문 및 표시하면서 결과적으로 BFS 탐색 완료(큐가 완전히 비게 될 때)

※ BFS를 직접 코드상에서 구현할 때에는 deQueue 연산으로 큐의 맨 앞에 있는 것이 무엇인지 알아내는 것이므로, 큐에서 먼저 빼낸 후(deQueue) 그와 동시에 그 노드의 방문 표시를 할 수 있게끔 한다.

<코드>

void BFS(int v)
{
	node_pointer w;

	initialize Queue;
	printf("%d", v);
	visited[v] = TRUE;
	enqueue(v);
	while (!empty(Queue))
	{
		v = dequeue();
		for (w = graph[v]; w; w = w->link)
		{
			if (!visited[w->vertex])
			{
				printf("%d", w->vertex);
				visited[w->vertex] = TURE;
				enqueue(w->vertex);
			}
		}
	}

}

BFS 시간복잡도

인접행렬을 통한 구현

• 시간복잡도 : 모든 정점을 방문해야 하므로 while문이 V번 반복되는데
  내부의 for문에 의해서 각각은 O(V)의 시간복잡도를 가지므로
  전체를 모두 1번씩 탐색하는 경우 V x O(V) = O(V^2)의 시간복잡도를 가진다.

인접리스트를 통한 구현

• 시간복잡도 : 모든 정점을 방문해야 하므로 while문이 V번 반복되는데
  내부의 for문에 의해서 각각은 다른 횟수의 반복을 하게되는데 이를 모두 합하면 E번이 된다.
  따라서, 전체를 모두 1번씩 탐색하는 경우 O(V + E)의 시간복잡도를 가진다.

연결성분(마지막)

마지막 그래프의 연결성분은 DFS나 BFS를 이용하여 찾을 수 있다.

• 방문하지 않은 정점이 남아 있다면, 임의의 방문되지 않은 정점에서 DFS(혹은 BFS)를 실행한다.

• 위 과정을 반복한다.

  코드

void connected(void)
{
	int k ;
    
    for(k = 0; k < n; k++)
    {
    	if(!visited[k])
        	DFS(K);
            printf("\n");
    }

}

출처

https://chanhuiseok.github.io/posts/algo-27/
https://ldgeao99.tistory.com/386