그래프 탐색 및 순회 중에서 깊이 우선 탐색에 대해 알아보자.

DFS 장/단점

장점

1. 현 경로상의 노드들만 기억하면 되므로 저장공간 수요가 비교적 적다.
2. 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.

단점

1. 해가 없는 경로가 깊을 경우 탐색시간이 오래 걸릴 수 있다.
2. 얻어진 해가 최단 경로가 된다는 보장이 없다.
3. 깊이가 무한히 깊어지면 스택오버플로우가 날 위험이 있다.(이것은 깊이 제한을 두는 방법으로 해결 가능)

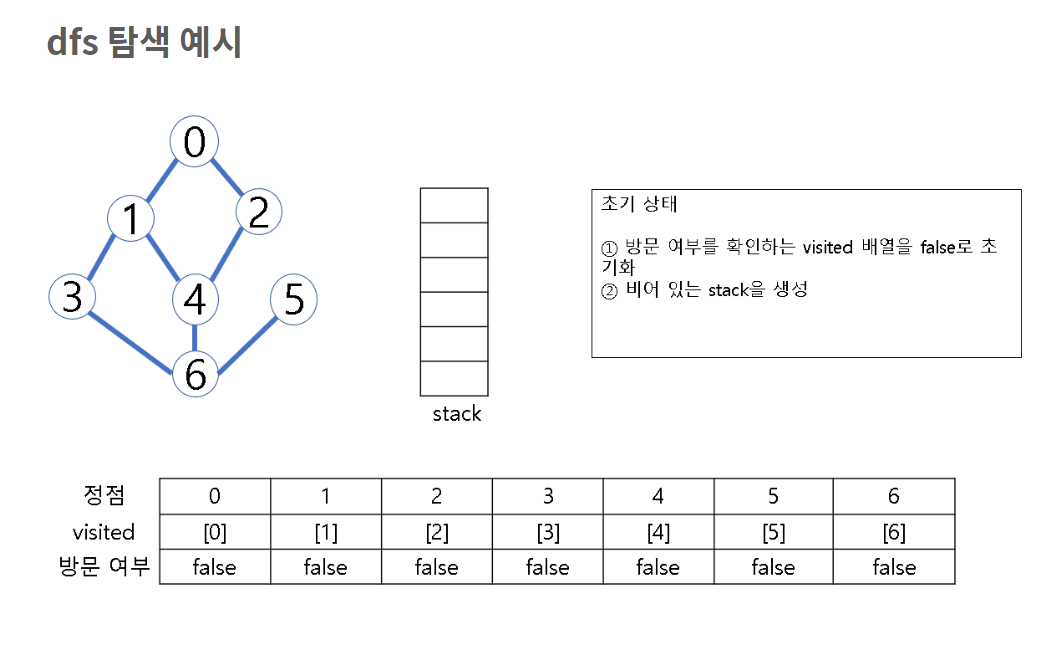
깊이 우선 탐색(DFS 탐색) & 스택

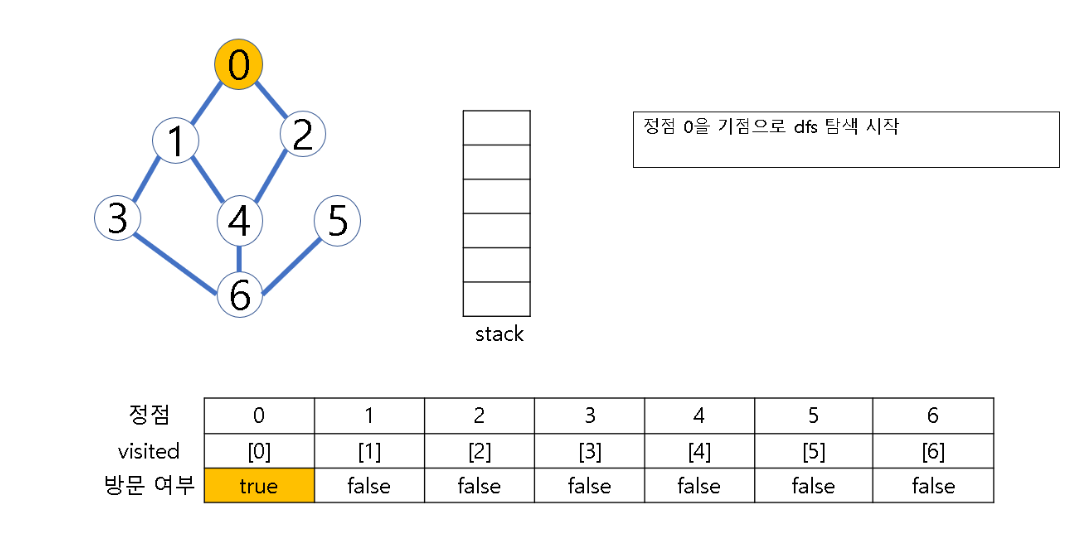
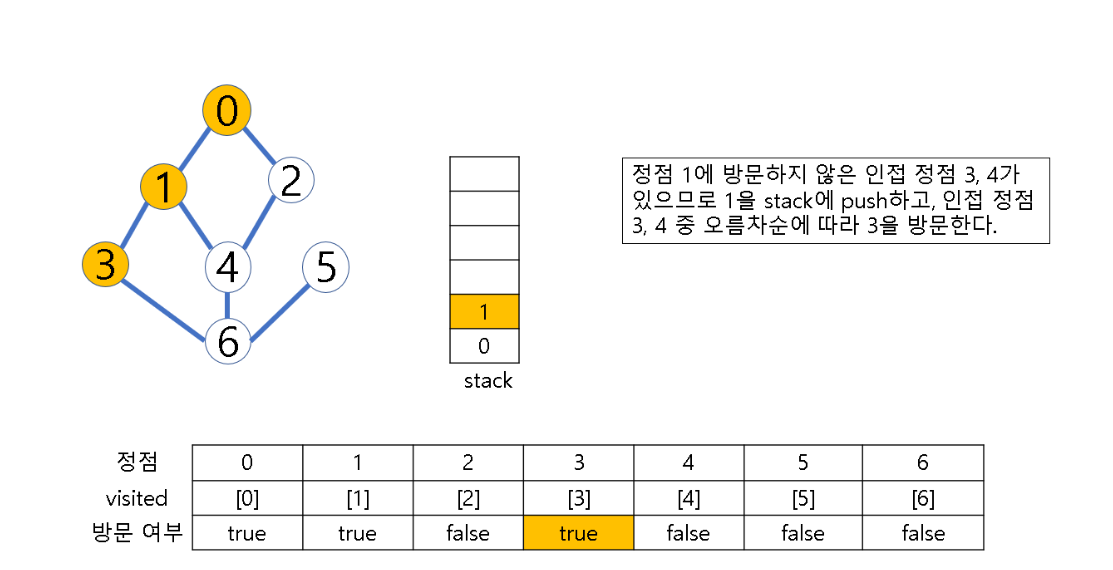
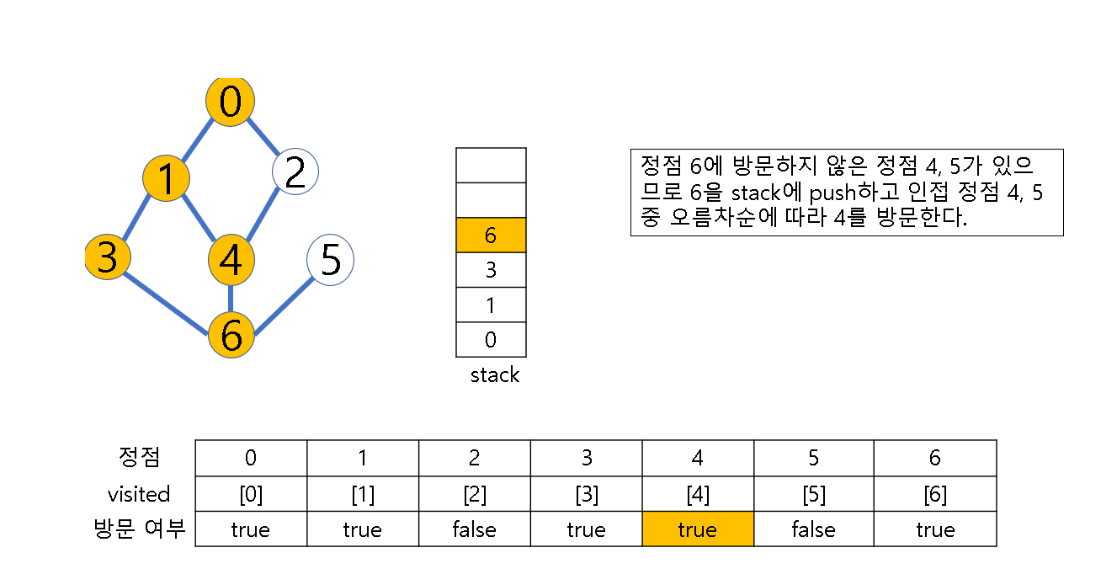
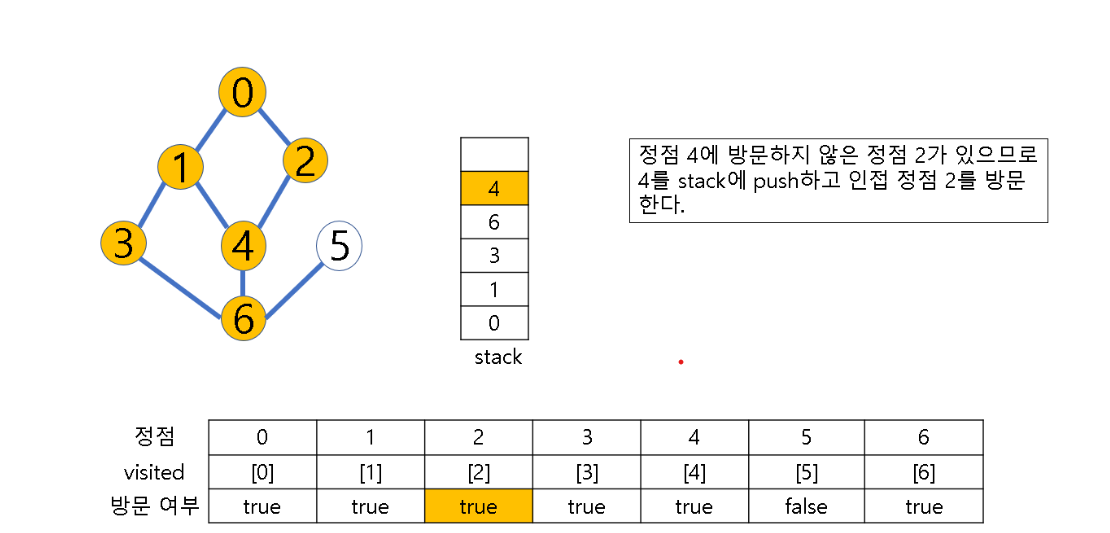
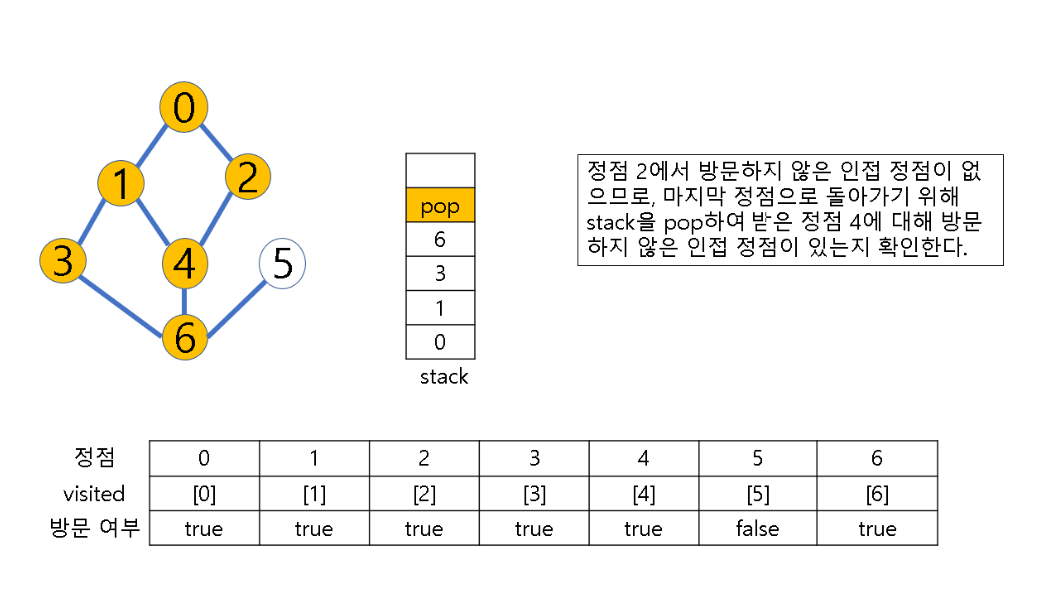
1. 시작 정점 v를 결정하여 방문
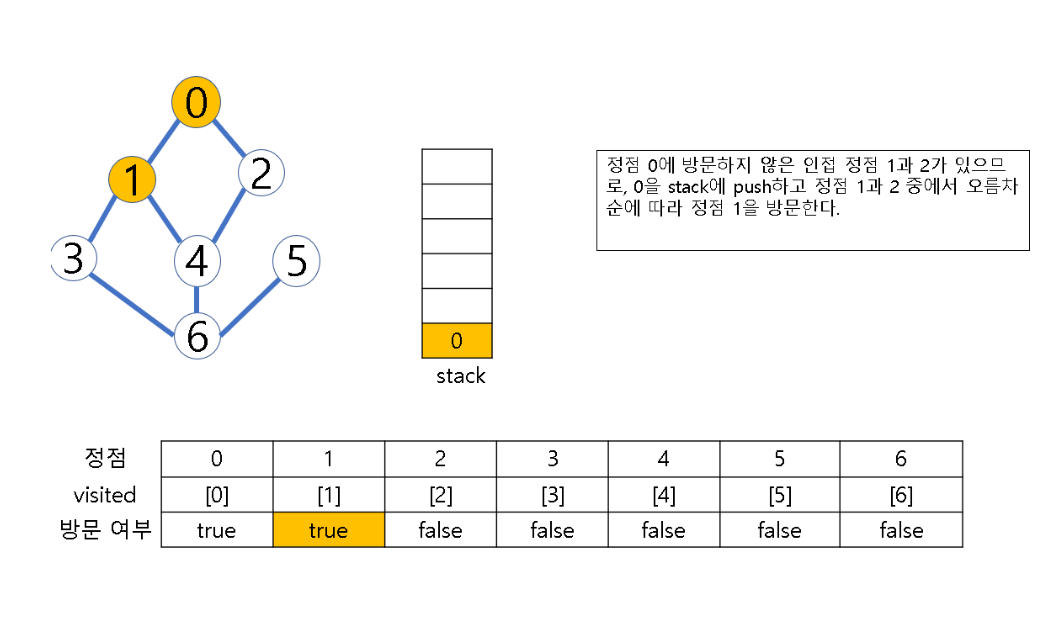
2. 정점 v에 인접한 정점 중에서
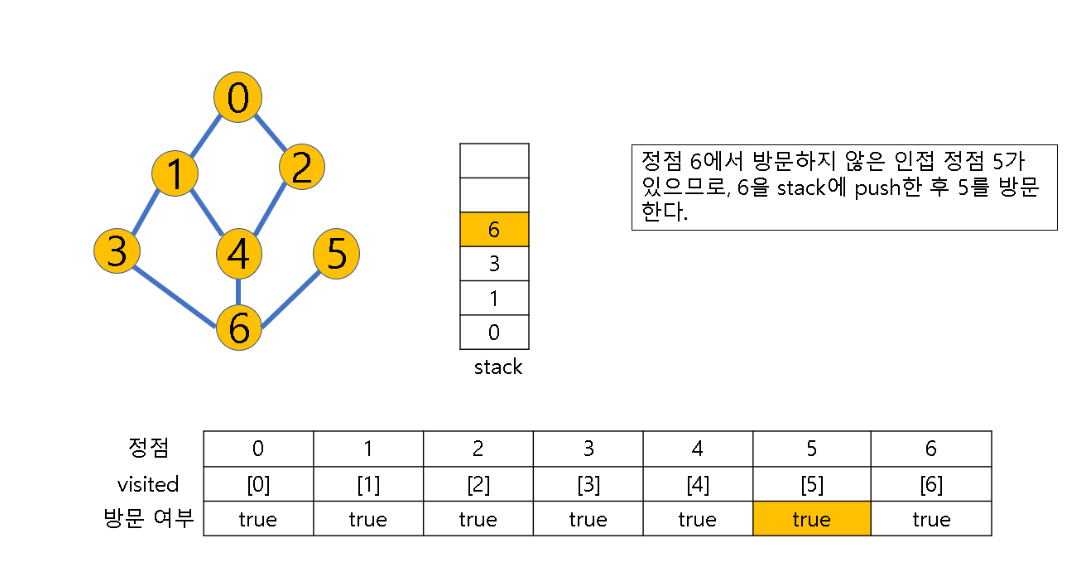
   (1) 방문하지 않은 정점 w가 있으면, 정점 v를 스택에 push하고 정점 w를 방문한다. 그리고 w를 v로 하여 다시 2번의 과정을 반복
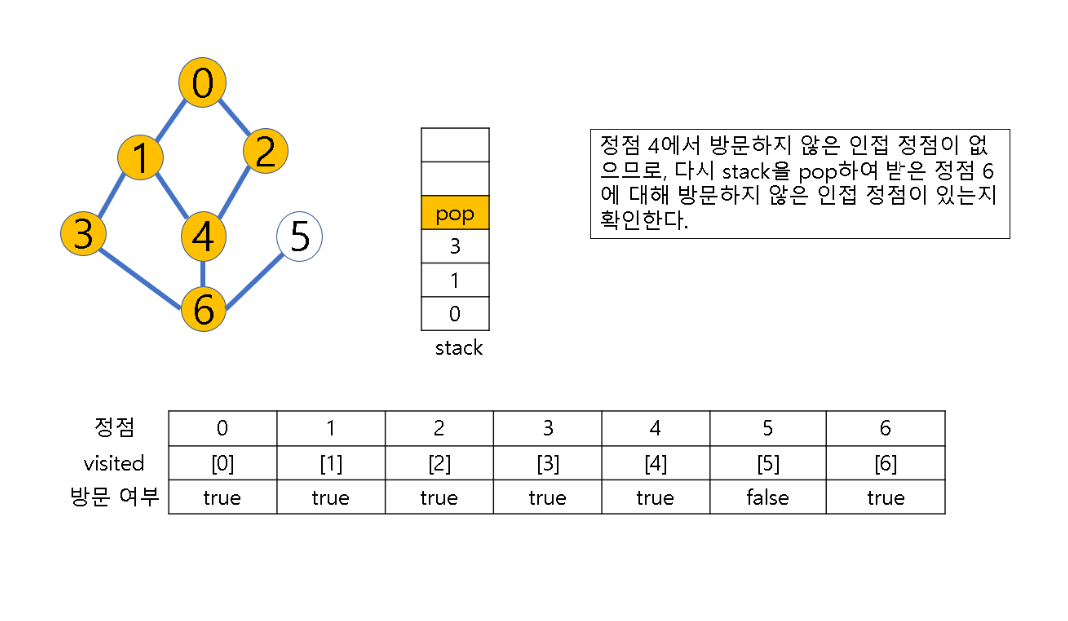
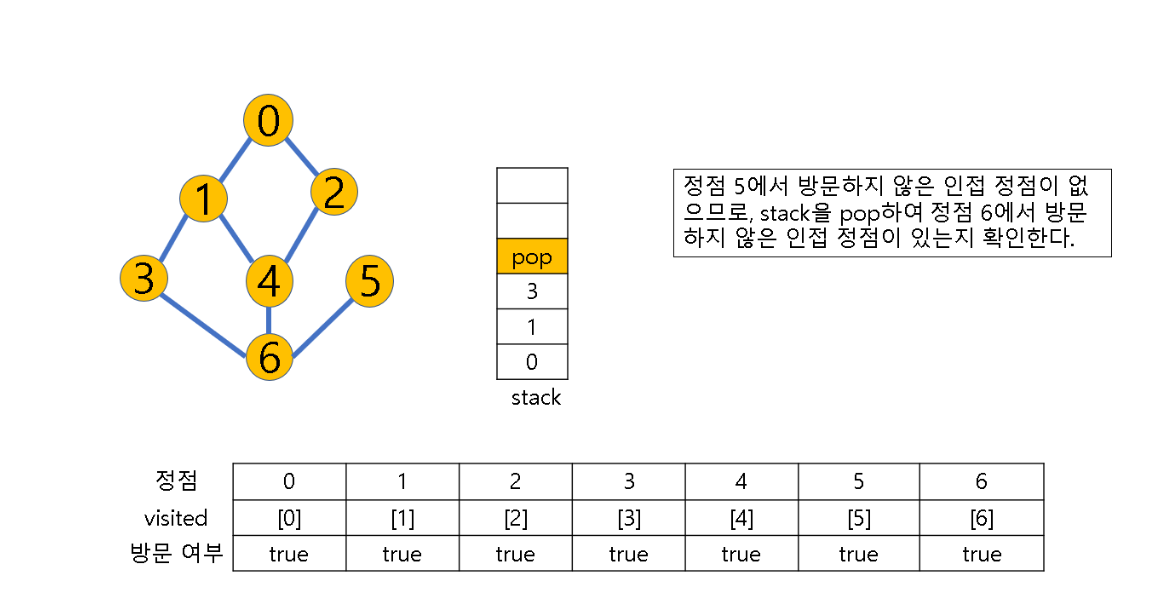
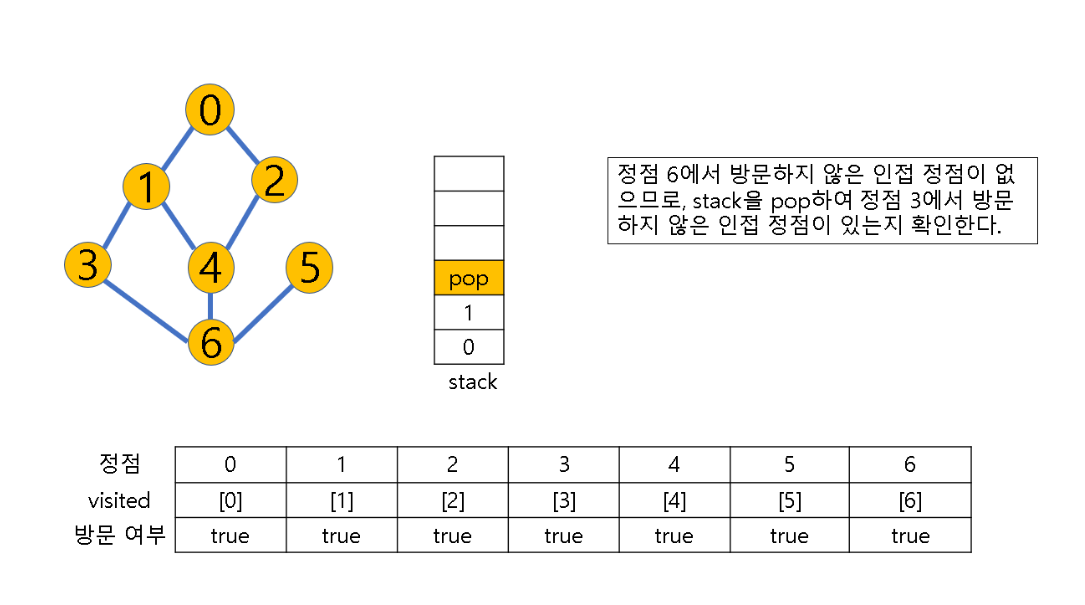
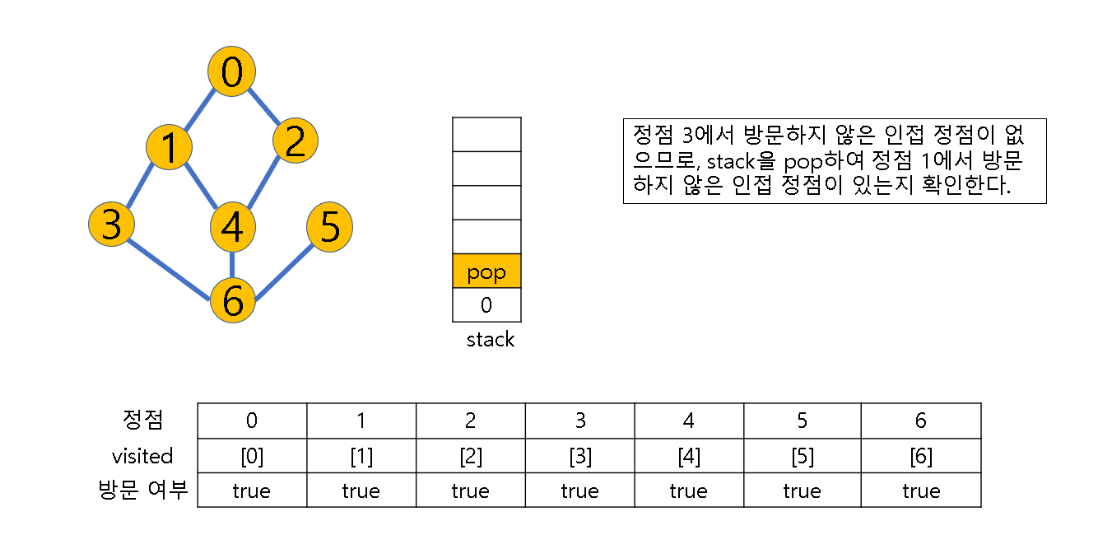
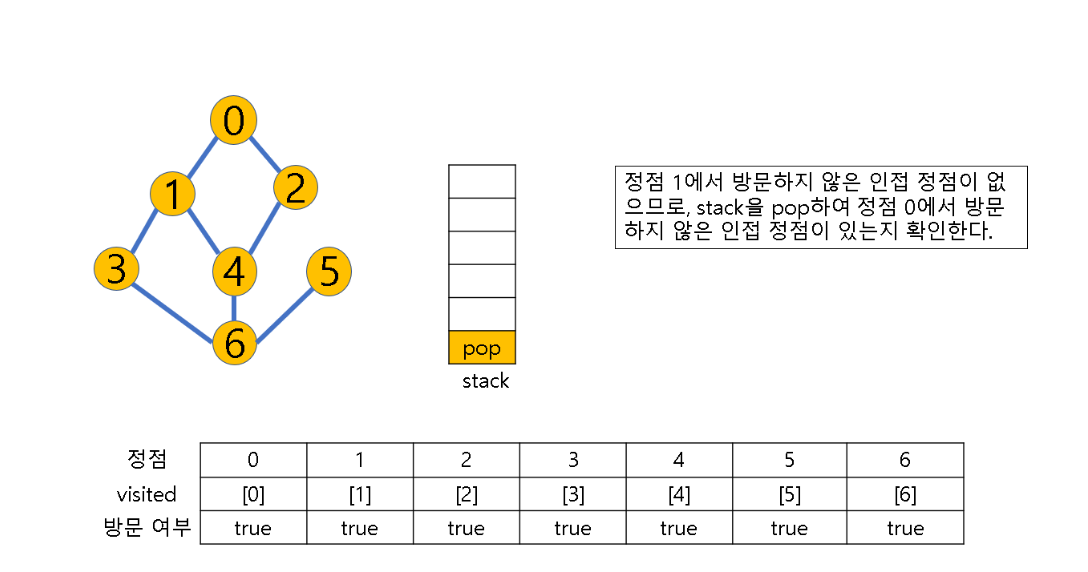
   (2) 방문하지 않은 정점이 없으면, 탐색의 방향을 바꾸기 위해 스택을 pop하여 받은 마지막 장문 정점을 v로 하여 다시 2번 과정을 반복
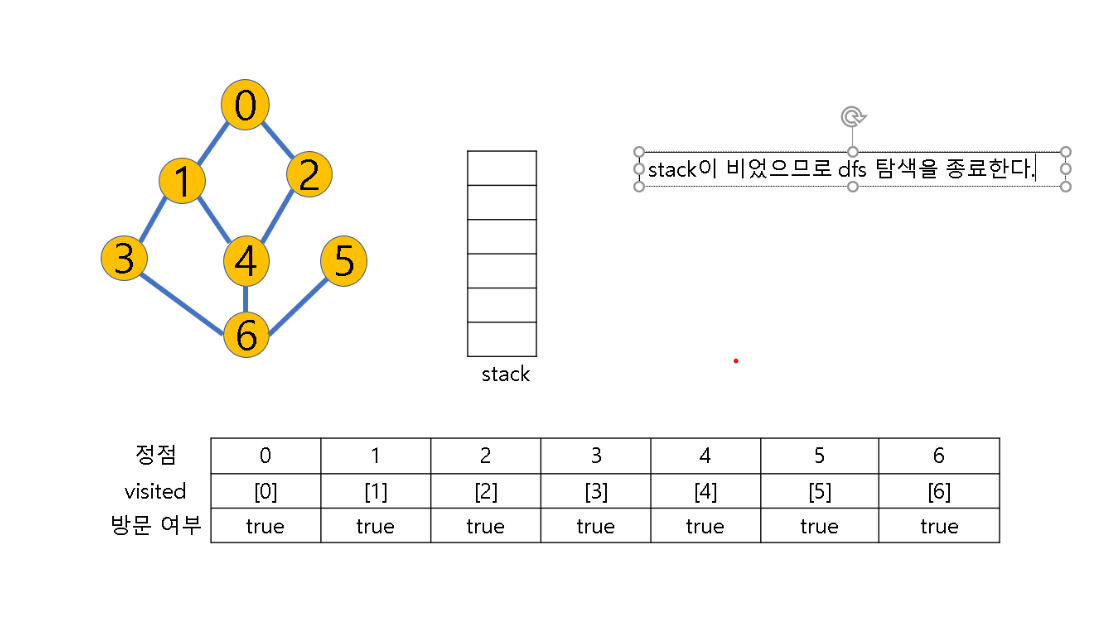
   (3) 스택이 공백이 될 때까지 2번 과정 반복

DFS 과정

<코드1>

void DFS(int v)
{
	node_pointer w;
	visited[v] = TURE;
	printf("%d", v);
	for (w = graph[v]; w; w = w->link)
	{
		if (!visited[w->vertex])
			DFS(w->vertex);
	}
}

🤷‍♂️ 전역 변수 visited[]를 false로 초기화한다. 해더 노드 배열은 graph[]이며, 각 노드에는 vertex 필드와 link 필드가 있다.

<코드2>

#include <stdio.h>
#include <memory.h>
#include <stdlib.h>
#include <stdbool.h>


#define MAX_VERTEX 10
#define FALSE 0
#define TURE 1



typedef struct GraphNode
{
	int vertex;
	struct GraphNode* link;
}GraphNode;


typedef struct GraphType
{
	int n;
	GraphNode* adjust_H[MAX_VERTEX];
	int visted[MAX_VERTEX];
}GraphType;

typedef struct StackNode
{
	int data;
	struct StackNode* link;

}StackNode;



StackNode* top;


void push(int item)
{
	StackNode* temp = (StackNode*)malloc(sizeof(StackNode));
	temp->data = item;
	temp->link = top;
	top = temp;
}


int pop()
{
	int item;
	StackNode* temp = top;

	if (top == NULL)
	{
		printf("\n\n Stack is empty ! \n");
		return 0;
	}

	else
	{
		item = temp->data;
		top = temp->link;
		free(temp);
		return item;
	}

}

void createGraph(GraphType* g)
{
	int v;
	g->n = 0;
	for (v = 0; v < MAX_VERTEX; v++)
	{
		g->visted[v] = FALSE;
		g->adjust_H[v] = NULL;
	}
}


void insertVertex(GraphType* g, int v)
{
	if ((g->n) + 1 > MAX_VERTEX)
	{
		printf("\n 그래프 정점의 개수를 초과하였습니다!");
		return;
	}

	g->n++;


}


void insertEdge(GraphType* g, int u, int v)
{
	GraphNode* node;
	if (u >= g->n || v >= g->n)
	{
		printf("\n 그래프에 없는 정점입니다.");
		return;

	}

	node = (GraphNode*)malloc(sizeof(GraphNode));

	node->vertex = v;
	node->link = g->adjust_H[u];

}


void printAdjList(GraphType* g)
{
	int i;
	GraphNode* p;

	for (i = 0; i < g->n; i++)
	{
		printf("\n\t\t정점%c의 인접리스트 ", i + 65);
		p = g->adjust_H[i];
	}

	while (p)
	{
		printf(" -> %c", p->vertex + 65);
		p = p->link;
	}

}

void dfsAdjList(GraphType* g, int v)
{
	GraphNode* w;
	top = NULL;
	push(v);
	g->visted[v] = TURE;
	printf("%c", v + 65);
	while (top != NULL)
	{
		w = g->adjust_H[v];
		while (w)
		{
			if (!g->visted[w->vertex])
			{
				push(w->vertex);
				g->visted[w->vertex] = TURE;
				printf("%c", w->vertex + 65);
				v = w->vertex;
				w = g->adjust_H[v];
			}
			else
			{
				w = w->link;
			}

			v = pop();
		}
	}

}


int main()
{
	int i;
	GraphType* G;
	G = (GraphType*)malloc(sizeof(GraphType));

	createGraph(G);

	for (i = 0; i < 6; i++)
	{
		insertVertex(G, i);
	}

	insertEdge(G, 0, 4);
	insertEdge(G, 0, 1);

	insertEdge(G, 1, 3);
	insertEdge(G, 1, 2);
	insertEdge(G, 1, 0);

	insertEdge(G, 2, 4);
	insertEdge(G, 2, 3);
	insertEdge(G, 2, 1);

	insertEdge(G, 3, 2);
	insertEdge(G, 3, 1);

	insertEdge(G, 4, 5);
	insertEdge(G, 4, 2);
	insertEdge(G, 4, 0);

	insertEdge(G, 5, 4);

	printf("%n G의 인접리스트 ");

	printAdjList(G);

	printf("\n\n 깊이우선탐색 >> ");
	dfsAdjList(G, 0);


	getchar();












}

DFS분석

인접 리스트로 구현했을경우

• DFS를 위해서 필요한 시간은 O(n+m)이다. 여기서 n은 정점 개수, m은 에지 개수이다.
• DFS가 총 N번 호출되긴 하지만 인접행렬과 달리 인접 리스트로 구현하게 되면 DFS 하나당 각 정점에 연결되어 있는 간선의 개수만큼 탐색을 하게 되므로 예측이 불가능하다.
• 하지만 DFS가 다 끝난 후를 생각하면 모든 정점을 한번씩 다 방문하고, 모든 간선을 한번씩 모두 검사했다고 할 수 있으므로 O(n+m)의 시간이 걸렸다고 할 수 있다.

인접 행렬로 구현했을경우

• 시간복잡도는 DFS 하나당 N번의 loop를 돌게 되므로 O(n)의 시간복잡도를 가진다. 그런데 N개의 정점을 모두 방문해야하므로 n * O(n) = O(n^2)의 시간복잡도를 가진다.

출처

https://currygamedev.tistory.com/10
https://wookkingkim.tistory.com/32