이번 시간에는 이진탐색에 대해서 알아보겠다.
이 알고리즘을 적용시키는데 전제 조건은 데이터가 키 값으로 이미 정렬 되어 있어야 한다.
이진탐색
- 오름차순 OR 내림차순으로 정렬된 배열에서 검색하는 방법이다.
<그림 출처| https://medium.com/quantum-ant/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-13%EC%9E%A5-%ED%83%90%EC%83%89-cbd7cbf7155d>
-
n개의 요소가 오름차순으로 늘어선 배열 a에서 키를 이진 탐색으로 검색하는 과정을 일반화하면,
- 맨 앞 인덱스 pl
- 중앙 인덱스 pc라고 지정한다.
- 맨 끝 인덱스 pr
-
검색을 시작할 떄, pl = 0 // pc = (n-1)/2 // pr = n-1로 설정한다.
-
a[pc](검사할 요소)와 key를 비교하여 검색 범위를 나눌 수 있다.
-
a[pc] < key
- a[pl] ~ a[pc]는 key보다 작기 때문에 검색 대상에서 제외시킨다.
- 검색 범위는 a[pc+1] ~ a[pr]로 좁혀진다.
- 마지막으로 pl의 값을 pc + 1로 업데이트한다.
-
a[pc] > key
- a[pc] ~ a[pr]은 key보다 크기 때문에 검색 대상에서 제외한다.
- a[pl] ~ a[pc-1]로 좁혀진다. pr값을 pc-1로 업데이트한다.
-
-
이진 검색 알고리즘의 종료조건을 이와같이 정리할 수 있다.
1. a[pc]와 key가 일치하는 경우
2. 검색 범위가 더 이상 없는 경우-
이진 탐색은 검색을 반복할 떄마다 검색 범위가 절반이 되므로 검색에 필요한 비교 횟수의 평균값은 log n이다.
- 검색에 실패한 경우는 [log(n+1)]회,
- 검색에 성공한 경우는 log[n-1]회다.
- 이진탐색은 검색 대상이 정렬 되어 있다는 것을 잊지말자.(가정)
※[ ] 함수 (ceiling function) 천장함수
- [ x ]는 x의 천장함수이며, x보다 크거나 같으면서 가장 작은 정수다.
- [3.5] = 4다. 올림 함수로 보면 된다.
다음 예제를 보자.
#include <stdio.h>
#include <stdlib.h>
int bin_search(const int a[], int n, int key)
{
int pl = 0; //검색 맨 앞의 인덱스
int pr = n - 1; // 검색 맨 끝 인덱스
int pc; // 검색 범위 한 가운데 인덱스
do {
pc = (pl + pr) / 2;
if (a[pc] == key)
return pc;
else if (a[pc] < key)
pl = pc + 1;
else
pr = pc - 1;
} while (pl <= pr);
return -1;
}
int main()
{
int i, nx, ky, idx = 0;
int* x; //배열의 첫 번째 요소에 대한 포인터 생성
puts("이진 검색 : ");
printf("요소 개수 : ");
scanf_s("%d", &nx);
x = calloc(nx, sizeof(int));
printf("오름차순으로 입력하세요 : \n");
printf(" x[0] : ");
scanf_s("%d", &x[0]);
for (i = 1; i < nx; i++)
{
do {
printf("x[%d] : ", i);
scanf_s("%d", &x[i]);
} while (x[i] < x[i - 1]); //바로 앞의 값보다 작으면 다시 입력한다.
}
printf("검색값 : ");
scanf_s("%d", &ky);
idx = bin_search(x, nx, ky); //배열 x에서 값이 ky인 요소를 이진검색한다.
if (idx == -1)
{
puts("검색에 실패했습니다.");
}
else
{
printf("%d는 x[%d]에 있습니다 \n", ky, idx);
}
free(x);
return 0;
}
<결과>
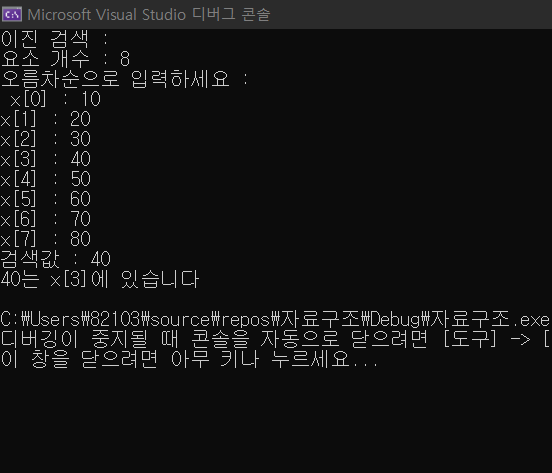
핵심코드 <1>
int bin_search(const int a[], int n, int key)
{
int pl = 0; //검색 맨 앞의 인덱스
int pr = n - 1; // 검색 맨 끝 인덱스
int pc; // 검색 범위 한 가운데 인덱스
do {
pc = (pl + pr) / 2; // pc는 pl+pr/2로 구성된다. == n-1/2
if (a[pc] == key) // a[pc] == key와 같으면 원하는 값을 찾은 것.
return pc;
else if (a[pc] < key)
// 다른 경우의 수 a[pc] < key이다.
// key보다 작다는 의미는 pl~pc까지의 범위가 필요 없다는 의미
pl = pc + 1;
else
//(a[pc] > key)로 구성된다.
pr = pc - 1;
} while (pl <= pr); // pl과 pr이 같거나 클 때까지 반복한다.
return -1;
}핵심코드 <2>
// 이 부분은 사용자가 콘솔창에 입력할 때, 오름차순 기준으로 정렬해야 되기 떄문에 조건을 걸었다.
for (i = 1; i < nx; i++)
{
do {
printf("x[%d] : ", i);
scanf_s("%d", &x[i]);
} while (x[i] < x[i - 1]); //바로 앞의 값보다 작으면 다시 입력한다.
}프로그램의 실행 속도는 하드웨어나 컴파일러 등의 조건에 따라 달라진다.
알고리즘의 성능을 객관적으로 평가하는 기준을 복잡도라고 한다.
1. 시간 복잡도(time complexity) : 실행에 필요한 시간을 평가한 것.
2. 공간 복잡도 (space complexity) : 기억 영역과 파일 공간이 얼마나 필요한가를 평가한 것.다음 예제는 선형 검색의 시간 복잡도 예제다.
int Search(const int a[], int n, int key)
{
int i = 0; //변수 i에 0를 대입 하는 횟수는 처음 한 번 실행한 이후에는 없다.
// 한 번만 실행되기 때문에 O(1)
while(i < n)// 배열의 맨 끝에 도달했는지를 판단하고,
{
if(a[n] == key) // 요소와 찾고자 하는 값이 같은지를 판단하는 평균 실핼 횟수는 n/2다.
return i; // 한 번만 실행되기 때문에 O(1)
i++;
}
return -1; //한 번만 실행되기 때문에 O(1)
}- 복잡도 n/2과 N의 차이는 크지 않다.
- n/2번 실행 했을 때, O(n/2)가 아닌 O(n)로 쓰는 이유는 n의 값이 무한히 커진다고 가정 했을 때, 값의 차이가 무의미해진다.
- 100번만 실행하는 경우 O(100)이 아닌 O(1)로 표기한다. 그만큼 사람이 느끼는 차이는 적다.
<복잡도 정리>
int i = 0; ---> 실행 횟수 : 1 복잡도 : O(1)
while(i < n) ----> 실행 횟수 : n/2 복잡도 : O(n)
{
if(a[n] == key) ---> 실행 횟수 : n/2 복잡도 : O(n)
return i; ---> 실행 횟수 : 1 복잡도 : O(1)
i++; ----> 실행 횟수 : n/2 복잡도 : O(n)
}
return -1; ---> 실행 횟수 : 1 복잡도 : O(1)
}
일반적으로 n이 점점 커지면 O(n)에 필요한 계산 시간은 n에 비례하여 길어진다.
O((fn))과 O((gn))의 복잡도를 계산하는 방법은 이와같다.
O((fn)) + O((gn)) = O(max(f(n), g(n));
※여기서 max 함수는 a ,b 가운데 큰 값을 나타내는 함수다.
위 식을 계산하면,
O(1) + O(n) + O(n) + O(1) + O(n) + O(1) = O(max(1,n,n,1,n,1)) = O(n)- 복잡도 정리
다음은 이진 검색의 시간 복잡도를 살펴보자.
int bin_search(const int a[], int n, int key)
{
int pl = 0; //실행 횟수 : 1 | 복잡도 : O(1)
int pr = n - 1; //실행 횟수 : 1 | 복잡도 : O(1)
do{
int pc (pl + pc) / 2; //실행 횟수 : log n | 복잡도 : O(log n)
if(a[pc] == key) //실행 횟수 : log n | 복잡도 : O(log n)
return pc; //실행 횟수 : 1 | 복잡도 : O(1)
else if(a[pc] < key) //실행 횟수 : log n | 복잡도 : O(log n)
pl = pc + 1; //실행 횟수 : log n| 복잡도 : O(log n)
else //실행 횟수 : log n| 복잡도 : O(log n)
pr = pc - 1; //실행 횟수 : log n| 복잡도 : O(log n)
}while(pl <= pr); //실행 횟수 : log n| 복잡도 : O(log n)
return -1; //실행 횟수 : 1 복잡도 : O(1)
}
식으로 나타내면, O(1) + O(1) + O(log n) + O(log n) + O(1) + O(log n) + O(1) = O(log n)
아는만큼보인다.